Comprehensive reliability evaluation of foreign high-end gantry machining Center

Wen-kai NI, Feng-bo YU, Ji-qiang WEI, Cheng-dao PIAO,3*

(1College of Engineering, Yanbian University, Yanji 133002, China)(2College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China)(3Engineering Training Center, Yanbian University, Yanji 133002, China)



Comprehensive reliability evaluation of foreign high-end gantry machining Center

Wen-kai NI1, Feng-bo YU2, Ji-qiang WEI1, Cheng-dao PIAO1,3*

(1CollegeofEngineering,YanbianUniversity,Yanji133002,China)(2CollegeofMechanicalandElectricalEngineering,ChinaJiliangUniversity,Hangzhou310018,China)(3EngineeringTrainingCenter,YanbianUniversity,Yanji133002,China)

The time between failures, two groups of failure data of foreign high-end gantry machining center, were collected by failure truncated testing. MTTFF and MTBF in different truncated number were calculated by the traditional method of reliability analysis. Then, the weights of MTTFF and MTBF of different samples were determined by dynamic weighting method. Eventually, the evaluated systems were sorted by Borda count function. The results show that A2group is significantly better than A1group. And the dynamic weighting method in multiple failure truncated testing could fully reflect the difference of the evaluated object both in the quality and quantity, which is a feasible method for reliability evaluation of gantry machining center.

Failure truncated testing, Dynamic weighting method, Mean time to first failure, Gantry machining center

1 Introduction

Gantry machining center refers to the vertical setting of the spindle axis and the work table of machining center, which is suitable for machining various kinds of basic parts, plate, shell parts, mold, etc [1]. It is applied widely in manufacturing industry, because it can complete a variety of processes such as milling, drilling, boring, reaming, tapping, etc. with automatic, efficient and high precision at one time clamping [2]. Although gantry machining center has high processing efficiency, it cannot avoid the occurrence of failure which results economic losses [3]. Therefore, it is necessary to study the reliability of the gantry machining center in order to enhance its reliability.

Many scholars studied on the NC machine tool reliability evaluation [4-8], but rarely involved failure truncated testing. Failure truncated testing is also called type Ⅱ censoring test, the testing is terminated after a truncated number of failures,r, has occurred. And the test time is then given bytr, the failure time of therth failure [9]. TypeⅡcensoring test could bring certain value of the research in CNC machine tool and reliability index, but there is not yet a well evaluation criteria for the truncated number. If the selected truncated number is not good, it will make the machine reliability analysis and evaluation inaccurate. A new method can effectively and objectively evaluate the similar model and even different classes of CNC machine tools, which can better avoid this situation. Taking the SIRIUS-1250 gantry machining center as an example, this method was introduced by a company in South Korea. As shown in Fig.1, this gantry machining center configuration of CNC system is FANUC-18iMB, with 40 cutters in cutter storehouse and the characteristics of high-speed processing, heavy cutting, processing range etc.

2 Calculation of reliability index

The fault information of 29 sets of SIRIUS-1250 gantry machining center with 2 groups (recorded as A1group and A2group) was collected, the machine tool number of A1group was G01-G15 and A2group of machine tool number was G16-G29. Table 1 recorded the data of time between failures of the SIRIUS-1250 gantry machining center in accordance with the judgment rules of fault data and the principle of fault counting by professional, which used data collection method with type Ⅱ censoring test. In the process of data collection, the data that cannot reflect the fault information of the gantry machining center can be eliminated, which could ensure the data’s authenticity and validity.

In the typeⅡcensoring test, the truncated numberrtook 6-10, respectively, for each processing center. Thereby two evaluation systems were constituted, which was noted for {A1r}, {A2r} (r=6, 7, 8, 9, 10).

Fig.1SIRIUS-1250gantrymachiningcenter

Table 1 Time between failures of SIRIUS-1250 gantry machining center

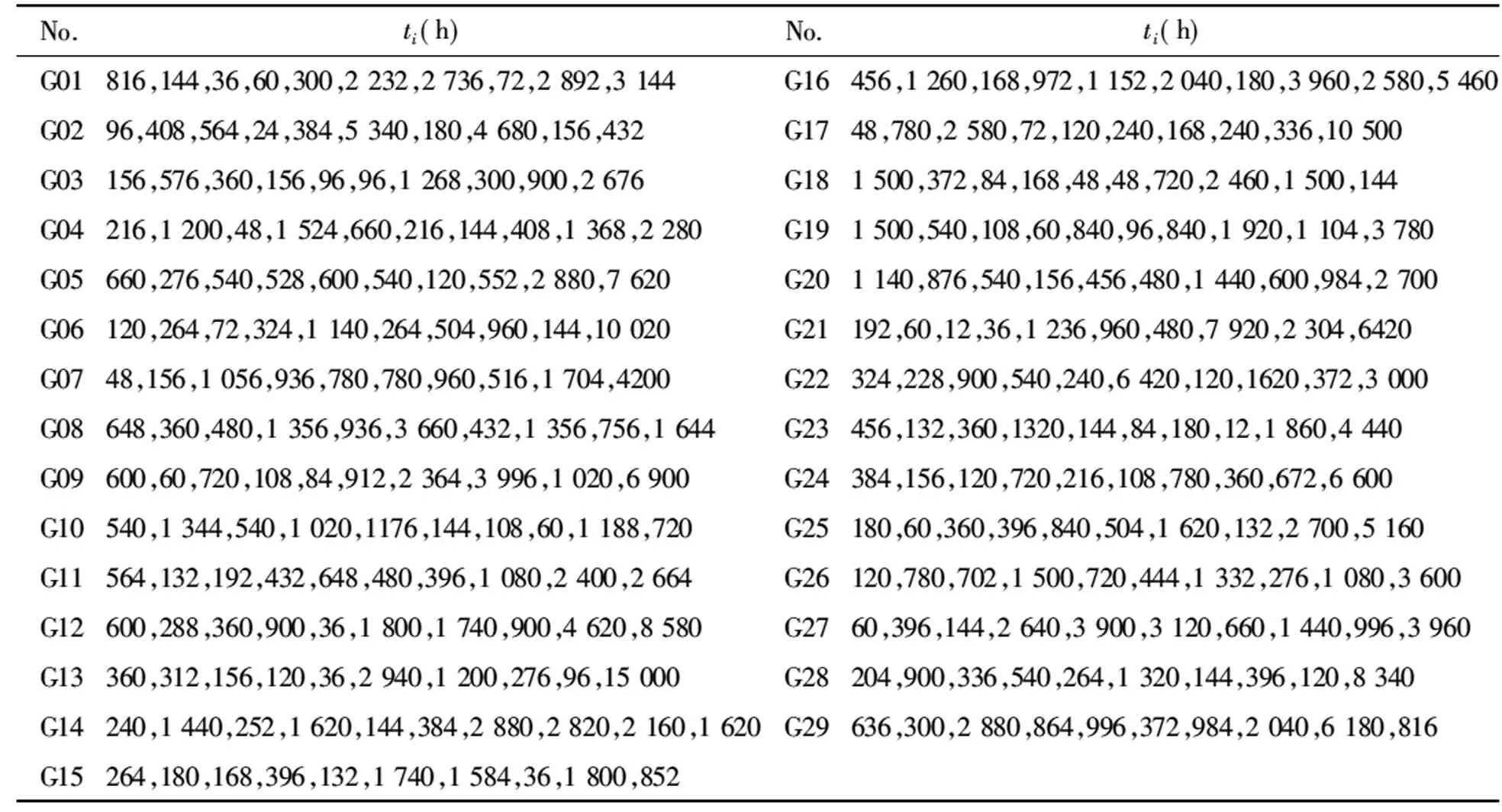
No.ti(h)No.ti(h)G01816,144,36,60,300,2232,2736,72,2892,3144G16456,1260,168,972,1152,2040,180,3960,2580,5460G0296,408,564,24,384,5340,180,4680,156,432G1748,780,2580,72,120,240,168,240,336,10500G03156,576,360,156,96,96,1268,300,900,2676G181500,372,84,168,48,48,720,2460,1500,144G04216,1200,48,1524,660,216,144,408,1368,2280G191500,540,108,60,840,96,840,1920,1104,3780G05660,276,540,528,600,540,120,552,2880,7620G201140,876,540,156,456,480,1440,600,984,2700G06120,264,72,324,1140,264,504,960,144,10020G21192,60,12,36,1236,960,480,7920,2304,6420G0748,156,1056,936,780,780,960,516,1704,4200G22324,228,900,540,240,6420,120,1620,372,3000G08648,360,480,1356,936,3660,432,1356,756,1644G23456,132,360,1320,144,84,180,12,1860,4440G09600,60,720,108,84,912,2364,3996,1020,6900G24384,156,120,720,216,108,780,360,672,6600G10540,1344,540,1020,1176,144,108,60,1188,720G25180,60,360,396,840,504,1620,132,2700,5160G11564,132,192,432,648,480,396,1080,2400,2664G26120,780,702,1500,720,444,1332,276,1080,3600G12600,288,360,900,36,1800,1740,900,4620,8580G2760,396,144,2640,3900,3120,660,1440,996,3960G13360,312,156,120,36,2940,1200,276,96,15000G28204,900,336,540,264,1320,144,396,120,8340G14240,1440,252,1620,144,384,2880,2820,2160,1620G29636,300,2880,864,996,372,984,2040,6180,816G15264,180,168,396,132,1740,1584,36,1800,852

2.1 Mean time to first failures

The mean time to first failures (MTTFF) is the cumulative average working time of the first failure of devices or components after they are under operation, it is a reliable characteristic to describe the maintenance system for the first fault status [10]. Obviously, MTTFF has no correlation with truncated number.

The fault distributions of the CNC machine tools include normal distribution, logarithmic normal distribution, exponential distribution and weibull distribution [8]. First of all, the first failure time of gantry machining center was assumed that it obeys the above of distributions; secondly, the parameters of these four distributions were respectively estimated by maximum likelihood estimator method; finally, the parameters of these four distributions were inspected by Kolmogorov-Smirnov test method. The analysis results of A1group and A2group were showed in Table 2 and Table 3, respectively. In these tables, if the inspection result value,H, is “0”, it means failure data obeys the distribution to be tested, otherwise, a value of “0” means that the failure data disobeys the tested distribution; Obedience probability, P, reflects the accurate degree for the data obeying to distribution test, the value is greater it is more likely to obey a certain tested distribution.

As Table 2 showed, the first failure time of A1group obeyed the above four kinds of distributions. The time to first failure, because the obedience probability P of normal distribution was higher than the others, was judged to obey normal distribution, and the value of MTTFF was calculated by point estimate method:MTTFF=E(t)=395.20 hour. Simultaneously, the time to first failure of A2group was judged to obey lognormal distribution as Table 3 showed, and the value of MTTFF was calculated by point estimate method:MTTFF=E(t)= 547.26 hour.

Table 2 Parameter estimation and parameter test of A1group in the specified distribution

DistributiontypeParameter1Parameter2HPNormal395.20239.7400.5618Lognormal5.71210.818600.3653Exponential395.20—00.4512Weibull440.761.636000.4113

Table 3 Parameter estimation and parameter test of A2group in the specified distribution

DistributiontypeParameter1Parameter2HPNormal514.29485.5600.2449Lognormal5.75851.045400.9941Exponential514.29—00.9582Weibull529.501.073600.9075

2.2 Mean time between failures

Mean time between failures (MTBF) is the predicted elapsed time between inherent failures of a system during operation [11].

The analytical calculation of time between failures was similar to the method of analyzing the first failure time. Firstly, the mean time between failures of gantry machining center was assumed that it obeys the above distributions; secondly, the parameters of these four distributions were estimated by maximum likelihood estimator method, respectively; thirdly, the parameters of these four distributions were inspected by Kolmogorov-Smirnov test; fourthly, the fault data was judged to obey what kind of distribution by obedience probability; finally, the MTBF value was calculated by point estimate method. The analysis results of different evaluation systems were shown in Table 4.

Table 4 Analytical calculation of the MTBF

EvaluationsystemDistributionofsubjectParameter1Parameter2MTBFA1A16Lognormal5.86941.1207663.40A17Lognormal5.95931.1434744.70A18Lognormal6.00111.1873817.25A19Lognormal6.10481.2179940.53A110Lognormal6.29271.32411299.00A2A26Lognormal5.90981.2203776.17A27Weibull684.710.91440714.33A28Lognormal6.02431.2600914.25A29Weibull852.430.8660916.89A210Lognormal6.33081.38361462.60

It is noticed that MTBF ofA2group was higher than MTBF ofA1group when the truncated numberr=6, 8, 10, whiler=5, 7, MTBF ofA1group was higher than MTBF ofA2group.

3 Reliability comprehensive evaluation based on dynamic weighting method features

Dynamic weighting method to solve the problem was divided into three steps. First of all, the evaluation indexes were standardized. Then, according to the characteristics of evaluation index, the dynamic weighting function was selected. Last but not the least, comprehensive evaluation model was constructed [12-14].

3.1 Standardization of evaluation index

Based on national science and technology major project and expert experience, the reliability index is divided into 5 grades [8], the range of the reliability index was shown in Table 5.

Table 5 The range of the reliability index

GradeEvaluationindexMTTFF/hMTBF/hVeryhigh>1500>1800High[1000,1500)[1200,1800)intermediate[700,1000)[800,1200)Low[500,700)[600,800)Verylow[300,500)[400,600)

It is noticed that both MTTFF and MTBF were the partial larger index. First of all, the minimization of MTTFF was done by reciprocal transformation, and the corresponding classification standard interval was (0, 1/15], (1/15, 1/10], (1/10, 1/7], (1/7, 1/5], (1/5, 1/3]. Then, the data was standardized by range transform, and the corresponding classification interval was (0, 0.2], (0.2, 0.3], (0.3, 0.43], (0.43, 0.6], (0.6, 1].

In the same way, the range of MTBF was standardized, and the corresponding classification interval is (0, 0.22], (0.22, 0.33], (0.33, 0.5], (0.5, 0.67], (0.67, 1].

Letxkijis the standardized value of evaluation indexiby failure truncated testingj(equal to truncated numberrminus 5, that isj=r-5) in evaluation systemk. Due to reciprocal transformation in the standardization processing, the evaluation index,xkij, is smaller, which means that the evaluation index is better.

3.2 Selection of dynamic weighting function

Taking into account the difference of the evaluation index in the quality and quantity, the comprehensive evaluation index not only reflects the differences between different types of indicators, but also reflects the same type of indicators in quantity. Thus, the dynamic weighting functionωi(xkij) was selected for partial larger normal distribution function based on the characteristics ofMTTFF(i=1) andMTBF(i=2) index. The dynamic weighting function is as follows:

(1)

3.3 Comprehensive reliability evaluation

Accordingtothestandardprocedureoftheevaluationindexxkijandthecorrespondingdynamicweightingfunctionωi(xkij),thecomprehensivereliabilityevaluationmodelforA1groupandA2groupcouldbeestablished.ThecomprehensiveevaluationindexfunctionYkjwastakenasthedynamicweightingsumofeachevaluationindex.Set

(2)

Formula (2) is the comprehensive evaluation index function, there have five sample observation values (5 truncated number) for A1group (k=1) and A2group (k=2). Thus, the comprehensive evaluation model (Ykj)2×5was 2×5 order matrix. Then

The comprehensive ranking scheme could be determined by the Borda count function method [15] in decision analysis. NotesBj(Akr) as the number that behind the No.kevaluated objectAkrin the ranking schemej(j=r-5), and Borda count is

(3)

Therefore, the comprehensive evaluation model (Ykj)2×5could be stored by column with its size, the five sorted schemes could be obtained. The comprehensive evaluation results of the two subjects were calculated,B(A1)=5,B(A2)=0. The results showed that the reliability of A2group was significantly better than that of A1group.

4 Summary

The reliability evaluation index’s weight of gantry machining center was established by dynamic weighting method, it could avoid the evaluation defects for the inappropriate truncated number. From the actual comprehensive evaluation results, it could be seen that dynamic weighting method is scientific and reasonable for such a class of multi factor and multi attributes which contains both the difference of quality and quantity. Obviously, it is a feasible method to evaluate the reliability of gantry machining center based on the objective and dynamic weighted of the index data which provided by the manufacturer. According to the actual situation, the evaluation index could be adjusted, which makes the evaluation results more realistic.

[1]Zhang Dinghua. Handbook of numerical control machining first volume[M]. Beijing: Chemical industry press, 2013:273-307.

[2]Yu K T, Sheu S H, Chen K S. The evaluation of process capability for a machining center[J].The International Journal of Advanced Manufacturing Technology, 2007, 33: 505-510.

[3]Peter F. McGoldrick, Kulluk H. Machine Tool Reliability—A Critical Factor in Manufacturing Systems[J]. Reliability Engineering, 1986(14): 205-221.

[4]SHEN Guixiang, ZHANG Yingzhi, XUE Yuxia. Comprehensive evaluation on reliability of numerically- controlled machine tool based on entropy weight method [J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(5): 1208-1211.

[5]LIU Yongjun, FAN Jinwei, LI Yun. Reliability evaluation method and algorithm for electromechanical product[J].Journal of Central South University. 2014(10): 3753-3761.

[6]ZHANG Hongbin, JIA Zhixin, XIAN Min. Reliability Evaluation of DK77 Series WEDM Based on Fuzzy Comprehensive Evaluation[J]. Machine Tool & Hydraulics, 2009, 37(11): 246-247.

[7]LI Huiliang, JIA Xianzhao, ZHANG Tao. Reliability Analysis of NC Machine Tools Based on Weibull Distribution[J].Machine Tool & Hydraulics, 2014, 42(19):191-194.

[8]Liu Kuo, Liu Chunshi, Lin Jianfeng. Research on CNC Machine Tools failure Distribution model and reliability Evaluation Technology[J]. Machine Tool & Hydraulics, 2012, 40(15):148-150.

[9]Ebeling C E. An Introduction to Reliability and Maintainability Engineering[M]. Illinois: Waveland Press, 2005.

[10]AOChangLin, QIAO Jinyou, DAI Youzhong. Statistical analysis of the field credibility test under the situation of weibull process[J]. Journal of Northeast Agricultural University, 2000, 31(3):303-306.

[11]Jones, James V. Integrated Logistics Support Handbook, 3rd edition[M]. [S.l.]: McGraw-Hill Professional, 2006.

[12]Han Zhonggen. The mathematical model of water quality comprehensive evaluation and prediction of the Yangtze river [J]. Chinese Journal of Engineering Mathematics, 2005, 22(7): 65-72.

[13]Sun Liang, Han Chongzhao. Dynamic weighted voting for multiple classifier fusion: a generalized rough set method [J]. Journal of Systems Engineering and Electronics, 2006, 17(3): 487-494.

[14]ZHU Wenxing, Yan Yuanhui. Solving the weighted MAX-SAT problem using the dynamic convexized method [J]. Optimization letters, 2014, 8(1): 359-374.

[15]YUE Chaoyuan. Decision Theory and method [M]. Beijing: Science Press, 2012.

10.3969/j.issn.1001-3881.2015.24.005 Document code: A

TG659

国外高档龙门式加工中心的可靠性综合评价

倪文凯1，于丰博2，隗纪强1，朴成道1,3*

1.延边大学 工学院， 吉林 延吉133002 2.中国计量学院 机电工程学院， 杭州310018 3.延边大学 工程训练中心， 吉林 延吉133002

采用定时截尾试验法收集了2组国外高档龙门式加工中心的故障数据。通过传统的可靠性分析方法分别计算了不同截尾次数下的MTBF和MTTFF，然后通过动态加权法确定了不同样本下的MTTFF与MTBF的权重，最后通过波达计数函数对这两组机床进行了排序。结果表明： A2组明显好于A1组，同时也表明多次截尾实验下的动态加权法充分体现了评价对象的“质差”和“量差”，是一种切实可行的数控机床可靠性评价方法。

定数截尾实验；动态加权法；平均首次故障时间；龙门式加工中心

14 July 2015; revised 16 October 2015;

Cheng-dao PIAO, Doctor of Engineering, Associate Professor, E-mail: psd@ybu.edu.cn

accepted 5 November 2015

Hydromechatronics Engineering

http://jdy.qks.cqut.edu.cn

E-mail: jdygcyw@126.com