Matlab与Excel联合求解堤防工程土料场规划的线性规划模型
刘 森,刘 琳
(1. 黑龙江省水利水电勘测设计研究院,哈尔滨150080;2. 山东省泗水县水利局,山东 泗水273200)
0 引 言
中国地域辽阔、河流众多。洪涝灾害自古以来不仅对人民生活的安全造成严重威胁,而且对于沿线农牧、渔业等生产造成危害,致使人民生命安全、财产得不到保障。人们对待洪涝灾害最有利的方法之一便是修建堤防工程。
堤防工程较枢纽、除险加固、灌区等工程最明显的特点便是沿线较长,工程呈线性分布。堤防工程的料场规划,尤其是沿线集中料场,一直是施工组织设计中的重点和难点。目前部分设计师对于堤防工程沿线集中料场的规划仍然是采用经验估算的方法。这种方法对于沿线较短的堤防或者料场单一的情况还能受用,但是对于沿线较长和料场较多的情况就大不一样。这不仅耗费大量时间、精力,而且对于计算的精度不能保证,对于投资控制不能给予更好的指导,造成资源的浪费和能源的消耗。目前解决堤防工程料场规划最有效的方法之一就是线性规划模型。
对于沿线较短和料场较少的情况,目前解法较多,比如单纯形法,Matlab 软件,Excel 自带的规划求解等。然而这些方法,对于沿线较长和料场较多的情况,由于决策变量较多(一般约有上百个),上述方法显然比较困难[1-2]。
文章讨论的主要问题就是针对沿线较长并且沿线集中料场较多的堤防的线性规划模型求解,即利用Matlab 自带的Excel-link 宏将数据输入至Matlab程序,然后利用Matlab 程序的linprog 函数来求解。本文所用的方法仍然适用于堤防工程沿线较短和料场较少情况。
1 线性规划模型简介
线性规划理论与方法目前已比较成熟,其一般形式为:
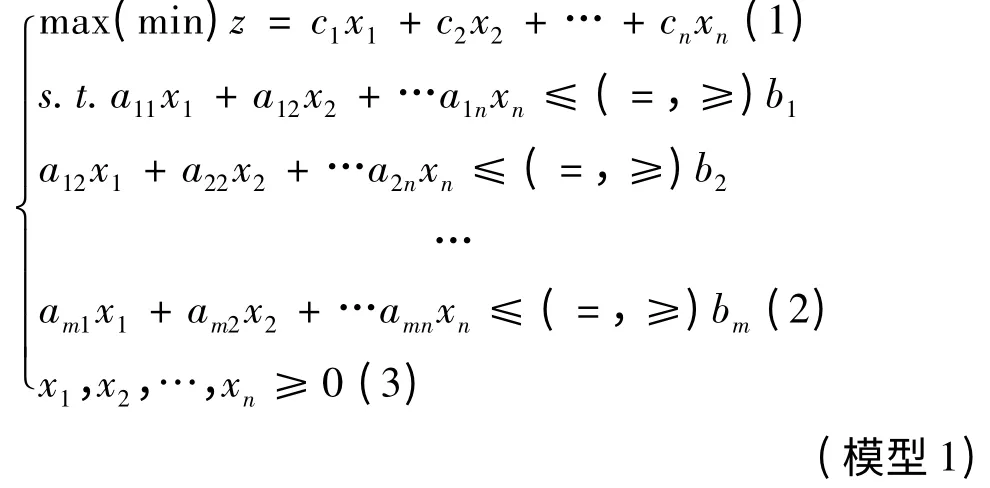
其中,式(1)为目标函数,有max 和min 两种形式;式(2)称为约束条件,它们表示问题受到各种约束,一般有三种形式:“≥”、“≤”(这两种约束又称不等式约束)或“等于”(又称等式约束);式(3)称为非负约束,很多情况下决策变量都蕴含了这个假设。
线性规划的模型还可以表示为下列矩阵形式:
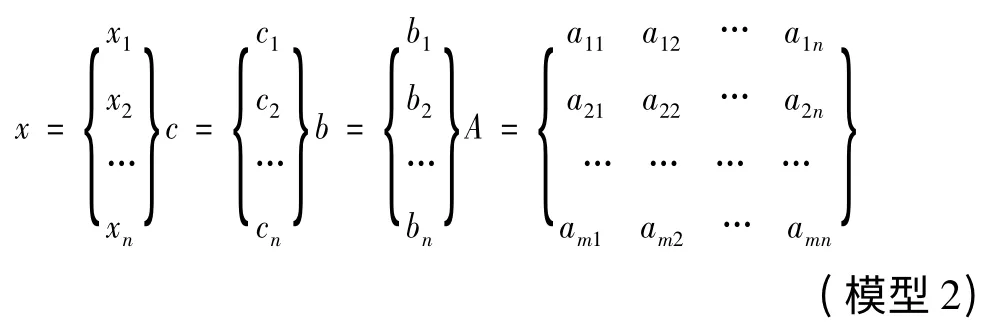
在上述模型中,x 为决策变量;c 为目标函数系数向量或价值系数向量或费用系数向量;b 为约束右端常数向量或简称右端项,也称资源常数向量;A 为约束系数矩阵或技术系数矩阵。
2 Mat lab 程序简介
Mat lab 是近来年得到快速发展的数学软件,它将高性能的数值计算和可视化集成在一起,并提供了大量的内置函数,被广泛的应用于科学计算、控制系统、信息处理等领域的分析、仿真和设计工作[3]。
文章所用到的函数为Mat lab 自带的linprog 函数,其数学模型为:

式中:f 为目标函数;A 为不等式约束的系数矩阵;b为不等数约束的右端项;Aeq 为等数约束的系数矩阵;beq 为等式约束的右端项;lb 为变量的下界;ub为变量的上界。
3 Excel-link 宏简介
Excel-link 宏是Matlab 软件提供的能与Excel互动操作的宏,它使得数据在Mat lab 和excel 之间随意交换,以及在Excel 下调用Mat lab 的函数[4]。
若Excel 程序未加载Excel-link 宏,可在Excel工具上→加载宏→浏览(Mat lab 的安装路径)→toolbox 文件夹→exlink 文件夹→excllink. xla 文件(打开),即可使用此宏。如图1 所示:
在Excel 工具条中出现startmatlab、putmatrix、getmatrix、evalstring,说明Excel-link 说明加载成功。
putmatrix:向Mat lab 中输入数据;getmatrix:从Mat lab 中获取数据。文章主要用到这两个命令。
4 应用实例
4.1 基本资料
黑龙江省某堤防填筑工程,沿线长110 km,堤防每5 km分一段,共22 段各段需土量见表1。沿线共有13个料场,编号为1 ~13,储量见表2。各个料场到各个堤防段的平均运距见表3。
4.2 数学建模
本项目决策变量较多为22 ×13 =284个,命名采用堤防段(行)与料场(列)编号进行。比如堤防编号01 与料场编号01,表示从料场01 向堤防01 的供料量,用x0101表示,依此类推,x0102表示从料场02号向堤防段01 号的供料量。
根据模型1,建立数学模型如下:
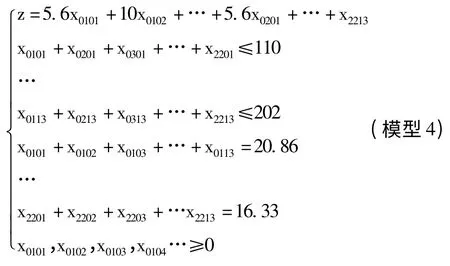
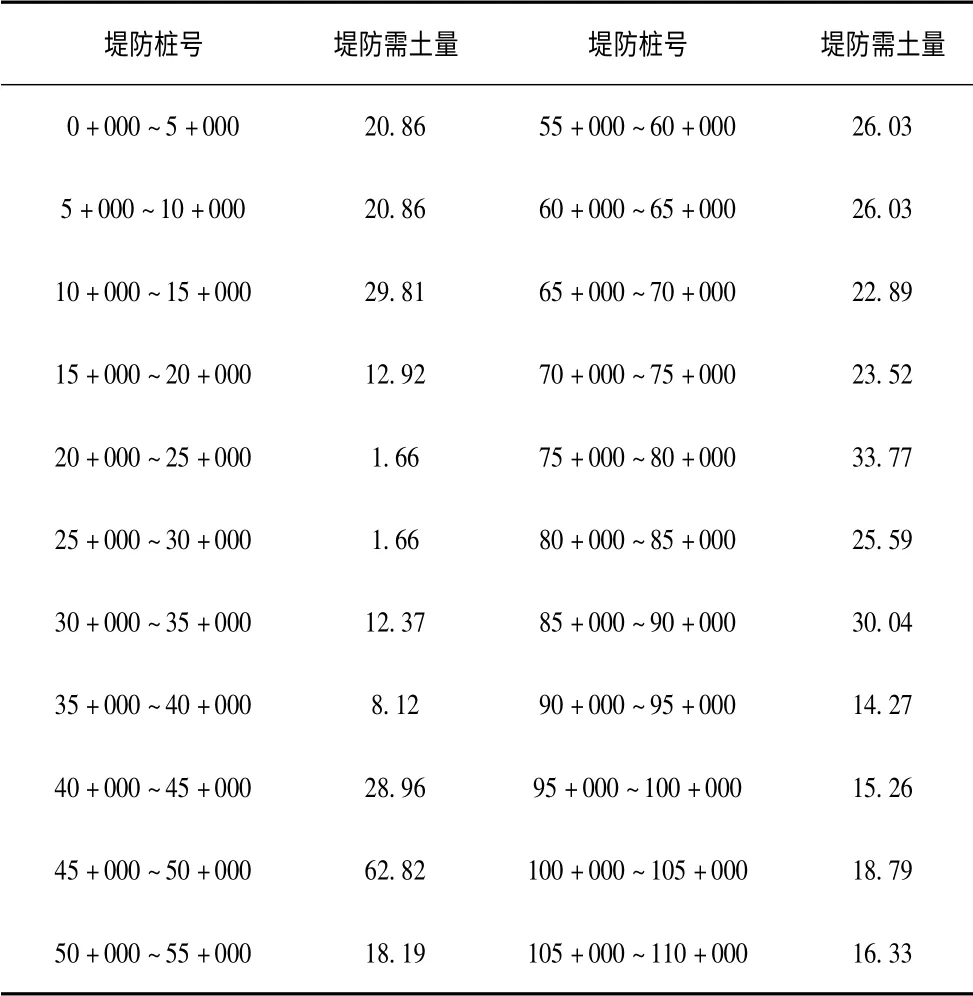
表1 堤防沿线分段需土量 万m3
为了方便Mat lab 计算,改用模型3 如下:

式中各含义与本文第三节“Matlab 程序简介”相同。
由于系数矩阵A 与Aeq 自变量个数较多为284个,而excel2003 版本以前,表格行数仅有256 行,因此数据在输入Mat lab 之前,需要将A 矩阵、Aeq 矩阵转置,等输入至Mat lab 之后再进行转置运算即可。A 矩阵与Aeq 矩阵变为:

4.3 利用excel 将数据输入Mat lab
首先选中要输入Mat lab 的数据源,如图2 所示。然后点击命令putmatrix,会弹出输入至Mat lab变量名称对话框,如图3 所示,可以键入任意名称,为了便于理解和下一步运算,建议输入A。接下来分别输入Aeq,f,b,beq,lb 至Mat lab。
图2 AT在excel 中的部分数据源
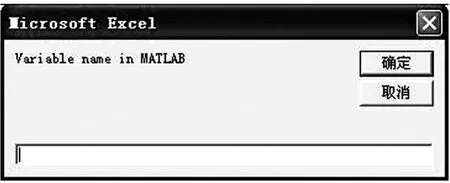
图3 数据输入Mat lab 数据的对话框
4.4 利用Mat lab 中linprog 函数计算线性规划
在Mat lab 命令窗口中键入[x,fval,exitflag,output,lambda]=linprog(f,A,b,Aeq,beq,lb,ub)

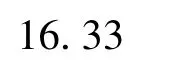
运算结果为:整理后数据见表4。
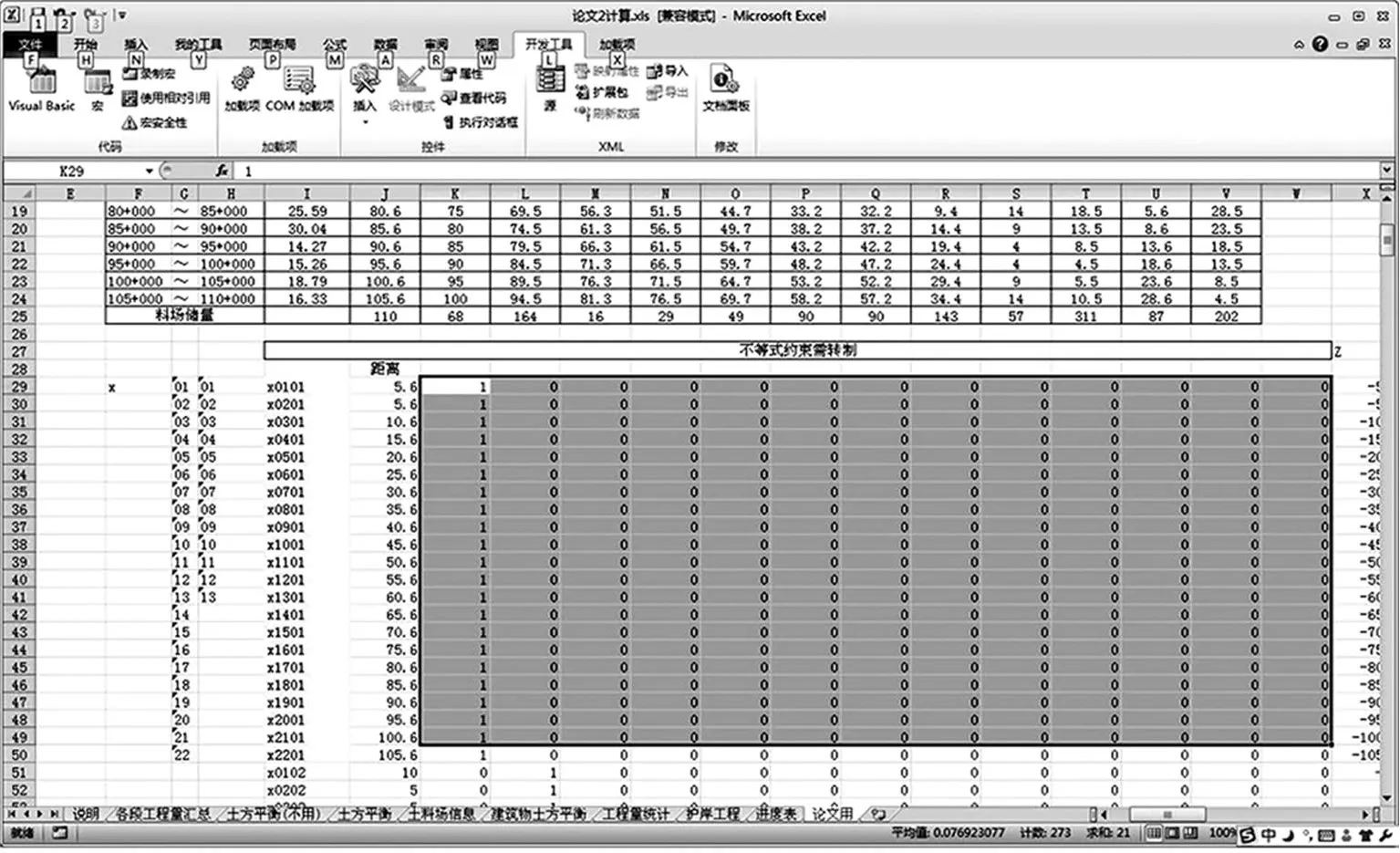
图1 加载宏示意图

表2 料场储量表 万m3
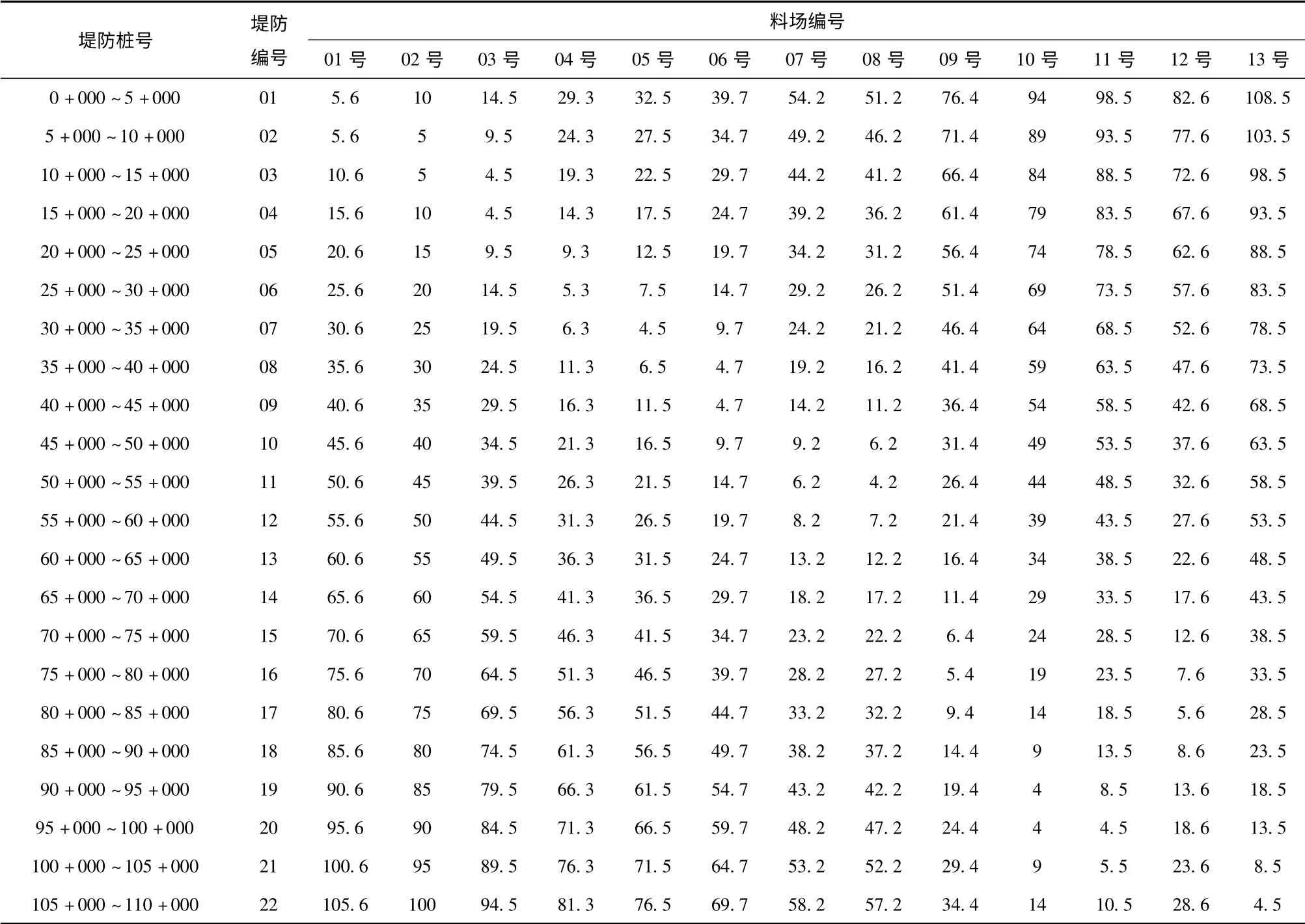
表3 各个料场至堤防段的平均运距 km
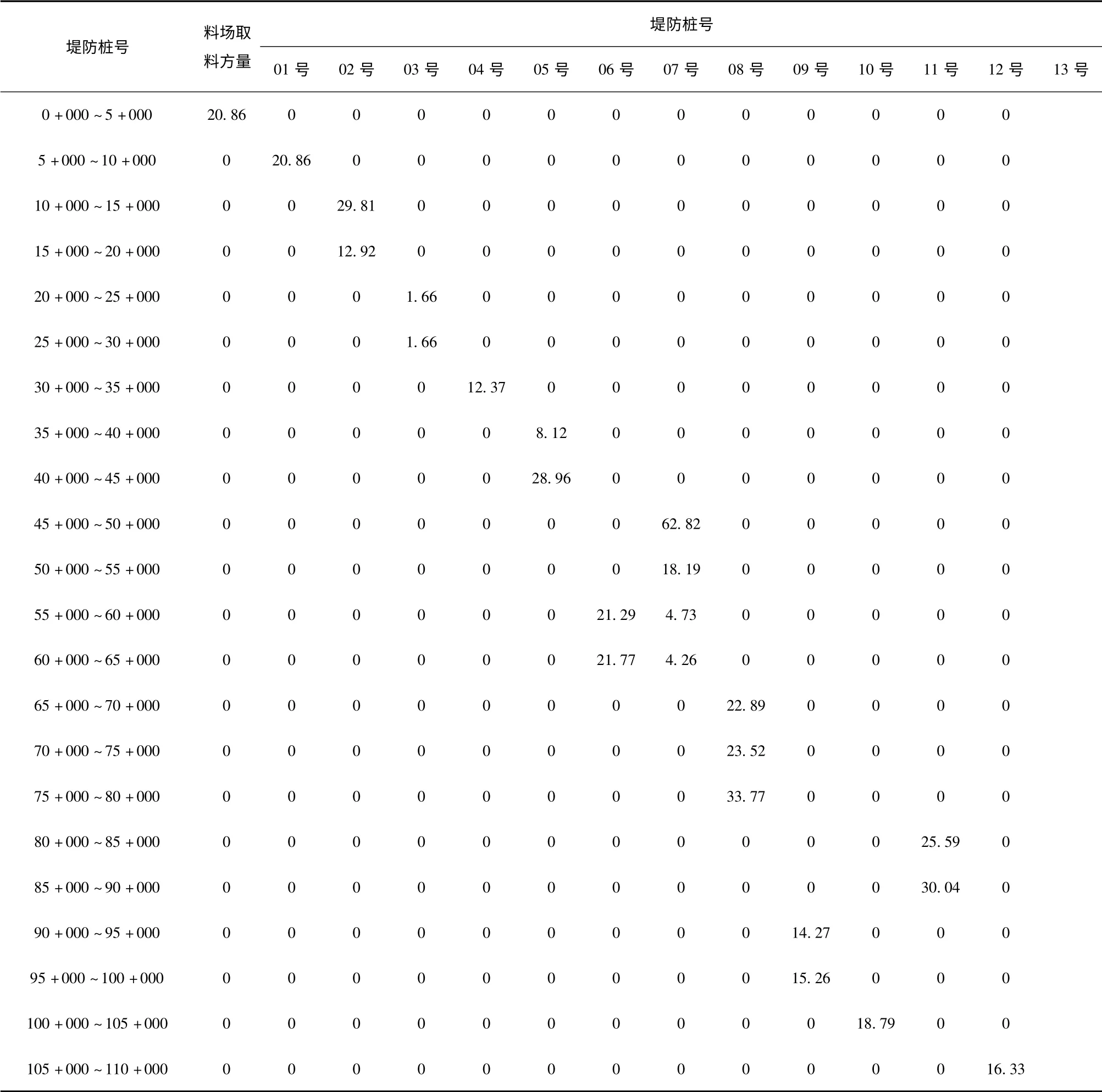
表4 运算结果整理数据列表 万m3
5 结 论
1)堤防工程沿线较长,线性规划模型能很好的解决多决策变量下的堤防工程料场规划问题,利用现代计算机运算速度快的特点,只要给Mat lab 给予准确的模型,就能很快的得出运算结果。
2)利用Mat lab 与Excel 联合求解多决策变量,看似步骤繁琐,但是利用Excel 强大的表格处理功能(本文没有介绍)能很快的将数据输入Excel 表格中,从而很容易将数据输入至Mat lab 程序中,思路清晰,便于理解,运算结果能较好的指导施工。
3)由表4 可以看出,运算结果一目了然,非常实用,对于更长堤防或者更多沿线料场的求解,效果更是明显。
[1]吴祈宗.运筹学与最优化方法[M]. 北京:机械工业出版社,2003:8.
[2]焦树锋. 线性规划的Excel 解法[J]. 滨州职业学院学报,2007(12):12 -16.
[3]王家文.Matlab7.0 编程基础[M]. 北京:机械工业出版社,2005:7.
[4]吴祈宗.运筹学与最优化MAT LAB 编程[M]. 北京:机械工业出版社,2003:8.

