翻边压电晶片激励Lamb波声场研究
许烨东 魏勤 智达
(江苏科技大学数理学院 镇江 212003)
翻边压电晶片激励Lamb波声场研究
许烨东魏勤†智达
(江苏科技大学数理学院镇江212003)
压电晶片广泛应用于超声波检测领域,是激励和接收超声波的最主要器件之一。本文用实验、有限元压电模拟和半解析数值模拟方法,研究翻边压电晶片在板中激励Lamb波声场。三种方法得到的Lamb波信号吻合性好,仅A0模式由于频散有少量差异。同时分析了翻边电极面积对声场分布以及声场能量的影响。翻边电极造成了Lamb波声场不对称,减少了声场的能量,同时降低了压电晶片的电容、机电耦合系数和品质因子等参数。
压电晶片,电极,Lamb波
1 引言
压电晶片是基于压电效应的声波驱动器与传感器,在传统的超声波检测领域有着广泛的应用。利用晶片厚度方向振动获得的超声波来检测材料和结构内部损伤,具有经济、实用、灵敏的特点。近年来,随着超声导波检测技术的兴起,用压电晶片激励和接收导波也获得了大量的应用[1]。国内外有许多学者将压电晶片作超声波传感器用于壳形构件的健康状态监测。V.Giurgiutiu的在结构健康监测中基于压电晶片的调谐Lamb波激励和检测一文中分析了压电晶片和板状材料界面剪应力分布,提出剪切滞后传递能量模型[2]。A.Raghavan等人回顾了导波检测技术,并重点讨论了在无损检测领域中使用压电晶片的导波检测技术[3]。在使用压电晶片的过程中,其电极的面积对压电晶片的整体性能有着重要影响,Miso结合理论和实验研究叉指电极尺寸和压电晶片的厚度对压电晶片能量转换的影响[4]。H.Huang等人的基于压电晶片驱动器产生位移场的Lamb波研究一文中,提出压电晶片力学模型,指出压电晶片的弯曲变形是产生Lamb波位移场的直接原因[5]。E.V.Glushkov等人研究压电晶片的选择性激励Lamb波模态的一文中,研究Lamb波模式选择性激励[6]。J.Moll等人通过实验研究激励信号的频率和步数对Lamb波影响,分析压电晶片的半径和厚度对Lamb波S0和A0模态能量的影响[7]。在此基础上,J.Moll进一步用钉扎力模型通过理论计算分析翻边压电晶片的电极角度、方位和焊点位置对激励Lamb波的声场分布的影响[8]。在压电晶片的应用过程中,采用翻边电极既可以方便电极的引出,焊接引线,又能在粘贴时使晶片更好地贴合结构表面,便于安装。
本文通过实验、有限元压电模型和半解析计算模型三个方法研究翻边压电晶片激励Lamb波,并用有限元压电模型分析翻边压电晶片电极面积对Lamb波声场分布的影响,并从时域和频域角度分析S0和A0模态信号,为压电晶片在超声导波检测应用提供参考。
2 理论基础
2.1压电效应
当压电材料承受一定机械应力时,其表面上会感应出电荷,材料将机械能转化为电能;另外压电材料加上电势后会使材料变形,统称为压电效应。该效应可用压电方程表示,即压电材料的本构方程,是反映压电晶体中力学参数(T,S)和电学参数(E,D)之间相互关系的方程组,分为四类,此处不赘述,公式(1)为其一的e方程
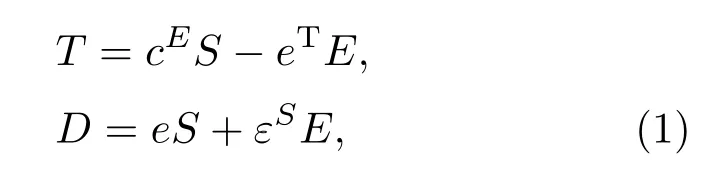
其中T为应力,D为电位移,S为应变,E为电场强度,c为弹性刚度常数,cE为场强恒定时的弹性刚度系数,e为压电应力系数,eT为e的转置,ε为介电常数,εS为应变恒定时的介电常数。
2.2板中Lamb波
导波是声波在介质中的不连续交界面间经多次往复反射,并产生复杂干涉和几何弥散效应而形成的一种弹性波。Lamb波是一种在激励声波波长与厚度为相同数量级的声波导中(如金属薄板)由纵波和横波合成的特殊形式的应力波。Lamb波是在薄板中传播的一种弹性波,根据质点位移分布的特点,自由板Lamb波传播的对称模态和反对称模态频散方程为
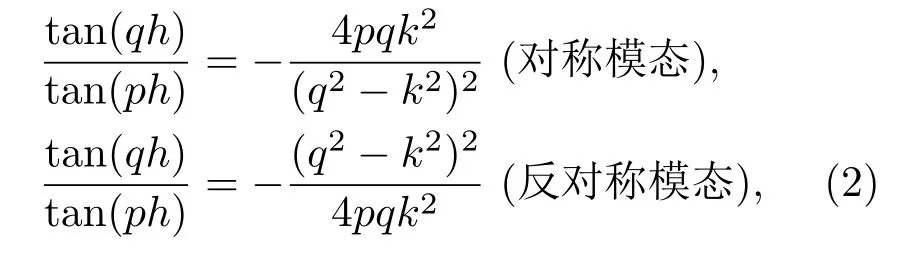
2.3结构模型和相关理论
Lamb波常用斜角探头、压电晶片以及叉指型表面波探头激励产生。斜角探头通过压电晶片厚度方向振动产生纵波斜入射到板内经波型转换产生纵波和横波,并由板上下表面多次反射产生Lamb波。压电晶片和叉指型表面波探头则通过板表面的剪应力产生的应力波在板内传播。V.Giurgiutiu的一文[2]提到压电晶片和板状材料之间通过界面的剪应力来激励Lamb波,即:τ(x,t)=τa(x)exp(iωt)。压电晶片和板材的模型如图1所示。
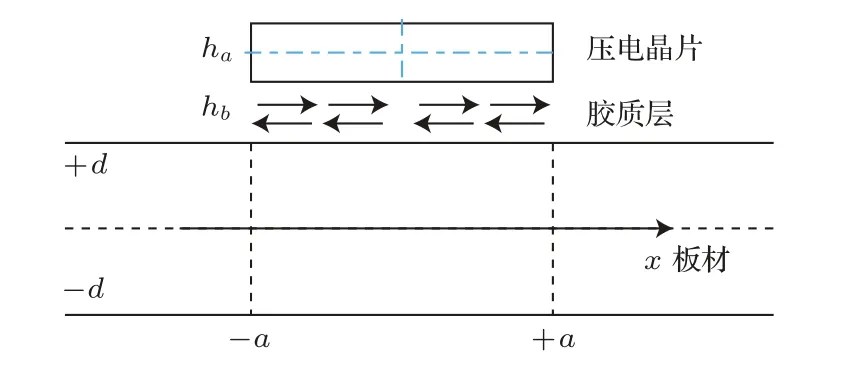
图1 压电片与板的相互作用模型Fig.1 Shear layer interaction between the PZT and the structure
剪应力的强度和分布依据于压电晶片和板材变形,当压电晶片和板状材料间存在胶质层时,其传递关系可以用双曲线函数表示,界面剪应力τ0(x)即:
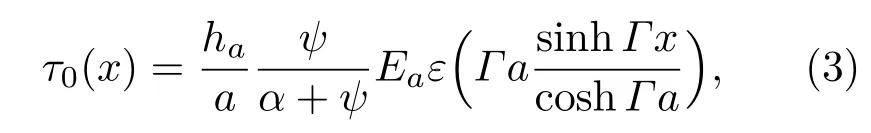
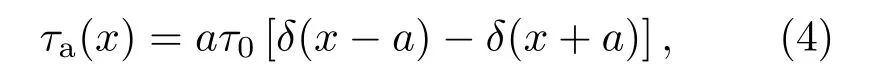
其中aτ0即为钉扎力,如图2所示。
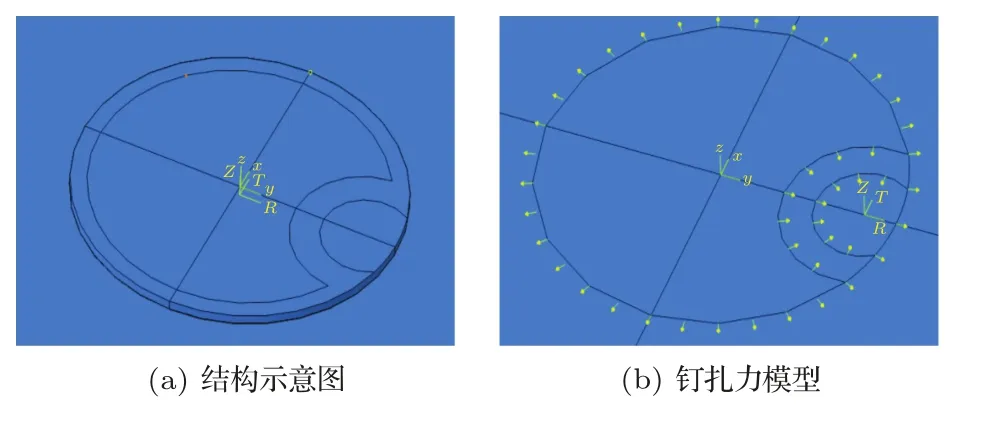
图2 数值计算模型Fig.2 Model for numerical calculation
E.V.Glushkov和J.Moll使用的钉扎力模型中压电晶片的非线性界面载荷可用矢量表示:
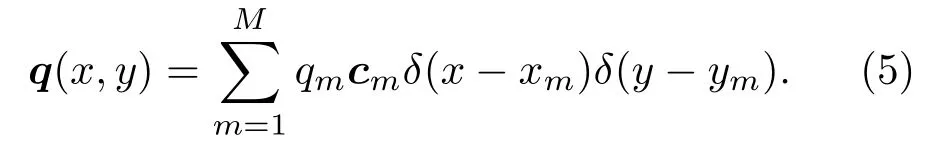
式(5)中(xm,ym)即为图2中的作用点,cm为单位矢量,且与xOy平面正交,qm为钉扎力大小。
3 压电晶片激励与接收Lamb波的实验及模拟
3.1实验
如图3所示,实验选用尺寸大小为600 mm× 600 mm×1.5 mm的铝板,铝板中部表面位置粘贴直径10 mm、厚度0.25 mm的压电晶片PZT1和PZT2(间隔200 mm),压电晶片型号为PZT-5H。压电晶片的电极是翻边的,胶质层为环氧树脂和聚酰胺树脂一比一混合。压电晶片PZT1用幅值为50 V的Hanning窗五步波信号激励(中心频率为200 kHz),窗函数为公式(6),压电晶片PZT2用于接收导波信号,并用示波器采集波形。

图3 实验图Fig.3 Experimental photo
Hanning窗函数:
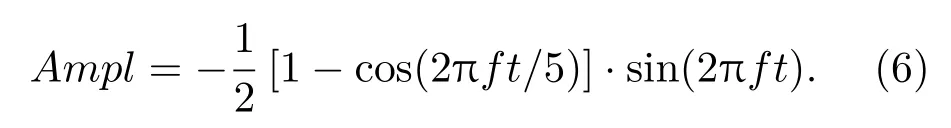
其中,Ampl为幅值,f为中心频率,t为时间。
3.2有限元压电模型
Abaqus有限元模拟压电晶片激励模型如图4所示。在图4(a)600 mm×600 mm×1.5 mm的铝板上粘贴间隔200 mm的两压电晶片,其形状的规格如图4(b)所示,晶片的电极是翻边的。晶片与铝板之间有直径10 mm,厚度0.01 mm胶质层,相互约束为TIE。PZT1作激励驱动器,并在PZT2处接收信号。有限元模拟所施加电势同实验信号。晶片网格划分的单元类型为Piezoelectric(C3D8E),铝板和胶质层单元类型为3D Stress(C3D8R),单元长度均选择1 mm,计算时间步长为0.1µs。
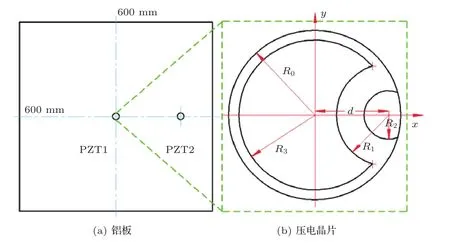
图4 有限元模拟的平面图(R0=5 mm,R1=2.3 mm,R2=1.4 mm,R3=4.5 mm,d=4.1 mm,h=0.25 mm)Fig.4 Planar graph of the simulation(R0=5 mm,R1=2.3 mm,R2=1.4 mm,R3=4.5 mm,d=4.1 mm,h=0.25 mm)
Abaqus有限元中所需的压电晶片、胶质层和铝板的材料参数见表1和表2.
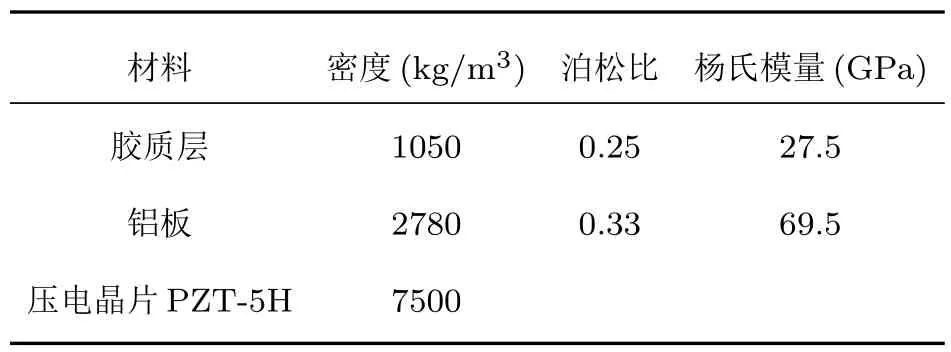
表1 材料参数Table 1 Material properties

表2 压电晶片参数Table 2 Properties of PZT-5H
3.3半解析模型
建立同图4(a)的铝板模型,其材料参数如表1所示。在铝板中心区域设置压电晶片形状的激励区域,并在其边缘按要求设置钉扎力,其幅值用Hanning窗函数调制。如图2所示,在电极大圆上施加的钉扎力是小半圆上的四倍。计算时间步长与有限元压电模型一致。
3.4实验与模拟结果
采集实验中PZT2晶片的电信号,有限元压电模型中PZT2的电势,以及半解析模型PZT2晶片中心处单元节点的位移信号,并分别按各自信号最大值进行归一化,结果如图5所示。
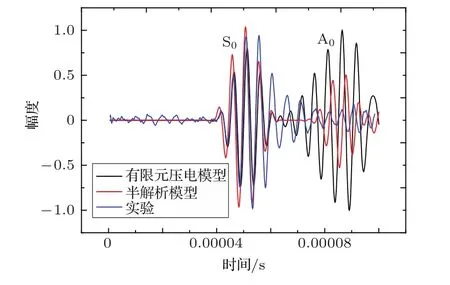
图5 有限元压电模型、半解析模型和实验信号对比图Fig.5 Comparison of finite element model,semianalytic model and experiment
由图5可知实验、半解析模型和有限元压电模型的结果还是比较接近的,尤其S0信号非常吻合。三种方法得到的S0模式和A0模式最大幅值比分别为:5.45,2.06,0.81。究其原因主要是实验信号中以离面位移为主导的A0模态能量会向空气中泄漏,加上频散,因此A0模态波包幅度小;半解析模型的激励源是沿径向的钉扎力,其对S0模态的贡献大,钉扎力产生的力矩激励A0模态;有限元压电模型中晶片边缘的剪应力可以等效为钉扎力,晶片厚度方向上的变形也有助于激励A0模态,导致该模型A0模态波包幅度最大。综上结果,可以看出用有限元压电模型方法模拟翻边压电晶片激励Lamb波结果与实验、理论接近,具有较高的可靠性。下面则用该模型研究晶片电极变化时的Lamb波声场。
4 电极面积对压电晶片声场影响
4.1仿真模型
为了研究电极面积对压电晶片声场的影响,建立不同电极的有限元压电模型,如图6所示,研究的变量为压电晶片电极面积,其中#1压电晶片电极完全对称,上下表面是两块完整的圆形电极,其他三个模型#2、#3、#4电极是翻边的。四个压电晶片模型表面小电极和大电极的面积比分别约为0.00、0.03、0.10和0.60。在翻边压电晶片的实际使用过程中,为了确保晶片足够多的区域产生压电效应,小电极面积不宜大,方便焊接即可。
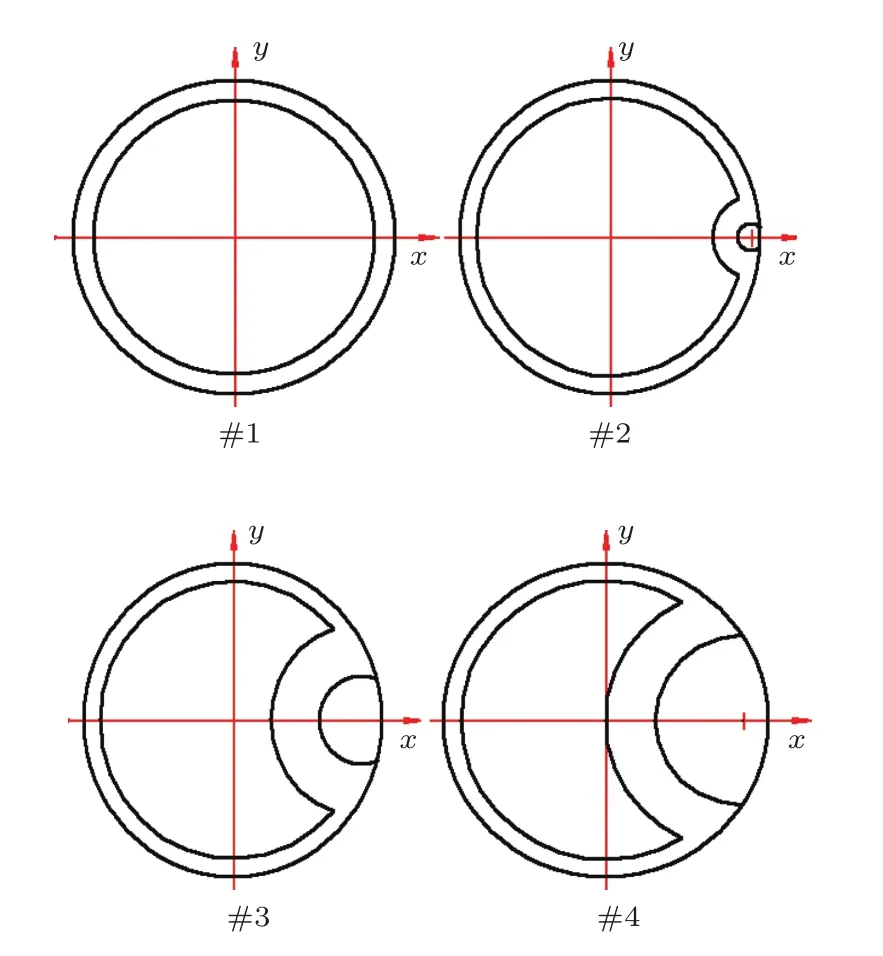
图6 不同的压电晶片模型Fig.6 Piezoelectric wafer models
4.2模拟结果
4.2.1压电晶片电极面积对时域波形的影响
(1)激励的模态分析
图7(a)为模型#1铝板中Lamb波产生的径向位移U1信号到达距离正中心100 mm处的云图,图7(b)为100 mm处的时域图。
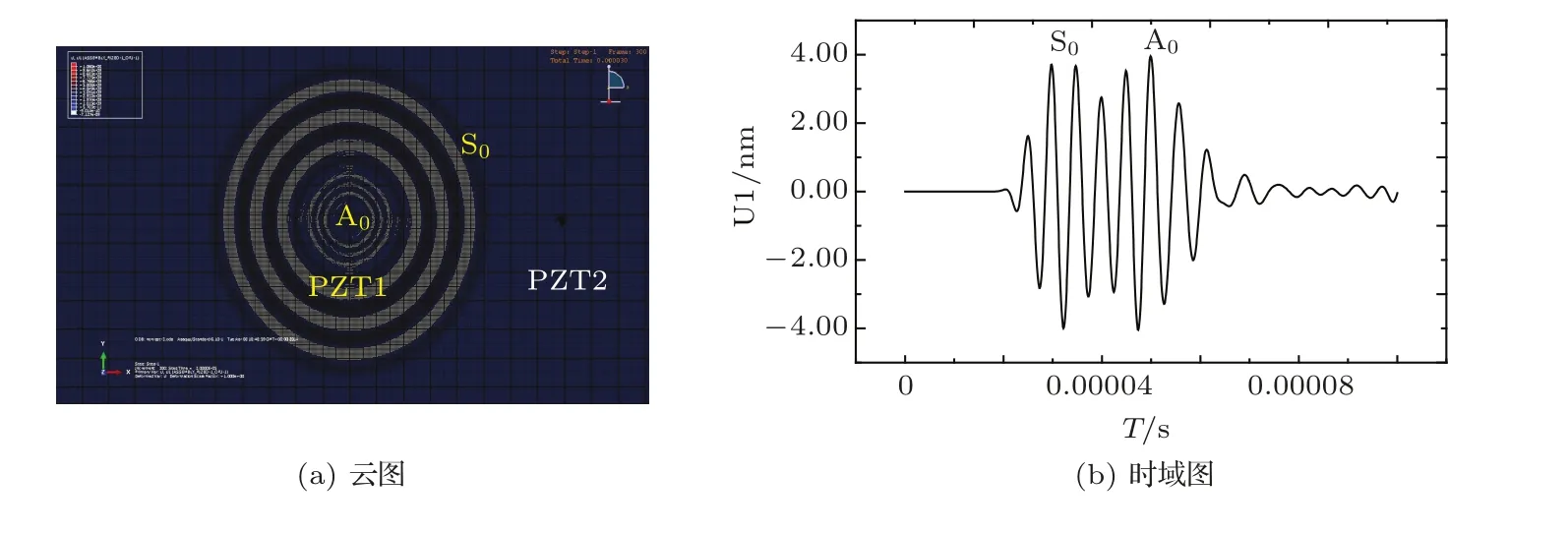
图7 模型#1的声场Fig.7 Sound field of model#1
由图7数据可以计算出第一个波包(S0)信号到达100 mm处的传播速度,约为5000 m/s(与S0的理论值5300 m/s接近);第二个波包(A0)信号到达100 mm处的传播速度,约为2500 m/s(与A0的理论值2600 m/s接近)。
(2)电极对时域波形的影响
为了比较Lamb波幅度的变化,采集四个模型传播方向距离200 mm处表面的径向位移U1数据,如图8所示。
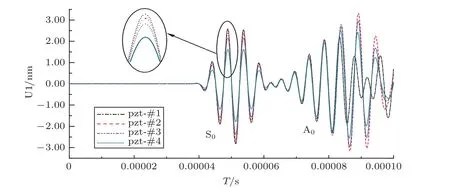
图8 四个模型的U1信号(200 mm)Fig.8 Signals of four models(200 mm)
观察第一个波包(S0),可以发现,从模型#1到模型#4,信号整体幅值逐渐减小,即当压电晶片上表面小电极面积越来越大时,压电晶片中产生压电效应所需电场的区域越来越小,信号幅度也越来越小。由图8可知第二波包A0模式在此频率处频散严重,波包变形失真,波包幅值无明显规律。
4.2.2电极面积对Lamb声场的影响
采集模型#1和#3中当波传播至距板中心100 mm圆周上时各点的径向位移U1信号幅值,并作图,如图9所示。
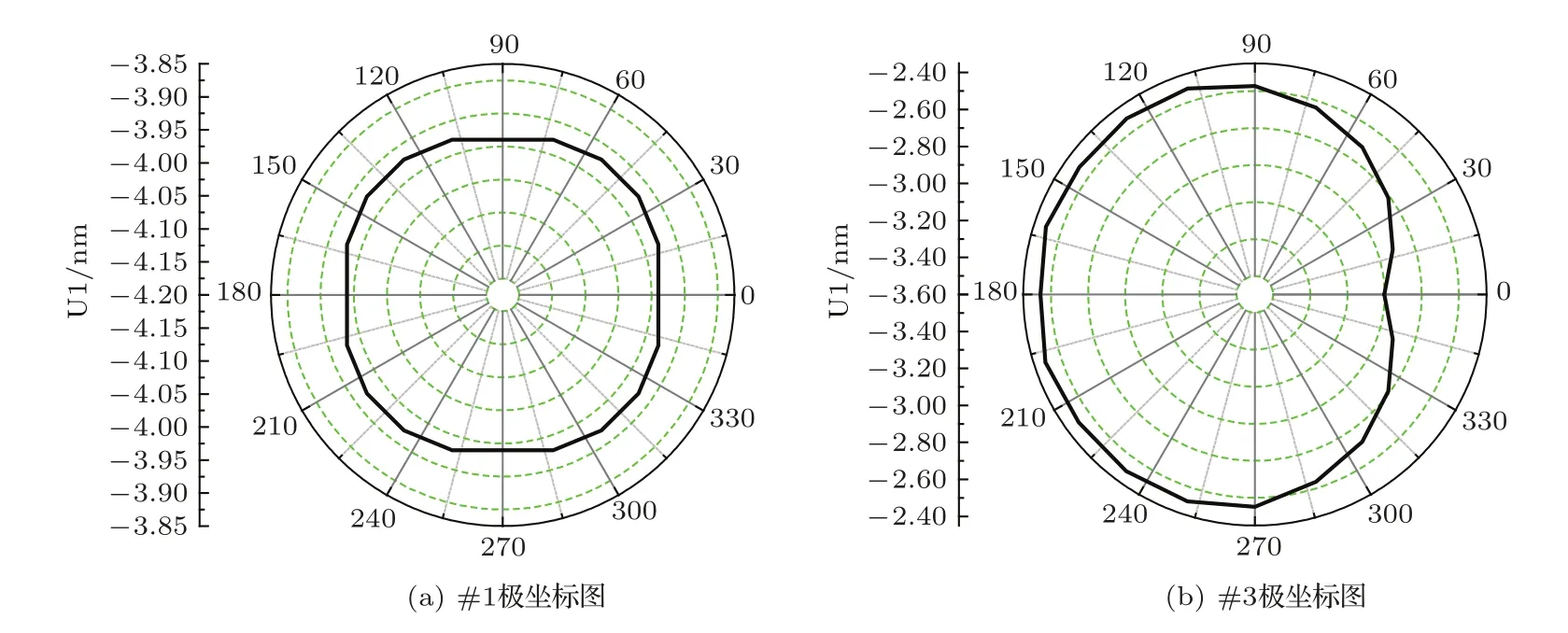
图9 #1极坐标图和#3极坐标图Fig.9#1 polar plot and#3 polar plot
对比压电晶片#1、#3模型图和图9的极坐标图,不难发现,模型#1的极坐标图非常对称,近似圆,而模型#3的极坐标图则因有了翻边电极的存在而不完全对称,且在翻边电极一端方向(0°)上U1幅值明显比其他方向小(0°方向上最小,180°方向上最大)。其原因是晶片翻边电极改变该处施加在晶片上的电势场,进而影响了压电效应产生的应力场。
4.2.3电极面积对频域波形的影响
取图8中第一个波包(S0),做快速傅里叶变换,得到其频谱,如图10所示。
由图10可以发现,4个曲线的中心频率都是约为200 kHz,而且也能得到类似的结论:当压电晶片翻边电极面积越来越大时,S0信号中心频率处的幅值越小,即当翻边电极晶片的面积比增大时,所激励的Lamb波声场能量减小,导致激励时压电晶片储存电能的能力减小,即电容减小,并进一步影响有效转化为机械能的大小,使得压电晶片的机电耦合系数和品质因子都减小。因此,采用翻边电极虽然方便电板的引出,粘贴时能更好地贴合铝板,但这是以牺牲压电晶片能量转化效率为代价的。
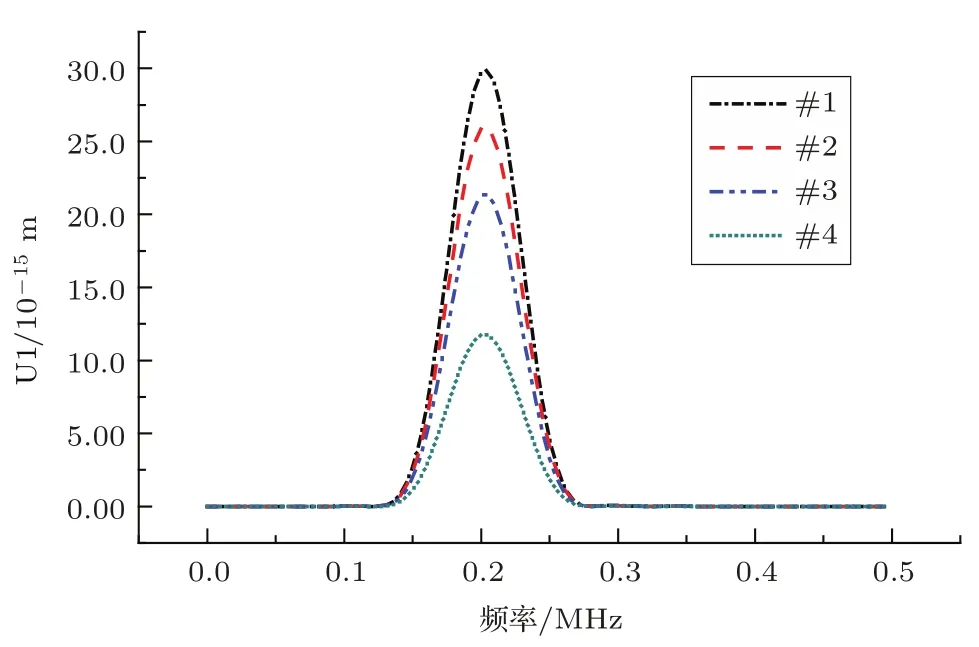
图10 4个模型的U1信号(S0)频谱(200 mm处表面)Fig.10 Frequency spectrum of U1 signals(S0)(200 mm at the surface)
5 结论
本论文结合实验和半解析模拟,通过有限元压电模拟方法,研究翻边电极对压电晶片声场影响,得到以下结论:
(1)实验、有限元压电模拟和半解析模拟得到的S0模式信号吻合较好,但A0模式因频散等原因有差异。
(2)声场分布因压电晶片有翻边电极的存在而不完全对称,且在翻边电极一端方向(0°)上幅值明显比其他方向小(0°方向上最小,180°方向上最大)。
(3)当压电晶片翻边电极面积比越大时,电容、机电耦合系数、品质因子、能量转换效率、S0时域和频域信号幅值越小。
在设计压电晶片的过程中,满足使用的条件同时,应尽可能减小翻边电极的面积,而且使用时要注意晶片的固定方向。本论文的研究存在很多局限性,关于电极对压电晶片的声场的研究还有很多方面可以探索,例如可以深入研究电极厚度对压电晶片Lamb声场的影响。
[1]GIURGIUTIU V.Structural health monitoring with piezoelectric wafer active sensors[M].London:Elsevier,2008.
[2]GIURGIUTIU V.Tuned Lamb wave excitation and detection with piezoelectric wafer active sensors for structural health monitoring[J].Journal of Intelligent Material Systems and Structures,2005,16(4):291-305.
[3]RAGHAVAN A,CESNIK C E S.Review of guided wave structural health monitoring[J].The Shock and Vibration Digest,2007,39(2):91-114.
[4]HUANG H,PAMPHILE T,DERRISO M.The effect of actuator bending on Lamb wave displacement fields generated by a piezoelectric patch[J].Smart Materials and Structures,2008,17(5):1-13.
[5]GLUSHKOV E V,GLUSHKOVA N V,KVASHA O V,et al.Selective Lamb mode excitation by piezoelectric coaxial ring actuators[J].Smart Materials and Structures,2010,19(3):035018.
[6]KIM M.Effect of electrode configurations on piezoelectric vibration energy harvesting performance[J].2015,24(4):045026.
[7]MOLL J,FRITZEN C P.Advanced aspects of modeselective excitation of ultrasonic guided waves[C].24th conference on noise and vibration engineering,Leuven,Belgium,2010.
[8]MOLLA J.Non-axisymmetric Lamb wave excitation by piezoelectric wafer active sensors[J].Sensors and Actuators A,2012,174:173-180.
Research on Lamb wave excited by flanging piezoelectric wafer
XU YedongWEI QinZHI Da
(Department of Physics,Jiangsu University of Science and Technology,Zhenjiang 212003,China)
The piezoelectric wafer is being more and more widely used in the ultrasonic detecting technology. It's one of the most significant devices to generate and receive guided waves.In this paper,the Lamb wave is excited and received in plate by using flanging piezoelectric wafer.The principle is studied in detail via experiment,finite element simulation and semi-analytic solution.The three solutions match perfectly in the Lamb wave signal but have some differences in A0mode because of dispersion,et al.The effects on wave field distribution and energy by wafer's electrodes are also analyzed.The wave field changes with the area ratios of electrodes.Due to the flanging electrode,the acoustic field distribution is incompletely symmetrical.The energy of the wave field and the piezoelectric wafer's capacitance,electromechanical coupling factor,quality factor,and the others change with the electrode area ratios.
Piezoelectric wafer,Electrode,Lamb wave
TG115.28
A
1000-310X(2015)06-0547-07
10.11684/j.issn.1000-310X.2015.06.011
2015-04-13收稿;2015-07-04定稿
许烨东(1990-),男,江苏江阴人,硕士研究生,研究方向:物理电子学。
E-mail:future_good@163.com

