二维蜂窝结构声子晶体的负折射成像研究∗
林 建 吴福根 姚源卫 张 欣
(1广东工业大学实验教学部 广州 510006)
(2广东工业大学物理与光电工程学院 广州 510006)
二维蜂窝结构声子晶体的负折射成像研究∗
林 建1,2吴福根1†姚源卫2张 欣2
(1广东工业大学实验教学部广州510006)
(2广东工业大学物理与光电工程学院广州510006)
为了得到分辨率更好的平板透镜,利用有限元的方法研究了由水/水银材料组合的二维蜂窝结构声子晶体平板透镜的负折射成像特性,通过数值仿真计算了声子晶体的能带结构、等频色散曲线,模拟了点源成像,并且利用高斯波束验证了声子晶体平板透镜的负折射现象,得到了有效折射率neff=-1的成像。对比相同材料的正方晶格和三角晶格而言,该模型的成像效果更佳。为了改善成像分辨率,还在原来的模型上进行了改进,得到了分辨率约为0.37λ的亚波长像。
声子晶体,负折射,蜂窝结构,成像
1 引言
声子晶体是一种新型人工功能材料,早期研究主要基于它的声子禁带,在禁带范围内的弹性波将被禁止传播,由于这一特殊性质,可利用它来制作隔音材料、声波导等[1-5]。近年来,人们开始把研究转向声子晶体的通带,因为通带也有很多有用的性质,如负折射、自准直[6]等。关于负折射的研究起源于左手材料的兴起,在1968年,前苏联物理学家Veselago首次提出左手材料的概念[7],并分析了它所具有的一些特殊性质,如反斯涅尔定律、逆多普勒效应、反切伦科夫效应等。但是由于在自然界中未能找到这样的物质,所以并没有被人们重视,直到Pendry提出可利用金属线阵列和开口环共振器阵列组合实现介电常数和磁导率同时为负值[8-9],负折射率材料的研究才被人们重视,并取得了丰硕的成果[10-13]。后来人们又在光子晶体中发现了负折射现象,同样在理论上和实验上也取得了重大进展[14-20]。
在声子晶体方面,近十年来,负折射的研究得到飞速发展[21-25]。张向东等人利用刚/空气和水/水银首次在二维正方晶格声子晶体中实现了第一能带的负折射成像并在水/水银体系中找到了全角负折射区域[26]。邱春印等人在固液二维三角晶格声子晶体中得到了第二能带的负折射成像,并通过改变填充率的方法使得有效折射率为-1,实现远场成像[27]。荔静等人首次使用二维三组元的模型得到低频带的负折射现象[28]。何兆剑等人引入表面调节突破衍射极限,实现亚波长成像[29]。然而,在声子晶体中关于六角蜂窝结构的负折射研究尚未见报道,本文通过有限元的方法计算了六角蜂窝结构能带结构及等频色散曲线,并利用点源及高斯波束进行了模拟仿真,结果表明利用六角蜂窝结构可以实现neff=-1的负折射成像:并且发现在这结构中可实现理想成像[27],而利用相同材料在正方晶格和三角晶格中的成像效果较差,未能实现理想成像,并且利用三角晶格及正方晶格所得到的平板透镜分辨率不高。所以本结构值得进行研究,同时,研究还发现对原来的蜂窝结构进行改善,能进一步提高成像分辨率。
2 模型及模拟仿真
2.1模型
图1给出了水/水银的声子晶体模型,其中蓝色部分为水,灰色部分为水银。该模型由水圆柱散射体以六角蜂窝晶格排列在水银基体中形成,其中最近邻的圆柱之间距离为a,圆柱半径为0.35a,填充率为0.296。材料参数如下:水密度ρ=1.0×103kg/m3,声速c=1.49 km/s;水银密度ρ=13.5×103kg/m3,声速c=1.45 km/s。为了实际可行,在水圆柱外层加上很薄的橡皮包层,其材料参数与水相仿,所以可忽略其影响。

图1 六角蜂窝结构声子晶体模型Fig.1 Configuration of phononic crystal with honeycomb-lattice
2.2能带结构
如图2所示,计算了单胞的色散关系,纵轴为归一化频率,横轴为波矢,从Γ点出发的直线为水银的色散线,与第二能带相交于频率为0.2427(2πc/a)处。从能带结构上看,第二能带的带顶较平,频率较低,并且关于Γ点附近对称性较好,所以在此频率附近将出现负折射现象[14,28]。

图2 水/水银蜂窝晶格的能带结构图Fig.2 Band structure for the designed phononic crystal consisting of water cylinders in mercury background arranged in honeycomb-lattice
2.3等频色散曲线
图3描绘了第二能带以Γ点为圆心的等频色散曲线,因为等频色散曲线表征了声波在声子晶体中的传播特性,其法线方向就是能量传播的方向,也就是群速度的方向,而相速度的方向则沿波矢方向,当两者方向相反时,将出现负折射现象。由图3可见在频率范围0.2158~0.2455(2πc/a)内的等频线非常接近为圆,这表明了在这频率范围内,声子晶体可视为各向同性介质,从而可以定义有效折射率[28]neff=-|k|c/ω。由于Γ点为高频率点,群速度方向沿法向向内,而相速度则沿波矢方向从Γ点沿法向向外,所以群速度与相速度反向,在此频率范围附近将会出现负折射现象。另外给出了该频率的水银的等频圆(黄色),发现其大小与声子晶体的几乎一样。这表明了在0.2255(2πc/a)频率处得到了有效折射率neff=-1的情况。

图3 声子晶体第二能带的等频色散曲线图Fig.3 EFCs of the designed phononic crystal for some frequencies at the second band
2.4高斯波束仿真
为了直观看到负折射现象,高斯波束被用来进行了仿真模拟,结果如图4所示,所使用的声子晶体平板大小为92(行)×12(层),其表面法向为ΓM方向(接下来的模拟仿真都取此方向,不再赘述),利用有限元的方法进行仿真,高斯波束从左下方入射,入射角为α=30°,频率为0.2255(2πc/a)。用带箭头的黑线描绘了高斯波束的传播路径,高斯波束在平板两界面都发生了负折射,最后从平板右边出射,出射角为β=30°,方向与入射方向保持一致。图中虚线为法线,可见入射波和折射波居于法线同侧,由此可证明所研究的模型确实存在负折射现象。但是仿真结果也显示透射波束较弱,绝大部分能量被反射掉了。

图4 高斯波束仿真图Fig.4 Simulation by Gaussian beam
2.5点源模拟
在声子晶体平板左端放置一个点源,频率为0.2255(2πc/a),使用了12层的平板,板厚为8.7a。物距设置为1.05a,如图5(a)所示,结果显示在板右端成像,测得像距为7.15a,物距与像距的和为8.2a,与板的厚度近似。再改变点源位置,使物距分别为4.15a和6.15a,得到的结果显示,像距分别为4.35a和2.25a,物距与像距之和与板的厚度接近,表明设计的声子晶体平板的有效折射率近似为-1。此外,保持物距为6.15a,使板的厚度分别为12层,16层和20层,得到的结果如下:16层板厚为11.7a,所得像距为5.2a;20层板厚为14.7a,像距为8.35a。可见点源位置以及板的厚度对折射率并无影响。

图5 点源仿真图Fig.5 Simulation with a point source
图5(b)、5(c)分别给出了用同样材料在正方晶格和三角晶格中的成像仿真,与蜂窝晶格相比,其成像效果较差,且未能实现理想成像。导致这种差别的主要原因是晶格结构的差异使得能带结构和等频色散曲线不同,在三角晶格和正方晶格中并没有得到满足条件的等频圆,所以无法得到理想成像。
为了研究模型的成像分辨率,进一步描绘了图5(a)中像点位置沿y方向上的声场分布强度图。如图6所示,圆柱半径为0.35a,点源距离平板为1.05a,结果显示像点处强度比较低,约为0.06 W/m2,半高全宽[30](Full widths at half maximum,FWHM)为3.93a,分辨率为0.88λ。

图6 像点处y方向的强度分布图Fig.6 Intensity distribution along y-direction at the image
3 改进模型及结果分析
为了提高成像分辨率,在原模型两边都加上一排水柱子,如图7所示。所用材料及参数不变,蓝色环形为水,灰色部分为水银。大圆柱半径R为0.35a,小圆柱半径r取值为0.01a~0.2a,小圆柱距离大圆柱d为1a。通过点源的模拟仿真,发现其成像强度在一定范围内随r的增大而增强(如图8所示)。

图7 改进模型结构图Fig.7 Configuration of improved phononic crystal with honeycomb-lattice
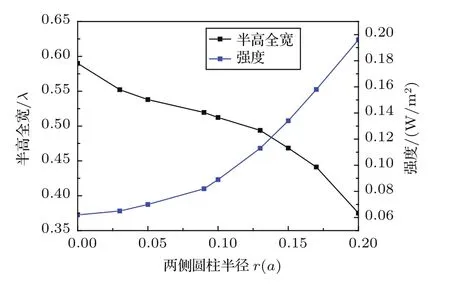
图8 半高全宽及强度随两侧圆柱半径变化图Fig.8 Variation of FWHM and intensity by changing the value of bilateral radius
进一步研究其分辨率的变化,图8还给出了像点的FWHM随r的变化,FWHM的大小表征了成像分辨率的情况,它的值越小,表明分辨率越高。保持R=0.35a不变,得到的结果表明在一定范围内,FWHM随着r增大而减小,在r=0.2a时取得最好的分辨率,约为0.37λ。
这种改进模型能改善成像分辨率的原因是它在小圆柱和大圆柱之间产生了声表面波,由于声表面波在一定程度上可以恢复点源的衰逝模式,所以成像质量就可以得到改善了。为了证明此观点,图9描绘了超元胞的能带结构(超元胞的结构如图7红框所示),蓝色实线为基体水银的色散线,红色虚线为由于增加了两排小圆柱而产生的声表面波模,它位于工作频率0.2255(2πc/a)附近,因此对成像质量的改善起关键作用。

图9 超元胞能带结构图Fig.9 Band structure for the chosen supercell
4 结论
本文利用水/水银的材料组合设计了蜂窝结构的声子晶体平板,并通过有限元的方法计算了能带结构和等频色散曲线,及高斯波束的负折射和点源成像的仿真模拟。结果表明利用六角蜂窝结构可以实现neff=-1的负折射成像:并且发现在这结构中可实现完美成像,而利用相同材料在正方晶格和三角晶格中的成像效果较差,未能实现完美成像,并且利用三角晶格及正方晶格所得到的平板透镜分辨率不高。通过在两边加柱子对模型进行改进,发现在相同条件下,改进模型可改善成像的分辨率。最后,本文所做的工作有望为以后实现声子晶体平板透镜的设计应用提供一定理论指导。
[1]WU F G,LIU Z Y,LIU Y Y.Splitting and tuning characteristics of the point defect modes in two-dimensional phononic crystals[J].Phys.Rev.E.,2004,69(6):066609.
[2]LIU Z Y,ZHANG X X,MAO Y W,et al.Locally resonant sonic materials[J].Science,2000,289(5485):1734-1736.
[3]ZHONG L H,WU F G,LI X L,et al.Effect of symmetry on sonic band-gap in two-dimensional phononic crystals[J].Journal of Inorganic Materials,2006,21(1):29-34.
[4]HUANG P P,YAO Y W,WU F G,et al.Numerical study of Lamb waves band structure in one-dimensional phononic crystal slabs with the anti-symmetric boundary structure[J].J.Appl.Phys,2014,115(6):063510.
[5]CHENG C,WU F G,ZHANG X,et al.Phononic crystal multi-channel low-frequency filter based on locally resonant unit[J].Acta Phys.Sin.,2014,63(2):024301.
[6]KOSAKA H,KAWASHIMA T,TOMITA A,et al.Selfcollimating phenomena in photonic crystals[J].Appl. Phys.Lett.,1999,74(9):1212-1214.
[7]VESELAGO V G.The electrodynamics of substrances with simultaneoursly negative values of ε andµ[J].Sov. Phys.Usp.,1968,10(4):509-514.
[8]PENDRY J B,HOLDEN A J,ROBBINS D J,et al. Magnetism from conductors and enhanced nonlinear phenomena[J].IEEE Trans.Microwave Theory Tech.,1999,47(11):2075-2084.
[9]PENDRY J B.Negative refraction makes a perfect lens[J]. Phys.Rev.Lett.,2000,85(18):3966-3969.
[10]SMITH D R,PADILLA W J,VIER D C,et al.Composite medium with simultaneously negative permeability and permittivity[J].Phys.Rev.Lett.,2000,84(18):4184-4187.
[11]SHELBY R A,SMITH D R,SCHULTZ S.Experimental verification of a negative index of refraction[J].Science,2001,292(5514):77-79.
[12]FOTEINOPOULOU S,ECONOMOU E N,SOUKOULIS C M.Refraction in media with a negative refractive index[J].Phys.Rev.Lett.,2003,90(10):107402.
[13]HOUCK A A,BROCK J B,CHUANG I L.Experimental observations of a left-handed material that obeys snell's law[J].Phys.Rev.Lett.,2003,90(13):137401-1-137401-4.
[14]LUO C Y,JOHNSON S G,JOANNOPOULOS J D,et al. All-angle negative refraction without negative effective index[J].Phys.Rev.B,2002,65(20):201104-1-201104-1-4.
[15]LUO C Y,JOHNSON S G,JOANNOPOULOS J D,et al.Subwavelength imaging in photonic crystals[J].Phys. Rev.B,2003,68(4):045115-1-045115-15.
[16]NOTOMI M.Theory of light propagation in strongly modulated photonic crystals:Refractionlike behavior in the vicinity of the photonic band gap[J].Phys.Rev.B,2000,62(16):10696-10705.
[17]CUBUKCU E,AYDIN K,OZBAY E,et al.Electromagnetic waves:Negative refraction by photonic crystals[[J]. Nature(London),2003,423(6940):604-605.
[18]KOSAKA H,KAWASHIMA T,TOMITA A,et al.Superprism phenomena in photonic crystals[J].Phys.Rev. B,1998,58(16):R10096-R10099.
[19]HU X H,SHEN Y F,LIU X H,et al.Superlensing effect in liquid surface waves[J].Phys.Rev.E,2004,69(3):030201.
[20]XIA F,YUN M J,LIU M L,et al.Negative refraction and subwavelength imaging in a hexagonal two-dimensional annular photonic crystal[J].J.Appl.Phys.,2013,113(1):013109.
[21]KE M Z,LIU Z Y,QIU C Y,et al.Negative-refraction imaging with two-dimensional phononic crystals[J].Phys. Rev.B,2005,72(6):064306-1-064306-5.
[22]LIANG F,LIU X P,LU M H,et al.Acoustic backwardwave negative refractions in the second band of a sonic crystal[J].Phys.Rev.Lett.,2006,96(1):014301.
[23]CROENNE C,MANGA E D,MORVAN B,et al.Negative refraction of longitudinal waves in a two-dimensional solid-solid phononic crystal[J].Phys.Rev.B,2011,83(5):054301.
[24]HLADKY-HENNION A C,VASSEUR J O,HAW G,et al.Negative refraction of acoustic waves using a foam-like metallic structure[J].Appl.Phys.Lett.,2013,102(14):144103-1-144103-4.
[25]ZHOU X M,ASSOUAR M B,OUDICH M.Acoustic superfocusing by solid phononic crystals[J].Appl.Phys. Lett.,2014,105(23):233506.
[26]ZHANG X D,LIU Z Y.Negative refraction of acoustic waves in two-dimensional phononic crystals[J].Appl. Phys.Lett.,2004,85(2):341-343.
[27]QIU C Y,ZHANG X D,LIU Z Y.Far-field imaging of acoustic waves by a two-dimensional sonic crystal[J]. Phys.Rev.B,2005,71(5):054302.
[28]LI J,LIU Z Y,QIU C Y.Negative refraction imaging of acoustic waves by a two-dimensional three-component phononic crystal[J].Phys.Rev.B,2006,73(5):054302-1-054302-5.
[29]HE Z J,LI X C,MEI J,et al.Improving imaging resolution of a phononic crystal lens by employing acoustic surface waves[J].J.Appl.Phys.,2009,106(2):026105-1-026105-3.
[30]LI J,LIU Z Y,QIU C Y.Negative refraction imaging of solid acoustic waves by two-dimensional threecomponent phononic crystal[J].Phys.Lett.A,2008,372(21):3861-3867.
Negative refraction and imaging of two-dimensional phononic crystal with honeycomb-lattice
LIN Jian1,2WU Fugen1YAO Yuanwei2ZHANG Xin2
(1 Department of Experiment Education,Guangdong University of Technology,Guangzhou 510006,China)
(2 Department of Physics and Optoelectronic Engineering,Guangdong University of Technology,Guangzhou 510006,China)
To get a superior imaging resolution,a flat len of two-dimensional phononic crystal(PC)with honeycomb-lattice,which is composed of water/mercury,was studied by finite-element method.The band structure and equifrequency contour(EFC)of the PC were calculated and the Gaussian beam was used to demonstrate the negative refraction effects of the PC len.It is found that the effective index of-1 could be obtained by simulation with a point source.As contrasted to square-lattice and triangular-lattice with these same materials,the better effects of imaging and a dominant resolution can be gotten with honeycomblattice.In order to improve the imaging resolution,a new model based on the old one was presented with a subwavelength imaging resolution of 0.37λ.
Phononic crystal,Negative refraction,Honeycomb-lattice,Imaging
O735
A
1000-310X(2015)06-0533-06
10.11684/j.issn.1000-310X.2015.06.009
2015-06-01收稿;2015-07-30定稿
∗广东省自然科学基金重点项目(S2012020010885),广东省科技计划项目(2012b01010036)
林建(1990-),男,广东湛江人,硕士研究生,研究方向:声子晶体。
E-mail:wufugen@21cn.com

