帆船直线航行比赛最优路径的规划设计

王国兴

(福建省帆船帆板运动管理中心 福建厦门 363021)

帆船运动是水上运动的重要项目之一,帆船在行驶中和机动船的动力源不同,它主要是依靠风对帆产生的作用进而推动船前进的。帆船项目是运动员驾驶帆船在一定的距离内比试航速的运动。结合海洋信息制定最优路径是帆船比赛取得最终胜利的关键。当前,普通船舶的气象导航系统已经逐渐的完善,但是帆船在海上航行中受海浪、海风和海流的影响比较大,因此，在规定的航程和航道宽度内制定航行时间最短的最优路径要比普通的船舶困难许多。

1 帆船航行比赛中的主要特征

1.1 帆船运动员的体能因素

帆船运动对运动员的身体素质要求是全面的,主要要求的内容有运动员的基础性耐力,相对强大的力量,身体核心的力量,全身肌肉的协调合作能力还有个人的力量和速度爆发力。帆船运动和其他速度竞技运动不同的是,比赛的速度不是来源于运动员而是海风,体能在运动中主要用来对风的控制。航速的是人体对风能利用率的体现,运动员只有利用好风,掌握海风的变化特点才能得到较好的航速。除了以上复杂了各项要求以外,帆船比赛的航程一般比较长,比赛时间也很长,这样对比赛选手的专业综合素质和能力是有比较高的要求的。

1.2 复杂的比赛技术

帆船选手在比赛中要根据不同区域内的实际情况,例如:海风风向、梯度风的形状以及运动员自身的身体情况等对自身的技术等进行适当的控制和调整,争取在比赛中以最短的时间完成比赛规定的路程。在整个比赛过程中帆船选手不可能单一的按照某一个操控技术完成整个比赛航程,在帆船运动员的灵活掌握下根据实际情况的变化对帆船进行掌控。

1.3 强大的心理素质和较高的智力要求

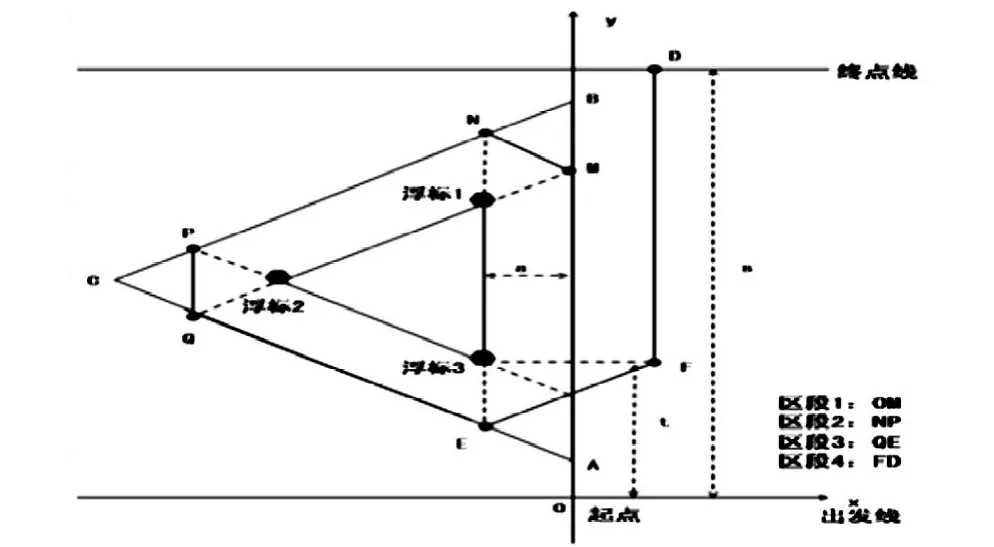
图1

帆船项目是一个涉及了多种学科和知识类型的需要运动员具备高智商的运动,运动员除了要有强大的知识能力和素质,帆船项目看似是各个运动员之间的竞赛,其实在比赛中运动员需要面对的自然环境变化的考验要远远强于比赛中对手给予的压力,因此,帆船运动员还要具备良好的心理素质,方便其随时面对各种自然变化,在面对各种惊险心中不起一丝波澜,要有强大的心理素质调节能力和顽强的意志力以及高速划行的感知力。帆船的动力性能涉及到海上各种气象的影响,此外还要掌握海上救生、快速航行等问题,帆船比赛的规则十分的多。综上可知,帆船运动对运动员的素质要求是十分的高的。

1.4 复杂的影响因素

帆船比赛是在海上,海上的气候条件是随时有肯能发生变化的,极有可能会出现无法正常举行比赛的变化,赛事的时间也可能会被重新安排。比赛成绩极易受到天气的影响,比赛很有可能由于外部因素进行十几次的调整,运动员如何在长时间的跨度下进行自我调节和控制,选手的稳定性在比赛中也是十分重要的,运动员的体能条件和相关训练是比赛取得胜利的基本保障,比赛最终能够取得胜利的关键在于运动员可以对比赛中出现的各种因素进行及时合理的调节。

2 项目特征的相互联系

帆船比赛的是对运动员的体能、知识、技能等许多方面的综合,但是整个比赛最为关键的还是速度。下面对帆船项目取胜的关键规律进行分析和介绍。

2.1 技术的施展要以运动员的体能为前提

一般帆船比赛的赛程和时间都比较长,运动员在长期的运动环境中需要强大心肺活量,比如:在帆船球型帆的升降操作中,为了在比赛中抢占有力的先机,获得更快的速度,升降球型帆技术在帆船比赛中获得了十分广泛的使用,相应的对选手的体能要求也越来越高。良好且全面的体能是帆船运动员实现技术的正常发挥,心智能力的正常体现,达到最佳运动竞技状态的保证和前提。

2.2 技术是体能展现的载体

运动员的比赛技术是非常重要的,要求帆船运动员掌握综合风向、海洋流等多方因素,将体能在技术中达到最佳状态,在运动过程中有效的运用运动技巧提升帆船的速度,最大的节省身体能量的消耗,以最适宜的状态进行比赛。一旦,操作的技术不熟练导致运动员对洋流涌浪的方式判断发生错误,致使航线失去原来的有力位置,导致比赛失败。在训练中养成扎实、专业并且灵活度的技巧可以更好的帮助运动在比赛中更好地发挥自己的体能效应。

2.3 智力能力的重要性

在比赛中除了要有顽强的拼搏奋进精神,同时还要对天气的变化具有预知的能力,综合性的准确判断力、果敢的决策力;并且头脑的思路要清晰、记忆力要强,在遇到不同的状况时要在短时间内迅速的做出正确的判断;敏捷、精确、果断的技术随机应变能力;一心一意、心无杂念的专注力。只有这样帆船运动员才能摒弃其他全面的实现心智能力的发挥。

3 帆船直线航行比赛的优化方案

3.1 基本航线模型的建立

对基本航行的模型进行建立,主要的赛场形式是以三个浮标为正三角形顶点的模式,比赛开始后,运动员以直线运动的方式先到达最短的浮标,随后再依次绕行其他两个浮标,在绕行浮标的圈数达到比赛的要求后,最后以直线航行的方式行驶至终点。

3.2 全程最优路线

现在将整个路线分为几个主要的路段,并且对整个赛程进行分段优化:(1)起点到1号浮标;(2)1号浮标到2号浮标;(3)2号浮标到3号浮标;(4)3号浮标到终点。各个区段的拐弯处实行单独优化。

在帆船的航行过程中,第1区段的中心位置线是OM,第2区段中心位置线是NP,依次第3、4区段中心位置线分别是QE、FD。以上四段中心线也同时是航行路径中的最短路径。其中△ABC是正三角形。比赛中运动员可以驾驶帆船沿最短路径以直线运动的方式从M运动至N,P运动至Q,从区段3到区段4的相应优化拐弯方法和前四段一样,区段2、3、4区段3向区段4的转弯处需要实行坐标的平移和旋转后得到虚拟的各区段坐标。在各区段的优化中风向角 θ、海浪风向角和海流方向角 φ也要发生转换,成为各段虚拟坐标系的角度,进而确定各区段的最短航程L,最短路径通过最优规划方案分析得出,随后在坐标系的位置变换中变换航程坐标系中的坐标。

3.3 不同区段的优化

在帆船比赛的起始点中划分n个区段,n的值主要是航行的距离和航行的实践经验来确定的,并用评价函数的线性加权法在每个区间中对航行的目标进行管理。在k区间内的Pkj航行方向上帆船航向的决策评价函数EVkj定义成:

式中,Tkj=L/(n·Vkj)为整个k区间的航行时间;Vkj为帆船方向运动时在最短的路径方向上的分速度Vkj=Vy=VBcosψ;(Xkj,Ykj)是帆船在k区间到k+1区间交界点Pkj的坐标;Z(Xkj,Ykj)为帆船运动到(Xkj,Ykj)位置的隶属函数,指的是距离目标点的大小; τ2为加权系数, τ1≥0, τ2≥0,并且 τ1、 τ2的和是1; η为负值,以上函数需要满足的条件是帆船在从这一目标航行至下一目标的过程中不能超过航道的宽度,对航道决策条件的约束函数描述为:

上面的式子中,f0=0,k=1,2….,n0Xkj。 Xkj表示k区间和k+1区间的交界点Pkj横坐标的值;M为航道宽度。

无约束航向决策综合评价函数:

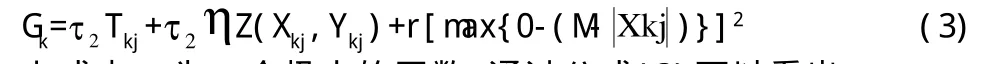
上式中,r为一个极大的正数。通过公式(3)可以看出:

(1)当(M-Xkj)0≥时,max{0-(M-Xkj)}=0对可行点不进行惩罚。

(2)当(M-Xkj)<0时,max{0-(M-Xkj)}-(M-Xkj)对不可行点进行大的惩罚。

在以上优化的整体方案中计算需要注意的主要内容有以下几个方面。

(1)种群的初始化要求,在不同要求的帆船比赛中,根据不同的比赛规定和情况,将帆船航道的边界条件展开相应的变化,在符合边界约束条件的情况下均匀选择m个量当做初始种群。

(2)适当选择函数,文中的公式(3)是航向决策综合评价函数。

(3)变异算子,初始种群是附带,其中要采用的自适应变异机制进行相应的变异。

(4)算子的选择,每一个父子在经历变异后悔产生子个体,并且子个体和父个体的数量是一致的。

(5)收敛判断,最终经过试探和应用,最大的迭代次数被确定。

4 结语

综上可知,帆船直线航行比赛影响的因素比较多。该文对直线航行的路径进行规划得到最优路径,该结果可以在比赛中具有一定参考价值。

[1]邢惠丽,胡西厚,葛艳.帆船比赛航行路径优化与仿真[J].计算机工程与应用,2010(27):245-248.

[2]葛艳,孟庆春,闫传军,等.帆船行驶最优控制策略分析[C]//.中国自动化学会控制理论专业委员会.第二十三届中国控制会议论文集(上册).中国自动化学会控制理论专业委员会.2004.

[3]杨柠语.必读的帆船赛事小知识[J].海洋世界,2013（1）：22-23.

[4]韩海燕,肖一晨.你的小帆船,我的大梦想——2015年青岛市青少年暑期帆船训练活动拉开大幕[J].走向世界,2015（34）：72-75.

[5]徐海亮,梅泽元.海军军事三项赛帆船团体比赛项目特征及最优航行路径规划研究[J].体育世界（下旬刊),2013(10）:57-59.