斜坡上波浪破碎与越浪非静压数值模拟

张 娜，邹国良

(1. 天津城建大学 土木工程学院，天津 300384; 2. 南京水利科学研究院，江苏 南京 210024)

斜坡上波浪破碎与越浪非静压数值模拟

张 娜1，邹国良2

(1. 天津城建大学 土木工程学院，天津 300384; 2. 南京水利科学研究院，江苏 南京 210024)

为合理确定防浪建筑物的越浪量，基于含非静水压力梯度项的非线性浅水方程建立了近岸波浪越浪数值模型。通过采用域内造波、消波并结合波前静压假定的破碎模型，模拟了规则波和不规则波在斜坡上的波浪传播变形，并在此基础上进行了越浪量数值计算。数值计算结果与物理模型实验结果表明，非静压模型可合理地描述波浪破碎点位置、破碎后的波高、增减水以及斜坡上的堤后越浪量。数值模型具有较高的计算精度和计算效率，可为实际工程防浪建筑物越浪以及堤顶高程的设计提供一种新的数值研究手段。

非静压；海堤；波浪破碎；越浪量；数值模拟

修筑堤防、护岸是沿海地区抵御风暴潮灾害的主要工程设施。如果波浪水体大量越过堤顶，就可能对堤后结构造成破坏。因此，寻求一种高效高精度的数值方法模拟波浪在斜坡上的传播变形及越浪，对实际工程合理确定海堤护岸堤顶高程具有十分重要的意义，可为我国海堤的合理设计提供科学依据。

越浪过程包括了波浪在斜坡上的爬高、破碎等复杂的波面变形，以往研究大多采用物理模型实验的方法，并在大量实测数据的基础上提出估算海堤越浪量的经验公式[1-3]，为数学模型的开发提供了宝贵的验证资料。

数值模拟是海堤护岸越浪量的一种重要研究方法。目前数值计算越浪的平面二维模型主要是沿水深积分的模型(如缓坡方程模型和Boussinesq 方程模型等)。二维模型虽然能够较好地模拟不同波浪变形[4-9]，但在描述地形变化剧烈、短周期波、大密度梯度等动压力过程的快速变化时仍存在不足。近些年，在波浪与建筑物相互作用、波浪变形数值模拟中发展较快的三维数值模型主要有无网格SPH粒子方法[10]、基于VOF方法求解自由面的雷诺时均N-S方程(RANS)[11-15]等。这些方法适合模拟波浪翻卷、破碎等具有大变形和运动交界面的强非线性自由表面流动问题，已被用于海堤的越浪模拟，但其计算量大，计算效率低，制约了其在实际工程中的广泛应用。

近年来，采用水位函数法求解自由面的三维非静压波浪模型得到了较快发展。基于非静压模型SWASH模拟实验室尺度的低频波在斜坡和浅滩上的传播，并与水槽实验进行对比发现，不仅波高与周期较为吻合，还能有效模拟低频波的破碎现象[16]。基于Godunov离散格式的三维非静压波浪模型NHWAVE能够较好地模拟波浪的反射，绕射和破碎[17]。通过引入改进的k-ε模型和随时间变化的孔隙率系数，NHWAVE还能模拟三维孤立波与多孔结构的相互作用、渗透结构周围的流场及低频波的传播[18-19]。基于有限元开发的沿深度积分的非静压模型CCHE2D-NHWAVE被用于近岸波浪破碎、越浪量及植被消波的数值模拟[20-21]。

基于N-S方程的非静压波-流模型SWASH近年开始逐渐应用于近岸波浪变形及波浪与建筑物相互作用的描述[16, 22-24]。SWASH最早是由Delft大学开发的，其开源程序可通过http://swash.sourceforge.net免费获取[25]。近期针对模型开展了一系列的研究，如通过在连续性方程中添加质量源项进行域内源造波，在非静压模型中实现无反射造波[26]；将基于求解相位平均的波作用谱模型和求解相位的非静压波浪模型进行嵌套，合理描述波浪从大范围区域向小范围区域的传播变形等[27]。SWASH通过求解含非静压项的非线性浅水方程来模拟波浪的传播变形，在垂向往往只需要2～3层[28]即可较好地描述强非线性和强色散性波，使得近岸波浪变形的模拟既能满足精度要求，又具有较高的计算效率，对于实际工程具有很大的应用潜力。

目前基于非静压波浪模型模拟越浪的研究较少[22]。为此，本文应用非静压SWASH波浪模型模拟规则波和不规则波作用下的波浪在斜坡上的传播变形(包含了破碎过程)与越浪，并与物理模型实验结果进行对比，检验非静压波浪模型SWASH的模拟精度，同时也为越浪的数值模拟提供一种新的计算方法。

1 数值模拟方法

1.1 非静压波浪模型的控制方程及边界条件

本文的主要工作是在垂向二维的开源非静压波浪模型SWASH基础上进行，该模型控制方程为包含非静压项的浅水方程，其垂向二维的控制方程为：

式中：t表示时间，x是水平坐标，u是x向深度平均的流速，ws和wb分别是表层和底层z方向上的流速，ζ是自由表面高程，d是静水深，H是总水深，qb是底部非静压，g是重力加速度，Cf是无量纲底部摩擦系数，vt是涡粘系数。

在自由表面处忽略表面张应力，压力边界条件为：

底部边界条件为：

造波边界采用域内源造波[26]并结合改进的海绵层消波方法进行数值消波。

1.2 数值方法

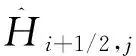
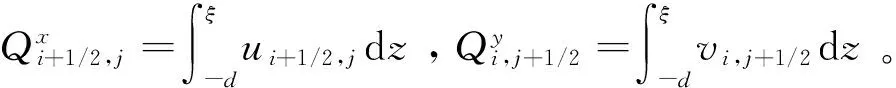
图1 计算网格划分示意Fig. 1 Diagram of computational grid

图2 交错网格变量布置方式Fig. 2 Arrangement of the unknowns with a staggered grid system

非静压模型采用分步法并结合压力校正法求解非静压-速度耦合方程。时间积分采用变时间步长的显格式，具体的方程离散及数值计算方法详见文献[22]。

1.3 波浪破碎模型

波浪从深水向浅水传播的过程中，其非线性影响逐渐增强。伴随着波形的变陡，水质点的垂向速度梯度增大，波峰处水质点速度接近波浪相速度，而波谷处水质点速度相对较小，当波峰处的水质点水平速度等于波浪传播的相速度时，波形不能保持稳定，波浪发生破碎，破碎波形成后尽管波前垂向速度梯度仍然较大，但非静压梯度的影响，尤其是在沿水深积分形式的动量方程中的影响变得较小[28]。因此，波浪在发生破碎时，采用波前静压假定方法将非静压模型转化为可较好描述破波带内波浪传播守恒的非线性静压浅水方程，可降低模型在模拟波浪破碎时的垂向网格数量。Smit 等[23]提出当网格点的垂向速度满足式(10)或者其临近网格的垂向速度满足式(11)时(β<α)即认为波浪破碎，该网格的非静压设置为零，只进行静压计算；当破碎波波峰离开该网格点，即垂向速度满足式(12)时，重新进行非静压计算。

式中：c为波速，α和β分别为与破碎波形态有关的系数。

本文旨在探讨垂向网格较粗即分层较少时利用非静压波浪模型模拟波浪破碎，且在波浪破碎时将模型转化为静压非线性浅水方程模型，因此可通过引入紊动模型的方法来模拟波浪破碎引起的能量损耗。紊动模型的关键在于合理确定紊动粘滞系数，SWASH模型中波浪破碎的粘滞系数采用的是类似于Zelt[29]提出的混合长度模型，即认为粘滞系数与速度梯度以及混合长度有关：

式中：lmix为混合长度，与当地的波高成正比，比例系数为1[23]。

2 模拟结果

斜坡上越浪的模拟首先需要数学模型能准确地模拟波高、破碎点、增减水等，为此采用物理模型实验对数学模型在规则波和不规则波作用下的波浪传播变形进行验证。在此基础上进一步利用物理模型实验对规则波和不规则波作用下的越浪数值模拟进行验证。

2.1 波浪在斜坡上传播变形的数值模拟分析

1)规则波作用下波浪变形数值模拟及验证

规则波作用下波浪传播变形的数值模拟基于Ting的崩破波模型实验[5]。该模型为一个40 m长的波浪水槽，造波位置的静水深为0.4 m，距离造波板24.75 m处有一段1∶10的陡坡，由坡底0.4 m水深过渡到坡脚处静水深为0.38 m，水槽末端设置一段1∶35的斜坡延伸至陆地，坡顶露出水面0.05 m，如图3所示。入射波高为0.125 m，平均周期为2.0 s，沿程布置了21个传感器，传感器坐标值如表1所示(坡脚的静水面位置为坐标轴原点，坡脚位置水平方向向右为x轴正向，静水面竖直向上为y轴正向)。

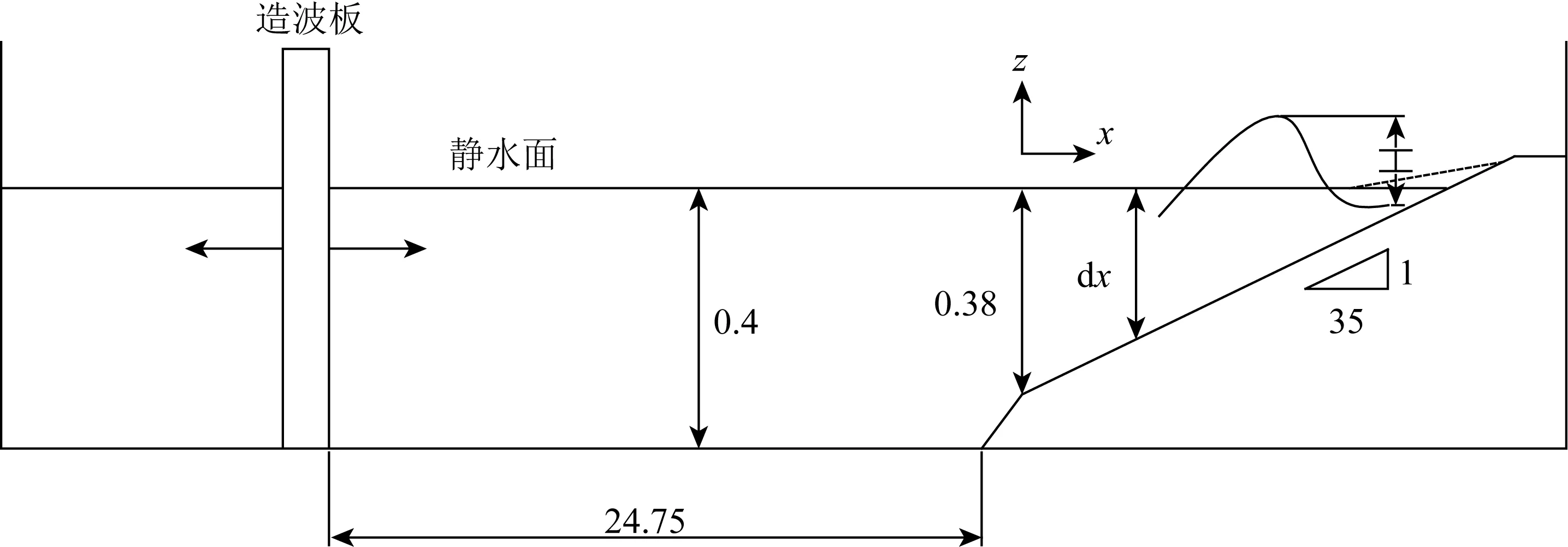
图3 实验布置(单位：m)Fig. 3 Experimental setup of regular wave transformation (measurements are in meters)

传感器编号1234567891011X坐标/m-1.45-0.460.541.542.533.524.535.516.016.406.52水深/m0.4000.4000.3640.3350.3070.2780.2490.2210.2060.1940.190传感器编号12131415161718192021X坐标/m7.017.518.028.519.019.499.9810.4910.9911.50水深/m0.1760.1630.1490.1370.1220.1060.0900.0760.0630.049

数学模型的范围与物理模型基本一致，在进行模型参数设置时，水平方向的网格步长为0.05 m，垂向划分了2层(垂向分层由kd值决定，其中k表示波数，d表示水深。当kd<7.0时，垂向划分2层即可满足色散性要求[22])。初始时间步长为0.01 s，计算时间步长会根据CFL数自动调整，最大CFL数设置为0.4。与物理模型实验一致，水槽左端为入射边界，波浪以源函数造波方式给出[26]，模型始末端边界设置各10 m的海绵层，以消除二次反射。由于波浪数值水槽需要额外预留设置海绵层的空间尺度，因此总长度为60 m。模型计算的初始时间步长为0.01 s，取200个波周期进行波高与增减水的统计。

由于波浪破碎参数的选取对模拟结果具有重要影响，为此分别对最大波陡参数α(0.4～0.8)和波形参数β(0.2～0.6)进行波高与增减水的敏感性分析，结果发现，波形参数β=0.2不变，当α从0.6减小至0.4时，波浪初始耗散滞后，当α从0.6增大至0.8时，波浪初始耗散提前。波形参数β对于波高及增减水的影响并不如最大波陡参数α的作用明显，如图4所示。根据敏感性分析实验可知，最大波陡参数α设为0.8，波形参数β设为0.2时，表1所示的各传感器位置波高与增减水的计算值与实测值吻合最好。

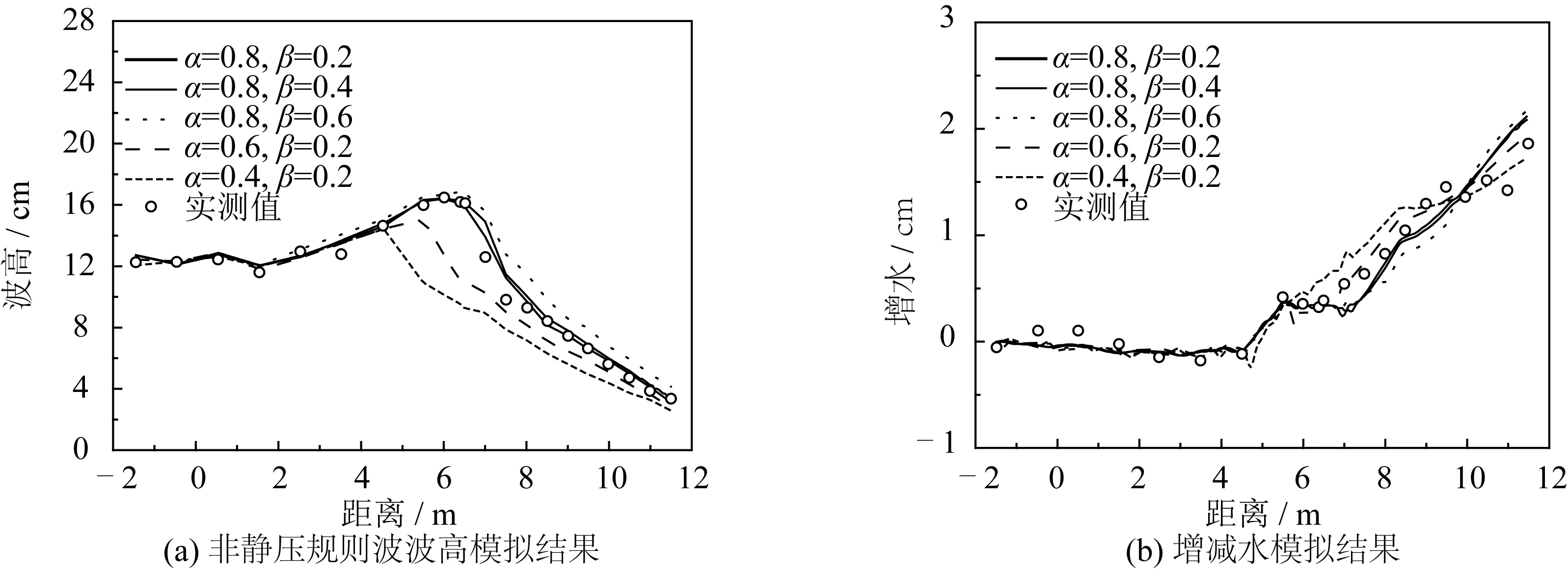
图4 非静压规则波波高模拟结果及增减水模拟结果与实测值对比Fig. 4 Comparison between physical and numerical simulations for the spatial distribution of Hm0 and wave set-up

对采集到的波高数据(α=0.8，β=0.2)进行分析，计算的最大波高值为0.168 m，对应水深为0.203 m，该点增水为0.33 cm；实测值的最大波高为0.165 m，对应水深为0.206 m，该点增水为0.35 cm。计算出的破波点处水深为0.201 m，破碎波高为0.162 m，该点增水0.32 cm；实测值的破波点处水深为0.196 m，破碎波高为0.162 m，该点增水0.32 cm。波浪破碎后继续向近岸传播，该过程中波高和水深比一直保持常数，在0.61左右，在X=11.5 m处，波高与水深比降为0.38，规则波作用下的数学模型与物理模型实验结果吻合较好。

2)不规则波作用下的波浪变形数值模拟及验证

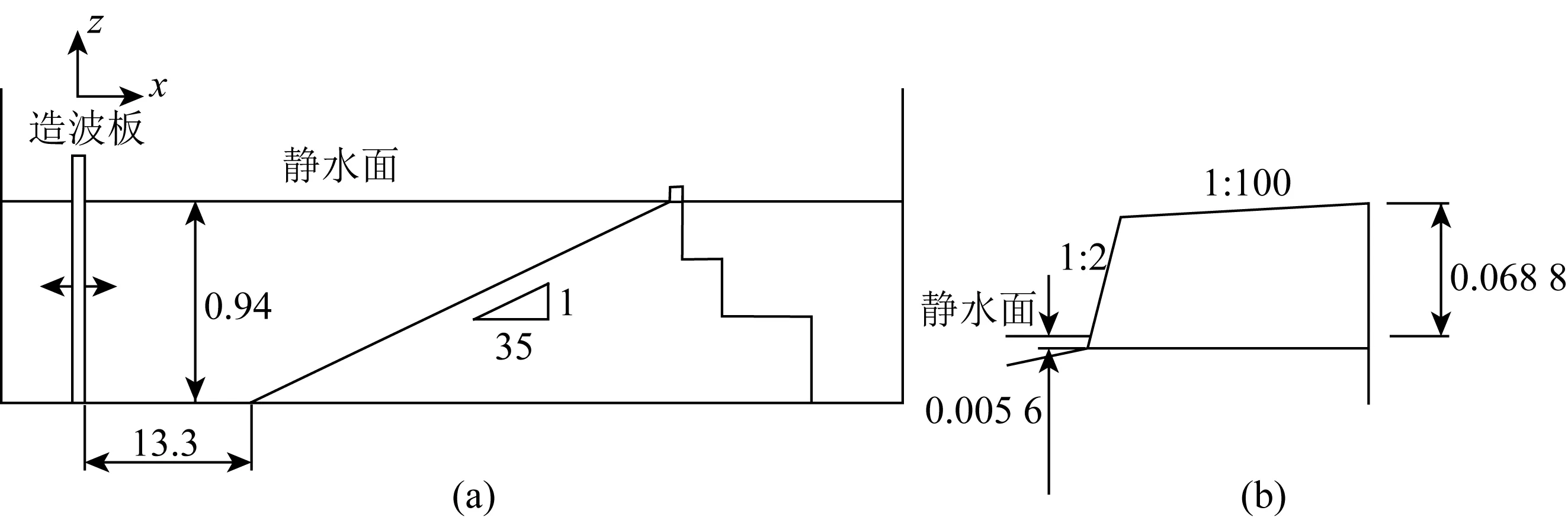
图5 实验布置(其中(b)为海堤局部放大，单位:m)Fig. 5 Experimental setup of irregular wave transformation and wave overtopping (measurements are in meters)

传感器编号123456X坐标/m12.030.036.041.044.846.0水深/m0.94000.46860.29540.15110.04140.0056

波浪数值水槽长度为70 m，与物理模型实验一致，网格步长为0.04 m，垂向划分2层。初始时间步长为0.005 s，模拟时间与物理模型实验一致，为40 min，取769个波周期进行波高与增减水的统计。底摩阻系数取0.01，实验时，水槽两端设置了10 m的海绵层，以消除波浪反射的影响。波高与增减水的数物模结果对比如图6所示，能量谱模拟结果与物模结果对比见图7。

图6 非静压不规则波波高模拟结果及增减水模拟结果与实测值对比Fig. 6 Comparison between physical and numerical simulations for the spatial distribution of Hm0 and wave set-up

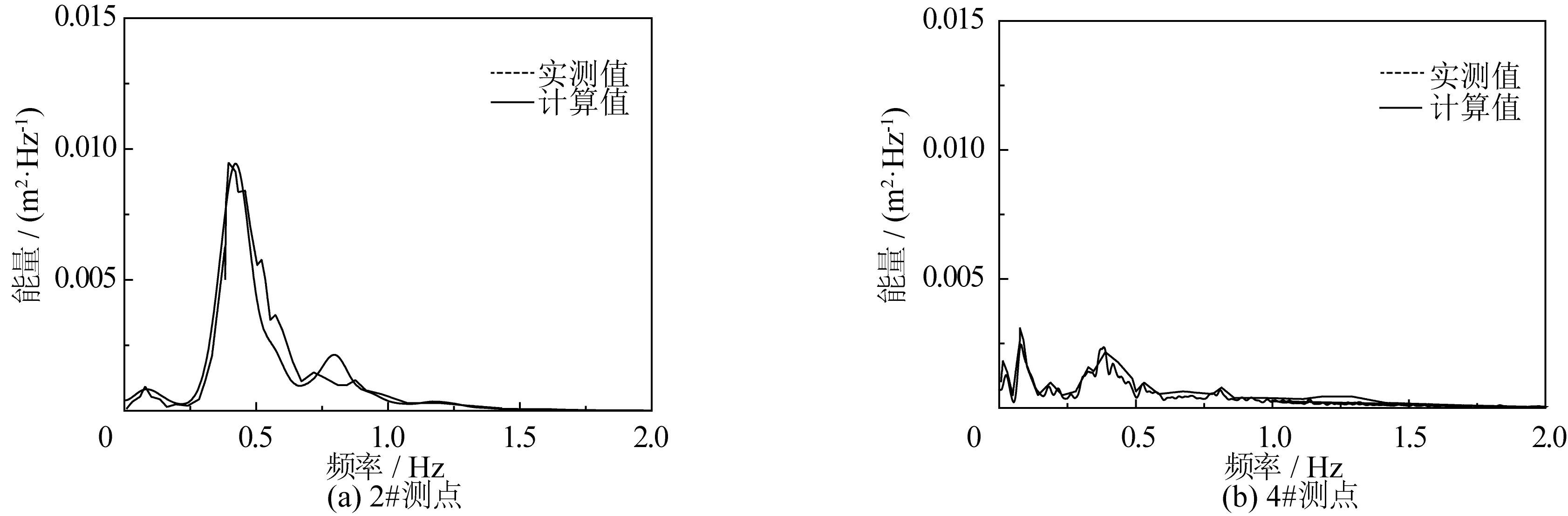
图7 2#测点及4#测点不规则波能量谱模拟结果与实测值对比Fig. 7 Comparison between physical and numerical simulations for wave energy spectrum at station 2 and station 4

根据实验结果可知，不规则波从外海传至近岸海堤的过程中，计算值的波高在2#测点位置处达到最大，最大波高为0.199 m，减水为-0.252 m；物模测量的最大波高为0.195 m，也是在2#测点位置达到最大，减水为-0.276 m，数物模对比的谱能量分布如图7(a)所示。在4#测点位置处，计算值的波高发生破碎，破碎波高为0.122 m，增水为0.295 m，波高与水深之比为0.81；物模测量的破碎波高为0.134 m，增水为0.165 m，波高与水深之比为0.88，图7(b)显示了波浪破碎后的双峰谱能量分布(数模与物模对比图)。总体来说，不规则波作用下的数学模型与物理模型实验结果吻合较好。

2.2 波浪越浪的数值模拟分析

平均越浪量qa可根据越浪水舌厚度h(t)与堤顶末端的水层流速u(t)计算。瞬时越浪量qi(t)与平均越浪量qa的关系可由下式表示：

式中：ts和te分别代表测量越浪量的开始和结束时间。

1)规则波作用下的越浪数值模拟及验证

规则波作用下的越浪数值模拟是基于张九山的物理模型实验[13]。水槽长60 m，宽0.8 m，高1.2 m，造波机至缓坡坡脚位置为一段长度为15 m的平底，静水深为0.65 m，缓坡的坡度为1∶40，缓坡坡顶位置的静水深为0.45 m，之后通过一段长度为7 m的平底过渡到斜坡堤堤脚。从斜坡堤堤脚通过一段1∶3的斜坡过渡到斜坡堤堤顶，斜坡的水平长度为1.5 m，斜坡堤顶部高出静水面0.05 m。在斜坡堤堤顶设置一个直立式胸墙，胸墙顶高出静水面0.125 m，实验布置如图8所示。规则波入射波高为0.132 m，平均周期1.357 s。

图8 实验布置(单位：m)Fig. 8 Experimental setup of regular wave overtopping (measurements are in meters)

数学模型的范围与物理模型实验基本一致，在进行SWASH模型参数设置时，水平方向的网格步长为0.05 m，垂向划分了两层。初始时间步长为0.01 s。与物理模型实验一致，水槽左端为入射边界，波浪以源函数造波方式给出[26]，水槽两端各设置了7.2 m的海绵层，以消除波浪的二次反射。堤脚处波面高程随时间变化历时曲线的数物模结果对比如图9所示，数模模拟的规则波单宽瞬时越浪量的历时曲线如图10所示。图11为堤顶末端的越浪水舌厚度和水层速度随时间变化曲线。

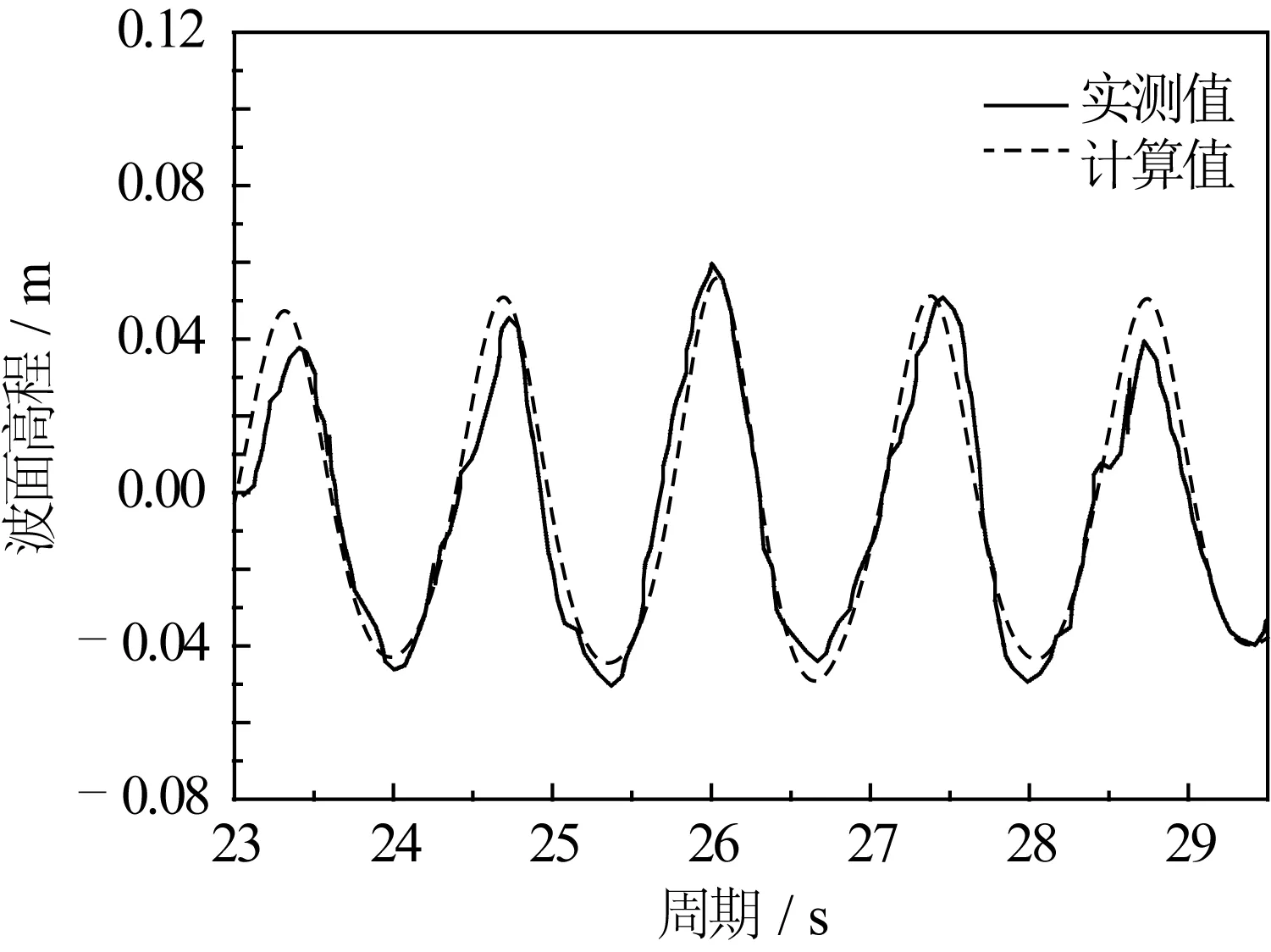
图9 堤脚处波面高程随时间变化历时曲线数物模结果对比Fig. 9 Comparison between physical and numerical simulations for time series of free-surface

图10 规则波单宽瞬时越浪量的时间过程线Fig. 10 Time series of instantaneous wave overtopping discharge elevations at the toe of the dike

图11 堤顶末端越浪水舌厚度和水层速度随时间变化曲线Fig. 11 Time series of layer thickness and layer speed

根据图9可知，数物模各时刻的波面过程吻合较好。根据数值模拟结果，从第40 s到第60 s的时间段内，最大单宽瞬时越浪量为0.014 m3/m·s，发生在第42.55 s，对应时刻的越浪水舌厚度为0.022 m，堤顶水平流速为0.648 m/s。根据公式(10)对图11中越浪水舌厚度与水层速度相乘即得到图10中的单宽瞬时越浪量，再利用公式(11)对图10中的单宽瞬时越浪量进行面积积分，即求得平均越浪量为qa=1.48×10-3m3/m·s，与物理模型实验测量的平均越浪量qa=1.44×10-3m3/m·s吻合很好。图12为规则波越浪(t=40 s)的数值水槽波面图，计算结果较好地模拟出了堤顶越浪的过程。

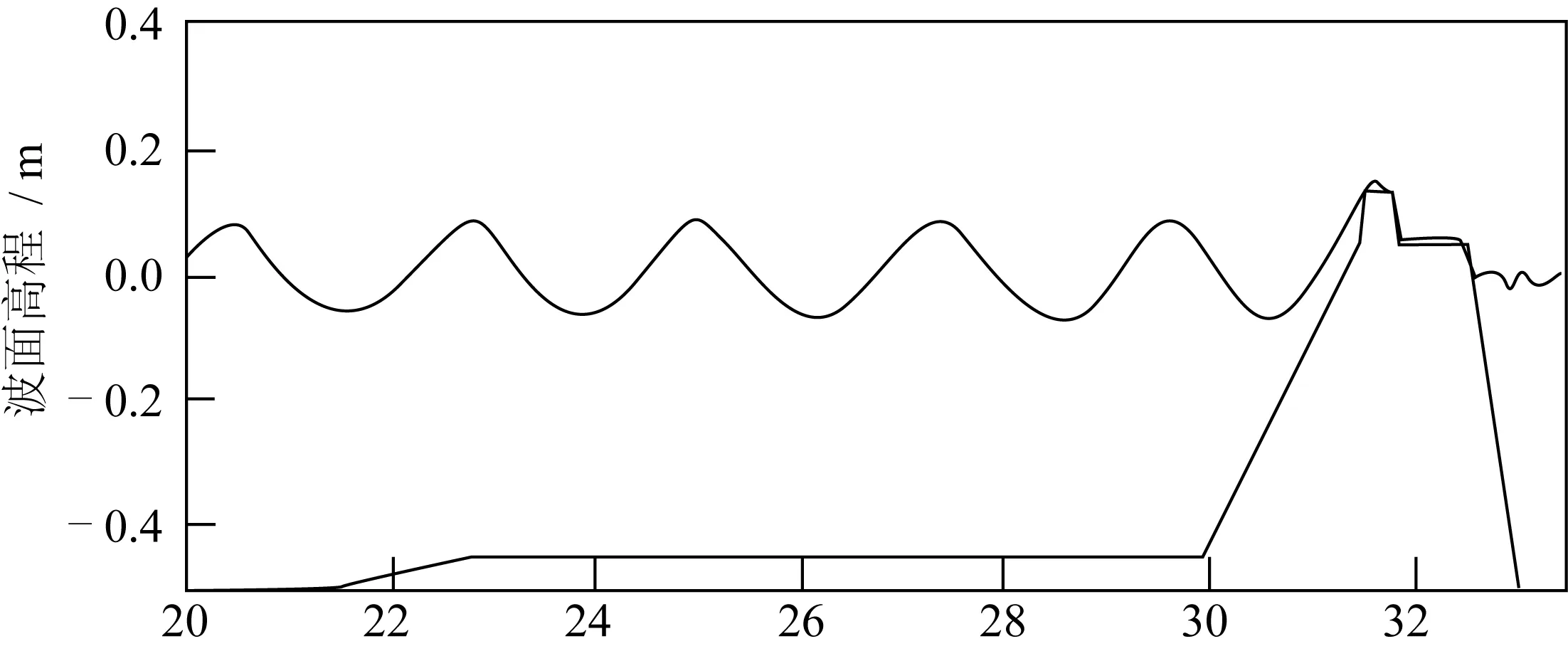
图12 规则波越浪瞬间的数值水槽波面 (t=40 s )Fig. 12 Numerical flume wave surface of instantaneous wave overtopping (t=40 s)

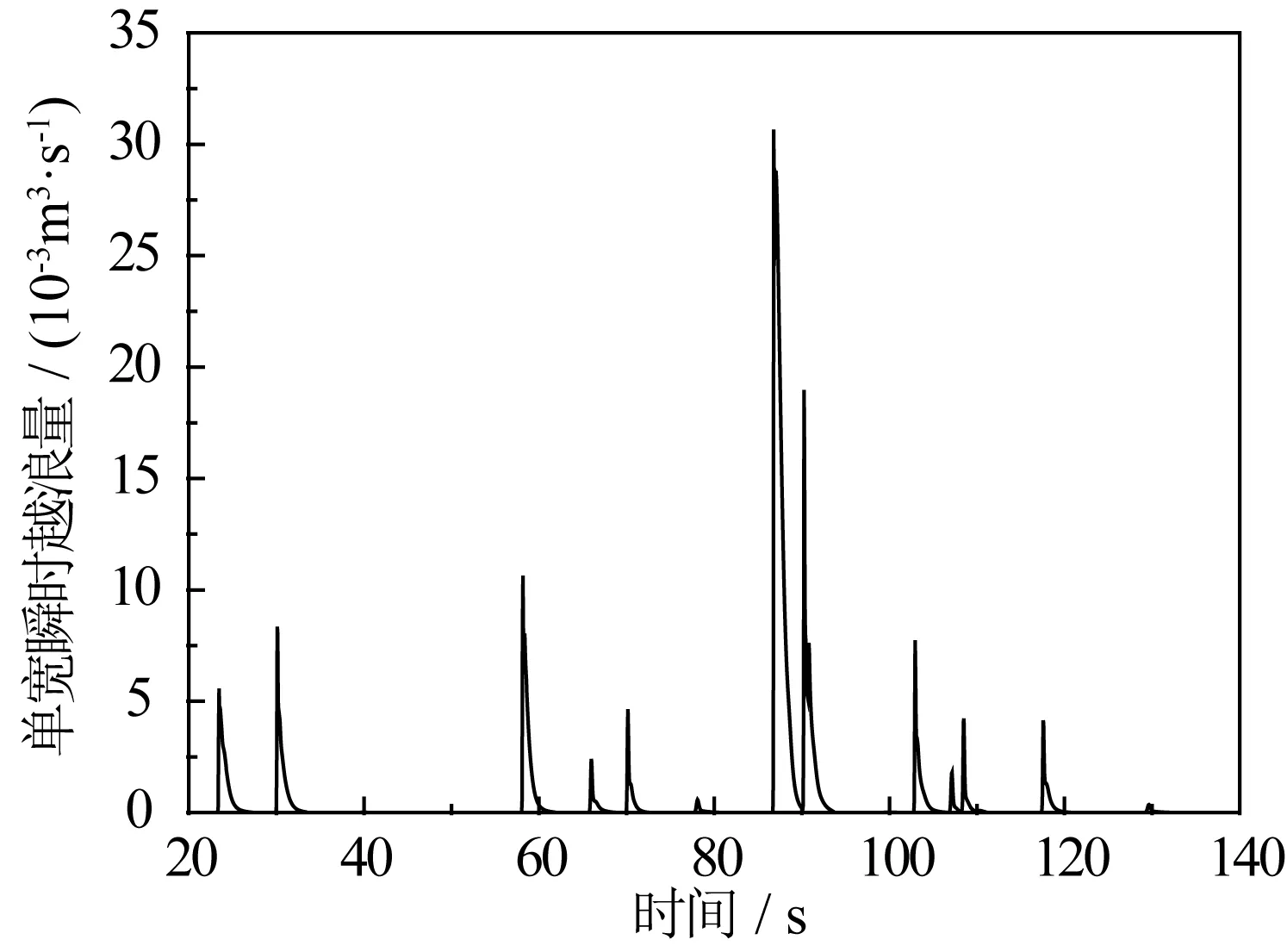
图13 不规则波单宽瞬时越浪量的历时曲线Fig. 13 Instantaneous wave overtopping discharge

2)不规则波作用下的越浪数值模拟及验证

采用Suzuki不规则波作用下越浪物理模型实验对数学模型进行验证[22]，关于波浪在斜坡堤上的传播变形已经在2.1节中进行了论述。图13为数模模拟的不规则波单宽瞬时越浪量的历时曲线，图14分别为堤顶末端的越浪水舌厚度(图14(a))和水层速度(图14(b))。与规则波越浪原理一样，其中单宽瞬时越浪量是由越浪水舌厚度与水层速度的乘积获得。

根据数值模拟结果，从第20 s到第140 s的时间段内，最大单宽瞬时越浪量为0.032 m3/m·s，发生在第86.8 s，对应时刻的越浪水舌厚度为0.020 m，堤顶水平流速为1.592 m/s。利用公式(11)对图12中的单宽瞬时越浪量进行面积积分，即求得平均越浪量为qa=0.56×10-3m3/m·s，与物理模型实验测量的平均越浪量qa=0.58×10-3m3/m·s吻合很好。图15为不规则波越浪(t=58 s)的数值水槽波面图。

图14 堤顶末端越浪水舌厚度和水层速度随时间变化曲线Fig. 14 Time series of layer thickness and layer speed

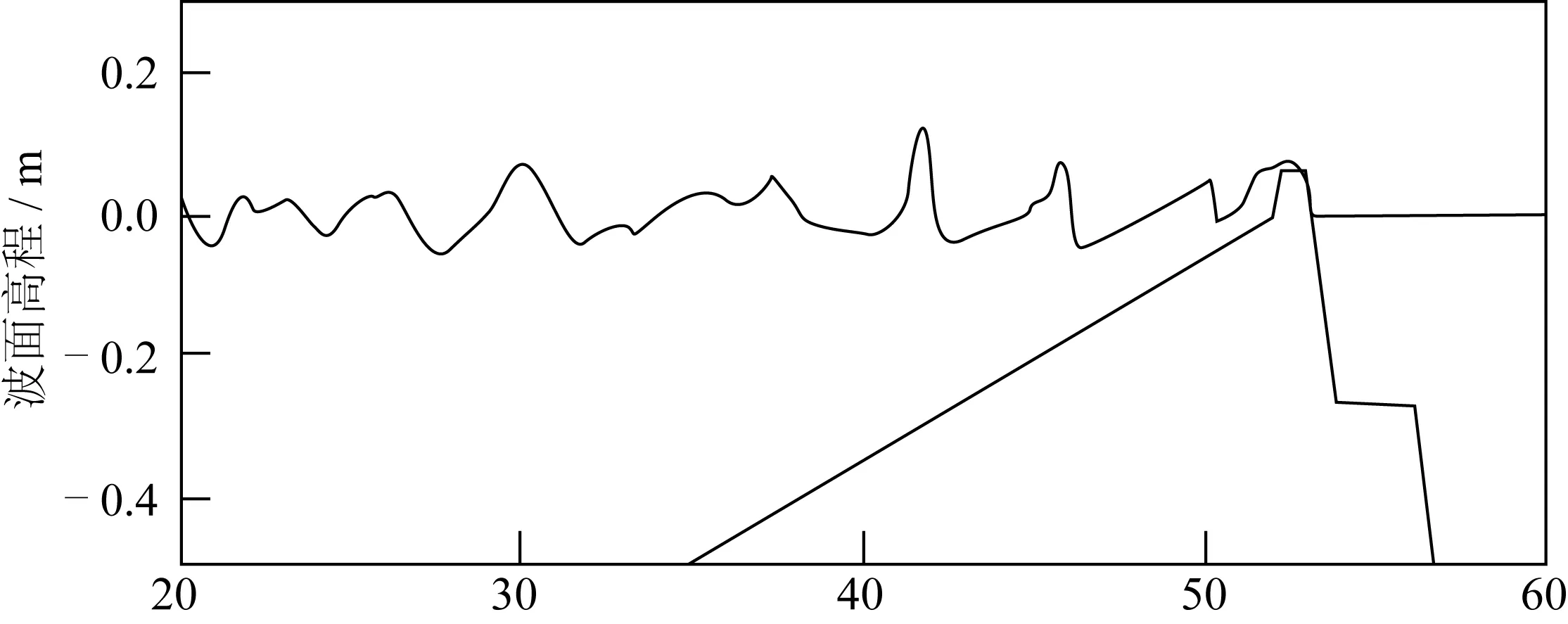
图15 不规则波越浪瞬间的数值水槽波面(t=58 s)Fig. 15 Numerical flume wave surface of instantaneous wave overtopping (t=58 s)

3 结 语

基于非静压模型SWASH建立了波浪数值水槽，利用域内源造波和海绵层消波方法对规则波和不规则波作用下的波浪在斜坡上的传播变形与越浪过程进行了模拟。通过与物理模型实测数据的对比，结果表明，非静压模型SWASH对于模拟波浪传播、破碎、增减水、越浪具有较高的计算精度，此外，垂向只需划分2～3层即可达到该精度要求，表明非静压模型还具有较高的计算效率，对于实际工程具有很大的应用潜力。

[1] 陈国平, 周益人, 琚烈红. 海堤护面形式对波浪爬高和越浪的影响[J]. 水运工程, 2005, 381(10): 28-30. (CHEN Guoping, ZHOU Yiren, JU Liehong. Influence of protective styles of seawall on wave runup and overtopping[J]. Port & Waterway Engineering, 2005, 381(10): 28-30.(in Chinese))

[2] NøRGAARD J Q H, LYKKE ANDERSEN T, BURCHARTH H F. Distribution of individual wave overtopping volumes in shallow water wave conditions[J]. Coastal Engineering, 2014, 83: 15-23.

[3] VAN DER MEER J, BRUCE T. New physical insights and design formulae on wave overtopping at sloping and vertical structures[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2013, doi:10.1061/(ASCE)WW.1943-5460.0000221.

[4] MADSEN P A, SCRENSEN O R. A new form of the Boussinesq equations with improved linear dispersion characteristics: Part 2. A slowly varying bathymetry[J]. Coastal Engineering, 1992, 18: 183-204.

[5] TING F C K, KIRBY J T. Observation of undertow and turbulence in a laboratory surf zone[J]. Coastal Engineering, 1994, 24(1): 51-80.

[6] 王红川, 周正萍. 基于改进缓坡方程的波浪传播数值模拟[J]. 海洋工程, 2013, 31(3): 49-57. (WANG Hongchuan, ZHOU Zhengping. Numerical simulation of wave propagation by modified mild-slope equation[J]. The Ocean Engineering, 2013, 31(3): 49-57.(in Chinese) )

[7] 李绍武, 李春颖, 谷汉斌, 等. 一种改进的近岸波浪破碎数值模型[J]. 水科学进展, 2005, 16(1): 36-41. (LI Shaowu, LI Chunying, GU Hanbin, et al. Improved numerical model for nearshore wave breaking[J]. Advances in Water Science, 2005, 16(1): 36-41.(in Chinese) )

[8] 房克照, 邹志利. 应用二阶完全非线性 Boussinesq 方程模拟破碎波浪[J]. 水科学进展, 2012, 23(1): 96-103. (FANG Kezhao, ZOU Zhili. Simulation of breaking waves using a second-order fully nonlinear Boussinesq-type model[J]. Advances in Water Science, 2012, 23(1): 96-103.(in Chinese) )

[9] 刘忠波, 孙昭晨, 房克照. 波浪在渗透海床上传播的数学模型及其验证[J]. 大连理工大学学报, 2013, 53(3): 417-422. (LIU Zhongbo, SUN Zhaochen, FANG Kezhao. Mathematical model for wave propagation over a porous seabed and its numerical validation[J]. Journal of Dalian University of Technology, 2013, 53(3): 417-422.(in Chinese) )

[10] 任冰, 叶晓文, 高睿, 等. 波浪与多孔介质结构相互作用SPH 模拟[J]. 海洋工程, 2012, 30(2): 46-53. (REN Bing, YE Xiaowen, GAO Rui, et al. SPH modelling of wave interaction with porous structures[J]. The Ocean Engineering, 2012, 30(2): 46-53.(in Chinese) )

[11] THOMAS T G, LESLIE D C. Development of a conservation 3D free surface code[J]. Journal of Hydraulics Research, 1992, 30: 107-115.

[12] PENG Z, ZOU Q P. Spatial distribution of wave overtopping water behind coastal structures[J]. Coastal Engineering, 2011, 58(6): 489-498.

[13] 张九山, 吴卫, 王本龙, 等. 带异形块体海堤越浪的数值模拟[J]. 水动力学研究与进展: A辑, 2006, 21(5): 572-578. (ZHANG Jiushan, WU Wei, WANG Benlong, et al. Numerical simulation of overtopping over seawall with dolos[J]. Journal of Hydrodynamics: A, 2006, 21(5): 572-578.(in Chinese) )

[14] 杨锦凌, 孙大鹏, 吴浩, 等. 斜坡堤波浪爬高和越浪数值模拟[J]. 海洋工程, 2013, 31(2): 45-52. (YANG Jinling, SUN Dapeng, WU Hao, et al. Numerical simulation of wave run-up and overtopping on sloping seawall[J]. The Ocean Engineering, 2013, 31(2): 45-52.(in Chinese) )

[15] 王鹏, 孙大鹏, 吴浩. 海堤上波浪爬高与越浪计算分析[J]. 海洋工程, 2011, 29(4): 97-102. (WANG Peng, SUN Dapeng, WU Hao. Numerical simulation of wave runup and overtopping over seawalls[J]. The Ocean Engineering, 2011, 29(4): 97-102.(in Chinese) )

[16] RIJNSDORP D P, SMIT P B, ZIJLEMA MARCEL. Non-hydrostatic modelling of infragravity waves under laboratory conditions[J]. Coastal Engineering, 2014, 85: 30-42.

[17] MA G, SHI F, KRIBY J T. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes[J]. Ocean Modelling, 2012, 43(44): 22-35.

[18] MA Gangfeng, SHI Fengyan, HSIAO SHIHCHUN, et al. Non-hydrostatic modeling of wave interactions with porous structures[J]. Coastal Engineering, 2014, 91: 84-98.

[19] MA Gangfeng, SU Shifeng, LIU Shuguang, et al. Numerical simulation of infragravity waves in fringing reefs using a shock-capturing non-hydrostatic model[J]. Ocean Engineering, 2014, 85, 54-64.

[20] WEI Zhangping, JIA Yafei. Simulation of nearshore wave processes by a depth-integrated non-hydrostatic finite element model[J]. Coastal Engineering, 2014, 83: 93-107.

[21] WEI Zhangping, JIA Yafei. Non-hydrostatic finite element model for coastal wave processes[J]. Coastal Engineering, 2014, 92: 31-47.

[22] SUZUKI T, VERWAEST T, VEALE W, et al. A numerical study on the effect of beach nourishment on wave overtopping in shallow foreshores[J]. Coastal Engineering Proceedings, 2012, 1(33): 1-13.

[23] SMIT P, ZIJLEMA M, STELLING G. Depth-induced wave breaking in a non-hydrostatic, near-shore wave model[J]. Coastal Engineering, 2013, 76: 1-16.

[24] SMIT PIETER, JANSSEN TIM, HOLTHUIJSEN LEO, et al. Non-hydrostatic modeling of surf zone wave dynamics[J]. Coastal Engineering, 2014, 83: 36-48.

[25] ZIJLEMA M, STELLING G S, SMIT P B. SWASH: an operational public domain code for simulating wave fields and rapidly varied flows in coastal waters[J]. Coastal Engineering, 2011, 580(10), 992-1012.

[26] 邹国良, 张庆河. 非静压波浪模型无反射造波[J]. 海洋工程, 2012, 30(4): 55-61. (ZOU Guoliang, ZHANG Qinghe. Wave generation without re-reflection for non-hydrostatic wave model[J]. The Ocean Engineering, 2012, 30(4): 55-61.(in Chinese) )

[27] 邹国良, 张庆河. 非静压方程与波作用谱模型的波浪传播嵌套模拟[J]. 哈尔滨工程大学学报, 2014, 35(1): 1-6. (ZOU Guoliang, ZHANG Qinghe. Simulation of wave transformation by nesting non-hydrostatic equation with wave action spectrum model[J]. Journal of Harbin Engineering University, 2014, 35(1): 1-6.(in Chinese) )

[28] BATTJES J A, STIVE M J F. Calibration and verification of a dissipation model for random breaking waves[J]. Deep Sea Research Part B. Oceanographic Literature Review, 1986, 33(3): 9159-9167.

[29] ZELT J A. The run-up of nonbreaking and breaking solitary waves[J]. Coastal Engineering, 1991, 15(3): 205-246.

Numerical simulation of wave transformation and overtopping based on non-hydrostatic model

ZHANG Na1, ZOU Guoliang2

(1. School of Civil Engineering, Tianjin Chengjian University, Tianjin 300384, China; 2. Nanjing Hydraulic Research Institute, Nanjing 210024, China)

A wave overtopping numerical model is developed based on the non-linear shallow water equations with non-hydrostatic pressure to reasonably determine the overtopping discharge of the seawall. Wave transformation and wave overtopping discharge on the slope under regular wave and irregular wave are simulated by using internal source generation of waves, wave damping absorber and wave breaking model with hydrostatic front approximation. The results from numerical simulations are compared with physical model data. Good agreement shows that the non-hydrostatic model can reasonably describe the wave breaking location, breaking wave height, wave set-up and wave overtopping discharge. It can be concluded that the non-hydrostatic wave model can provide a new numerical method for practical engineering research of seawall protection with high accuracy and computational efficiency.

non-hydrostatic; seawall; wave breaking; wave overtopping; numerical simulation

TV139.2

A

10.16483/j.issn.1005-9865.2015.02.004

1005-9865(2015)02-0032-10

2014-06-30

天津市自然科学基金资助(14JCYBJC22100)；天津市建交委科技计划项目(2013-8)；国家级大学生创新训练计划项目(201310792017)

张娜(1978-)，女，天津人，博士，高级工程师，主要从事港口、海岸及近海工程研究。E-mail: cheungna@126.com

邹国良。E-mail: glzou@nhri.cn