例谈三角函数图像变换中的易错点

赖建华

（晋江市英林中学 福建晋江 362256）

例谈三角函数图像变换中的易错点

赖建华

（晋江市英林中学 福建晋江 362256）

人教版高中数学必修4，教材在编写函数y=Asin(ωx +ϕ)的图像时，利用计算机技术分别动态地演示了参数ϕ,ω,A对图像的影响，这种化抽象为具体、化静态为动态的方法，可以让学生真实感受到这种变化和影响，学生应该是可以很好理解并掌握好这节内容的，但我发现在具体操作中，学生却很容易犯错。

三角 图像变换 表达式

一、错因分析

针对学生为啥还容易出错，我进行了比较详细的了解和分析，究其原因主要有：1、函数y=sinx的图像变为函数y=Asin(ωx +ϕ)的图像，可以通过改变ϕ,ω,A的变换顺序，达到相同的目的，但中间的变换又有差别，特别是在先ϕ后ω,还是先ω后ϕ时容易出错，以及在ω和A的倍数关系时容易混淆；2、学生在做这种题时，只是利用已学的理论知识解题，不会利用计算机技术辅助解题，即使做错了，他们也发现不了错误；3、最主要原因还是学生对参数ϕ,ω,A对图像的影响，这种影响变换的本质没有理解到位。

二、变换本质

函数y=sinx的图像变为函数y=Asinx （A>0）的图像时，参数A只影响到纵坐标y的倍数，是振幅变换，使得纵坐标y伸长（A>1）或者缩短（00）与单个x同时出现的，是相位变化，构成了x+ϕ的形式，使得y=sinx的图像向左（ϕ>0）或者向右（ϕ<0）移动ϕ个单位；函数y=sinx的图像变为函数y=sinωx(ω＞0)的图像时，参数ω只影响到横坐标x的倍数，是周期变换使得横坐标x伸长（0<ω<1）或者缩短（ω>1）到原来的1倍。ω

三、例题分析

题型1、函数y=Asinx的图像变为函数y=Asin(ωx +ϕ)的图像，在处理参数ϕ,ω对图像的影响时

把函数y=2sinx,x∈R的图像上所有的点做_____________变换；

【典型错误】这种题平时练习比较多的，但学生还是会做错，学生容易在两处出错，错误一：在处理参数ω处，容易错做成ω倍，如向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变）；错误二：如果是

先周期变换后相位变化时，没有提取变量x的系数，容易做成所得图象上各点的横坐标伸长到原来的3倍（纵坐标不变），再图像向左平移个单位。

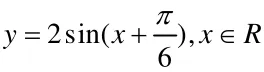
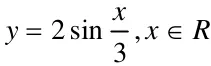
题型2：函数y=sin(ωx +ϕ)的图像变为函数y=Asin(ωx+ϕ)+B的图像，在处理参数A、B对图像的影响时

例题2、（2009年山东卷改编题1）将y=sin2x的图像向左平移个单位，再向上平移1个单位后，纵坐标伸长到原来的3倍（横坐标不变）所得图像的函数表达式为___________。

【典型错误】在此题中A影响的是纵坐标y倍数，是振幅变化，而B是影响图像的上下平移变换，这种题型在教材中没有涉及到，但并不超纲，由于学生平时很少练习到，学生就更容易出错了，易犯错误地方主要有：1、在处理相位变化时，容易把将y=sin2x的图像向左平移个单位后，所得的函数表达式错误做成了y=sin(2x +)；2、在处理先上下平移后纵坐标的振幅变化时，由于对参数A变换的本质认识不到位，做成如将y=sin2x的图像向上平移1个单位后，得函数y=sin2x+1的图像，后纵坐标伸长到原来的3倍（横坐标不变），错误得函数表达式为y=3sin2x+1，这样纵坐标就没有伸长到原来的3倍。

长到原来的3倍（横坐标不变）后得到的为函数y=3[sin2(x+)+1]=3sin(2x +)+3的图像。

例题3、（2009年山东卷改编题2）：要将函数y=sin2x的图像变为函数y=3sin2x +1的图像，要做如何变换_________________。

【正确解答1】将函数y=sin2x的图像纵坐标伸长为原来的3倍（横坐标不变）得到函数y=3sin2x的图像，再图像向上平移1个单位得到y=3sin2x +1的图像。

三角函数图像变换的形式灵活多样，不管是先有表达式后写变换过程，还是先有变换过程后求表达式，但只要我们重视概念的教学，向学生讲清了各个参数ϕ,ω,A、B对图像影响的本质，学生就可以自己透过现象看清事物的本质也就能减少类似的错误了。