恢复饱和过程与潮流不对称耦合作用下的悬沙输运
李谊纯
(广西科学院 广西北部湾海洋研究中心,广西 南宁 530007)
恢复饱和过程与潮流不对称耦合作用下的悬沙输运
李谊纯
(广西科学院 广西北部湾海洋研究中心,广西 南宁 530007)
通过理想模型的解析解对河口悬移质泥沙输沙中恢复饱和过程与潮流不对称耦合作用下的长期净输运机制进行了研究,并给出了二者耦合作用下的悬沙长期净输运的定量表达及悬沙净输运方向与分潮相对位相的关系。研究认为,悬沙的长期净输运与泥沙的恢复饱和过程及潮流不对称存在密切关系。对于仅单频潮波作用的情况,恢复饱和过程不会导致悬沙净输运的产生;分潮与余流的相互作用将产生与余流方向一致的净输运;悬沙的净输运方向与潮流不对称的方向并不完全一致;对于频率满足一定条件的分潮的组合,不论该分潮组合是否导致潮流不对称,均会产生悬沙的净输运;净输运量是分潮组合中各分潮流速的振幅、相对位相及相对恢复饱和时间的函数。对于某一分潮组合,悬沙净输运与潮流不对称方向改变时,二者的相对位相阈值之间的偏差随恢复饱和时间的增大而增大。
悬沙;潮流不对称;恢复饱和时间;倍潮;耦合作用;潮波变形
潮波进入近岸及河口,由于水深、地形等条件的改变而发生变形是物质输运的重要动力机制。潮波变形可通过潮汐不对称和潮流不对称来定量研究。关于潮汐不对称与潮流不对称之间的关系并无明确的研究定论,对于物质输运而言,潮流不对称更具指示性。潮流不对称现象是潮汐运动的基本特征之一,早期的研究多集中于半日潮海区,利用M2分潮及其倍潮波M4、M6分潮之间振幅与相位的相对关系研究潮波在近岸变形的程度与方向[1-2]。而在全日潮海区,潮汐运动中起主要作用的是K1、O1等分潮,而M2、M4等分潮的作用则处次要位置,所以在半日潮海区的研究方法不能应用于全日潮海区。Nidzieko利用偏度对潮汐不对称进行了研究[3],Song等在此基础上进行了拓展[4]。关于潮流不对称以及其与泥沙输运之间的关系,不少学者进行了有益的探讨,如Van De Kreeke等利用潮流不对称进行了推移质输沙的研究[5];Sivakholundu等基于潮汐不对称进行了河道稳定性方面应用[6];Ranasinghe等研究了全日潮的海域的潮流不对称现象,并计算了推移质输沙量,进而对比研究了二者的相关性[7]。恢复饱和系数是反映悬移质不平衡输沙时,含沙量向饱和含沙量即挟沙能力靠近的恢复速度的重要参数。韩其为等根据由泥沙运动统计理论建立的扩散方程在底部的边界条件、导出了恢复饱和系数的定义及方程,并在某种假定下.给出有关参数及恢复饱和系数的表达式[8]。Chernetsky等利用垂向二维模型及底床变形模型研究了潮汐不对称与泥沙沉降滞后对河口悬沙输运的作用[9]。贺宝根等通过对长江口实测资料进行统计分析研究了泥沙饱和度随时间的变化[10]。Hoitink等对悬沙输运过程中恢复饱和时间(adaption time)与K1、O1、M2、M4分潮导致的潮流不对称进行了的研究[11]。这里在Hoitink工作的基础上,研究了包括余流及其它分潮在内的潮流不对称与恢复饱和过程耦合作用下的悬沙净输运的一般形式,探讨了潮流不对称和恢复饱和过程对悬沙净输运的影响机制。
1 恢复饱和过程与潮流不对称耦合作用下的悬沙输运
1.1理想模型及其解析解
平面二维悬沙输运方程可写为:
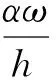
方程(2)的解可表示为:
式中:c0为积分常数,可视为泥沙初始浓度。李瑞杰等[12]认为,在水流挟沙力的计算中采用流速的平方关系式,物理意义清晰,能量关系明确,形式简单。在实际应用时,适当选取系数,水流挟沙力采用形式简单的平方关系式是完全可行的。因此,在本次研究中取水流挟沙力的形式为:
其中,k为系数。V为流速,可表示为:
其中,下标i取“0”代表余流;Vi为分潮流速;Ai,ωi,φi分别为分潮流速的振幅、频率和位相。
1.2悬沙净输运的导出
式(3)给出了理想模型中考虑悬沙恢复饱和时间的悬沙浓度的表达式。将式(4)、式(5)代入式(3)并整理可得:
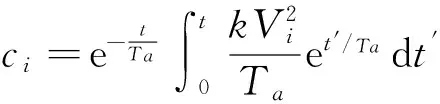
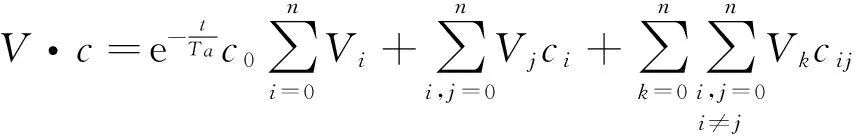
(7)
V·c为单位时间通过单位断面面积的输沙量,对其取长时间平均则可得长时间的悬沙净输沙率。分别对式(7)中右端三项取长时间平均,经计算可知,第一项的长时间平均为0,即泥沙的初始浓度对悬沙长期净输运没有影响。对于第二、三项,可以通过分别对其中的每一项分别进行长时间平均予以分析。对于第二项有:
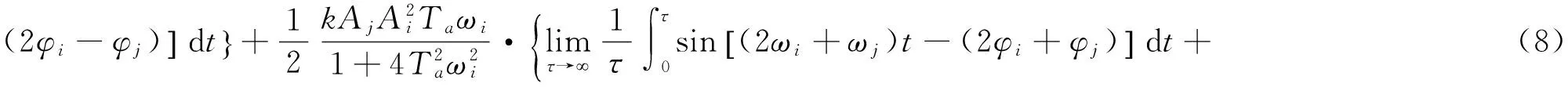
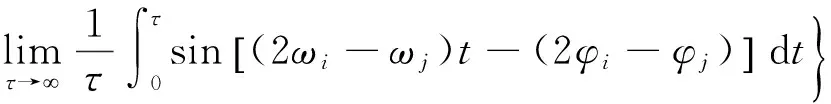
由式(8)可知,当不存在余流而只有单频率的潮波存在的情况下,Q等于0,即仅在单频波的作用下,尽管悬沙在输运过程中有恢复饱和过程的存在,但并不会导致净输运产生。同时显见,式(8)中的每一项在分潮频率满足一定的条件下可进一步简化为:


当ωi≠ωj≠0,2ωi-ωj=0时,
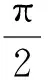
同理,对于式(7)中右侧方括号内的第三项有:
式(12)在一定条件下可简化为:
当ωi+ωj-ωk=0时,
当ωi-ωj+ωk=0时,
当ωi-ωj-ωk=0时,
可以看出,式(13)~式(15)组成了频率满足一定条件的3个分潮的组合情况下的悬沙净输运,如(K1O1M2)、(M2M4M6)的分潮流组合。而同时,其中也隐含了余流与分潮的相互作用以及两个分潮的组合作用下的悬沙净输运,如:当ωi=0且ωi=ωk时,Qijk为余流和分潮相互作用下的悬沙净输运的贡献;而对于ωi-ωj-ωk=0且ωj=ωk的情况,Qijk则代表了满足条件2ωi-ωj=0的两个分潮的组合对悬沙净输运的另一部分贡献,如(M2M4)、(M4M8)组合。
综合式(7)、式(9)~式(10)和式(12)~式(15),可以得到恢复饱和过程与潮流不对称耦合作用下的悬沙净输运的输沙率为:
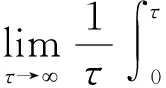
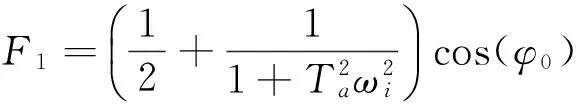
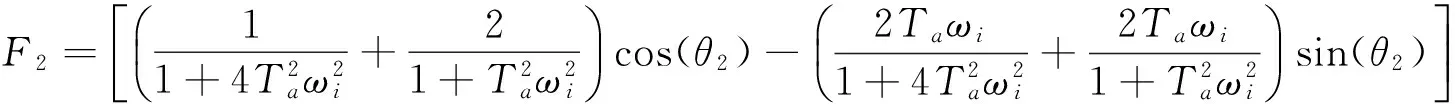
1.3F0、F1、F2和F3分析
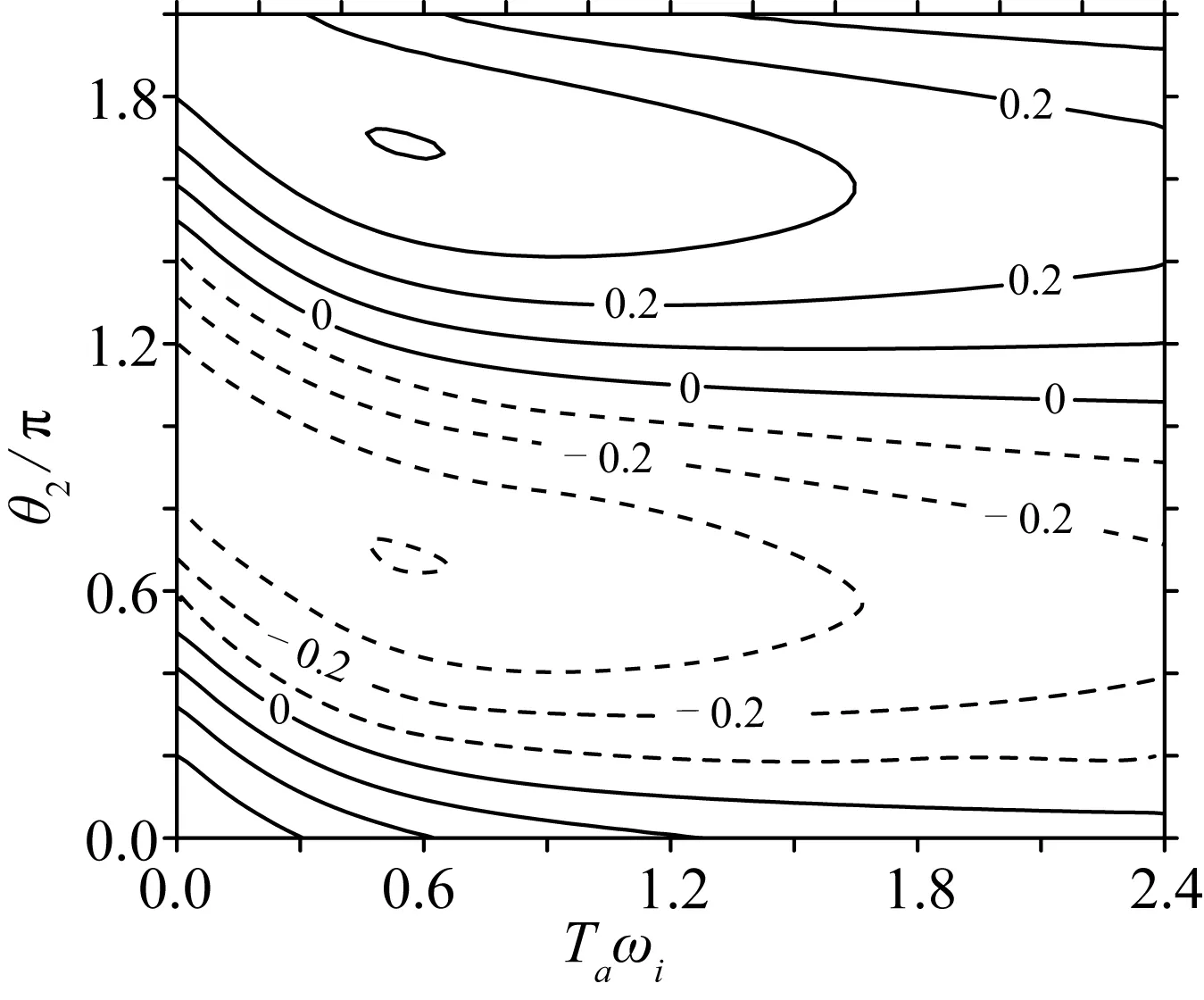
图1 F2随相对恢复饱和时间及相对位相的变化Fig. 1 Variation of F2 with the relative adaption time and relative phase
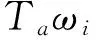
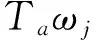
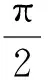
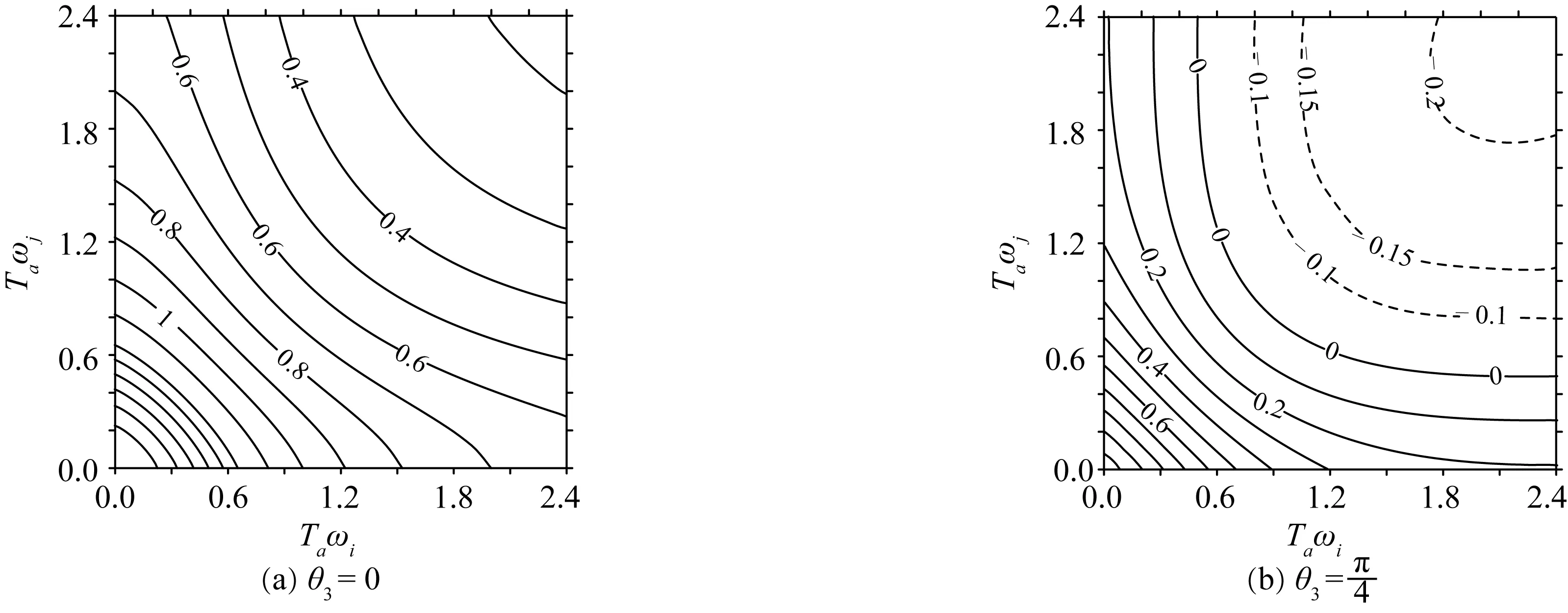
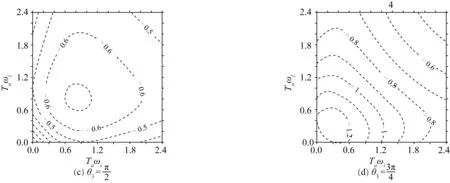
图3 不同相对位相下F3随相对恢复饱和时间的变化Fig. 3 Variation of F3 with the relative adaption time under different relative phases
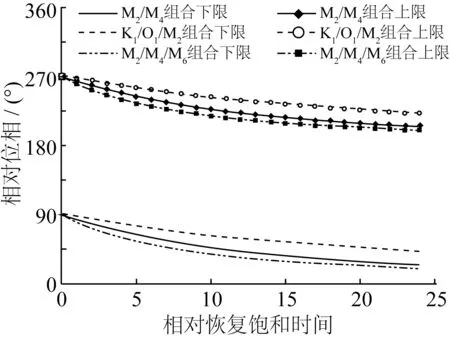
图4 相对位相对悬沙净输运方向的影响阈值随恢复饱和时间的变化Fig. 4 Variation of relative phase threshold of suspended sediment net transport directions with the relative adaption time
在实际海洋中,对潮流不对称影响最大的分潮主要是K1、O1、M2、M4及M6,对于潮汐和潮流不对称的研究也主要集中于K1、O1、M2、M4及M6分潮的相互作用[1-3,5-7]。因此,图4给出了M2M4、K1O1M2和M2M4M6的组合中相对位相对悬沙净输运的影响区间随Ta的变化。可以看出,对于一定的恢复饱和时间,悬沙净输运与潮流不对称的方向改变时,二者相对位相的阈值之间的偏差M2M4M6组合最大,M2M4组合次之,K1O1M2组合最小。对于某一分潮组合,该偏差随恢复饱和时间的增大而增大。
2 结 语
最后需要指出的是,天然河口及近岸水域由于受到地形、潮汐、径流、泥沙性质及气象等多种因素影响,实际情况极其复杂,而本模型及其解析解给出的是恢复饱和过程与潮流不对称二者耦合作用对悬沙输运的作用机理。因此前述结论在天然水域实际的悬沙输运判断中需视情况谨慎应用。
[1] MANOJ N T, UNNIKRSHANA A S, SUNDAR D. Tidal asymmetry in the Mandovi and Zuari Estuaries, the West Coast of India [J]. Journal of Coastal Research, 2009, 25(6):1187-1197.
[2] BLANTON J O, LIN G, ELSTON S A. Tidal current asymmetry in shallow estuaries and tidal creeks[J]. Continental Shelf Research, 2002, 22: 1731-1743.
[3] NIDZIEKO N J. Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides [J]. Journal of Geophysics Research, 2010, 115, C08006, doi: 10.1029/2009JC005864.
[4] SONG D H, WANG X H, KISS A E, et al. The contribution to tidal asymmetry by different combinations of tidal constituents [J]. Journal of Geophysics Research, 2011, 116, C12007, doi: 10.1029/2011JC007270.
[5] VAN DE KREEKE J, ROBACZEWSKA K. Tide-induced residual transport of coarse sediment: application to the EMS estuary [J]. Netherlands Journal of Sea Research, 1993, 31(3):209-220.
[6] SIVAKHOLUNDU K M, MANI J S, IDICHANDY V G, et al. Estuarine channel stability assessment through tidal asymmetry parameters [J]. Journal of Coastal Research, 2009, 25 (2):315-323.
[7] RANASINGHE R, PATTIARATCHI C. Tidal inlet velocity asymmetry in diurnal regimes[J]. Continental Shelf Research, 2000, 20:2347-2366.
[8] 韩其为,何明民. 恢复饱和系数初步研究[J]. 泥沙研究. 1997(3):32-40. (HAN Qiwei, HE Mingmin. A study on coefficient of saturation recovery[J]. Journal of Sediment Research, 1997(3):32-40. (in Chinese))
[9] CHERNETSKY A S, SCHUTTELAARS H M, TALKE S A. The effect of tidal asymmetry and temporal settling lag on sediment trapping in tidal estuaries [J]. Ocean Dynamics, 2010, 60:1219-1241.
[10] 贺宝根,王初,周乃晟, 等. 长江口潮滩浅水区域流速与含沙量的关系初析[J]. 泥沙研究, 2004(5):56-61.(HE Baogen, WANG chu, ZHOU Naisheng, et al. Study on relationship between sediment and velocity in the shallow water area of intertidal flats in the Yangtze Estuary[J]. Journal of Sediment Research, 2004(5):56-61. (in Chinese))
[11] HOITINK A J F, HOEKSTRA P, WAN MAREN D S. Flow asymmetry associated with astronomical tides: Implications for the residual transport of sediment [J]. Journal of Geophysics Research, 2003, 108, C103315, doi:10.1029/2002JC001539.
[12] 李瑞杰,罗锋,周华民. 水流挟沙力分析与探讨[J]. 海洋湖沼通报, 2009(1):88-94. (LI Ruijie,LUO Feng,ZHOU Huamin. Study on the flow induced sediment carrying capacity[J]. Transactions of Oceanology and Limnology, 2009(1):88-94. (in Chinese))
On the net suspended sediment transport under coupling effects of adaptation time and tidal current asymmetry
LI Yichun
(Guangxi Beibu Gulf Marine Research Center, Guangxi Academy of Sciences, Nanning 530007, China)
Analytical solution of an ideal model was adapted to investigate the net suspended sediment transport under combined effects of adaptation time and tidal current asymmetry. The quantificational expression of long-term net transport of suspended sediment and the relationship between the direction of net sediment transport and that of the tidal current asymmetry were also deduced. The study shows that the long-term net transport is connected closely with the adaptation time and tidal current asymmetry. No net transport arises under a condition that only a single tide constituent exists. The combined effects of residual current and tidal constituents can cause a net transport with the same direction as that of the residual current. The direction of net transport is not always identical to the tidal current asymmetry. Net transport will be caused by some combinations of different tidal constituents that satisfied with certain conditions can account for net transport no matter the tidal current is asymmetric or not. The net transport is a function of amplitude, relative phase and relative adaption time. To a certain combination of tidal constituents, the deviation of relative phases which indicate the directions of net suspended sediment transport and tidal current asymmetry will be larger with the adaption time increasing.
suspended sediment; tidal current asymmetry; adaption time; overtides; coupling effect; tidal wave deformation
TV148
A
10.16483/j.issn.1005-9865.2015.01.008
1005-9865(2015)01-0066-07
2014-02-17
广西自然科学基金北部湾重大专项(2011GXNSFE018002)
李谊纯(1977-),男,河北人,工程师,博士,主要从事河口海岸学研究。E-mail:ychli@vip.sina.com

