高校相关系数授课的新思路
周齐 黄少骞(华北理工大学理学院河北唐山063000)
高校相关系数授课的新思路
周齐 黄少骞
(华北理工大学理学院河北唐山063000)
针对目前高校统计专业方向关于相关系数以及相关性存在的一些问题,指出了目前大部分教材对于相关系数及相关性的介绍都存在相对混乱、界定不清的问题,本文由相关关系的定义,通过相关系数的内涵,结合一定的定理与性质,给出了相关系数与相关性程度对应的一套完整定义及评价体系,对厘清相关程度等概念具有较好的作用,同时也有利于高校教师的讲解以及学生形成较为全面、合乎逻辑的知识体系。
相关系数相关性相关程度简单相关系数
目前高校教材关于相关关系、相关系数、样本相关系数都存在界定不清,表述相对混乱的情况,对教学效果,尤其是对学生的理解不能形成系统清晰的理解脉络,本文就此问题,提出相关系数的一些讲授思路:
首先,关于关系大致存在函数关系和相关系两种,如下表:

表一:两种关系
那么,接下来关于相关关系,从广义上按类型可以分为如下:

这是从关系“形态“上进行的分类,稍后会指明,概率论中的相关系数等都是作为线性相关的量度,即本科阶段关于相关关系的研究对象主要是线性相关。
从程度上划分,可以分为完全相关、不完全相关和不相关:

完全相关 当一个变量的数量完全由另一个变量的数量变化所确定时,二者之间即为完全相关。完全相关即为函数关系。不完全相关 如果两个变量的关系介于完全相关和不相关之间,称为不完全相关。不相关 又称零相关,当变量之间彼此互不影响,其数量变化各自独立时,则变量之间为不相关。在这里,相当于概率论当中的“独立”。
可以认为,这里对于完全相关、不完全相关和不相关的表述给出的是完全相关、不完全相关和不相关的定义。
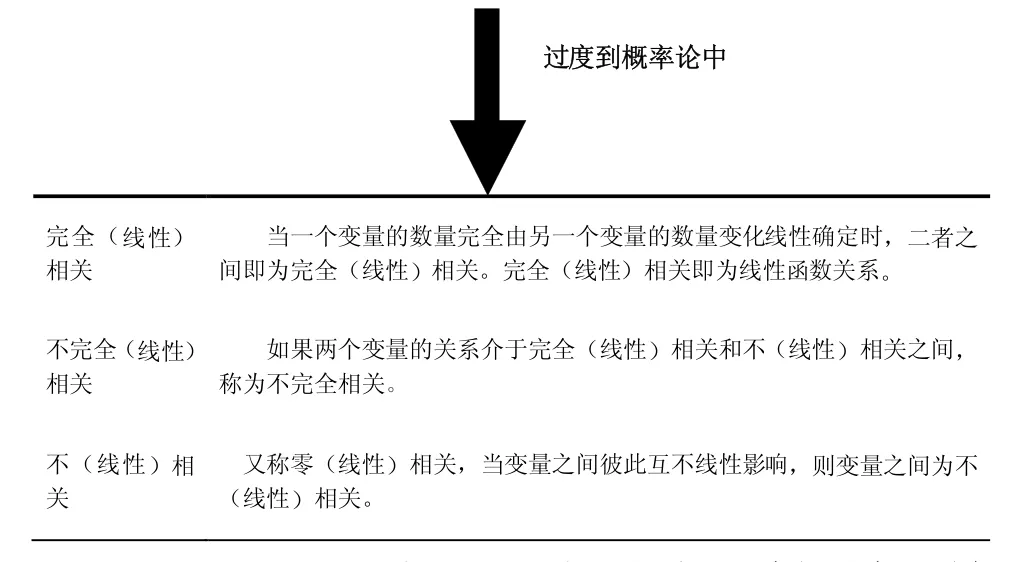
过度到概率论中完全(线性)相关当一个变量的数量完全由另一个变量的数量变化线性确定时,二者之间即为完全(线性)相关。完全(线性)相关即为线性函数关系。不完全(线性)相关如果两个变量的关系介于完全(线性)相关和不(线性)相关之间,称为不完全相关。不(线性)相关又称零(线性)相关,当变量之间彼此互不线性影响,则变量之间为不(线性)相关。
现在的问题是对于所给定的两个总体,很难通过定性的定义进行判定,所以定义相关系数进行量化:
首先根据相关系数定义和柯西—施瓦茨不等式可以得到如下定理:
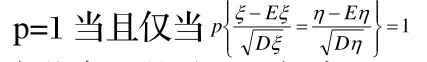
由此定理基础,“以概率一”和“充要性”,有理由做出如下定义,进行一次近似,完成完全线性相关的量化判定标准:
若随机变量ξ和η的相关系数p=1,则ξ和η完全线性相关/具有完全线性关系。
另外,根据相关系数本身的内涵,还会定义:
若随机变量ξ和η的相关系数p=0,则称ξ和η不线性相关。
注意:p=0并不意味着和不相关,只是不线性相关,有可能具有其他相关关系。
若随机变量ξ和η的相关系数绝对值[0.8,1],则称ξ和η高度线性相关。
若随机变量ξ和η的相关系数绝对值[0.5,0.8],则称ξ和η中度线性相关。
若随机变量ξ和η的相关系数绝对值[0.3,0.5],则称ξ和η低度线性相关。
若随机变量ξ和η的相关系数绝对值[0,0.3],则称ξ和η线性相关程度极弱。
但是由于两个总体之间的相关系数仍旧是不好求得的,所以保留量化的优势,进一步定义简单相关系数,可以发现简单相关系数具有性质:
样本相关系数等于一⇔样本点在一条直线上
由此性质基础,结合样本相关系数是总体相关系数的极大似然估计,进行二次近似,可以定义:
若随机变量ξ和η的样本相关系数r=1,则ξ和η完全线性相关/具有完全线性关系。
同理可以有如下定义(在这里之所以写成具有充要双向的定义形式,为的是于总体相关系数的相关定义形成统一“整体齐性”)
若随机变量ξ和η的样本相关系数绝对值大于%5,则ξ和η高度显著线性相关
若随机变量ξ和η的样本相关系数绝对值[1%,5%],则ξ和η显著线性相关
若随机变量ξ和η的样本相关系数绝对值小于1%,则ξ和η线性相关程度不明显。
关于边界等号的位置,在这里不在作为讨论的重点。
若随机变量ξ和η的样本相关系数为零,则ξ和η不线性相关
在这里,主要是通过相关系数的内涵,根据定理性质采取人为定义的方式对相关性程度与相关系数值做出了对应,国内大部分教材都是沿续这一思路,国外的一些教材是从线性回归模型的角度给出了另外形式的相关系数的定义式,根据相关系数具体取值对回归方程的性态影响角度对应相关性程度,可能在某种意义上规避了本文需要“近似”的弱点,更能贴近相关关系的定义,但国外思想涉及到回归方程建立的思路角度,与我曾经发过一篇论文《回归分析与灰色预测的比较与联合应用》不是一致的,所以放弃了国外思想。
[1]陈希孺,何声武.不独立和不相关[J].应用概率统计,1996,02:193-195.
[2]蔡军.关于不相关和不独立问题的几点注记[J].扬州师院学报(自然科学版),1999,03:45-50.
[3]章舜仲,王树梅.相关系数矩阵与多元线性相关分析[J].大学数学,2011,01:195-199.
[4]杨闻起.强线性相关与弱线性无关[J].宝鸡文理学院学报(自然科学版),2009,02:1-3.
[5]李秀敏,江卫华.相关系数与相关性度量[J].数学的实践与认识,2006,12:199-192.

