参考价格符合峰终定律的多产品动态定价模型
毕文杰,孙颖慧,田柳青
(中南大学商学院,湖南长沙410083)
参考价格符合峰终定律的多产品动态定价模型
毕文杰,孙颖慧,田柳青
(中南大学商学院,湖南长沙410083)
针对客户存在参照效应,且参考价格更新符合峰终定律的情况,建立了多产品动态定价模型.通过构建价值函数的合理上界,解决了动态规划模型非光滑的问题,给出了动态定价模型稳态价格的解析解,并利用效用函数的超模性证明了最优价格随时间单调递增.通过数值计算,将该模型分别与只考虑单个产品价格的定价模型和短视定价模型进行了比较.结果表明,非核心产品的价格要高于核心产品的价格,且考虑参照效应的长期定价策略的各期价格高于相应短期定价策略的价格.
峰终定律;参照依赖;损失厌恶;动态定价
1 引 言
对于大多数企业来说,最关心的问题是如何提高企业的利润.研究表明,尽管通过提高库存和物流管理水平可以很好地降低供应链成本,但通过制定科学而灵活的动态价格策略,是企业提高利润的最快和最有效的方法:定价提高1%,企业的运营效益往往就能提高7%–15%[1].鉴于动态定价的重要性,学者们对其进行了大量的研究,提出了不同的理论体系和模型.早期的经典动态定价模型如Gallego和Van Ryzin[2]提出的GVR模型,大都假设客户是短视的,不考虑厂商后期的价格策略对客户购买行为的影响.随着动态定价模式的普及和信息技术的发展,越来越多的客户的购买行为体现出策略性.所以,考虑客户策略行为的动态定价问题迅速成为学者们研究的热点,并产生了丰富的研究成果.例如毕功兵等[3]针对消费者策略行为,在单个厂商销售两种可替代产品情况下,建立了两周期动态定价模型.但考虑客户策略行为的动态定价研究又走向了另一个极端,绝大多文献将客户假设为完全理性的.然而,来自心理学实验和行为博弈领域的大量研究表明[4]决策者会系统地偏离完全理性假设,表现出如偏好不一致,记忆力,推理能力有限,随机最优反应,参照依赖等一系列有限理性的行为.而这些行为对市场需求和企业利润都将产生重要影响.考虑客户有限理性行为的动态定价问题也成了学术界新的研究热点,也已有学者对此作出研究[5].
最近的实证表明客户在购买商品时存在参考效应[6].大量文献研究了参考价格的锚定机制,详见苏凇和黄劲松[7]的综述.其中,Rajendran和Tellis[8]对过去购买价格进行几何平均得到参照价格.Mazumdar和Papatla[9]将所有历史价格进行指数平滑得到参照价格.Armstrong和Chen[10]对市场垄断价格进行平均得到参照价格.Biresch等[11]比较了当时流行的几种参照价格模型,认为“指数平滑模型”与实验数据的匹配度最高.随着研究的深入,学者们也越来越多的在动态定价中引入参考价格.Sorger[12]研究了参考效应下动态定价和广告策略的结合.Popescu和Wu[13]在假设参照价格服从指数平滑的基础上,构建了动态定价模型,并证明了最优价格路径的单调性与收敛性.Huh等[14]将此模型扩展到两阶段多周期的定价问题中,得到类似结果.程岩[15]还根据客户的参考价格对客户进行细分,并基于此研究了季节性,时尚类产品的动态定价问题.然而,一些关于参照价格的研究对指数平滑模型产生了质疑.Dickson等[16]发现消费者对价格的记忆是有限的,只有47.1%的人能够在购买后能说出其购买产品的价格.Fredrickon和Kahneman[17]提出了“峰终定律”,认为人们对体验的记忆由两个因素“峰值”和“终值”决定,所谓“峰值”是指最大值(最小值),“终值”是指最近的值.在定价问题中,“价格峰值”指过去的最高(最低)价格,“价格终值”指最近一期的价格. Nasiry和Popescu[18]在Fredrickon和Kahneman研究的基础上提出了消费者基于峰终定律锚定参考价格的单产品动态定价模型,他们注意到如果更多的顾客锚定在最低价格上,那么相应的价格范围也就越宽,扩展了前面研究的结论.
关于多产品的参考价格形成机制,本文借鉴了Calicchio和Krell[19]对拉丁美洲零售商价格策略的调查研究.Calicchio和Krell发现,少数商品的价格(又称为核心商品)决定了客户对该零售商店的整个价格预期.因此,核心商品的定价对零售商利润非常重要.例如,零售商可以通过给核心商品制定较低的价格来吸引客户访问他们的商店,而通过非核心商品的销售获取额外的收益.本文正是基于这种现象,假设客户的参考价格有两种机制,一种是Product-level,即参考价格只受该产品本身价格的影响;另一种是Store-level,参考价格受多个核心产品的价格共同影响.而本文重点分析参考价格符合第二种机制下的动态定价问题.
本文在假设参考价格受多个核心产品的价格共同影响,且参考价格的更新符合峰终定律的基础上,构建了多产品动态定价模型,并对其进行分析求解.
2 多产品动态定价模型
2.1 模型假设与主要符号说明
首先考虑一个垄断厂商销售多种产品的利润最大化问题.在该市场中,消费者的购买决策受当期的价格及过去的价格的影响,即参照效应影响需求.
假设1 假设各个产品的需求相互独立,消费者在价格方面的参照效用影响产品的需求,且参照效用为线性的.产品需求函数为
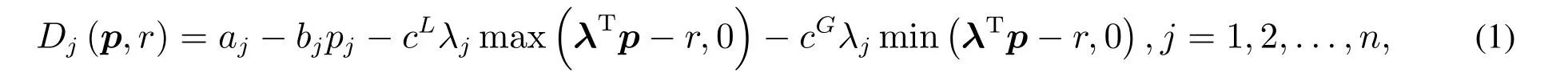
其中p=(p1,p2,...,pn)T为多个产品的价格向量,r为参考价格,aj>0,bj>0,基础需求函数dj(pj)= aj−bjpj是价格的线性减函数.λ为非负向量,表示各产品在消费者心中的权重,有1Tλ=1,λTp是该厂商产品价格的加权平均,代表了当前该厂商的综合价格水平.式(1)中,cL表示消费者对损失的敏感程度,cG表示消费者对赢得的敏感程度,0cL1,0cG1.如果cG=cL,消费者为损失中性的,则需求函数是光滑的(连续可微).如果cG
此外,假设消费者的参照价格是store-level的,即消费者对整个厂商的价格有总体上的感受,称为厂商综合价格水平,即λTp,其得失为综合价格水平与参考价格比较而来.由于不同的产品在消费者心中的权重不同,故某个产品需求的参照效应为综合价格水平产生的参照效应乘以其权重.从式(1)可知,当参考价格rλTp时,Dj(p,r)=aj−bjpj−cGλj(λTp−r);当参考价格r< λTp时, Dj(p,r)=aj−bjpj−cLλj(λTp−r).
假设2 消费者的参照价格受所有商品过去价格的影响,其形成和更新机制服从峰终定律,即为过去价格的最小值或最大值(本文考虑的是最小值)与上期价格的加权值,即

其中mt−1=min(mt−2,λTpt−1)为过去综合价格水平的最小值,0α<1为消费者的记忆因子,代表最小价格对消费者影响的比重.
2.2 多产品动态定价模型
在前面的假设下,厂商的动态定价问题就是使得产品所有时期销售收入总价值最大化,即
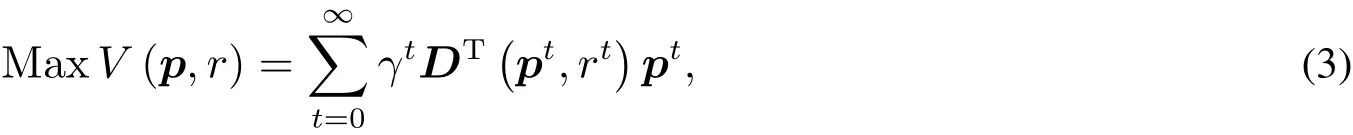
其中γ为折扣因子,D(pt,rt)为销售量向量.
参照价格的演化方程为

此问题的贝尔曼方程为
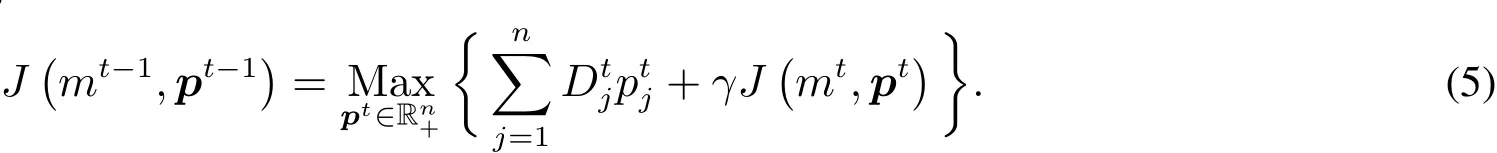
式(5)的约束条件为式(4).
因价值函数J(mt−1,pt−1)非光滑,将按以下步骤求解稳态价格.首先,找到价值函数J(mt−1,pt−1)的一个光滑上界,即

然后,根据引理1和引理2得出模型(5)的稳态价格.
引理1 J(mt−1,pt−1)(pt−1),∀mλTp.(证明见附录)
引理2 模型(6)的稳态价格同时为模型(5)的稳态价格.(证明见附录)
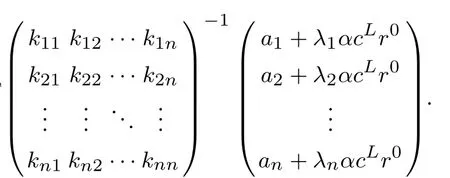
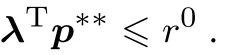
定理1 模型(5)多产品动态定价存在一个稳态价格p∗∗,满足下式
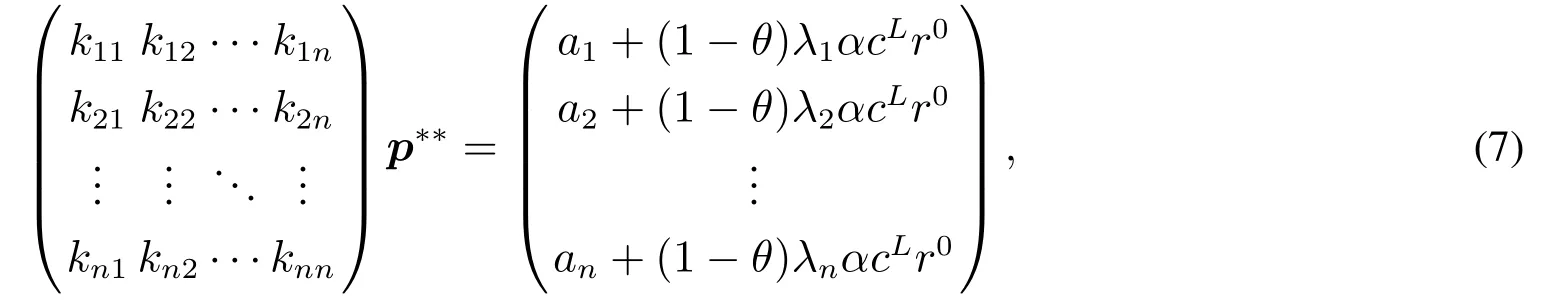
其中kii=2bi+(1−θ)λiλicL[2−(1−α)(1+γ)]+θcGλiλi(1−γ),kij=(1−θ)λiλjcL[2−(1−α)(1+ γ)]+θcGλiλj(1−γ),.
具体可分如下几种情况:
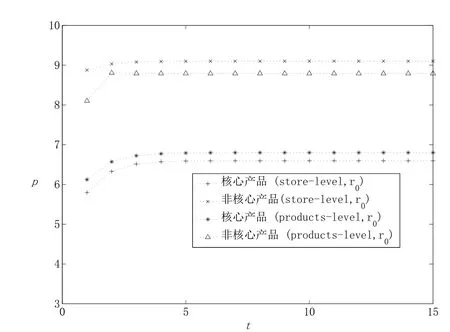
1)当r0 kii=2bi+λiλicL[2−(1−α)(1+γ)],kij=λiλjcL[2−(1−α)(1+γ)],. 2)当r0∈[q,s]时,∃θ(r0)∈[0,1],使得λTp(θ(r0),r0)=r0,稳态价格p∗∗=p(θ(r0),r0)即为θ= θ(r0)时式(7)的解,其中 kii=2bi+(1−θ(r0))λiλicL[2−(1−α)(1+γ)]+θ(r0)cGλiλi(1−γ),kij=(1−θ(r0))λiλjcL[2−(1−α)(1+γ)]+θ(r0)cGλiλj(1−γ),. 3)当r0>s时,稳态价格p∗∗=p(1,sn),即为θ=1时式(7)的解,其中 kii=2bi+cGλiλi(1−γ),kij=cGλiλj(1−γ),. q和s分别为θ=0和θ=1时r=λTp∗∗的解.(证明见附录) 定理2 最优价格随时间单调递增,且如果r0s,则λTpr0.如果r0>s,则mt−1>s,其中q和s的含义同定理1.(证明见附录) 定理2说明,如果r0s,消费者对产品价格整体的印象(两个产品价格的线性组合)总是大于其最初的参照价格.即最小的价格并不随时间变动,各周期的参照价格也都在原来的区域中.而当r0>s时,最小的价格就会随时间的变动而变动,但不会小于s,各周期的参照价格也都在原来的区域中. 定理3 模型(7)中参数aj,bj,cL,cG及λj与稳态价格pj的影响为: 1)稳态价格pj随aj增加而递增,随bj增加而递减,且核心产品的稳态价格pj随aj,bj变化的幅度比非核心产品的小. 2)稳态价格pj随cL,cG的增加而递减. 3)核心产品稳态价格pj随λj的减少而递增,非核心产品稳态随λj的减少而递减. (证明见附录) 为了更直观的了解核心产品与非核心产品的稳态价格与各参数之间的关系.本节将针对两产品的情况,在给定参数的情况下,比较Store-level定价策略与Product-level定价策略的最优价格路径.Product-level定价策略模型假设消费者的参照价格仅仅受其购买产品过去价格的影响,其动态定价问题如下 假设消费者的初始参照价格相等,两种产品需求函数中各系数也相同,且各参数取值为r0=4, a1=a2=100,b1=b2=5,cL=20,cG=10,α=0.2,γ=0.95,λ1=0.8,λ2=0.2.图1展示了两种定价策略下的最优定价路径. 从图1可以看出,两种策略下,非核心产品的价格都高于核心产品.因为两种策略下消费者对核心产品参照依赖程度大于非核心产品.然而,与Product-level比较,在Store-level下,非核心产品的价格更高,核心产品的价格更低.说明Store-level策略通过较低的核心产品价格降低消费者Store-level的参照价格,以吸引更多的消费者购买产品.而非核心产品的提高对消费者参照价格和需求影响较小,可以获得较高的利润来弥补因核心产品价格降低造成的损失. 当厂商在做决策时不考虑价格对利润的长期影响时,称之为短视厂商,其定价模型为式(5)中γ=0的情况.可参照定理1求得该模型的稳态,图2比较了短视型厂商的价格策略和最优定价策略. 图1 Store-level和Product-level策略下的最优价格路径Fig.1 Optimal price path for strategy of Store-level and Product-level 图2 短视型厂商的价格策略与最优定价策略比较Fig.2 Optimal price path for optimal strategy versus myopic strategy 从图2可以看出两种定价策略下,非核心产品的价格都高于核心产品.最优策略的价格高于短视型厂商的价格策略.这个结果与Nasiry和Popescu[18]单产品定价的研究相同. 本文构建了参照价格符合峰终定律的多产品动态定价模型,得出了稳态价格的解析解,证明了最优价格随时间单调递增,并通过稳态价格的解析解分析了各参数变化对稳态价格的影响.通过数值算例具体描述了最优价格路径,结果表明厂商可以通过减小核心产品的价格来降低消费者的参照价格,从而吸引更多的顾客.本文还通过数值分析将本文所建模型和短视型厂商定价模型分别进行了比较,结果说明长期定价策略的各期价格高于短视的定价策略. 本文未考虑消费者的策略行为.而面对动态定价的商品时,消费者更可能会表现出一些策略行为,例如等待合适的价格购买.因此,将本模型应用到针对策略型消费者或是混合型消费者的定价中是个值得进一步研究的问题. [1]¨Ozer¨O,Phillips R.The Oxford Handbook of Pricing Management[M].Oxford:Oxford University Press,2012. [2]Gallego G,Van Ryzin G.Optimal dynamic pricing of inventories with stochastic demand over fnite horizons[J].Management Science,1994,40(8):999–1020. [3]毕功兵,王怡璇,丁晶晶.存在替代品情况下考虑消费者策略行为的动态定价[J].系统工程学报,2013,28(1):47–54. Bi Gongbing,Wang Yixuan,Ding Jingjing.Dynamic pricing based on substitutes and strategic consumers[J].Journal of Systems Engineering,2013,28(1):47–54.(in Chinese) [4]Cai W,Chen Y J.Intertemporal pricing with boundedly rational consumers[J].Journal of Revenue&Pricing Management,2011, 11(4):421–452. [5]Camerer C,Hua Ho T.Experience-weighted attraction learning in normal form games[J].Econometrica,2003,67(4):827–874. [6]Kalyanaram G,Winer R S.Empirical generalizations from reference price and asymmetric price response research[J].Marketing Science,1995,14(3):161–169. [7]苏 凇,黄劲松.参照价格理论研究新进展[J].经济学动态,2013(3):148–157. SuSong,HuangJinsong.Newresearchprogressofreferencepricetheory[J].EconomicPerspectives,2013(3):148–157.(inChinese) [8]Rajendran K N,Tellis G.Contextual and temporal components of reference price[J].Journal of Marketing,1994,58(1):22–34. [9]Mazumdar T,Papatla P.Loyalty differences in the use of internal and external reference prices[J].Marketing Letters,1995,6(2): 111–122. [10]Armstrong M,Chen Y.Discount pricing[R].Economics Series Working Paper 605,Department of Economics,University of Oxford, 2012. [11]Briesch R A,Krishnamurthi L,Mazumdar T,et al.A comparative analysis of referenceprice models[J].Journal of Consumer Research,1997,24(2):202–214. [12]Sorger G.Reference price formation and optimal marketing strategies[J].Optimal Control Theory and Economic Analysis,1988, 3(3):97–120. [13]Popescu I,Wu Y.Dynamic pricing strategies with reference effects[J].Operations Research,2007,55(3):413–429. [14]Huh W T,Kachani S,Sadighian A.A two-stage multi-period negotiation model with reference price effect[J].Journal of Revenue& Pricing Management,2010,9(5):443–475. [15]程 岩.电子商务中面向产品线的动态定价方法研究[J].系统工程学报,2010,25(4):533–539. Cheng Yan.Research on method of dynamic pricing for product line in E-commerce[J].Journal of Systems Engineering,2010, 25(4):533–539.(in Chinese) [16]Dickson P R,Sawyer A G.The price knowledge and search of supermarket shoppers[J].The Journal of Marketing,1990,54(3): 42–53. [17]Fredrickson B L,Kahneman D.Duration neglect in retrospective evaluations of affective episodes[J].Journal of Personality and Social Psychology,1993,65(1):45–55. [18]Nasiry J,Popescu I.Dynamic pricing with loss-averse consumers and peak-end anchoring[J].Operations Research,2011,59(6): 1361–1368. [19]Calicchio N,Krell A.Price promotions in Latin American retailing[J].McKinsey Quarterly,2007,43(4):57–59. [20]Smith J E,McCardle K F.Structural properties of stochastic dynamic programs[J].Operations Research,2002,50(5):796–809. [21]Topkis D M.Supermodularity and Complementarity[M].Princeton:Princeton University Press,1998. 附录 引理与定理证明 定理1及引理2证明 首先求解模型(6)的稳态解,即式(6)对求偏导,并使又稳态时故得 求解得 其中kii=2bi+(1−θ)λiλicL[2−(1−α)(1+γ)]+θcGλiλi(1−γ),kij=(1−θ)λiλjcL[2−(1−α)(1+γ)]+θcGλiλj(1−γ), 令r=λTp∗∗(假设3),结合式(9)得 由于式(10)是关于θ的单调减函数,当r∈[q,s]时,存在θ∈[0,1]使得式(10)成立,即r=λTp.则求解得到模型(6)的稳态解即为定理1中的三种情况. 引理2的证明,证明模型(6)的稳态解也是模型(5)的稳态解. 与式(6)相同,即这个策略在模型(5)和模型(6)中有同样的价值函数,所以p∗∗=p(0,r0)也是式(5)的稳态. 3)当mt−1∈(s,],p∗∗=p1,r0时, 定理2证明 1)根据Smith的定理5[20]可知J(m,p)在(−m,p)具有子模性,因此可得出最优价格随时间单调递增.当r0s时,有λTpr0,由单调性可知pt单调递增,所以r0=m0=min(λTp0,λTp1,...,λTp∞). 定理3证明 假设厂商生产两种产品,其中产品1为核心产品,产品2为非核心产品,厂商的稳态价格为 其中k11=2b1+(1−θ)cL[2−(1−α)(1+γ)]λ12+θcG(1−γ)λ12,k12=k21=(1−θ)cL[2−(1−α)(1+γ)]λ1λ2+ θcG(1−γ)λ1λ2,k22=2b2+(1−θ)cL[2−(1−α)(1+γ)]λ22+θcG(1−γ)λ22. 所以稳态价格是随cG递增而递减的. 由分子 Multi-product dynamic pricing model with reference price submitting to peak-end rule Bi Wenjie,Sun Yinghui,Tian Liuqing This paper develops a multi-product dynamic pricing model based on consumers’reference effect and the updating scheme of reference price which meets the peak-end rule.A reasonable upper bound of the value function is built to solve the non-smooth problem of the dynamic programming model.The analytical solution of steady state price is obtained by solving this problem.That the optimal price increases monotonically with time is proved by the super-modularity of the utility function.A numerical example is given to compare this model with the model which only considers one product’s price and the myopic pricing model respectively.The results show that the price of non-core products is higher than that of core products and the price of long-term pricing strategy is higher than that of myopic strategy for each period. peak-end rule;reference dependence;loss-averse;dynamic pricing F272.3 A 1000−5781(2015)04−0476−09 10.13383/j.cnki.jse.2015.04.005 2013−12−13; 2014−07−14. 国家自然科学基金资助项目(71371191;71210003;71221061);湖南省社会科学基金资助项目(12YBB272). 毕文杰(1972—),男,湖南常德人,博士,教授,研究方向:行为运筹研究,E-mail:beenjoy@126.com; 孙颖慧(1989—),女,山东济宁人,硕士,研究方向:动态定价,E-mail:syhjnr830@163.com; 田柳青(1989—),女,湖北钟祥人,硕士,研究方向:动态定价,E-mail:775926546@qq.com.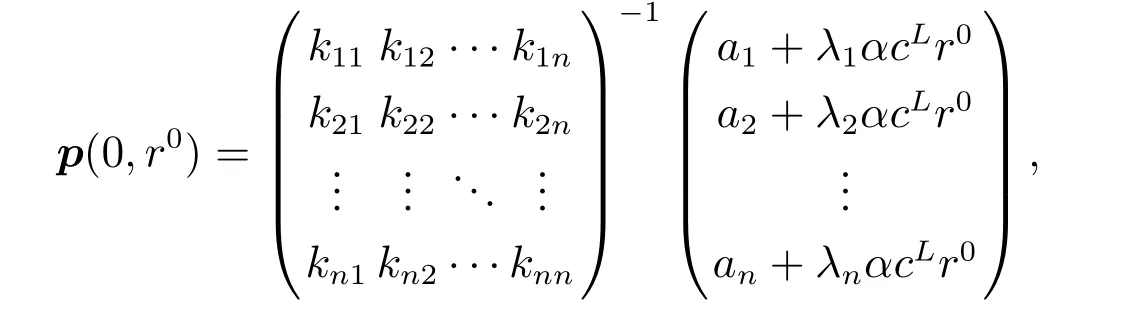


3 数值算例


4 结束语
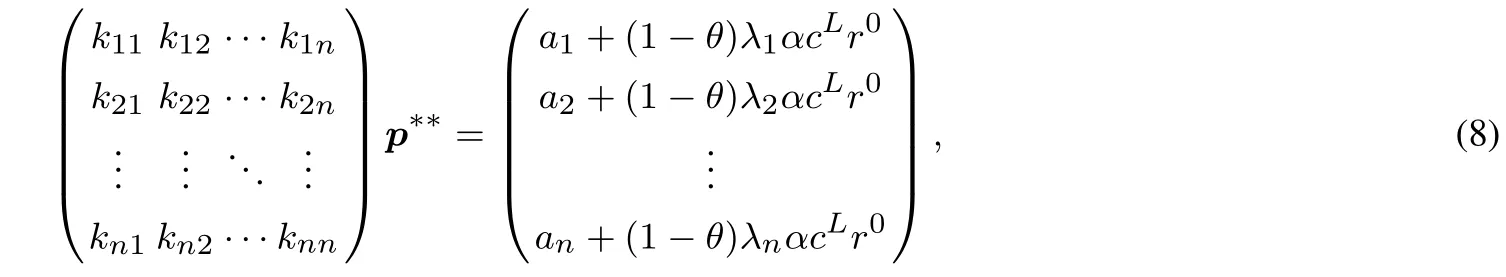
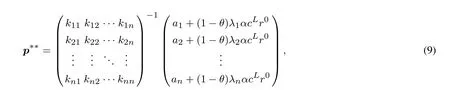




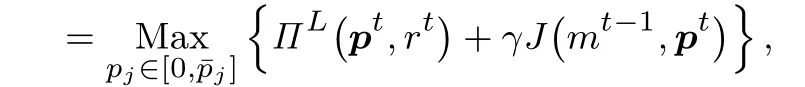
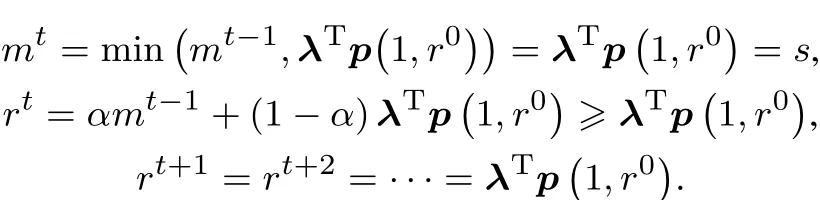
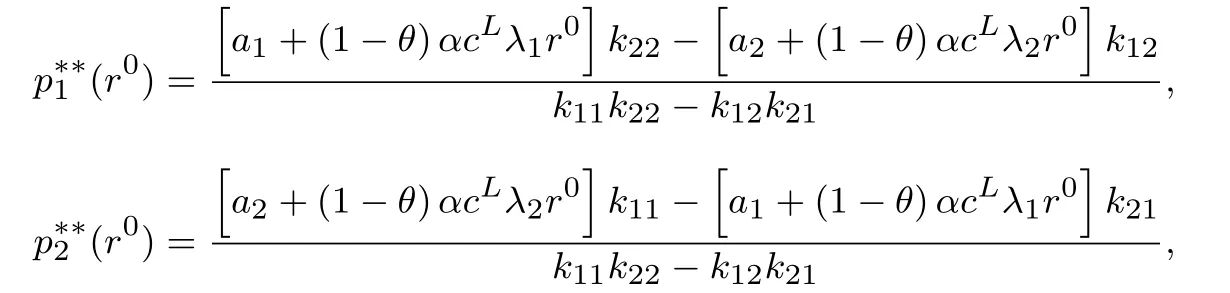
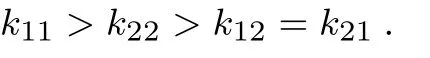
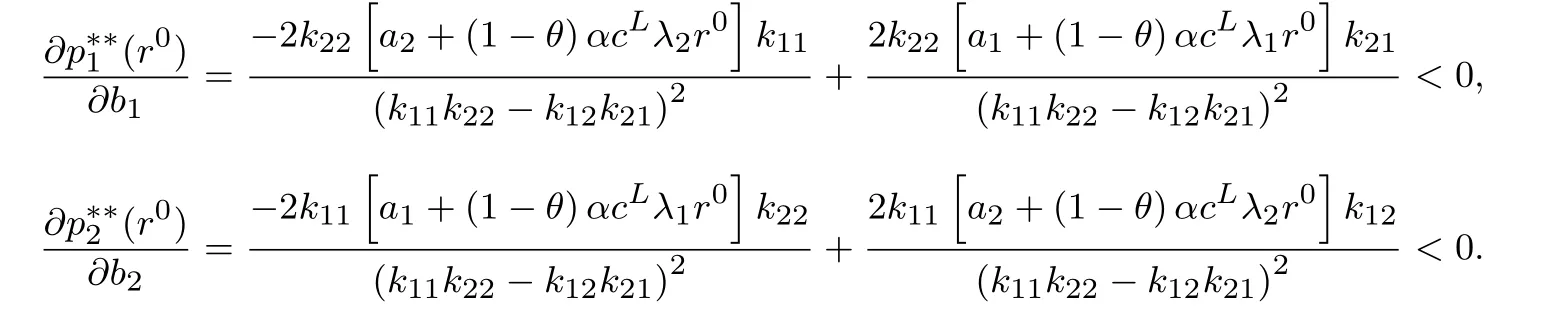
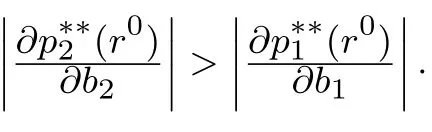


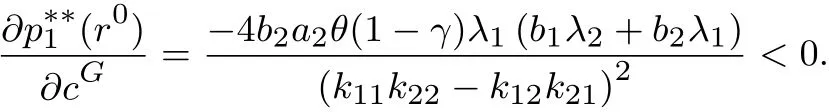
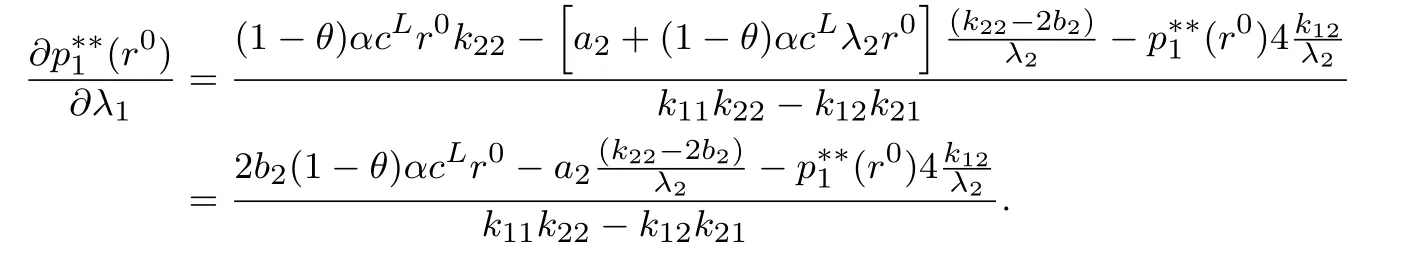
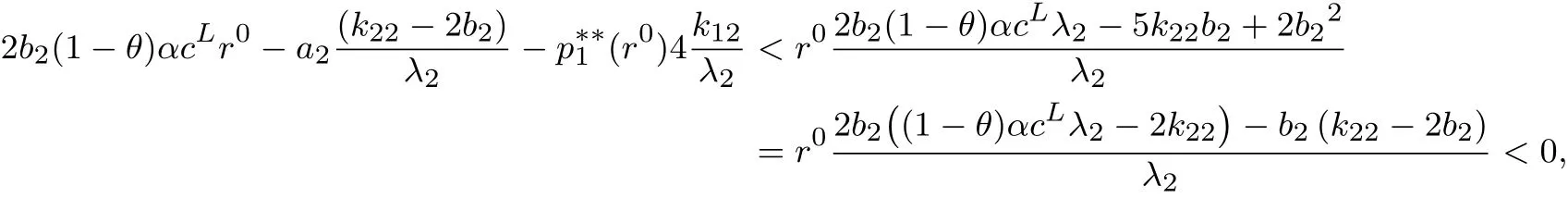
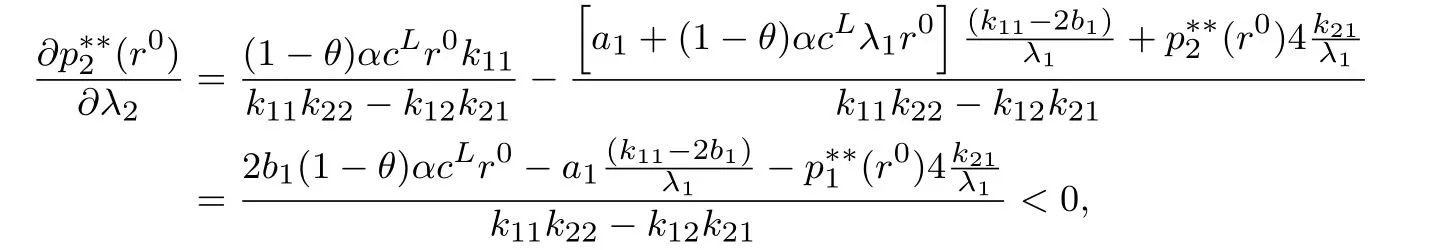
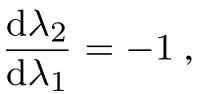
(Business School of Central South University,Changsha 410083,China)

