基于多目标进化算法的异步电动机现场效率测算
孙冠群,牛志钧,蔡 慧,王斌锐
(1.中国计量学院机电工程学院,浙江 杭州 310018;2.中国北车永济新时速电机电器有限责任公司,山西 永济 044502)
基于多目标进化算法的异步电动机现场效率测算
孙冠群1,牛志钧2,蔡 慧1,王斌锐1
(1.中国计量学院机电工程学院,浙江杭州310018;2.中国北车永济新时速电机电器有限责任公司,山西永济044502)
介绍了一种基于多目标进化算法(MOEAs)的异步电动机现场实时效率测定方法。通过对多目标算法进行优化、比较,提出使用非支配排序遗传算法Ⅱ(NSGA-II)和强度帕累托进化算法2(SPEA2)的低侵入式方法用于异步电动机效率估算,仅需电动机运行时通过传感器检测其实时转子速度和定子电阻,而无需拆下电动机或单独做一些实验项目来获取所需参数。通过5.5kW电动机的实践表明,该方法在估算异步电动机效率方面是有效的,尤其在常规的负载范围内,用该方法的估算值与实际试验值的误差小于3%;相互比较后发现,NSGA-Ⅱ方法的估计结果略优于SPEA2方法的结果。
计量学;异步电动机;多目标进化算法;非支配排序遗传算法Ⅱ;强度帕累托进化算法2;效率测算
1 引言
当前,在工业领域,如风机、水泵等驱动设备中的多数电动机是低效率运行的。因这些设备经常运行在额定负载以下,并不是在额定的最佳效率点运行;此外,由于老化问题,即使在额定状态下,其实际效率也小于实际值;随着节能减排的兴起,我国频繁更新发布日趋严格的能效指标(GB 18613—2002、2006、再到2012版)。综合以上3点,对现行使用的电动机进行效率测算,并逐步更换低效率运行和相对效率值低的电动机,是非常有实际意义的,并且最好是电动机运行期间测算其效率,否则很难精确证明它在使用中的效率状况。然而,探寻侵入性低、结果精确的异步电动机现场效率估算方法并不简单。本文针对最普遍使用的三相异步电动机的现场效率估算为研究对象。
文献[1]对众多的电机效率估算方法进行了分析,推荐了3种方法,分别为ORMEL96(等效电路法)、OHME(损耗分离法)、气隙转矩(AGT)法,这3种方法均可改善非侵入性,然而大多仅停留于理论上的分析。文献[2]给出了进化规划(EP)算法估算异步电动机的效率,但精确性不佳。文献[3]提出了一种混合效率估计方法,与遗传算法结合,也结合了气隙转矩法、损失分离法和等效电路法,在非侵入性、精确度上有所进步。总的来说,进化算法提供了非侵入式方式估计现场电机效率,只需利用电动机的输入值,不需要其输出值[4]。
非支配排序遗传算法Ⅱ(Non-dominated Sorting Genetic Algorithm-Ⅱ,NSGA-II)和强度帕累托进化算法2(Strength Pareto Evolutionary Algorithm-2,SPEA2)是多目标进化算法(Multi-objective Evolutionary Algorithms,MOEAs)中的2种,尤其是NSGA-II在电抗器导线质量与损耗优化、农作物灌溉水量与日期优化、火电厂经济配煤等方面多有应用成功案例[5~7],文献[8]也针对SPEA2的改进进行了研究。本文在应用NSGA-II和SPEA2时,同时也利用了ORMEL96和OHME方法,并对实测值与该混合方法下的现场估算值进行了比较。
2 多目标进化
多目标优化问题(MOPs)的一般定义为

式中,x为决策矢量集;X为决策空间;y为目标矢量集;Y为目标空间;g(x)和h(x)为决策变量约束条件。MOPs的解集由全部决策参数组成决定,对于相应的目标矢量,如果没有其他参数的劣化,就不能改善目标矢量值,这种解决方案被称为帕累托最优解,该解决方案能考虑到所有的目标值。考虑到问题的属性和特点的同时,关键是找到最优的折衷方案。
2.1NSGA-Ⅱ
NSGA-Ⅱ是德伯等人提出的一种快速的精英多目标遗传算法,依据精英策略,它通过后代选择算子的应用,保留传统最佳解决方案。
NSGA-Ⅱ的示意图见图1。
用N表示种群数量,Rt=Pt∪Qt是复合种群,大小为2N的种群Rt使用非支配排序。由于Rt囊括了初始(父代)种群和当前(子代)种群,精英策略可以实现。复合种群中非支配排序层F1为最优非支配层,F1含有占优解,F1层中的占优解必须相比复合种群中其他解更受到重视。如果F1的种群数小于N,F1层全部种群就会纳入新的种群Pt+1,Pt+1的其余的部分将按照等级顺序从后来的非支配层中选择,如此,下面是从F2中选择解,接着是从F3层,依次类推,这种步骤一直持续到随后的非支配层(组)为止,找到确切的N个解后,最后通过拥挤度比较降序排列,并选择所需的最佳解填补所有种群,获得新的Pt+1种群后,遗传算子通过选择、交叉、变种可以产生一个新的数量为N的Qt+1种群,基于拥挤比较算子的锦标赛选择方式作为选择解的方法[5]。

图1 NSGA-Ⅱ示意图
2.2SPEA2
Zitzler等人提出了基于SPEA的改进算法SPEA2。SPEA2有如下特点:
(1)使用一种改进的适应度分配方案,需要考虑到个体、支配多少个体以及本身的支配问题。
(2)使用近邻密度估计技术,允许更精确的搜索程序引导。
(3)使用一种新的档案截断方法,保证边界解的保留。
SPEA2算法简要概括为:为了计算解的适应度,无需帕累托排序,因为适应度基于强度值,基本上,解的强度值代表了解的数量,因此,一个过零值表示一个非支配解。SPEA2使用两种种群,初始种群和档案种群,迄今为止发现,档案种群保持着最好的非支配解。首先,一个初始种群是随机构成的,但档案是空的;其次,该算法在子代种群中计算解的适应度,并且全部非支配解包含在档案中,由于档案集合的规模是固定的,根据邻近距离一个截断算子排挤出部分解,免得解的数量超出预定义的限制,如果一些非支配解比预定的少,最小适应度值的支配解将进入档案中,然后,解的个数被确定,并采用二进制锦标赛交替选择进行重组,最后,利用选择、交叉、变异的遗传算子,创建一个新的种群,这个种群通过评价纳入档案[8]。
3 异步电动机效率现场估算的多目标进化算法
传统的绝大多数现场效率估算方法存在难于计算或需要付出较高的代价,有的根本不准确没实际意义。本文将等效电路方法、分离损耗方法和多目标进化算法均纳入异步电动机效率的估算上,这些方法可完全不用从应用现场脱开电动机,现场测试和估算也能保持较高的准确性,同时测算方法符合相关的GB和IEC标准。
3.1异步电动机等效电路模型
异步电动机考虑杂散损耗后的等效电路见图2,其中Rst为等效杂散损耗。

图2 异步电动机等效电路


Pst、Pfl分别为任意点杂散损耗和全负载杂散损耗;I2、I2fl分别为任意点转子电流和全负载时的转子电流。电阻Rst可以用下式计算
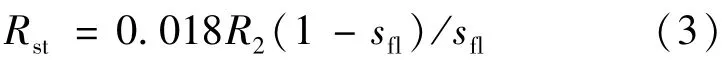
sfl为全负载的转差率,当电机转子速度达额定速度并且定子电压和电流也达额定值时计算的转差率s=sfl;定子线电阻在电动机停机后是可以测量的,则等效电路中的定子相电阻计算如下(三相绕组星形接法)

式中,R1l为定子线电阻。选择的电动机的定、转子电抗值之间的比例为x1/x2=1。

有效的转子导纳可以计算为
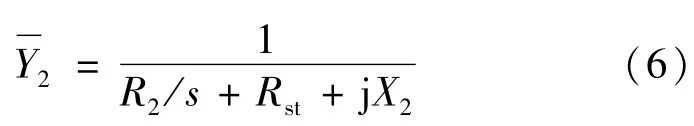
定子电流等于

转子电流为

励磁支路电流

输入功率为

受饮食习惯的影响,不同地区人均粮食消费标准有所不同,本文参照卢良恕[10]等按中国国情计算得出的人均消费400 kg粮食即可达到营养安全的要求。
3.2基于异步电动机效率估算的多目标进化算法
本文所采用的三相异步电动机,是按照GB 18613—2006二级能效标准设计的四极、机座号132的标准电机,铭牌数据分别为功率5.5 kW,电压380 V,交流频率50 Hz,额定转速1440 rpm,额定电流11.8 A,额定效率89.2%,额定功率因数0.83。
在第一阶段,定子绕组电阻R1,供电电压U1,定子绕组电流I1,速度n和输入功率Pi在不同负载点进行实际测量。输入功率因数的计算方法为

电动机停机后R1的值为3.17 Ω。表1为负载从50%到125%间电机的实测参数值,这些试验数据将被用来比较和验证后续所估算的效率值。

表1 三相异步电动机不同负载率时实测数据(f=50 Hz)
本文提出一种基于多目标进化算法的异步电动机效率获取方法,目标是使得实测与利用该算法的估算值之间的误差最小。定子电阻和电动机转子速度需要实际测量,实际中也可较为方便地获得(装设速度传感器)。最初,定子电阻R1和多目标进化算子的交叉率、变异率、种群规模和世代数量等均明确指定。使用随机生成的参数(X1,R2,Xm,Rm),该异步电动机效率即可通过NSGA-Ⅱ或者SPEA2算法确定。效率计算时,输入参数由输入功率和定子电流组成。
绝对误差函数为

如果将功率因数引入也作为一个约束条件,由于根据相关计算量预期过大,需增加种群数、计算更复杂、成本增加,不是较现实的方式,故予以舍弃。
在这一阶段,NSGA-Ⅱ或者SPEA2提供非支配解集用来作为优化技术解决上述的多目标问题,在帕累托最优集中的这些解是相当重要的。最终的解,是通过一个决策过程从众多解中进行选择,此决策过程需进行大量样本的学习训练,详见文献[9]。学习后确定的优选解是通过计算非支配解和最初解之间的欧几里德距离,即从帕累托最优集中选择,如当最优解在M优化中对应于零误差时,所选择的解将是具有最小的定子电流和输入功率误差值的解,利用最小化欧几里德距离仿真,通过欧几里德距离在帕累托最优集中进行解的选择,可应用于对异步电动机的效率进行计算。
具体来说,等效电路参数X1、R2和Xm被编码为10位无符号二进制数,Rm被编码为一个14位无符号二进制数,种群中一个染色体完全可形成44位字符串[10]。
确定NSGA-Ⅱ和SPEA2的各仿真参数为种群数=100,最大世代数量=100,变异概率=0.01,交叉概率=0.8,SPEA2的档案数=300。
总的来说,基于异步电动机的等效电路,利用已知供电电源参数和测算的实时速度值,可获取电机的转差率;利用测算的定子电阻及损耗分离方法,根据多目标算法多次学习生成等效电路中的其他参量并且可计算出电流、功率因数、输入输出功率等,从而最终获得效率的估算值。
4 实验结果
NSGA-Ⅱ和SPEA2用来确定电动机的现场实时效率值,在优化过程中获得的最大数量的一代可以考虑作为候选解。由于不同的算法及组合的运行,给出了不同的电动机的效率值,在不同负载点每种算法均运行5次,然后这些结果进行平均后,就被视为最后的解,实验中给出两种不同的方法。
4.1方法一
在此方法中,只有表1中的全负载时的实测数据(即100%额定负载)用于电机参数测定,等效电路参数X1、R2、Xm和Rm是通过MOEAs方法随机产生的,然后这些值用于计算不同负载点的定子线电流、功率因数、输入功率、输出功率和相应的效率值,这个过程执行5次,取平均值作为确定的效率值。计算值与实测数据比较,MOEAs与实测数据间在不同的负载点,其误差也是不同的,表2给出了所得到的结果,它利用M适应度函数,定子线电流和输入功率作为输入参数,图3则图解了不同负载率下NSGA-Ⅱ和SPEA2的误差。
4.2方法二
在此方法中,NSGA-Ⅱ和SPEA2运行5次,记录不同负载点的效率平均值,不同负载点的效率计算值与实测数据比较,通过利用适应度函数M,得出结果见表3,不同负载点的估算和实测效率曲线见图4。实验结果表明,与方法一比较,NSGA-Ⅱ的解略优于SPEA2的解;并且,75%负载点比其他负载点的误差要小。
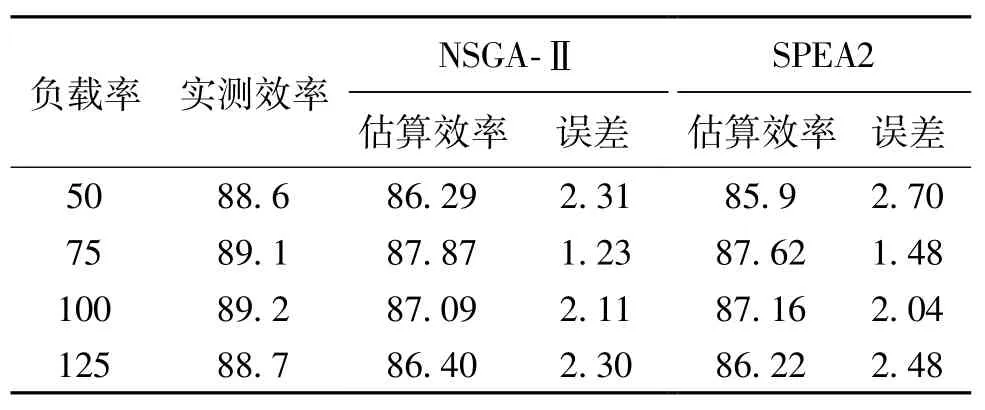
表2 方法一所得结果(%)

图3 方法一的不同负载情况下各算法效率走势
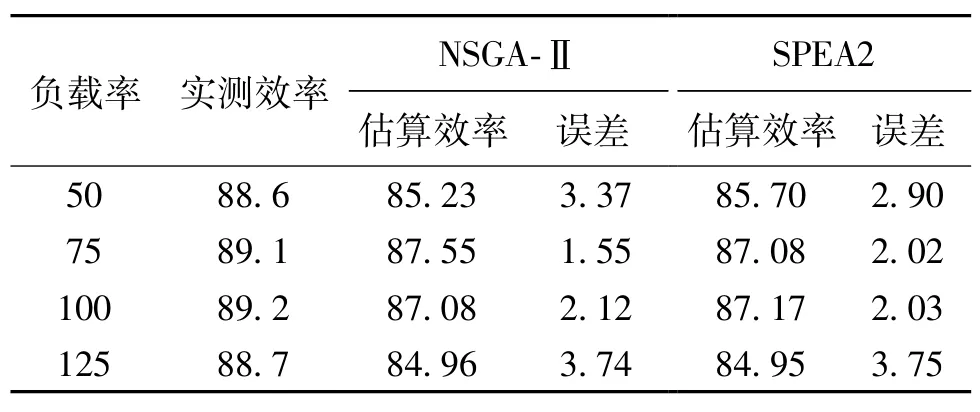
表3 方法二所得结果(%)

图4 方法二的不同负载情况下各算法效率走势
结果表明,所有的基于MOEAs估算出的效率值均收敛于实测的效率值,但效率误差在50%负载点高于其他负载点。低负载点的偏差的产生,主要是因为这时的多目标优化采用解析计算的方式。这表明,执行计算时,等效电路模型存在一些不足,在方法一中,仅仅满载实验数据被用在其他负载点的效率的计算上;在方法二中,在每个负载点该算法是单独运行的。方法二产生与方法一相同的结果。
5 结论
该方法仅需检测电动机的运行速度和定子电阻,便可较迅速地估算其效率值,无需从工作岗位上卸下电动机,也无需单独进行高精度的空载试验。本研究中,等效电路方法、分离损耗方法和MOEAs方法相互结合,均被纳入来确定异步电动机的效率。电动机正常运行时(负载范围大多从75%到100%的额定负载),估算的误差小于2%。一般来说,满载时,基于MOEAs的估算结果与实测结果最为接近,可见NSGA-Ⅱ和SPEA2算法可以找到比传统的优化方法更好的结果。一个重要原因是所得到的解并不依赖于加权过程中的权重向量,因为这个算法搜索同样的目标,可以更容易地获得帕累托最优解前沿。在低负载时(小于50%)给出的估算值误差较大,但由于实际中多数电动机往往运行在高于50%额定负载的情况下,本文的结果最终还是令人满意的。
[1]Lu B,Habetler T G,Harley R G.A survey of efficiency estimation methods of inservice induction motors[J].IEEE Trans Indus Appl,2006,42(4):924-933.
[2]Subramanian S,Bhuvaneswari R.Evolutionary programming based determination of induction motor efficiency[J].Electr Power Compon Syst,2006,34:565-576.
[3]Lu B,Cao W,French I,et al.Non-intrusive efficiency determination of in-service induction motors using genetic algorithm and airgap torque methods[C]//42nd IAS Annual Meeting,New Orleans,2007.
[4]Cunkas M,Sag T.In-situ efficiency determination of an induction motor using the multiobjective genetic algorithms [C]//16thinternationalsymposiumonintelligent manufacturing systems,Turkey,Adapazar,2008.
[5]张成芬,赵彦珍,陈锋,等.基于改进NSGA-Ⅱ算法的干式空心电抗器多目标优化[J].中国电机工程学报,2010,30(18):115-122.
[6]郄志红,韩李明,吴鑫淼.基于改进NSGA-Ⅱ的作物灌水量与灌溉日期同步优化[J].农业机械学报,2011,42(5):106-111.
[7]夏季,华志刚,彭鹏,等.基于非支配排序遗传算法的无约束目标优化配煤模型[J].中国电机工程学报,2011,31(2):85-91.
[8]章萌,章卫国,孙勇.多目标强度Pareto混沌差分进化算法[J].控制与决策,2012,27(1):41-48.
[9]Chen T Y,Hsu Y S.A multi-objective optimization solver using rank-niche evolution strategy[J].Adv Eng Soft,2006,37(3):684-699.
[10]Sag T,Cunkas M.A tool for multi-objective evolutionary algorithms[J].Adv Eng Soft,2009,40(9):902-912.
In-situ Efficiency Measurement of Induction Motor Based on MOEAs
SUN Guan-qun1,NIU Zhi-jun2,CAI Hui1,WANG Bin-rui1
(1.College of Mechanical and Electrical Engineering,China Jiliang University,Hangzhou,Zhejiang 310018,China;2.Yongji Xinshisu Electric Equipment Co Ltd,CNR Group Corporation,Yongji,Shanxi 044502,China)
A method based on multi-objective evolutionary algorithms(MOEAs)for real-time and in-situ efficiency determination of induction motor is introduced.The multi-objective algorithm is optimized,and it introduces a low-intrusive level method based on non-dominated sorting genetic algorithm-II(NSGA-II)and strengths Pareto evolutionary algorithm2 (SPEA2)for efficiency estimation of the induction motor.Therefore,the equivalent circuit method,and the segregated losses method combine with MOEAs.Through the practice of a 5.5 kW motor,it shows that,the method on the estimation of induction motor efficiency is effective,and in the normal range of the load,the estimating value and the actual value of test error is less than 3%.And compared to each other,it is found that NSGA-Ⅱresults are slightly superior to that of the SPEA2.
Metrology;Induction motor;Multi-objective evolutionary algorithms;Non-dominated sorting genetic algorithm-Ⅱ;Strength Pareto evolutionary algorithm-2;Eefficiency measurement
TP971
A
1000-1158(2015)01-0087-05
10.3969/j.issn.1000-1158.2015.01.19
2012-10-18;
2014-08-22
国家自然科学基金(50905170);浙江省教育厅项目(Y201018995)
孙冠群(1974-),男,河北涞水人,中国计量学院讲师,研究方向为电机及其控制与检测。Sgq741129@126.com

