石英晶体微天平质量检测量研究

陈 艳，黄显核

（1.西南科技大学信息工程学院，四川　绵阳　621010；2.电子科技大学自动化工程学院，四川　成都　610054）

石英晶体微天平质量检测量研究

陈 艳1，黄显核2

（1.西南科技大学信息工程学院，四川绵阳621010；2.电子科技大学自动化工程学院，四川成都610054）

基于石英晶体微天平质量检测原理，通过分析石英谐振器表面的振动位移，得出决定其电极表面每一点处质量灵敏度的物理量为该点处的振动加速度。在此基础上，基于石英谐振器的巴特沃斯-范·戴克等效电路模型提出一种计算石英晶体谐振器表面振荡幅度的方法，最终得到石英晶体微天平在整个检测过程中能检测到的平均质量。用10 MHz的石英晶体微天平进行了数值验证，计算值与其理论上能达到的pg级检测限基本相吻合。

计量学；质量检测量；振动加速度；石英晶体微天平

1　引言

石英晶体微天平（Quartz Crystal Mircrobalance，QCM）是一种在20世纪60年代兴起的新型超灵敏微小质量传感器，现已在物理、化学、生物、医学等学科的检测问题中得到了广泛应用［1～5］。QCM利用石英晶体的压电效应实现晶片电极表面的质量变化量到谐振频率变化量的转换，其检测限理论上可达到pg级，目前已达到ng级，而当前通用的电子微天平的检测限则只能达到μg级。对于QCM的检测灵敏度比通用电子微天平高出如此之多的原因，研究者至今没有给出物理方面的解释。随着谐振器振动频率的变化、晶片表面电极形状的改变以及电极尺寸的不同，QCM电极表面中心处能够检测到的质量会随之变化，从而导致整个QCM检测过程中平均能够检测到的质量发生变化。因此，使得其质量检测量难以获取。

针对QCM检测过程中，在不同电极大小、不同电极形状和不同振荡频率情况下，其质量检测量会发生变化的特点，首先对石英表面的振动位移进行分析。根据QCM质量灵敏度分布的特殊性，借助石英谐振器的巴特沃斯-范.戴克（BVD）等效电路模型获得QCM在整个检测过程中能检测到的平均质量。在此基础上，采用唐山晶源裕丰电子股份有限公司的10 MHz QCM进行实验验证。

2　QCM质量检测原理

QCM由具有零温度频率系数的AT切石英晶体构成，谐振器的振动模式为厚度剪切振动模式。对于厚度切变模式的石英晶片，当石英晶片的直径远大于厚度时，石英谐振器的频率方程为［6］：

其中：d为石英晶片的厚度，cm；ρq为石英晶体的密度，g·cm-3；μq为石英晶体的压电强化剪切模量，g·cm-1·s-2；n为泛音次数。

当外来物附着在石英晶体电极表面时，设在有效面积上的附加质量为Δm，引起的频率变化为Δf，引起的石英晶片的厚度变化为Δd，则由式（3）可得：

由式（3）和式（4）可得：

联合式（1）和式（5），在Δd≤d时，有：

而Δm与Δd有以下关系：

其中：S为石英电极的面积，cm2。

联合式（2）、式（3）、式（6）和式（7），并结合石英晶体谐振器的泛音频率fn与基频f0的关系即可得经典的Sauerbrey方程：

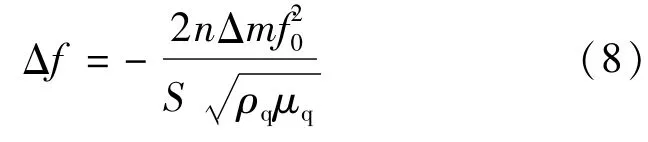
式（8）表明QCM电极表面微量物质质量的变化量都可以通过谐振频率相应的变化量来识别，且QCM的质量灵敏度Δf/Δm与石英谐振器频率的平方成比例。

3　理论推导

QCM的质量灵敏度关系到其检测的准确性，检测的灵敏度越高，它就越能够检测到石英晶片上极微小的质量变化。

3.1QCM质量灵敏度

QCM质量灵敏度与谐振器振动幅度分布相同，且都为高斯分布［7～10］：

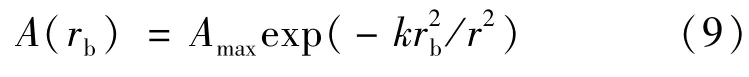
式中：Amax为谐振器的振动幅度，10-10m；k为无量纲的常数，决定了高斯分布中峰值的宽度，k越大，峰值的宽度越窄；r为石英晶片表面电极的半径，cm；rb为离电极中心处的距离，cm。另外，由于谐振器的交流电压与振动幅度成比例［11］，因此QCM质量灵敏度与谐振器振动幅度分布可用图1表示。

图1　质量灵敏度相关的Δf和振动幅度相关的U分布

谐振器振动时，任意振动点的位移x为：

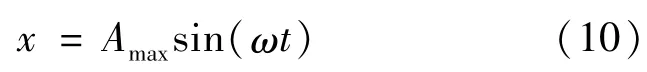
则该振动的加速度为：

由式（8）和式（11），并结合图1可以得出：决定QCM电极表面每一点处质量灵敏度的物理量为该点处的振动加速度，且在电极中心处加速度最大为ω2Amax，即在电极中心处QCM质量灵敏度最大。

3.2QCM质量检测量

QCM与广泛使用的电子微天平具有同一特点：最小检测量与施加于该质量上的加速度的乘积是一常数［12，13］，大约为10-9kg·m·s-2，因此：

QCM最小测量质量直接决定了它的应用领域，因此获取QCM最小测量值的方法变得至关重要。由以上分析可知，QCM用于微量物检测时，只要能够确定石英晶片电极中心处的振动幅度，即可算出中心处的加速度，从而能够确定检测中的最小测量值。然而，在用QCM进行实际的检测过程中，不能保证把外来微量物准确地附着于电极中心处，因此只获取电极中心处微量物的振动幅度对整个检测过程还远远不够，还需要获得整个石英电极表面的平均振动幅度，从而获取QCM能够检测到的平均质量。下面将重点研究整个石英电极表面的平均振动幅度。

3.3QCM电极表面振动幅度计算理论推导

计算QCM谐振器的振荡幅度有很多方法，比如静态位移的谐振放大。然而静态位移的谐振放大在计算过程中需要获取QCM检测中石英谐振器的品质因数Q值，而QCM工作过程中品质因数的获取是很困难的，因此，这里引入利用石英谐振器的BVD等效电路模型来计算QCM谐振器的振荡幅度。QCM在质量负载和液体阻尼负载共同作用下的等效电路如图2所示［15］。为了简化分析过程，将图2简化为图3。

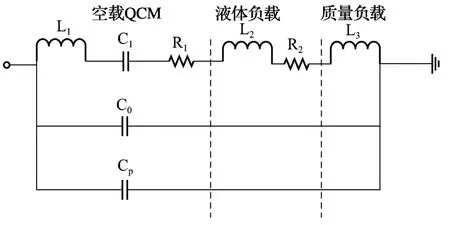
图2　QCM工作于质量负载和液体阻负载的等效电路

图3　QCM简化等效电路

简化后的等效电路由两条支路够成：动态支路（R，C，L）和静态支路（C*）。动态支路中的R不仅与石英晶片表面的电极大小有关，而且还与QCM工作过程中能量的损耗有关。电极面积越大，R越大；谐振器的损耗越大，表明R越大，因此R包含了QCM工作过程中，谐振器的所有能量损耗。由于QCM在实际的应用过程中，谐振器的频率都不太高，一般都在10 MHz以内，且C*的值一般也比较小，所以QCM等效电路的阻抗可以近似表示为：

采用压电电流密度计算谐振器振动时的幅度是为了消除电极尺寸对电路性能的影响。因此对压电电流密度在1/4个周期内积分就可以将其转化为压电极化P为：

由P=ex即可获得应变x，其中e为压电极化系数［16］。最后，压电位移即谐振器的平均谐振幅度为：

若需要在已知谐振器的平均谐振幅度的前提下获得电极中心处的最大振动幅度，则变得非常容易，利用式（9）：

因此，石英晶片电极中心处运动的最大幅度为：

4　实验验证

实验首先选用工作于厚度剪切模式下的AT切石英晶体谐振器，振荡频率为10 MHz，晶片表面上电极面积为0.114 cm2，晶片厚度为0.016 8 cm。将其用于气相检测时，用网络分析仪E5062A测得等效电路中的R为44.4 Ω。

当石英晶片两端输入峰峰电压为0.4 V时，由式（14）可得QCM的压电电流密度Jcd为

由式（15）可知压电电流密度转化为压电极化P（单位为C/cm2）的值为

结合式（16）可得谐振器的平均谐振幅度：

取高斯分布中的k值为1.7，再结合式（18）可得石英晶片电极中心处的最大振动幅度为：

则谐振器振动时石英晶片电极表面的平均加速度与电极中心处的最大加速度分别为：

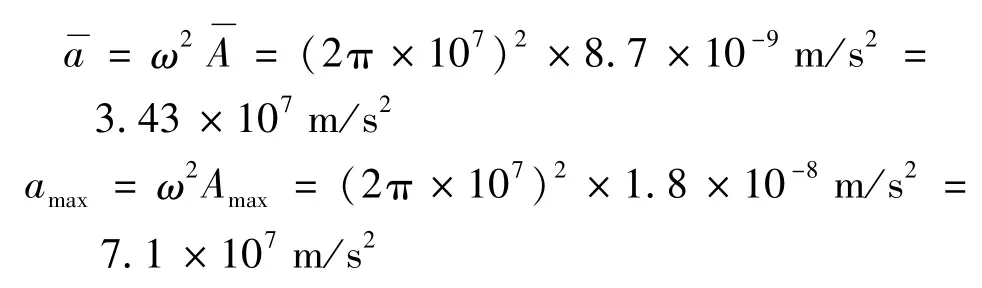
结合式（12）可得QCM在检测过程中能够检测到的平均质量和最小可检测到的量分别为

实验结果与QCM理论上能达到的pg级检测限基本吻合。

5　结论

计算所得QCM能够检测到的平均质量与理论检测限相比较，尽管存在一定的误差，但已达到pg级，表明通过计算QCM谐振器表面的振荡幅度来获得QCM的平均质量检测量是可行的。实验中存在一定误差的原因是晶片表面电极的质量负载因子过大，从而导致了高斯分布的质量灵敏度曲线比较尖锐。石英晶体微天平质量检测量的研究为其在新领域的应用打下了一定的理论基础。

［1］Marx K A.Quartz Crystal Microbalance：A useful tool for studying thin polymer films and complex biomolecular systems atthesolution-surfaceinterface［J］.Biomacromolecules，2003，4（5）：1099-1120.

［2］Johannsen K，Page D，Roy S.A systematic investigation of current efficiency during brass deposition from a pyrophosphate electrolyte using RDE，RCE，and QCM［J］.Electrochimica Acta，2000，45：3691-3702.

［3］Chen Y，Huang X H，Shi H S，et al.A novel and costeffective method for early lung cancer detection in immunized serum［J］.Asian pacific journal of cancer prevention，2011，12（11）：3009-3012.

［4］Chen Y，Huang X H，Shi H S，et al.Rapid detection of ovarian cancer from immunized serum using a quartz crystal microbalance immunosensor［J］.Asian pacific journal of cancer prevention，2012，13（7）：3423-3426.

［5］Du B，Johannsmann D.Operation of the quartz crystal microbalanceinliquids：derivationoftheelastic compliance of a film from the ratio of bandwidth shift and frequency shift［J］.Langmuir，2004，20（7）：2809-2812.

［6］秦自楷.压电石英晶体［M］.北京：国防工业出版社，1980，129-132.

［7］Sauerbrey G.Messung von plattenschwingungen kleiner amplitude durch lichtstrommodulation［J］.Zeitschrift for Physik A Hadrons and Nuclei，1964，178：291-295.

［8］Schneider T W，Martin S J.Influence of the compressional wave generation on thickness-shear mode response in a fluid［J］.Anal Chem.1995，67：3324-3335.

［9］Lucklum R，Hauptmann P.Determination of polymer shear modulus with quartz crystal resonators［J］.Faraday Discuss，1997，107：123-140.

［10］Richardson A，Bhethanabotla V R，Smith A L，et al.Patterned Electrodes for Thickness Shear Mode Quartz ResonatorstoAchieveUniformMassSensitivity Distribution［J］.IEEE Sensors journal，2009，9（12）：1772-1777.

［11］BenesE.Improvedquartzcrystalmicrobalance technique［J］.Appl Phys，1984，56：608-626.

［12］Mecea V M.Is quartz crystal microbalance really a mass sensor？［J］.Sensors and Actuators A，2006，128：270-277.

［13］Mecea V M.Fromquartzcrystalmicrobalanceto fundamental principles of mass measurements［J］.Analytical Letters，2005，38（5）：753-767.

［14］Borowsky B，Mason B L，Krim J.Scanning tunnelling microscope measurements of the amplitude of vibrations of a quartz crystal oscillator［J］.Appl Phys，2000，88：4017-4021.

［15］Martin S J，Granstaff V，Frye G C.Characterization of a Quartz Crystal Microbalance with Simultaneous Mass and Liquid Loading［J］.Anal Chem，1991，63（20）：2272-2281.

［16］叶会英，禹延光.压电参数的光反馈干涉测量方法［J］.计量学报，2008，29（4）：349-352.

Study on Mass Detectable Quantity of Quartz Crystal Microbalance

CHEN Yan1，HUANG Xian-he2
（1.School of Information Engineering，Southwest University of Science and Technology，Mianyang，Sichuan 621010，China；2.School of Automation，University of Electronic Science and Technology of China，Chengdu，Sichuan 610054，China）

The vibrational displacement on crystal surface is analyzed on the basis of mass detection principle of quartz crystal microbalance，leading to the conclusion that the physical quantity which determines the mass sensitivity in every point on the electrode surface of the crystal is the acceleration of the crystal vibration in that point.Based on this conclusion，the Butterworth-Van Dyke equivalent circuit of crystal resonator was employed to obtain the computational method of oscillation amplitude on the surface of the quartz crystal microbalance resonator，thus obtaining the average detectable mass of quartz crystal microbalance in the overall detection process.The experimental result was generally in line with theoretical value（at the picogram level）when experimented on a 10 MHz quartz crystal microbalance.

Metrology；Mass detectable quantity；Vibration acceleration；Quartz crystal microbalance

TB932

A

1000-1158（2015）01-0063-04

10.3969/j.issn.1000-1158.2015.01.14

2012-10-18；

2013-04-06

中央高校基本科研业务费基金（ZYGX2012YB030）

陈 艳（1981-），女，四川雅安人，西南科技大学教师，主要从事压电免疫传感器方面的研究。yanchencd@163.com