传热管道设备的内壁状态监测方法

张玉存，周 珊，魏斌，付献斌

（燕山大学，河北　秦皇岛　066004）

传热管道设备的内壁状态监测方法

张玉存，周 珊，魏斌，付献斌

（燕山大学，河北秦皇岛066004）

在特定边界条件下对热传导方程进行求解，优化所得温度分布方程的系数，并利用分段积分法对系数进行化简，建立了传热管道设备表面温度、材料特性与内壁状态3者间的关联模型，并将其应用在传热管道设备的内壁状态监测上。结合导热反问题，利用所建立的关联模型分析传热管道设备外表面的温度数据，得到内壁几何形状。通过仿真实验验证了该方法的可行性，从而为传热管道设备内壁状态的实时监测提供依据。

计量学；导热反问题；内壁状态；缺陷检测；传热管道设备

1　引言

由于传热管道设备的内壁长期处于高温、高压及介质冲刷等恶劣的工作条件下，容易产生应力、腐蚀破裂等现象，形成内部缺陷或故障，给安全生产带来隐患。在生产过程中及时准确地对缺陷的位置、几何尺寸做定量分析，确定其严重程度，能够及时发现传热管道设备内部的异常和早期疲劳损伤的情况，可为设备的正常运行提供保障。

针对工业热设备缺陷的无损检测国内外众多学者已进行了深入研究。Hsieh C K等采用数值计算方法建立了用于求解单层三维筒状设备内壁缺陷的解析理论［1］。Sahnoun S等利用二维模型对平板结构内的圆形缺陷进行了红外无损检测，确定了缺陷的位置及性质［2］。Huang C H等将共轭梯度法应用于二维平板边界的识别［3］。Sakagami T等采用脉冲加热的方法对工业材料内部的缺陷进行检测，能够比较精确地检测缺陷的尺寸和方位［4］。Chen Cha＇o-Kuang等利用有限差分法和重排矩阵法，实现了根据双层炉膛外表面温度分布对内壁面几何边界的监测［5］。张建涛等采用共轭梯度法建立二维的缺陷检测模型［6～8］。冯立春等对红外热波无损检测技术进行了深入的研究和实验，使检测时间大大减少［9］。宋利明、曹春梅等将更加完善的解析方法应用在二维双层球壳和筒状工业热设备内壁缺陷的检测上［10～12］。

本文在Hsieh C K、宋利明等人的基础上，对导热反问题的解析方法进行进一步研究，利用边界条件优化温度分布方程的系数，并采用分段积分法对系数进行化简，从而建立传热管道设备表面温度、材料特性和内壁状态3者之间的关联模型。在对传热管道设备外表面最大温差的影响因素进行研究的基础上，应用所得关联模型对具有一定内壁缺陷的传热管道设备进行分析，从而实现对缺陷位置和几何形状的定量分析。

2　传热管道设备内壁状态监测模型

图1为内壁破损的传热管道设备示意图。任取两截面S1、S2，由于它们远离破损区，认为在轴向是绝热的。S3为外表面，它向温度为T∞的环境对流散热；S4为内表面（温度为T0），其形状是待求的；S′4为假想的内表面［13，14］。

温度控制方程为如下拉普拉斯方程

边界条件

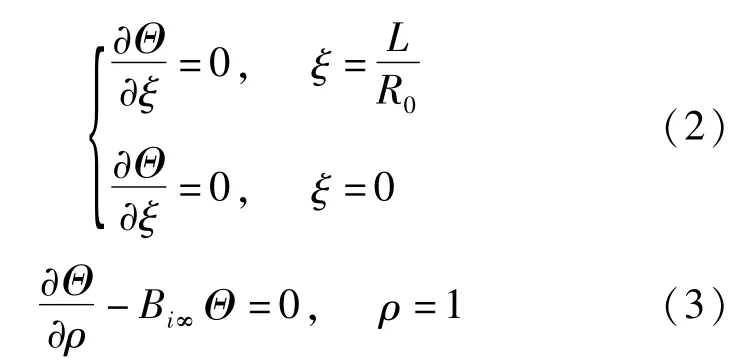
图中和式中，R0为圆柱外壁半径；L为圆柱轴向的长度；r为圆柱内任意处半径；φ为缺陷方位角；l为圆柱内任意处轴向长度；T∞为环境温度；T0为圆柱内壁温度；T为圆柱内任意点温度；k为热传导系数；h∞为外表面对流换热系数；Θ=（T-T∞）/（T0-T∞）为无量纲温度；ρ=r/R0为圆柱无量纲半径；ξ= l/R0为圆柱轴向的无量纲长度；Bi∞=R0h∞/k为毕奥准数。

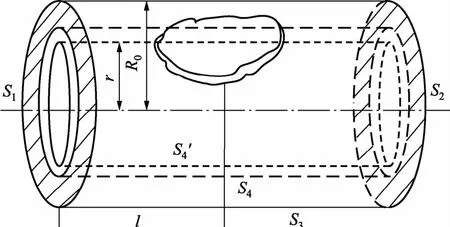
图1　内壁破损的传热管道设备示意图

采用分离变量法对以上方程进行求解，在内壁为等温边界条件时，管道内任一点的无量纲温度Θ（ρ，φ，ξ）=1。同时利用边界条件式（3）进行化简，可得到管道设备表面温度—材料特性—内壁状态3者间的关联模型为

式中，F′0，A′n，B′n，A″n，B″n，In，Kn，I′n，K′n系数均由传热管道设备外表面的温度决定。

由于传热管道设备的轴向长度远大于截面尺寸，可以只考虑圆周方向，并将管道设备外表面一个圆周上的N点离散温度Θ（1，φi）=ai，i=1，2，…，N，作为附加条件按方程Θ（1，φi）=Θi（cos nφ，sin nφ）进行形式拟合，同时令

则式（4）化简为

利用分段积分法对式（5）的系数进行化简，得到最终的传热管道设备表面温度—材料特性—内壁状态间的关联模型为

式中，ai（i=1，2，…，N）为外表面一个圆周上的N点离散温度值。通过计算机仿真可以得到内壁面每个离散角度φi对应的半径ρi，从而得到传热管道设备内壁的几何形状。

3　实验

3.1关联模型的影响因素

在Comsol Multiphysics仿真软件中建立如下模型：传热管道的内、外半径分别为0.436 5 m，0.368 m，导热系数为21.9 W/（m·K），外壁对流换热系数为20 W/（m2·K），内部流体温度为596 K。建立的传热管道形状见图2，得到的传热管道外表面温度分布情况见图3。

图2　试件内壁缺陷的形状

利用Comsol Multiphysics仿真软件在上述模型中设定不同的缺陷深度，可以得到外表面最大温差数值的变化曲线，见图4。由图4可以看出，在其他条件不变时，检测到表面的最大温差越大，表示试件内部缺陷深度越大。

同理，将上述模型中的其它参数固定不变，分别改变试件外表面对流换热系数、试件导热率以及缺陷的大小，可得如下结论：（1）试件导热系数越小、外表面对流换热系数越大，形成的外表面最大温差越大；（2）试件内壁的缺陷深度越大、面积越大，形成的外表面最大温差越大。

图3　试件外表面温度分布

图4　试件外表面最大温差随缺陷深度的变化

3.2利用关联模型求解内壁半径

在对具有特定缺陷的传热管道设备外表面最大温差影响因素进行研究的基础上，按照核电主管道的特性在Comsol Multiphysics仿真软件中建立模型，得到其外表面的温度分布。接着，利用Matlab软件将传热管道设备表面温度—材料特性—内壁状态间的关联模型应用到对设备内壁缺陷的分析中。

在Comsol Multiphysics仿真软件中建立传热管道类设备的模型：其外径为0.873 m，壁厚为0.068 5 m，材料为316 LN超低碳奥氏体不锈钢，其热传导系数为14.26 W/（m·K），外壁对流换热系数为20 W/（m2·K），内部流体的温度为596 K。得到管道外表面的温度分布后，等间隔地提取某一轴向长度上20个点的温度数据，利用Matlab软件根据所建立的关联模型分析所得温度数据，从而得到这个轴向长度上管道的内壁几何形状。

利用Comsol Multiphysics软件仿真设定了内壁分别为平缓减薄和突然减薄两类缺陷，见图5（a1）中采样得到缓慢升高的温度时，内壁为平缓减薄缺陷；图5（a2）采样得到突然升高的温度时，内壁为突然减薄缺陷。图5说明温度的异常升高情况，能够反映内壁减薄缺陷的大小，温度变化平缓时内壁缺陷变化平缓，温度发生较大变化时对缺陷的诊断出现波动。图5（b）为管道外表面某一轴向长度上，当温度分布为a图时，其内壁缺陷几何形状为相应的b图。分析图5（b）中不同曲线的数据得到管道某一轴向长度上的内径测量绝对误差分析表，见表1。

图5　管道外表面某一轴向长度上的温度分布与内壁缺陷几何形状图

表1　管道某一轴向长度上的内径测量绝对误差分析表

表中内径测量绝对误差的单位为m，通过计算得到内径测量的最大相对误差为0.938％，最小相对误差为0.046％，说明该模型在一定误差范围内，能够通过外表面温度的变化来反映出内壁缺陷的几何形状。

3.3利用关联模型监测内壁状态

取传热管道的轴向长度为1 m，其余参数与3.2节中设定的相同。当试件内壁为平缓减薄的圆形缺陷且缺陷最大深度设定为壁厚的37.9％时，对其外表面温度分布与内壁缺陷形状之间的关系进行研究。用不同轴向长度圆周上的温度分布曲线图对管道设备外表面展开后的温度分布进行表示，见图6。

由图可以看出，试件轴向长度为0.32 m到0.68 m的一段出现了局部的温度升高。结合传热管道设备表面温度—材料特性—内壁状态间的关联模型利用matlab软件对所得温度数据进行分析，得到试件轴向长度为l的圆周上，不同角度上的内径变化，部分数据见表2。

由表2可以看出，在这段试件上出现了很多内径大于试件标准内径的点（在表中用黑体做出标记），用不同轴向长度圆周上的内半径变化曲线图对管道设备的内径变化进行表示。

图7为不同轴向长度圆周上的内半径变化曲线图，由图可以看出，试件长度为0.32 m到0.68 m的一段产生了局部的内径增大。任意截面上的内径随角度的增加有先增加再减小的趋势，表示管道设备内表面具有破损的缺陷。结合图6的温度分布曲线图，当温度变化较大时，对内径的诊断出现波动。

图6　不同轴向长度上的外表面温度分布曲线图

表2　试件不同轴向长度上的内半径变化数值表m

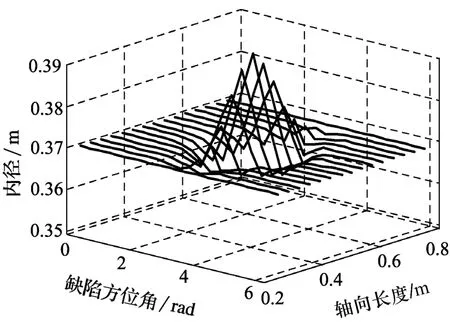
图7　不同轴向长度圆周上的内半径变化曲线图

仿真设定的管道破损最深处缺陷深度为标准壁厚的37.96％，利用本文所建立的关联模型得到的管道破损最深处内半径为0.391 8 m，内径测量的相对误差为0.558 4％。管道实际破损处的位置是0.32 m到0.68 m之间，与实验测得的破损位置一致。说明该模型在一定误差范围内，能够通过外表面温度的变化，反映出内壁缺陷的形状。

4　结论

本文建立了传热管道设备表面温度—材料特性—内壁状态3者间的关联模型，并对传热管道设备表面最大温差的影响因素进行研究。在此基础上，应用所得关联模型对具有一定内壁缺陷的传热管道设备进行分析。通过仿真实验证明了运用本文提出的方法能够准确实时地对缺陷位置和几何尺寸进行定量分析，且通过此方法降低了解析方法计算的复杂性，减小了求解傅里叶系数的准确性、内表面形状突变这两个因素对检测结果的影响。因此将该方法应用到传热管道设备内壁状态的监测中，能够及时发现设备内壁的异常情况，为设备的正常运行提供保障。

该方法也可应用于高温窑炉、高温反应设备、石油化工系统中的化学反应塔，联合循环电厂中的热交换器等筒状热设备内壁缺陷或故障的监测。通过红外热像仪获取设备外表面的温度分布数据，并对所得的温度数据进行分析，从而得到设备内壁缺陷的位置和形状。

［1］Kassab A J，Hsieh C K.Solution of the inverse geometric problem for the detection of subsurface cavities by the IRCAT method［J］.Rev Sci Instrum，1997，58（1）：33-65.

［2］Sahnoun S，Belattar S.Thermal non destructive testing study of a circular defect in plane structure［J］.British Journal of NDT，2003，8（8）：115-121.

［3］Huang C H，Chaing M T.A three-dimensional inverse geometryprobleminidentifyingirregularboundary configurations［J］.International Journal of Thermal Sciences，2009，48（3）：502-513.

［4］Sakagami T，Kubo S.Applications of pulse heating thermography and lock-in theromography to quantitative nondestructive evaluations［J］.InfraredPhysics& Technology，2002，43（4）：211-218.

［5］Cha＇o-Kuang Chen，Chin-Ru Su.Inverse estimation for temperatures of outer surface and geometry of inner surface of furnace with two layer walls［J］.Energy Conversion and Management，2008，49（2）：301-310.

［6］苟小龙，张建涛，王广军.基于导热反问题的管道内部缺陷诊断［J］.重庆大学学报（自然科学版），2010，32（2）：42-46.

［7］范春利，孙丰瑞，杨立.边界形状的红外识别算法［J］.化工学报，2010，61（11）：83-88.

［8］张有为，李辉，姜培学.采用共轭梯度法的管内壁温度导热反问题求解［J］.工程热物理学报，2009，30 （7），1188-1190.

［9］冯立春，陶宁，徐川.锁像热像技术及其在无损检测中的应用［J］.红外与激光工程，2010，39（12），1120-1123.

［10］王清秀，宋利明，杨泽宽.三维圆柱体系红外CAT解法［J］.冶金能源，1995，14（2）：45-49.

［11］关荣华，于慧.对圆柱型设备内壁缺陷的红外热诊断实验［J］.激光与红外，2002，32（1）：37-39.

［12］康文秀.两层介质圆筒热设备运行状态的红外监测［J］.激光与红外，2009，39（10）：68-69.

［13］奥奇西克M N.热传导［M］.俞昌铭，译.北京：高等教育出版社，1983.

［14］田立平.数学物理方程及其反问题研究［M］.北京：机械工业出版社，2010.

An Inner Wall Condition Monitoring Method for the Heat-transfer Pipe Equipment

ZHANG Yu-cun，ZHOU Shan，WEI Bin，FU Xian-bin

（Yanshan University，Qinhuangdao，Hebei 066004，China）

The heat conduction equation is solved under specific boundary conditions.The optimized coefficients of the resulted temperature distribution equation are simplified with the piecewise integral method，so the associated model of the heat-transfer pipe device is established.The relationship of the surface temperatures，the material properties and the inner wall condition of the heat-transfer pipe equipment is described in the associated model.And this model is applied in the inner wall condition monitoring for the heat-transfer pipe equipment.Combining with the inverse heat conduction problem，the surface temperature data is analyzed with the associated model to get the inner wall geometrical shape.The feasibility of this method is verified by simulation experiment.This method also provides a basis for the real-time monitoring of the heattransfer pipe's internal condition.

Metrology；Inverse heat conduction problem；Inner wall condition；Defect detection；Heat-transfer pipe equipment

TB942

A

1000-1158（2015）01-0031-06

10.3969/j.issn.1000-1158.2015.01.08

2013-03-28；

2014-10-23

国家重大科技专项基金（2011ZX04002-101）

张玉存（1969-），男，河北秦皇岛人，燕山大学教授，主要从事信号处理和光学测试研究。oldzhang@ysu.edu.cn