超球形分布式多播密钥更新方法研究

杨 帆

（安徽商贸职业技术学院电子信息工程系，安徽芜湖241002）

超球形分布式多播密钥更新方法研究

杨 帆

（安徽商贸职业技术学院电子信息工程系，安徽芜湖241002）

提出了一种超球形的分布式安全多播密钥管理方案。该方案充分利用了分布式多播中成员之间既独立又协同的特点，解决了安全多播密钥的更新问题，更新效率较高，有效地降低了组密钥更新的通信开销，且不增加计算开销和存储开销，并能很好地保证更新时的前向安全性和后向安全性。

分布式多播；安全多播；密钥更新；超球形

目前，分布式多播密钥管理方案或多或少都存在一些问题，如：在Clique［1］方案中，由于组密钥是基于Diffie-Hellman［2］算法产生的，密钥传输是线性的，故这种方案存在密钥存储量、计算量和通信量的数量级偏高的问题；基于树型的TGDH［3］密钥管理方案虽然较Clique方案在上述几个方面问题有所改进，但是它存在树状结构不平衡的缺点，当节点分布极度不平衡时，这种方案会变成线性的形式。

对集中式的密钥管理方案，文献［4］提出了一种超球形的密钥组织方式，文献［5］提出了一种M维几何球形组播密钥批量更新方案，它们的实质都是在集中式密钥管理的基础上引入了超几何体。在分布式多播中，由于组密钥是由成员共同参与产生的，协同性和独立性更加突出，更加适合利用超球模型来进行密钥的组织和管理，因此笔者将超球模型引入到分布式多播中，提出一种基于超球模型的分布式安全多播密钥管理方案。

1 密钥管理机制

先假设需要进行多播通信的节点有n个，将节点按照一定的规则进行分组，每组m个，根据每组节点的坐标可确定M维超球模型的球心及其半径，该球心即为这m个节点的父节点，再将这些父节点按m个一组进行划分，再次产生父节点，按此规则继续划分，直至产生根节点为止，这个根节点的坐标就是超球模型的超级球心的坐标，最后计算出的半径就是n个成员的组密钥。可以看出，任意一个节点的变化，都会影响其所在球的球心及与其相关联的所有球的球心坐标，而其他球的球心不受影响。为了保证分布式多播的前向和后向安全性，组成员发生变化时需要进行组密钥的更新。完成一次组密钥更新的过程是：通过某些组成员对组密钥加密后，再将密钥发送给多播组中剩余的成员，这些成员用解密密钥就可计算得到新的组密钥。

1.1 组密钥的生成机制

组成员相互协商可以产生一个共同的密钥，也就是说，不同的分布式多播组能够安全地协商出一个共同的加密密钥。设节点被分成4个多播组L、R、N、S，L的发起人是ML，密钥加密密钥是KL，R的发起人是MR，密钥加密密钥是KR，N的发起人是MN，密钥加密密钥是KN，S的发起人是MS，密钥加密密钥是KS。这里，对任意以非叶子节点（包括最顶节点）为根节点的子树，可选择其中一个叶子节点作为该子树的发起人。这4个小组通过如下步骤产生一个共同的组密钥。

1）ML、MR、MN、MS根据自身的坐标，计算出共同的球心，然后计算出这个球的半径，即组密钥K。

2）ML通过KL加密K并把它多播给L中的其他成员，MR通过KR加密K并把它多播给R中的其他成员，MN通过KN加密K并把它多播给N中的其他成员，MS通过KS加密K并把它多播给S中的其他成员，直到多播组L、R、N、S中所有成员都安全地接收到新的组密钥K。

例如：分布式多播组有n=4m个成员，先将其分成4个子组，每个子组包含4m-1个成员，再将子组继续以4个成员为一组进行划分，直到最后产生若干个小组，每

个小组都有4个成员；然后通过如下步骤生成组密钥。

1）第一组的4个成员M1、M2、M3和M4计算出所在球的球心O1，然后计算出半径R1。

2）第二组M5、M6、M7和M8计算出所在球的球心O2，然后计算出半径R2。

3）以此类推，直到最后一组计算出它们所在球的球心On和半径Rn。

4）将1）和2）中得到的球心O1、O2、…、On按4个一组再次进行划分，然后重复1）和2），直到得到根球心O和根半径R。这个根半径就是分布式多播的组密钥，如图1所示。

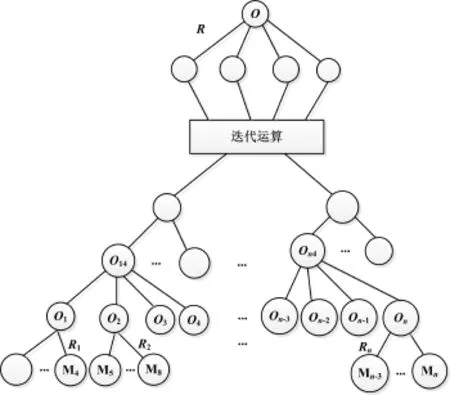
图1 n个成员协商组密钥

1.2 组成员的加入和离开

当有成员加入或离开多播组时，为了保证分布式多播的安全性，组密钥必须进行更新。本文考虑具有16个成员的分布式多播组的组密钥更新。

（1）假设M4请求加入多播组，由用户M1所在的子组接纳，如图2所示，那么从M1所在球的球心到根球心之间的所有相关的球心和半径都会发生变化。组密钥更新的具体步骤如下：

1）M1与M2、M3、M4计算出新的球心和半径，这个新的半径成为该组新的子组密钥，记为；

2）M1与M5、M9、M13根据各组的球心计算出新的父球心和半径，这个新的半径即为新的组密钥，记为；

以下表达式说明了组密钥的更新过程，如第1行是指以M1用加密发送给｛M2，M3，M4｝。

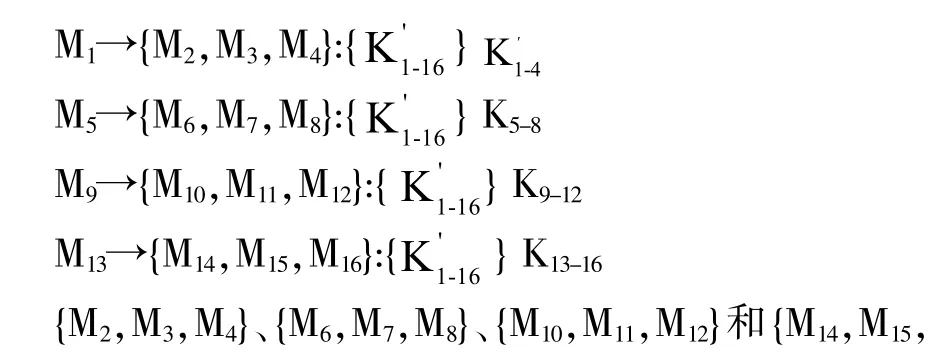
M16｝收到更新报文后，用各自所在子组的子组密钥解密即可得到。

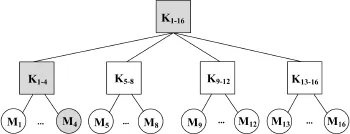
图2 成员M4加入时需要更新的密钥

（2）假设M1离开多播组，为了保证后向安全性，M1知道的密钥都需要更新，如图3所示。

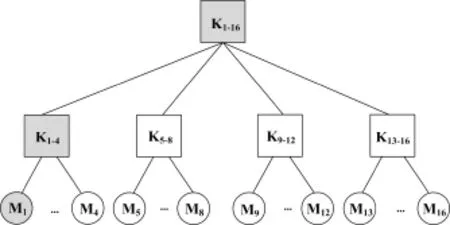
图3 成员离开时需要更新的密钥

密钥更新的步骤如下：

1）M2取代M1成为M3和M4的发起人；

2）M2与M3、M4共同决定一个球，计算出该球的球心和半径，这个半径即为新的子组密钥；

3）M2与M5、M9、M13根据各组的球心重新计算父球心和半径，以新的半径作为新的组密钥，记为；

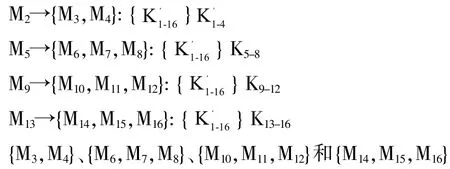
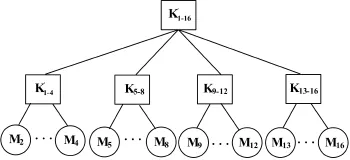
图4 成员M1离开后的超球结构

2 性能分析

2.1 安全性分析

在本方案中，当有成员加入多播组时，必然会引起从该成员所在的叶子节点到超球的根球心这条路径上的所有节点的坐标的变化，那么这条路径上的所有相关球的半径也会发生变化，即这条路径上所有的密钥全部更新。新的组密钥由每组的发起成员用子组密钥加密后，安全地传递给多播组中的其他成员，使新加入的组成员无法获取原来的组密钥，也就无法破解在其加入之前的多播消息，保证了多播的后向安全性。

同样，当有成员离开多播组时，从该成员所在的子组到超球的根球心这条路径上的所有节点的坐标也都会发生变化，即将产生新的子组密钥和多播组密钥。每组的发起成员将组密钥安全地发送给多播组内的剩余成员，而离开的成员是无法计算出新的子组密钥和新的组密钥的，即保证了多播的前向安全性。

2.2 复杂度分析

从以上分析可以看出，在n个成员组成的超球模型分布式多播中，只需要进行log4n轮迭代运算就可以产生组密钥。

从密钥存储的角度来分析，每一组中除了发起成员以外，其他成员只参与了该子组的密钥协商运算，剩下的迭代运算都只是由每一组的发起成员来完成，组密钥产生以后，也由发起成员负责将其转发给各组的其他成员。因此，在基于超球模型的分布式多播中，每个成员只需要保存两个密钥即可。

当有成员加入时，新加入的成员所在的子组需重新计算子组密钥，并和其他的子组进行log4n轮迭代运算来产生新的组密钥。新的组密钥由各组的发起成员加密后发送给各组的成员，共需要进行log4n次加密运算，故计算量为O（log4n）。由于每一组中除发起成员以外，都需要通过发送更新报文进行密钥更新，对每组4个成员的多播组来说，通信开销为3log4n。

成员离开时情形与成员加入时相同，发起成员需要进行log4n轮迭代运算产生新的组密钥，之后进行log4n次加密运算后发送给其他多播成员，通信开销为3log4n。

综上所述，在多播组成员数为n的情况下，密钥存储的复杂度为O（1），计算量和通信量为O（log4n），该方案具有良好的可缩放性。

3 结束语

基于超球模型的分布式密钥管理方案是将超球模型引入到了分布式多播中，该方案具有良好的扩展性和安全性，这种密钥组织方式可以有效降低密钥更新时的开销，提高分布式多播密钥更新的效率。

［1］STEINER M，WAIDNER M，TSUDIK G.CLIQUES：A New Approach to Group Key Agreement［C］//Proceedings of the The 18thInternational Conference on Distributed Computing Systems，IEEE Computer Society，Baltimore，Maryland，May 10-13，1997，IEEE，1998：380.

［2］DIFFIEW，HELLMANME.NewDirectionsin Cryptography［J］.IEEE Trans onInformation Theory，1976，22（6）：644-654.

［3］KIM Y，PERRIG A，TSUDIK G.Tree-based Group Key Agreement［J］.ACM TransInf Syst Secur，2004，7（1）：60-96.

［4］陈少军，冯年荣，许勇，等.基于超球形的多播密钥更新方法［J］.安徽工程科技学院学报（自然科学版），2007（3）：48-50.

［5］谢海涛，王玉明，杨宗凯，等.一种M维几何球形组播密钥批量更新方案［J］.小型微型计算机系统，2010（2）：254-258.

【责任编辑 梅欣丽】

Research on Distributed Multicast Rekeying Schema Based on Super Geometry Sphere

YANG Fan
（Department of ElectronicInformation and Engineering，Anhui Business College，Wuhu 241002，China）

A distributed multicast rekeying schema based on super geometry sphere was proposed.The schema took full advantage of both independent and collaborative features among members of distributed multicast to solve the security problem of multicast rekeying；in the same time，the higher efficiency updating of the program effectively reduced communication overhead of the group rekeying without increasing the computational and storage overhead and it could ensure the forward and backward security while updating.

distributed multicast；multicast security；rekeying；super geometry sphere

TP393

A

2095-7726（2015）12-0040-04

2015-07-01

杨帆（1989-），男，安徽怀宁人，助教，硕士，研究方向：网络安全与移动互联。