基于超混沌模型的彩色图像自相关加密算法

徐 洁

（山西金融职业学院计算机系，山西　太原　030008）

基于超混沌模型的彩色图像自相关加密算法

徐 洁

（山西金融职业学院计算机系，山西太原030008）

随着计算机网络的发展和普及，多媒体安全越来越受人们的重视.在这种背景下提出了一种建立在超混沌模型下的自相关图像加密算法.该算法的模型基础为chen混沌的一个变种，这大大扩展了加密算法的秘钥空间，在加密中使用图像自相关加密方式，使得加密算法可以有效的抵抗明文攻击.实验结果表明，该算法具有优良的性能.关键词：超混沌模型；图像加密；图像自相关

近年来，随着网络增速越来越快，图像、视频等多媒体信息越来越成为计算机网络中最为广泛使用的信息载体之一.图像由于其大小适宜、载体信息丰富等特点，更是频繁的被人们作为传递消息的载体.然而，传统的加密算法被认为并不适合进行图像加密，因为传统的MD5或者SHA等散列函数的输出为一维的随机数序列，而图像加密需要与图像大小相同的密钥序列.国内外学者纷纷将目光投向如何根据图像本身的特点来设计图像加密算法上.

混沌系统由于其拥有对初值的敏感性、遍历性好、不可预测性等优点，已经被广泛引用于图像加密.1989年，Matthews［1］提出了一种基于混沌的图像加密算法.然而由于低维的混沌系统存在动态特性简单、只有较少的初值参数、加密代码简单等缺点，科学家们渐渐将目光投向基于高维混沌系统的图像加密算法.由于超混沌系统有多个正的Lyapunov指数，它的动态行为更难被攻击者预测，因此应用它的加密算法可以拥有的更高安全性能.

彩色图像携带有比灰度图像更加丰富的信息，因而成为图像中最为广泛使用的对象［2］，彩色图像越来越受学术界重视［3-7］.本文提出一种基于超混沌系统的彩色图像自相关加密算法，并对它进行了性能分析，实验证明它可以有效的抵抗明文攻击等攻击.

1　超混沌系统

本文所采用的超混沌系统为Chen′s模型［8］的一个变种，它的模型具体描述如下：其中：a，b，c，d为参数，当a=36，b=3，c=28，d=-16，-0.7≤k≤0.7时，该系统表现为超混沌状态.选取a=36，b=3，c=28，d=-16，k=0.2时，超混沌系统的吸引子如图1所示.它的Lyapunov指数分别是λ1=1.552，λ2= 0.023，λ3=0，λ4=-12.573.由于该超混沌系统具有两个正的Lyapunov指数，所以它的预测时间要比混沌系统［9］具有更短的预测时间，这证明它在加密算法中具有更高的安全性能.

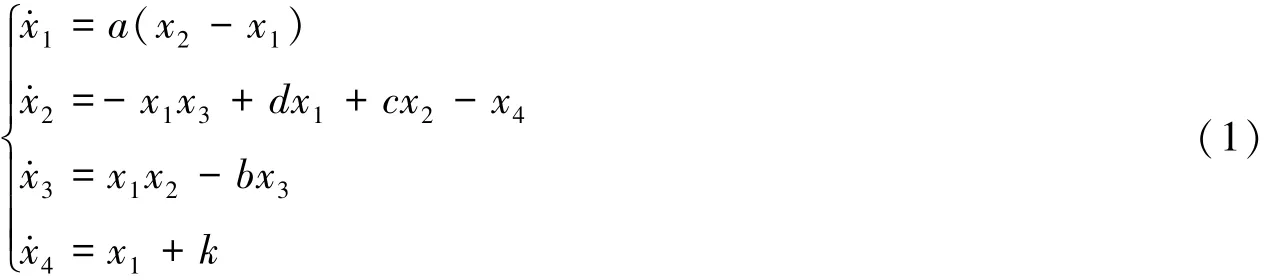
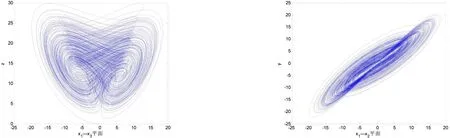
图1　超混沌系统（1）的吸引子图Fig.1 Hyper-chaos attractors of system（1）

2　彩色图像加密算法

证明上述的超混沌系统具有随机性、非周期性、初值敏感性等混沌特性，所以它可以作为一个性能良好的伪随机数发生器.在自然界，色彩随处可见，图像的彩色信息也是图像的重要信息之一，彩色图像加密也越来越受学术界重视.我们在此基础和背景下提出一个彩色图像自相关加密算法.

彩色图像是图像中每个像素由R、G、B分量构成的图像，其中R、G、B由不同的灰度级来描述，三基色模型是建立图像成像、显示的基础，就有十分重要的作用，如图2所示.

在本文中首先将图像分解成RGB三个通道，如式（2）所示；然后分别对三个通道分别加密；解密时将各个通道组合起来来完成加密方案.

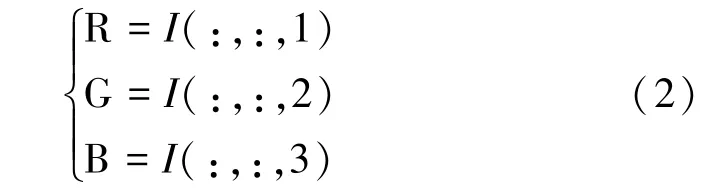
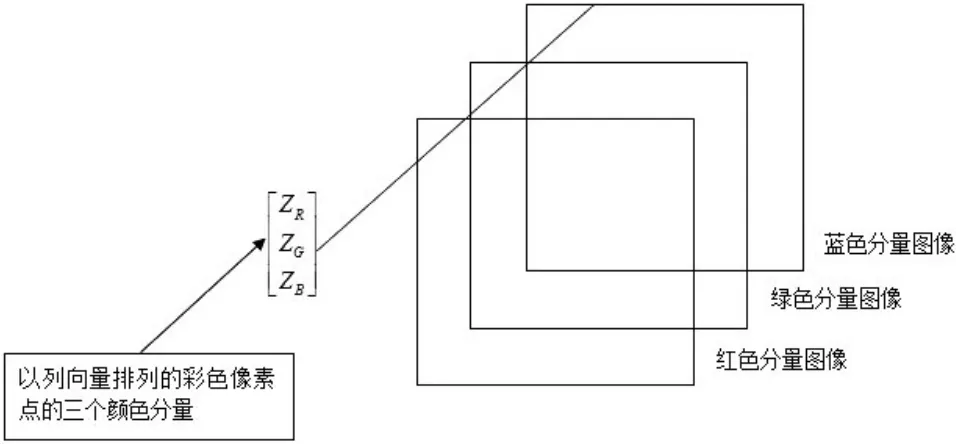
图2　彩色图像的表示Fig.2 The representation of a color image

假设原始图像的大小为M×N，则加密算法描述如下：

1）首先读入原始图像，并按式（2）将其分解为RGB三通道分量，如图2所示.

2）针对每个分量，将分解为4等份，以R通道为例，将这4等份标记为R1、R2、R3、R4.以彩色图像Baboon为例，按图3所示.

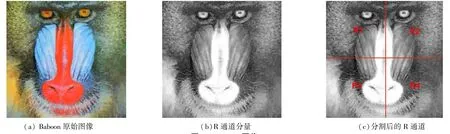
图3　Baboon图像Fig.3 Baboon image

3）根据R1、R2、R3、R4的所有像素灰度值总和的大小确定这4等份的加密顺序，针对该图像，它的加密顺序为R1→R2→R3→R4.

4）除R1外，自己初始值作为加密秘钥，其他图像块，以R2为例，将加密的图像块R2前一等份图像R1的加密图像的前4位灰度值作为超混沌系统（1）的初始值输入，产生混沌序列p.并将序列值转化为0～255的整数，如式（3）所示.

式中，mod为模操作，floor为向下去整操作.最后将图像块与变换后的序列进行异或操作，如式（4）所示.

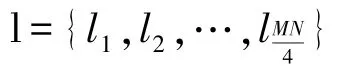
6）至此，完成了图像块R1的第一轮加密，按照同样的方式对其它图像进行加密.

7）重复步骤（4）～（6）完成R最终加密.

通过相同的步骤，可以完成G通道分量和B通道分量的加密.图像的解密为图像加密的逆反操作.

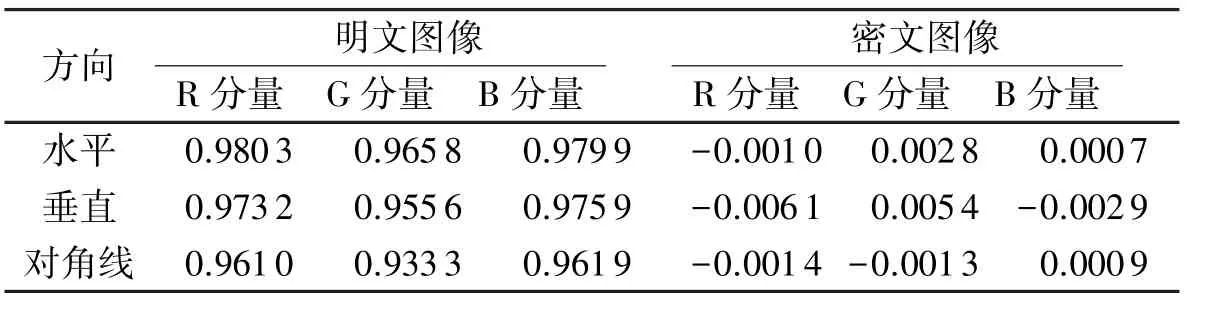
表1　明文图像和加密图像的相关系数对比Tab.1 Comparison of correlation coefficients of the plain-image and the cipher-image

3　数字仿真及分析

本文实验仿真所使用的平台为MATLAB R2013a，运行环境为Windows7，配置为Intel（R）Core（TM）i3-2370M CPU 2.40GHz 2GB RAM.本文所采用的图像为经典的测试图像Baboon，大小为360×360像素，如图4（a）所示.利用本文加密算法进行加密，加密结果如图4（b）所示，解密结果如图4（c）所示.

图4　Baboon加密仿真Fig.4 Baboonencryption

从图4可以发现，经过本文加密算法的加密之后，在视觉上无法从加密图像中得到有效信息，并且解密算法可以完全解密，复原原始信息.下面对图像加密算法的性能进行分析.

3.1直方图分析

直方图是检验图像加密算法安全性的一种重要手段，它可以有效反映加密算法针对灰度攻击的抵抗能力.在图5中列出了对Baboon在RGB三个通道的直方图分析.

从图5中可以看到，原图像的灰度值是集中在一起的，而加密后的图像的灰度值则是均匀而平滑的分布，这表明原始图像的统计特性已经被完全扩散到加密图像的平均分布中了，所以提出的算法具有良好的抗统计分析攻击的能力.

3.2相关性分析

一个理想的加密方案产生的加密图像的相邻像素之间的相关性应该足够的低.使用式（6）分别从水平、垂直、和对角线方向分别计算三个颜色分量的相关性，计算结果如表1所示.从表1中可以看出，加密图像的相关性非常低接近于0，这表明加密算法可以大大提高图像的安全性.图6反映了Baboon和其密文图像的R、G、B分量在对角线上的相关性.从图中可以看出Baboon明文图像的像素比较集中，具有很强的相关性，而密文图像中像素值分布比较均匀，相关性较低.这表明该算法有较高的对抗统计攻击的能力.

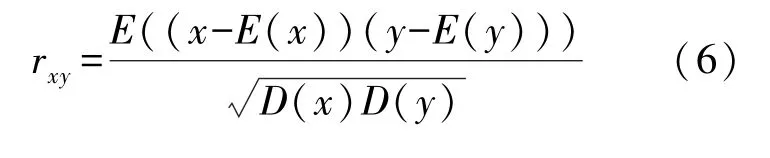
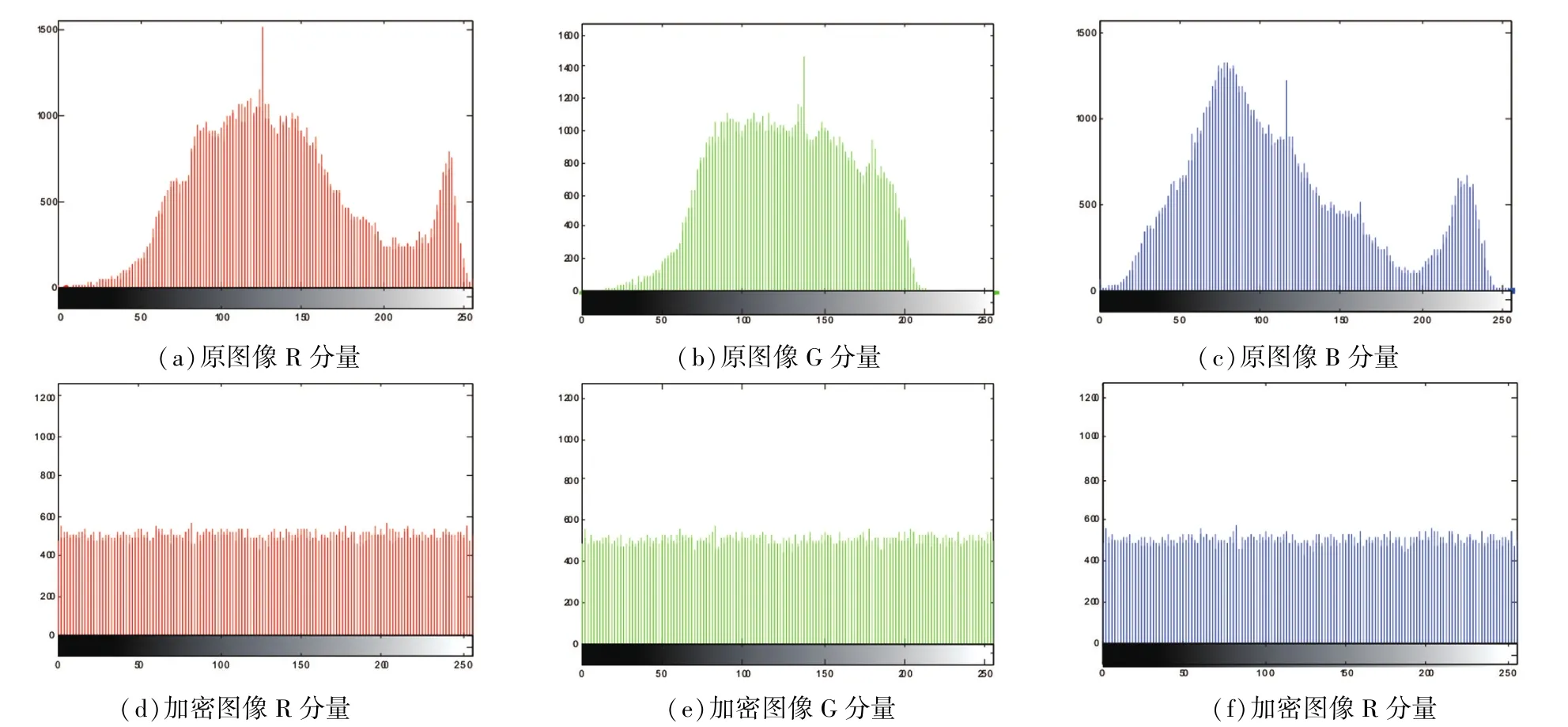
图5　原始明文图像与加密图像的直方图比较Fig.5 Comparison of Histograms of the plain-image and the cipher-image

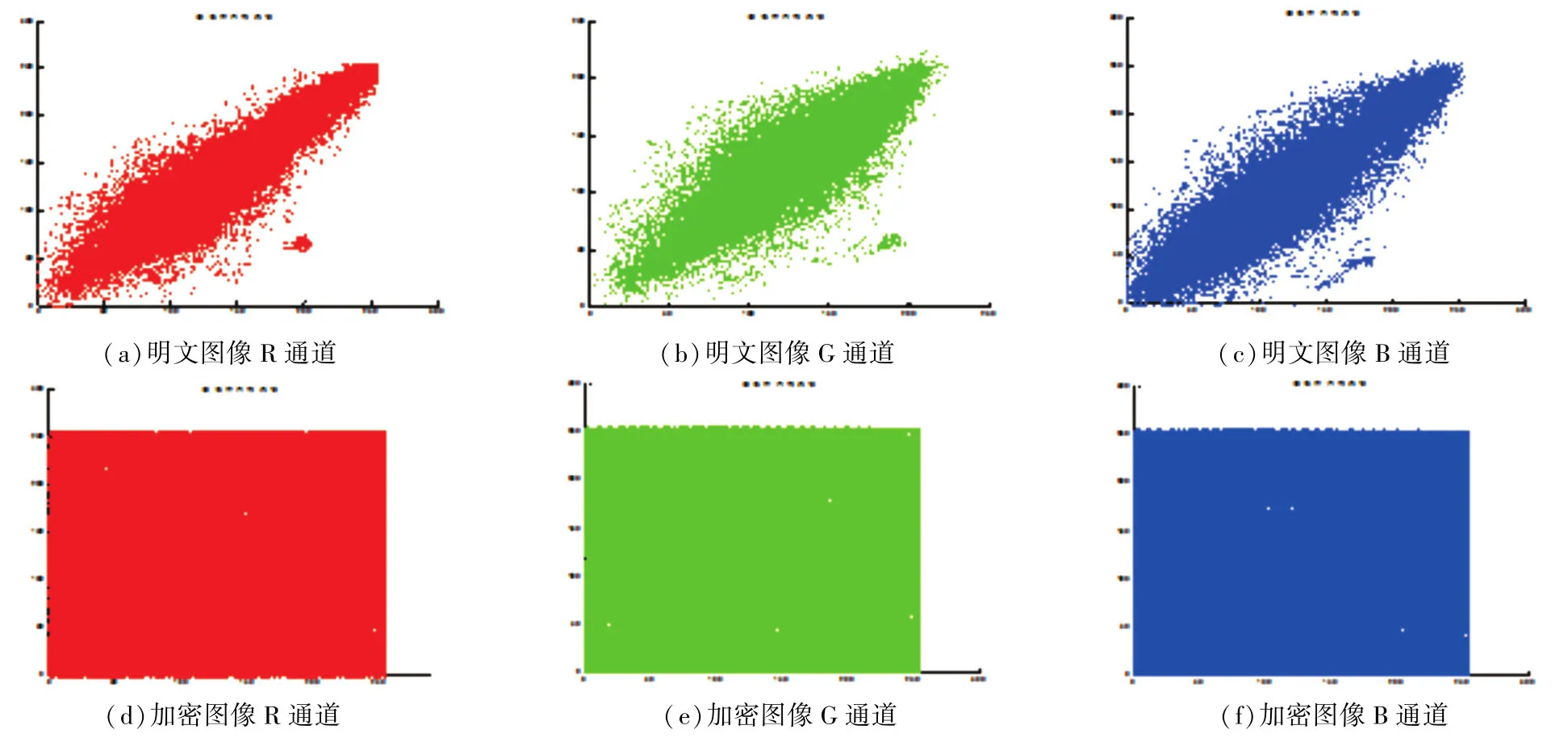
图6　原始图像和加密图像的在对角线上相邻像素相关性比较Fig.6 Correlation analyses.（a）R Channel of plain-image

3.3明文敏感性分析

在明文图像中的一个小小的变化可以引起密文图像的差异，这种变化反映了明文图像和密文图像的某种程度的关系，这常常被攻击者用来进行明文攻击.有效安全的加密算法应该对明文敏感，明文图像的任何微小变动都会使得加密和解密后得到的图像有很大的差异.在一般情况下，两种常见的性能测试工具被用来测量这种微小变化带来的影响，即像素变化率（NPCR）和统一平均变化强度（UACI）.

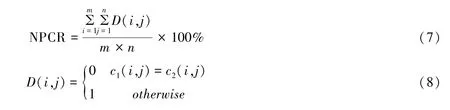
NPCR如式（7）和式（8）所示：其中：c1和c2分别表示明文图像经过微小变化前后经过加密算法加密而获得的加密图像，大小为m×n.UACI定义如式（9）所示：

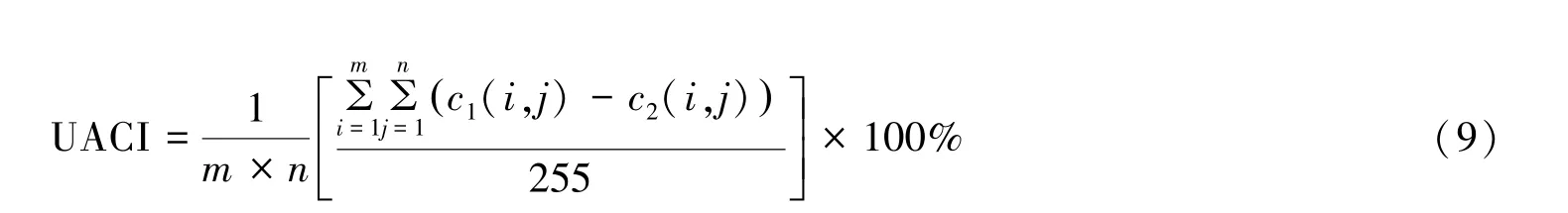
通过计算可以得到NPCR值为99.61%，UACI最终结果为33.4565%，这证明该算法可以对明文十分敏感，可以有效的抵抗明文攻击.

3.4秘钥敏感性分析

一个性能良好的加密算法，当使用不同的秘钥对同一个对象进行加密时，得到的结果也应该不同；并且使用不正确的秘钥无法正确解密加密图像.图7（a）为使用key=0.4得到的加密图像，图7（b）为使用key= 0.25得到的加密图像，经过计算可得它们的NPCR值为99.60%，这表明它们是完全不同的；图7（c）为使用key=0.25来解密key=0.4的加密图像得到的结果，可以看出无法得到正确的解密图像.以上分析表明加密算法对秘钥是敏感的.

图7　秘钥敏感性分析Fig.7 Key sensitivity tests

4　结语

随着计算机网络的发展和普及，多媒体安全越来越受人们的重视.本文针对传统的一维混沌系统的动态特性简单、只有较少的初值参数、加密代码简单等缺点，提出了一种建立在超混沌模型下的自相关图像加密算法.该算法在安全测试中表现良好，可以有效的抵抗明文攻击和统计攻击，相较于传统的混沌加密具有更加复杂的动态特性.

［1］R Matthews.On the derivation of a chaotic'encryption algorithm［J］.Cryptologia，1989，13（1）：29-42.

［2］余成波.数字图像处理及MATLAB实现［M］.重庆：重庆大学出版社，2003.

［3］LIU F，WU C K，LIN K J.Colour visual cryptography schemes［J］.IET Information Security，2008，2（4）：151-165.

［4］SHYU S J.Image encryption by multiple random grids［J］.Pattern Recognition，2009，42（7）：1582-1596.

［5］王英，郑德玲，王振龙.空域彩色图像混沌加密算法［J］.计算机辅助设计与图形学学报，2006，18（6）：876-880.

［6］RHOUMA R，MEHERZI S，Belghith S.OCML-based colour image encryption［J］.Chaos，Solitons&Fractals，2009，40（1）：309-318.

［7］HUANG C K，NIEN H H.Multi chaotic systems based pixel shuffle for image encryption［J］.Optics Communications，2009，282（11）：2123-2127.

［8］GAO T G，CHEN Z Q，YUAN Z Y，et al.A hyperchaos generated from Chen′s system［J］.Int J Mod Phys C，2006，17：471-478.

［9］YANCHUK S，KAPITANIAK T.Symmetry-increasing bifurcation as a predictor of a chaos-hyperchaos transition in coupled systems［J］.Phys Rev E，2001，64：056235.

责任编辑：时 凌

Color Image Encryption Algorithm Based on Hyper Chaos Model

XU Jie
（Department of Computer，Shanxi Professional College of Finance，Taiyuan 030008，China）

With the development and popularization of computer network，the security of multimedia is becoming more and more important.In this paper，a self-related image encryption algorithm based on hyper chaos model is proposed.The algorithm of the model is a mutation of Chen′s chaotic，which greatly expanded the key space of the encryption algorithm.When using use image autocorrelation encryption，the encryption algorithm can effectively resisting plaintext attacks.Experimental results show that this algorithm has good performance.

hyper chaos model；image encryption；image auto correlation

TP309

A

1008-8423（2015）04-0412-05DOI：10.13501/j.cnki.42-1569/n.2015.12.015

2015-11-16.

徐洁（1987-），女，硕士，主要从事图像处理、智能信息处理的研究.