微结构固体中的非光滑孤立波

张 芳，那仁满都拉

（1.内蒙古民族大学数学学院，内蒙古　通辽　028043；

2.内蒙古民族大学物理与电子信息学院，内蒙　古通辽　028043）

微结构固体中的非光滑孤立波

张 芳1，那仁满都拉2*

（1.内蒙古民族大学数学学院，内蒙古通辽028043；

2.内蒙古民族大学物理与电子信息学院，内蒙古通辽028043）

完善微结构固体的自由能形式，使其包含宏观形变和微形变的全部二次项及宏观形变的三次项，并根据Engelbrecht等修正的微结构弹性理论，严格推导出了描述微结构固体中一维纵波传播的一种新模型.对所得模型进行研究，得到了该模型方程的尖峰孤立波解，进而证明了在一定条件下微结构固体中也可以存在尖峰孤立波.这一结论进一步推广了微结构固体中只存在光滑孤立波的已有结论.

微结构固体；非光滑孤立波；非线性波模型

微晶、合金、陶瓷及岩石等材料，由于它们内部结构上存在孔隙、位错、颗粒、裂纹及裂缝等微结构，当观测尺度接近微结构尺寸时，可表现出与经典材料极为不同的行为特征.如高频弹性波的弥散现象以及在裂纹尖端处出现的无限大应力现象等，这些现象用经典连续介质理论无法得到满意的解释.为此，Mindline和Eringen等提出了考虑微结构的弹性固体理论［1-4］.Engelbrecht等对微结构弹性理论进行了完善和修正，并开始研究了微结构固体中孤立波的形成条件与传播规律［5-9］.了解微结构固体中孤立波的形成条件与传播规律，可对固体材料的检测与评价提供重要的理论基础.文献［10］中已证明了运用微结构固体中形成的孤立波所携带的信息可以准确地判定材料的微结构参数［10］.文献［11-14］中给出了微结构固体中可以存在对称和非对称钟型孤立波等光滑孤立波的结论，并没有给出微结构固体中可以存在尖峰孤立波等非光滑孤立波的结论.

本文通过完善微结构固体的自由能形式，使其包含宏观形变和微形变的全部二次项及宏观形变的三次项，将建立微结构固体中纵波传播的一种新模型，进而分析微结构固体中可能存在的尖峰孤立波.

1　建立模型

微结构固体中纵波传播的一维运动方程为［11-12］：

其中：u表示宏观位移，σ表示宏观应力，ψ表示微形变，η表示相应的微应力，τ表示微元体间的相互作用力，ρ和I是宏观密度和微惯性.在文献［9-14］中采用的自由能形式都是比较特殊的情况，即考虑宏观形变和微形变的特殊几个二次项的基础上就考虑了宏观形变和微形变的三次项或四次项.按照微结构弹性固体理论，一般只有考虑全部二次项的基础上，才可以考虑三次项或四次项等高次项.针对这一问题，本文在自由能的表达式中考虑全部二次项的基础上考虑了宏观形变的三次项，忽略了微形变的三次项.因为实际的微结构固体材料的微尺度非线性效应远比宏观尺度非线性效应要弱，所以本文采用的自由能形式为：

波方程时，文献［11-14］中都利用了从属原理，所以得到的波方程都是近似的.本文经过精确地推导，得到了微结构固体中一维纵波传播的非线性波方程.

2　尖峰孤立波

利用文献［15-16］中给出的待定系数法，求解方程（12）得到了以下尖峰孤立波解.

2.1尖峰孤立波解

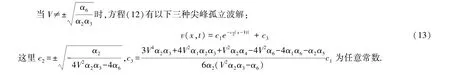
非线性波方程（12）有尖峰孤立波解（13）～（15），这表明微结构固体中可以存在尖峰孤立波.

3　结论

本文首先完善微结构固体的自由能形式，使其包含宏观形变和微形变的全部二次项以及宏观形变的三次项，然后根据Engelbrecht等修正的微结构弹性固体理论，严格导出了描述微结构固体中一维纵波传播的一种新模型.对所得新模型进行研究，得到了该模型方程的尖峰孤立波解，进而证明了在一定条件下微结构固体中也可以存在尖峰孤立波等非光滑孤立波.这一结论进一步推广了微结构固体中只存在光滑孤立波的已有结论，这些结论对固体材料的无损检测及其性能的评价提供了重要理论基础.

［1］虞吉林.考虑微结构的固体力学的进展和若干应用［J］.力学进展，1985，15（1）：82-89.

［2］MINDLIN R D.Micro-structure in linear elasticity［J］.Archive for Rational Mechanics and Analysis，1964，16（1）：51-78.

［3］程昌钧.理性力学在中国的传播与发展［J］.力学与实践，2008，30（1）：10-17.

［4］GIRIBET M C，RIBAS A I.Kinetics of colour development in aqueous fructose systems at high temperatures［J］.Journal of the Science of Food and Agriculture，2000，80（14）：2105-2113.

［5］PORUBOV A V，PASTRONE F.Nonlinear bell-shaped and kink-shaped strain waves in microstructured solids［J］.International Journal of Non-Linear Mechanics，2004，39（8）：1289-1299.

［6］PORUBOV A V，AERO E L，Maugin G A.Two approaches to study essentially nonlinear and dispersive properties of the internal structure of materials［J］.Physical Review E，2009，79，046608：1-12.

［7］RANDRUUT M，BRAUN M.On one-dimensional solitary waves in microstructured solids［J］.Wave Motion，2010，47（4）：217-230.

［8］BEREZOVSKI A，ENGELBRECHT J，Berezovski M.Waves in microstructured solids：A unified viewpoint of modeling［J］.Acta Mechanica，2011，220（4）：349-363.

［9］SALUPERE A，TAMMK.On the influence of material properties on the wave propagation in Mindlin-type microstructured solids［J］.Wave Motion，2013，50（7）：1127-1139.

［10］JANNO J，ENGELBRECHT J.An inverse solitary wave problem related to microstructured materials［J］.Inverse Problems，2005，21（6）：2019-2034.

［11］JANNO J，ENGELBRECHT J.Solitary waves in nonlinear microstructured materials［J］.Journal of physics A：Mathematical and General，2005，38（23）：5159-5172.

［12］ENGELBRECHT J，PASTRONE F.Wave in microstructured solids with nonlinearities in microscale［J］.Proceedings of the Estonian Academy of Sciences，Physics，Mathematics，2003，52（1）：12-20.

［13］那仁满都拉，额尔敦仓.立方非线性微结构固体中的对称孤立波及存在条件［J］.应用数学和力学，2014，35（11）：1210-1217.

［14］那仁满都拉.微结构固体中的孤立波及其存在条件［J］.物理学报，2014，63（19）：194301.

［15］钱素平，田立新.广义强色散DGH方程的新型孤立波解［J］.江苏大学学报（自然科学版），2006，27（3）：279-282.

［16］刘煜.非线性波方程尖峰孤子解的一种简便求法及其应用［J］.物理学报，2009，58（11）：7452-7457.

责任编辑：时 凌

Non-smooth Solitary Waves in Microstructured Solids

ZHANG Fang1，Naranmandula2*
（1.College of Mathematics，Inner Mongolia University for the Nationalities，Tongliao 028043，China；
2.College of Physics and Electronic Information，Inner Mongolia University for the Nationalities，Tongliao 028043，China）

The improvement of the free energy form for microstructured solids was made，which contains all quadratic terms of macro-and microdeformation and cubic term of macrodeformation.According to the microstructured elastic theory modified by Engelbrecht and others，a new model capable of describing the longitudinal wave propagation in one-dimensional microstructured solids was strictly derived.The acquired model was studied and the peakon solutions were obtained.And thus，the existence of the peakon in microstructured solids was proved under certain conditions.This conclusion further extends the conclusion that only the smooth solitary wave can be found in microstructured solids.

microstructured solid；non-smooth solitary wave；nonlinear wave model

O331；O347

A

1008-8423（2015）04-0369-03DOI：10.13501/j.cnki.42-1569/n.2015.12.003

2015-11-23.

国家自然科学基金项目（11462019）；内蒙古民族大学研究生科研创新资助项目（NMDSS1420）.

张芳（1991-），女（蒙古族），硕士生，主要从事数学机械化及其应用；*

那仁满都（1963-），男（蒙古族），博士，教授，主要从事非线性物理的研究.