泰国湾及邻近海域潮汐潮流的数值模拟
吴頔,方国洪,2*,崔欣梅,2,滕飞,2
(1.国家海洋局第一海洋研究所,山东青岛266061;2.海洋环境科学和数值模拟国家海洋局重点实验室,山东青岛266061)
泰国湾及邻近海域潮汐潮流的数值模拟
吴頔1,方国洪1,2*,崔欣梅1,2,滕飞1,2
(1.国家海洋局第一海洋研究所,山东青岛266061;2.海洋环境科学和数值模拟国家海洋局重点实验室,山东青岛266061)
本文基于FVCOM(Finite-Volu me Coastal Ocean Model)模式,模拟了泰国湾及其周边海域K1、O1、M2和S2四个主要分潮。采用47个验潮站实测调和常数与模拟结果进行比较,所得4个分潮的均方差分别为4.06 cm、3.76 cm、8.22 cm和4.71 cm,符合良好。根据计算结果分析了泰国湾及其周边海域的潮汐、潮流的分布特征和潮波的传播特征。数值试验表明,现有的数字水深资料(ETOPO1,ETOPO5,DBDB-V)的准确度不足以合理地模拟泰国湾潮波。
FVCOM;潮汐;潮流;泰国湾;数值模拟
吴頔,方国洪,崔欣梅,等.泰国湾及邻近海域潮汐潮流的数值模拟[J].海洋学报,2015,37(1):11—20,doi.10.3969/j.issn.0253-4193.2015.01.002
Wu Di,Fang Guohong,Cui Xinmei,et al.Numerical simulation of tides and tidal currents in the Gulf of Thai land and its adjacent area[J].Haiyang Xuebao,2015,37(1):11—20,doi.10.3969/j.issn.0235-4193.2015.01.002
1 引言
泰国湾,旧称暹罗湾(Gulf of Siam),位于南海西南部的巽他陆架之上,处于太平洋及其附属海的最西端,是南海最大的一个海湾。泰国湾及其周边海域大部分地区水深在50 m左右(见图1),由于该海域处于低纬度地区,科氏加速度较小,其半日潮波系统相对复杂。以M2分潮为例,其于泰国湾湾口存在一个顺指针旋转的无潮点,这有悖于北半球无潮点呈逆时针旋转的一般规律,因此一直受到众多学者的关注,而其在泰国湾湾顶无潮点的存在性及位置,直至今日各学者给出的结果仍不尽相同。
早在1944年,Dietrich[1]就绘出了南海(含泰国湾)的同潮图,但他给出的同潮图基本上不能反映南海潮波的主要结构。而Defant[2]、Ye和Robinson[3]、俞慕耕[4]绘制的同潮图,虽结果有所改善,但相互之间的差异十分显著。此后,丁文兰[5]、Fang[6]、Yanagi和Toshiyuki[7]、Fang等[8]、Cai等[9],Zu等[10],吴頔[11]也给出了包括泰国湾的同潮图。其中对于M2分潮在泰国湾湾口无潮点的认识基本一致,但湾顶无潮点是否存在及确切位置依旧存有争议。此外,毛庆文等[12]对沿轨高度计的分析显示S2分潮在大纳土纳岛附近不存在无潮点,这与Fang等[8]的模拟结果不相同。
由此可见,泰国湾是众多学者研究结果存在差异最大的海域而目前单独对泰国湾进行的研究相对较少。本文利用FVCOM[13]海洋数值模式,建立了泰国湾及周边海域的二维潮汐数值模型,同时对K1、O1、M2和S2四个主要分潮进行模拟,利用验潮站数据对模拟结果进行验证,最后分析了泰国湾其周边海域的潮汐、潮流的分布特征和潮波的传播特征。

图1 研究海域及水深分布图Fig.1 Study area and its bathymetry
2 数值模式和计算过程
2.1模式介绍
本文采用的数值模式为由马萨诸塞大学海洋科技研究院和伍兹霍尔海洋研究所联合开发的无结构有限体积海洋数值模式FVCOM(Finite-Volu me Coastal Ocean Model)。该模式的原始方程包括动量方程、质量连续方程以及温度、盐度和密度方程,并在垂向采用σ坐标拟合不规则的海底地形。它的三角形无结构网格可以更好模拟复杂岸形的实际海洋。本文旨在模拟研究海域的正压潮,因此采用二维模式。
2.2计算区域及网格设置
本模型模拟区域范围为0°~14°N,98°~118°E,包括泰国湾、巽他陆架西北部海域。利用SMS软件生成三角网格系统,对岸边和岛屿的网格进行了局部加密,开边界平均分辨率约(1/3)°,岸线及岛屿附近平均分辨率约(1/20)°,共包含8 622个网格节点,15 964个三角单元。
模式基于三角形网格的有限体积法,将连续方程和动量方程在三角形单元内积分后,通过改进的四阶龙格库塔方法求解。时间步长为6 s,计算的初始条件假设海洋是静止的,海表面的扰动水位初始值全部为0,所有三角形网格中心点的初始流速u=v=0。本文采用正压模式,取整个海域内的温度和盐度均为常数,温度为27℃,盐度为35。开边界上每个点的水位给定,由T_tide的预报程序给出(Pawlowicz等[14]),其中M2、S2、K1和O1调和常数来自DTU10(Cheng和Anderson[15])数据。底摩擦系数取0.001,模式运行30 d,对后15 d时间序列进行调和分析,得到网格点上的水位的调和常数、每个三角形中心点的潮流椭圆要素以及速度各分量的调和常数。
2.3水深资料的选取
目前对全球海洋有多种数字化水深资料。我们曾采用美国国家海洋大气局(National Geophysical Data Center,NOAA)发布的1′和5′分辨率的水深资料ETOPO1和ETOPO5,以及美国海军发布的变分辨率(1′,2′,5′)全球水深数据DBDB-V,分别对研究海域的潮汐进行模拟。研究发现,采用ETOPO1的模拟结果与实测数据符合程度最差,基本上不能模拟出各分潮的潮波结构;采用ETOPO5模拟所得的潮波结构基本尚可,但所得泰国湾北部M2分潮的无潮点偏离湾顶太远;采用DBDB-V的模拟结果略好,但泰国湾北部M2分潮的无潮点离湾顶仍较远,且离岸太远。用上述水深资料模拟所得同潮图及结果与实测值的偏差比较详见本文附图A1和表A1。由于采用DBDB-V水深数据的模拟结果相对较好,因此对我国海军航海保证部出版的泰国湾海图水深进行了数字化,并对DBDB-V水深数据加以修正,用于数值模拟。结果表明,采用海图水深大大改善了模拟结果,潮波结构与观测数据更为吻合。
3 模式结果验证
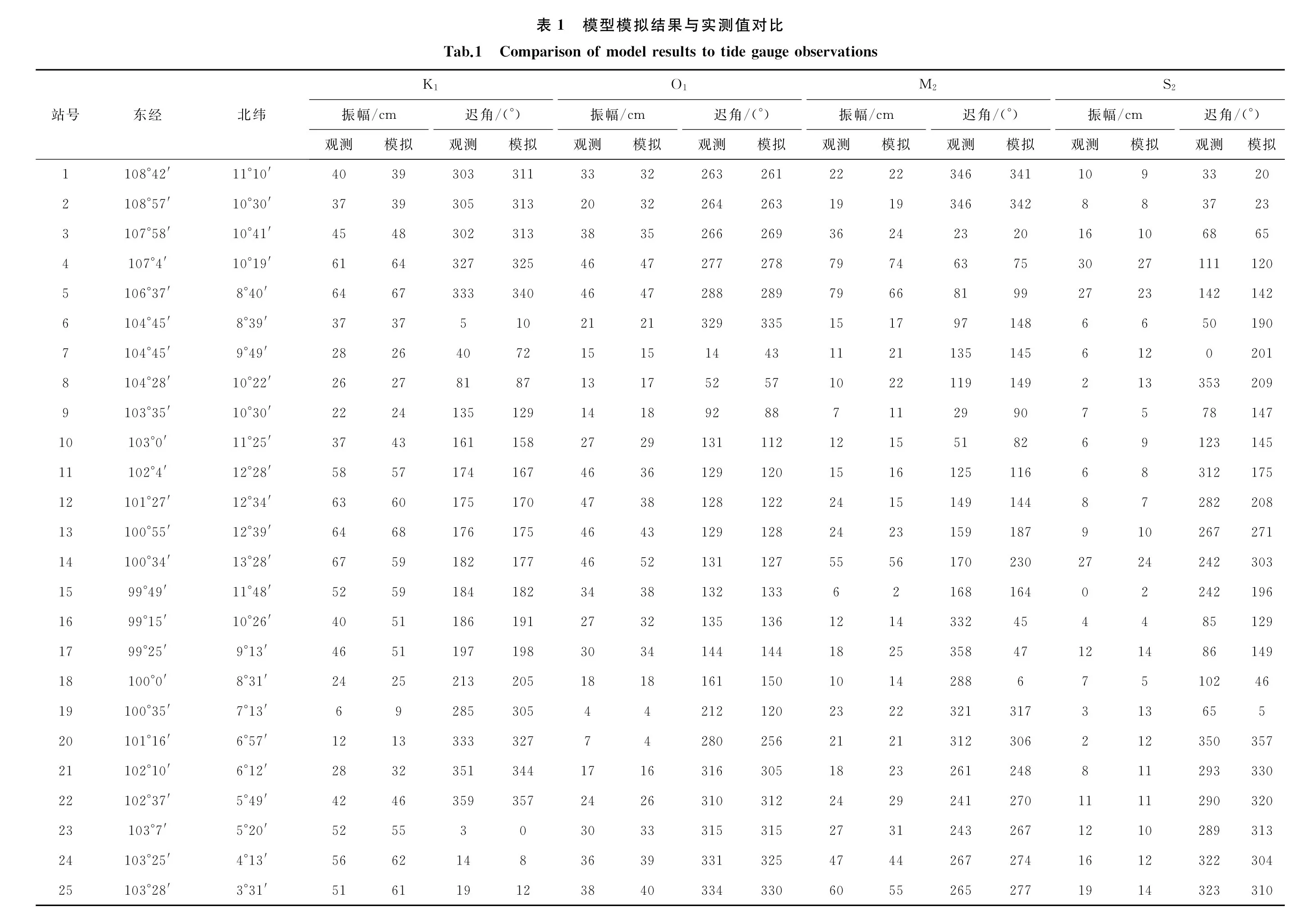
为了验证数值模拟结果,本文将模拟结果与验潮站数据进行了比较。挑选计算区域内及沿岸共47个验潮站的调和常数,站位分布如图2所示。所选验潮站覆盖文献[8]在计算区域内的所有28个验潮站(实心圆表示),又从国际水文组织(International Hydrographic Organization,IHO)潮汐调和常数数据集中选取共19个验潮站(空心圆表示)。模拟值与观测值之间的偏差采用下式计算:

式中,ε为模拟值和观测值在一个潮周期内的均方差;H和g为各分潮调和常数的振幅和迟角;下标s和o分别代表模拟结果和观测结果;k为验潮站的个数。这里ε同时考虑了分潮振幅和位相,对数值模拟效果的评估更加合理[16]。
表2中分别列出图2中验潮站的模拟结果与观测值,并计算给出ε。其中K1、O1、M2和S2偏差的平均值分别为4.06 cm、3.76 cm、8.22 cm和4.71 cm。因此,认为该模式模拟的结果是可信的。
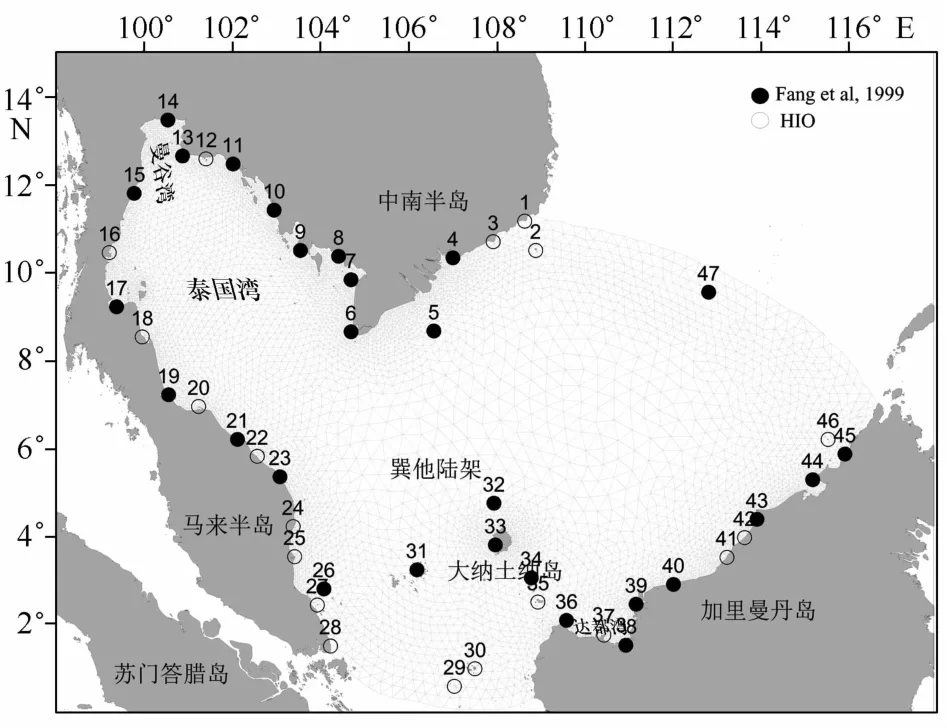
图2 计算网格及验潮站分布Fig.2 Computational grids and location of tide gauge stations
4 结果分析
4.1潮汐分布
图3~6分别给出了K1、O1、M2和S2四个主要分潮的同潮图(虚线为等振幅线,单位为m,实线为等迟角线,时间采用东8时区),其结构与Fang等[8]的模拟结果基本一致。其中两个全日潮波(K1和O1)结构相似,两个半日潮波(M2和S2)结构也相似,而全日潮和半日潮之间则差别很大[17]。
全日潮由于波长较长,因此潮波结构相对简单。K1分潮在曼谷湾及湄公河附近振幅逐渐增大,最大振幅超过60 cm。由于北半球科氏加速度作用,K1分潮在泰国湾内入射波东岸强西岸弱,反射波东岸弱西岸强,叠加形成一个逆时针旋转的潮波系统[17],由于摩擦耗散作用,无潮点靠近西岸。O1分潮的潮汐结构和K1基本一致,振幅较K1分潮略小,最大振幅达到40 cm左右。
半日潮的波长仅为全日潮的一半,故潮波的结构更为复杂。在泰国湾内M2分潮的振幅较小,大都在20 cm以下,湄公河口海域以及达都湾M2分潮的振幅向陆地方向逐步增大。在泰国湾湾顶M2分潮存在一个向北岸退化的无潮点,而M2分潮因泰国湾口的无潮点呈顺时针旋转,这有悖于北半球逆时针旋转的一般规律。这是由于M2分潮频率高,在低纬度区惯性频率比潮波频率小很多,因此在泰国湾中Kelvin波的性质较弱,湾口和湾顶主要受Poincaré波控制[18],而湾口迟角自东北向西南增加的梯度条件,即潮波传入方向,促使M2分潮在泰国湾湾口形成顺时针旋转的无潮点。本文模拟显示湾顶处的M2无潮点为一退化的无潮点,这与方国洪等[17]和Zu等[10]给出的结果一致,与Fang等[8]的结果有所不同。

图3 K1分潮同潮图Fig.3 Predicted cotidal chart for K1
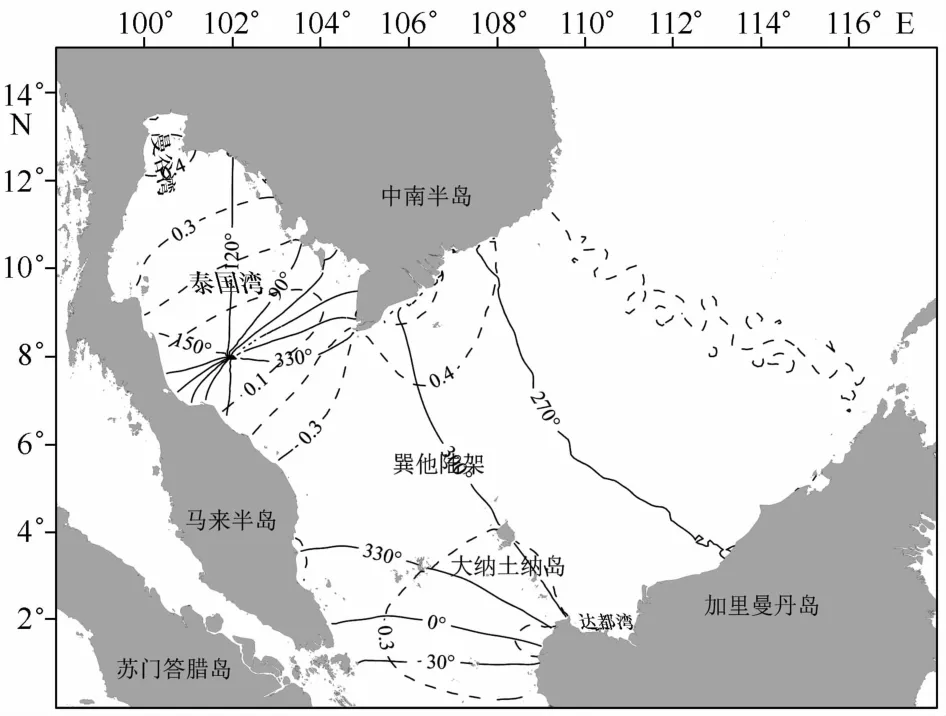
图4 O1分潮同潮图Fig.4 Predicted cotidal chart for O1
S2分潮分布与M2分潮大体一致,但振幅较M2分潮小,最大值出现在达都湾,大约40 cm。与M2分潮类似,S2分潮在泰国湾湾口均出现顺时针旋转的无潮点,而大纳土纳群岛西北部没有出现无潮点,此结果比Fang等[8]的结果更符合实际,与毛庆文等[12]利用高度计资料分析所得的结果一致。

图5 M2分潮同潮图Fig.5 Predicted cotidal chart for M2
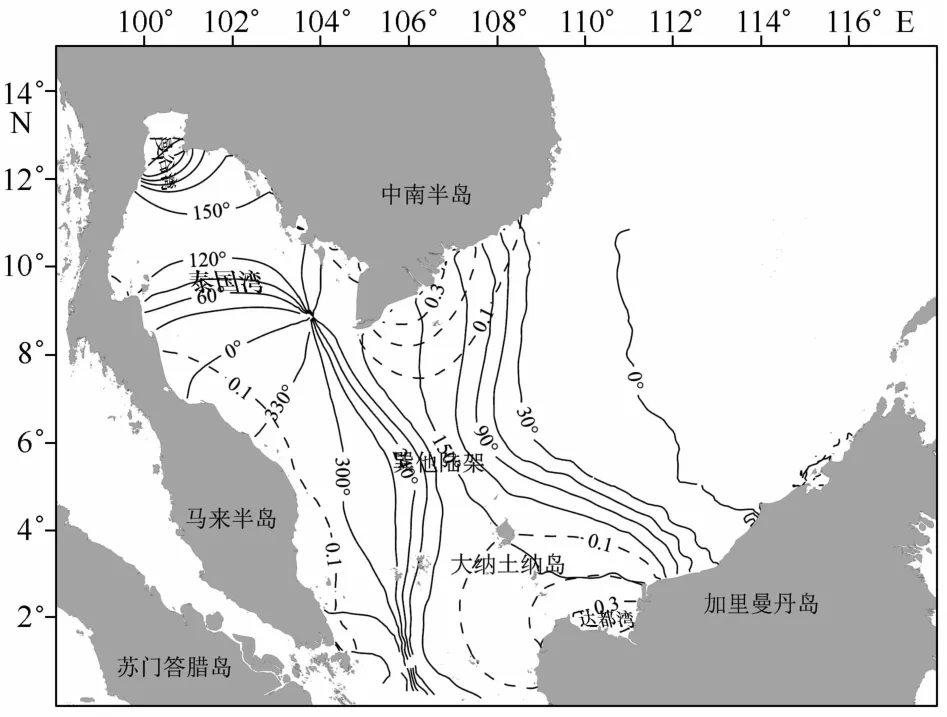
图6 S2分潮同潮图Fig.6 Predicted cotidal chart for S2
4.2潮流分布
图7给出K1和M2分潮的潮流椭圆分布,图中阴影部分表示逆时针旋转,并采用相同标尺。可以看出两个分潮的旋转方向分布基本一致,在深水区和泰国湾湾口处为顺时针旋转;卡里马塔海峡以南的逆时针旋转区成南北向的条带分布,泰国湾除湾口大部分海区也呈逆时针旋转。
K1分潮在达都湾附近和泰国湾湾口为旋转流,其他大部分海区都以往复流为主。其中泰国湾内潮流方向基本与两岸平行,沿东南-西北方向做往复运动;卡里马塔海峡以北,潮流为东西方向的往复流。M2分潮的潮流较K1分潮小,大值区主要分布于湄公河流域以及达都湾附近,即M2分潮潮汐分布的大值区。
4.3潮余流
由四个分潮共同引起的潮余流分布见图8。泰国湾中潮余流东进西出,呈逆时针回转,其中金甄角附近余流相当强,可达5 cm/s,这与方国洪等[17]结果计算一致,另一个强流区在达都角附近,潮余流沿东岸自北向南流出。
4.4潮能通量
潮能通量强度又叫做能通量密度,表示单位时间内通过单位宽度的垂直断面的潮能通量,其计算公式为:

式中,Φ和T分别为相应分潮的潮能通量密度和潮波周期;ρ为海水密度,本文取1 025 kg/m3。
本文根据式(3)及前文结果,计算K1和M2分潮的潮能通量密度,并绘制潮能通量密度分布(见图9),其中填充色表示潮能通量大小,矢量箭头表示能通量方向。K1分潮的潮能从南海进入后分为两支,一支向南从卡里马塔海峡流出,另一支向西进入泰国湾,并沿泰国湾东岸传入,经过泰国湾湾顶后沿西岸传出,由于传输过程中的能量耗散,传出的能量小于传入能量。M2分潮的潮能从南海进入后亦分为两支,大部分能量传入达都湾并发生耗散,另一支则传入泰国湾;但与K1分潮不同的是,由于科氏力作用与潮波角速率之比较小,潮能在泰国湾湾口偏转缓慢,沿泰国湾西岸传输,到达东岸后一支沿逆时针方向扫过湾顶,另一支则传向湾口。
5 结论
本文利用FVCOM海洋数值模式,建立了泰国湾及周边海域的二维潮汐数值模型,同时对K1、O1、M2和S2四个主要分潮进行模拟。研究发现采用现有的数字水深资料不能合理地模拟泰国湾潮波的基本结构,利用海图水深代替泰国湾的现有数字水深显著改善了模拟结果。计算结果与47个验潮站资料符合良好,说明结果可信。
在模式结果的基础上,对计算海域的潮汐、潮流以及潮能通量进行研究,结论如下:
(1)K1和O1分潮潮波由泰国湾东侧进入、西侧传出,湾内形成一个逆时针的旋转潮波系统;

图7 潮流椭圆分布图Fig.7 Tidal current ell ipses
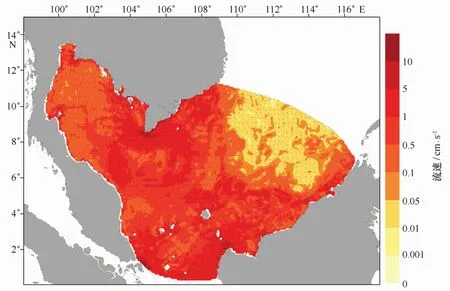
图8 潮余流分布图Fig.8 Tidal residual currents
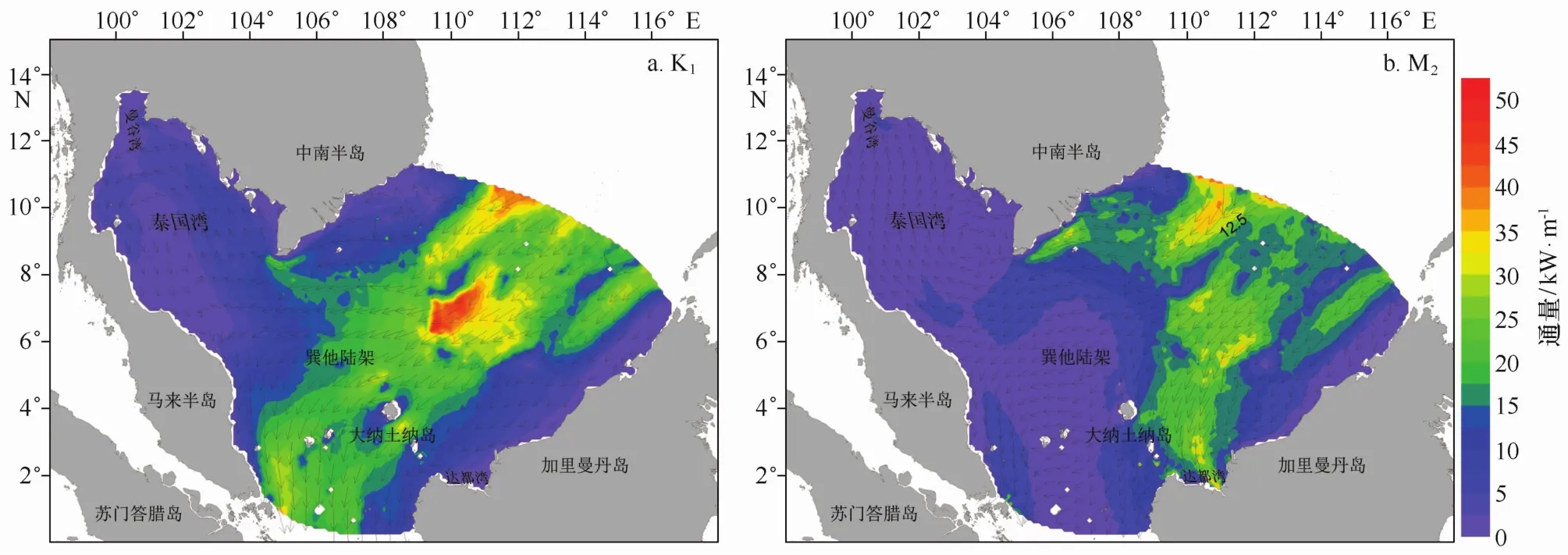
图9 潮能通量分布图Fig.9 Tidal energy flux density vectors

(2)M2和S2分潮在泰国湾湾口存在顺时针方向的旋转潮波系统。由于湾口处潮波自东北向西南传播,迫使湾内潮波按顺时针方向旋转。同时由于泰国湾所处纬度较低科氏力不足以形成逆时针方向旋转潮波。相应地潮能沿泰国湾西侧进入湾内,一支沿东岸流出,一支沿东岸进入湾顶,因此形成了与北半球一般规律相悖的顺时针旋转潮波系统;
(3)M2和S2分潮在泰国湾湾顶的无潮点向西岸发生退化;
(4)M2和S2分潮在大纳土纳岛附近不存在无潮点;
(5)在泰国湾内半日潮以旋转流为主,全日潮以往复流为主;
(6)泰国湾中潮余流东进西出,呈逆时针回转。
[1]Dietrich G.Die Gezeiten Des Weltmeeres Als Geographische Erscheinung[J].ZGesamte Erdk,1944,3:69.
[2]Defanta.Physical Oceanography[M].New York:Pergamon Press,1961:590.
[3]Ye AL,Robinson IS.Tidal dynamicsin the South China Sea[J].GeophysicalJournal of The Royal Astronomical Society,1983,72(3):691-707.
[4]俞慕耕.南海潮汐特征的初步探讨[J].海洋学报,1984,6(3):293-300.
Yu Mugeng.Prel iminary discussion on tidal characteristic of South China Sea[J].Acta Oceanologica Sinica(in Chinese),1984,6(3):293-300.
[5]丁文兰.南海潮汐和潮流的分布特征[J].海洋与湖沼,1986,17(6):468-480.
Ding Wenlan.Distribution of tides and tidal currents in the South China Sea[J].Oceanologia et Limnologia Sinica,1986,17(6):468-480.
[6]Fang GH.Tide and tidalcurrent chartsfor the marginalseas adjacentto China[J].Chinese Journal of Oceanology and Limnology,1986,4(1):1-16.
[7]Yanagi T,Toshiyuki T.Clockwise phase propagation ofsemi-diurnaltidesin the Gulf of Thai land[J].Journal of Oceanography,1998,54(2):143-150.
[8]Fang GH,Kwok YK,Yu KJ,et al.Nu merical simulation of principaltidal constituentsin the South China Sea,Gulf of Tonkin and Gulf of Thailand[J].Continental Shelf Research,1999,19:845-869.
[9]Cai SQ,Long XM,Liu HL,et al.Tide model evaluation under different conditions[J].Continental Shelf Research,2006,26(1):104-112.
[10]Zu TT,Gan JP,Erofeeva SY.Nu mericalstudy ofthe tide and tidal dynamicsin the South China Sea[J].Deep-Sea Research PartI,2008,55(2):37-154.
[11]吴頔.泰国湾潮汐潮流的数值模拟与理论模型研究[D].青岛:国家海洋局第一海洋研究所,2013.
Wu Di.Study on tide and tidalcurrentin the Gulf of Thai land based on numericalsimulation and theoretical models[D].Qingdao:The FirstInstitute of Oceanography,State Oceanic Adiministration,2013.
[12]毛庆文,齐义泉,施平,等.在南海南部大纳土纳岛附近存在S2分潮的无潮点吗?[J].科学通报,2006,51(增刊):23-26.
Mao Qingwen,Qi Yiquan,Shi Ping,et al.Isthere a S2tidalamphidromic point near Natuna Besarin the South China Sea[J].Chinese Science Bulletin,2006,51(2),23-26.
[13]Chen CS,Beardsley RC,Cowles G.An unstructured grid,finite-volu me coastal ocean model FVCOMuser manual[R].SMAST/UMASSD,2006:6-8.
[14]Pawlowicz R,Beardsley B,Lentz S.Classicaltidal harmonic analysisincluding error estimatesin MATLABusing T_TIDE[J].Computers and Geosciences,2002,28:929-937.
[15]Cheng YC,Andersen OB.Multimission empirical ocean tide model ing for shal low waters and polar seas[J].Journal of Geophysical Research,2011,116(C11001).
[16]Cu m mins PE,Oey LY.Simulation of barotropic and barocl inic tides of Northern British Colu mbia[J].Journal of Physical Oceanography,1997,27(5):762-781.
[17]方国洪,曹德明,黄企洲.南海潮汐潮流的数值模拟[J].海洋学报,1994,16(4):1-12.
Fang Guohong,Cao Deming,Huang Qizhou.Nu mericalsimulation oftides and tidalcurrentsin the South China Sea[J].Acta Oceanologica Sinica,1994,16(4):1-12.
[18]吴頔,方国洪,滕飞,等.基于双矩形海湾模型的泰国湾潮汐潮流研究[J].海洋科学进展,2013,31(4):465-477.
Wu Di,Fang Guohong,Teng Fei,et al.Study on tide and tidal currentin the Gulf of Thai land based on a two-rectangular-gulf model[J].Advancesin marine science,2013,31(4):465-477.
P731.23
A
0253-4193(2015)01-0011-10
2014-03-10;
2014-05-23。
国家自然科学基金(40676009);中央级公益性科研院所基本科研业务费专项资金资助项目(2014G15);国家国际科技合作项目(2010DBF23580);国家自然科学青年基金(40606006);青岛市科技计划基础研究项目(11-1-4-98-jch);中央级公益性科研院所基本科研业务费专项资金资助项目(2007-31)。
吴頔(1987—),女,福建省永春县人,主要从事海洋潮汐、潮流和海岸泥沙动力研究。E-mai l:wudi@fio.org.cn
方国洪(1939—),男,浙江省瑞安市人,研究员、中国工程院院士,主要从事海洋潮汐、环流和海洋数值建模研究。E-mai l:fanggh@fio. org.cn

