Kevlar绳索非对称迟滞模型及参数识别

易 琳,王 班,郭吉丰

（浙江大学电气工程学院,浙江杭州310027）

Kevlar绳索非对称迟滞模型及参数识别

易 琳,王 班,郭吉丰

（浙江大学电气工程学院,浙江杭州310027）

针对Kevlar绳索准静态加载下出现的非对称迟滞效应,建立能够灵活控制迟滞环形状的推广Bouc-Wen模型以描述高度非对称的迟滞现象.结合数学模型与试验结果特点提出适用于该模型的分步参数识别方法,通过提出的识别方法得到试样模型参数,采用数值计算方法求解模型得到在循环载荷作用下的理论迟滞曲线.结果表明,理论计算值与试验值较吻合,证明了模型的正确性与识别方法的有效性.

迟滞效应；Bouc-Wen模型；Kevlar绳索；参数识别

合成纤维是一种具有高比模量、高比强度和低伸长率的工程材料,由其制作的绳索结构在航空航天、机械、电力和电子工业中得到越来越广泛的应用.其中以Kevlar和Twaron为代表的芳香族聚胺纤维［1］有着优异的机械性能、热性能和化学性能,非常适合于航空航天领域应用,如抗空间碎片碰撞结构、降落伞绳、空间绳系系统等［2-3］.

在对采用芳纶绳索的空间绳系卫星系统进行动力学分析及控制时,考虑卫星刚体动力学模型的同时,还须考虑连接卫星绳索的力学模型.以往的研究多以弹簧阻尼模型来描述绳索的力学行为［4］,该类模型相对简单,有利于降低控制器设计的复杂性和提高计算效率,但在描述绳索的一些非线性特性时与实际相差较大.Cheng等［5］在对单根Kevlar KM2纤维的机械特性研究中,采用实验方法测得了本构关系在纵向、横向以及扭转方向的5个独立参数,对由多根纤维加捻编织而成的绳索特性研究有一定的参考意义.Shim等［6］研究由Twaron纤维制作的盔甲面料动态力学性能,发现材料在高应变速率与低应变速率作用下相比强度和弹性模量均显著增大,采用黏弹性开尔文模型解释了这一现象.Chailleux等［7］提出芳纶纱线的非线性黏弹性和黏塑性拉伸行为的数学模型,指出纱线在小形变范围内具有非线性应力-应变关系,描述了恒应力下纱线的拉伸蠕变规律和最大应力相关的塑性变形正向积累规律.迟滞效应是指在载荷作用下材料的受力和形变之间表现出具有记忆特征的迟滞时变关系,Bouc于1967年提出一种光滑迟滞模型,后经Wen［8］改进得到能够产生系列不同迟滞曲线的模型,用以描述大量存在于机械、土木、地震和材料等工程中的迟滞现象.笔者在对Kevlar绳索的准静态受力—形变关系进行实验研究时发现,绳索不仅表现出蠕变、非线性刚度和阻尼、塑性变形等非线性现象,而且在周期往复加减载时表现出明显的迟滞效应.这给绳索动力学模型的建立带来了新的挑战,然而关于Kevlar绳索的迟滞非线性特性的研究鲜有文献报道.

Kevlar绳索迟滞效应产生的机理较复杂,不仅在微观上与材料本身的分子结构有关,而且在宏观上与纤维加捻捻度及缠绕并线方式有关,因此很难从迟滞效应产生机理上来建立迟滞特性模型.本文对Kevlar绳索的轴向恢复力-形变关系进行试验研究,得到静态加载方式下的恢复力-形变迟滞曲线,对测得曲线的观察分析发现,其为非对称迟滞曲线.基于原始Bouc-Wen对称模型的滞环形状分析,提出一种推广Bouc-Wen模型描述非对称迟滞现象.采用适合该模型的分步识别方法识别出模型中的各参数值,根据识别得到的参数代入模型进行数值计算,与试验曲线进行对比,以验证建立模型的准确性及参数识别方法的有效性.

如无特别说明,本文所述绳索形变及恢复力均沿绳索轴向,在准静态加载条件下仅研究纵向形变与恢复力的关系.

1 Kevlar绳索非对称迟滞模型

图1 Kevlar绳索试样实物Fig.1 Specimen of Kevlar tether

Kevlar材质绳索如图1所示,绳索由3股纱线并线缠绕而成,每股纱线由若干根纤维单丝加捻而成,试样直径为1.5 mm,总长度为18.1 m,断裂拉力约为1 300 N.未经加载的Kevlar绳索在循环加载后会产生一定的残余形变,该形变在卸载后无法恢复,且残余形变与加载历史中的最大负载呈正相关,即最大负载越大残余形变量越大,Chailleux等［7,9］对Kevlar材料的这种特性进行研究.其成因在于芳族高分子间形成的分子链在拉力作用下发生旋转,导致材料发生塑性变形,此外,绳索结构内部存在间隙,经过拉力拉伸后结构内部间隙变小,且该变化不可逆.该现象类似于填充橡胶材料的马林斯效应［10］.为了研究Kevlar绳索的迟滞特性,须消除塑性变形的影响,故在试验之前对试样施加合适的预载荷,保持足够长时间直至绳索的形变量不再增加.试验通过试样一端固定,另一端悬挂系列不同质量重物的方式测量周期载荷作用下绳索形变量与恢复力的关系.测量的难点主要在于如何非接触地精确测量微小形变,避免测量设备的摩擦力作用干扰对绳索施力.试验装置采用SensoPart公司生产的FT 80 RLA-500-S1L8激光位移传感器测量绳索伸长量,传感器量程为500 mm,分辨率为0.5 mm.通过RS485通讯将采集的位移数据传输至计算机存储和处理,试验装置原理如图2所示.图中,x为形变,F为恢复力.试样在进行迟滞特性测量试验前经过持续12 h的85 N轴向预加载,所有试验均在恒定室温（20℃）的条件下进行.

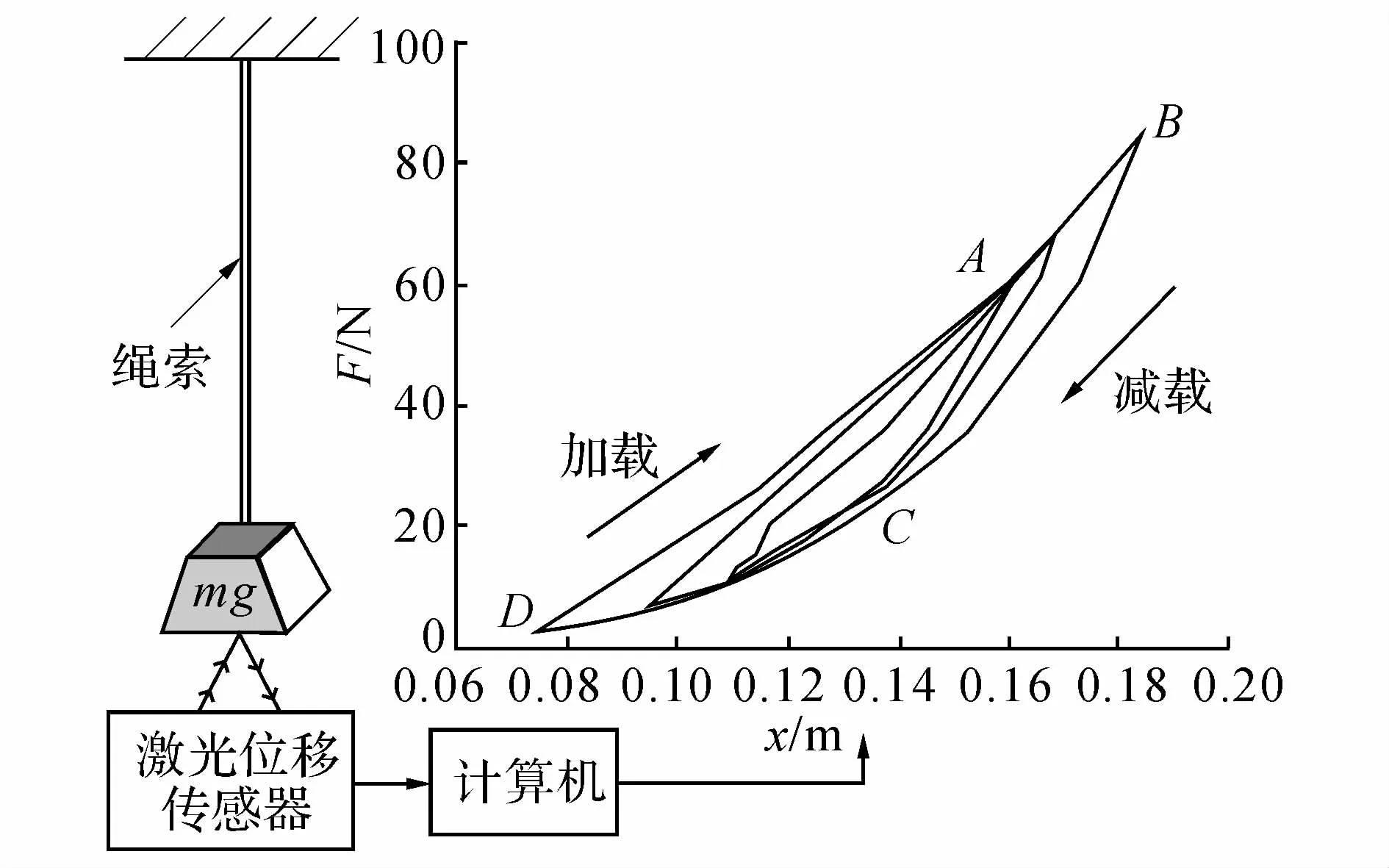
图2 Kevlar绳索迟滞特性试验装置原理图及试验结果Fig.2 Experiment set and result on hysteresis effect of Kevlar tether

1.1 Bouc-Wen模迟滞形状控制

试验结果表明,Kevlar绳索在准静态加载下的轴向受力和形变关系具有较明显的迟滞现象,表明绳索的形变不仅与受力有关,还与受力历史过程有关,是典型的非线性时变系统,不能用简单的非线性弹簧模型描述.Bouc-Wen模型具有通用性及便于数学处理等优点,因而被广泛地应用于描述非线性迟滞系统,物理模型如图3所示.

该模型能够从现象上解释和反应局部记忆迟滞效应,如下所示：

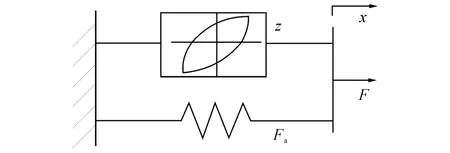
图3 恢复力物理模型Fig.3 Physical model of restoring force

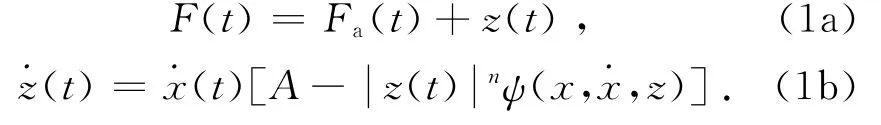
式中：t为时间,F（t）为绳索恢复力,Fa（t）为弹性恢复力,x（t）为形变量；z（t）为迟滞恢复力,是为反映迟滞特性引入的虚拟状态变量,无实际物理意义,也无法直接测量；A和n分别为控制迟滞环大小和光滑程度的常数,ψ为关于x、和z的非线性函数,控制迟滞环形状因素。通过尝试不同非线性函数,对图2的绳索恢复力和形变关系曲线进行拟合发现,曲线与三次多项式函数曲线较接近,令

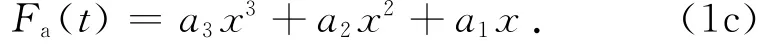
z（t）不仅与当前形变量x（t）有关,而且和加载历史过程有关；Fa（t）仅与x（t）有关,与加载历史过程无关.

对于原始的Bouc-Wen模型,有

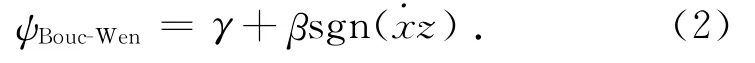
式中：γ和β为与Bouc-Wen迟滞环形状有关的常数.

式（1b）等号两边同时乘以d t／d x,可得

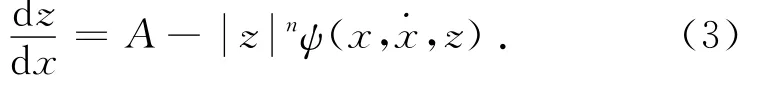
从式（3）可以看出,x-z相平面内的迟滞环斜率d z／d x由模型参数A、n及形状控制函数ψ决定,通常函数ψ的值仅与x、和z的符号有关.根据时间的物理意义有d t＞0,所以与d x的符号相同.根据式（3）可知,特别是当n≠1时,通常难以给出z关于x的解析形式,因此通过数值计算分析是有效的.

图4 形状控制函数值Fig.4 Shape control function

1.2 推广Bouc-Wen模型

绳索只能承受轴向拉力,不能承受轴向压力,相应的形变只能是拉伸形变（x＞0）.观察图2可以发现,迟滞曲线不存在与形变量x相关的几何中心,从物理意义上来说迟滞特性不以某形变值为分隔.考虑形状控制函数与x无关,对Bouc-Wen形状控制函数改进来得到在4个相位内对应不同数值的形状控制函数是亟待解决的.按照该思路,提出4自由度推广Bouc-Wen模型：

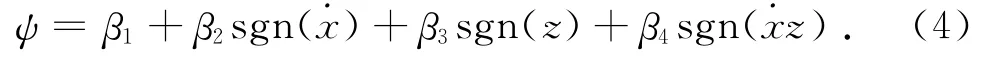
式中：β1、β2、β3和β4为常数.该形状控制函数包含4个相位,依据˙x和z的不同符号组合可以有4个不同的取值,图4（b）表示模型在一个加载周期内的非对称迟滞环.当ψ1＝ψ3且ψ2＝ψ4时,改进的非对称迟滞模型退化为Bouc-Wen对称模型,因此可以认为该模型是Bouc-Wen模型的一种推广模型.图4（b）中4个相位内ψ的取值与˙x和z的符号组合对应的关系如表1所示.

表1 推广Bouc-Wen模型ψ取值Tab.1 Values ofψfor generalized Bouc-Wen model

表1列出的ψi与βi（i＝1,2,3,4）之间的线性关系可由下式表示：

式（5）中的系数矩阵满秩,故有

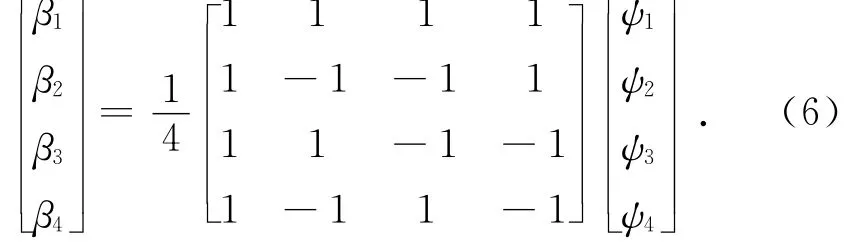
利用式（5）、（6）的矩阵方程,可以通过非线性最优化方法,拟合试验数据得到相应的ψi,最优目标为所有试验数据与理论计算值的差值平方和最小,再由式（6）计算得到βi.直接根据式（4）和试验数据可以识别出使试验数据和理论计算结果最接近的一组模型参数βi,而无需考虑ψi.前一种识别方法的优点是参数更易于识别,特别是在分段识别各相位内的ψ时.

2 非对称迟滞模型参数识别

2.1 最小二乘识别法

假定试验测得的离散数据为（xi,Fi）（i＝1,…, m）,由式（1）和（4）组合形成了Kevlar绳索的非对称迟滞恢复力模型.该模型包括9个独立参数,形成以下向量：

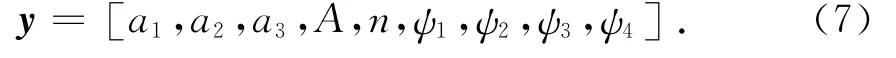
将式（1a）、（1c）代入式（3）得到模型参数识别的误差函数：

为了得到一组使理论模型计算结果最接近试验数据的模型参数,可以采用最小二乘法进行模型参数识别.将数据点（xi,Fi）（i＝1,…,m）代入式（8）,得到对应的残量：

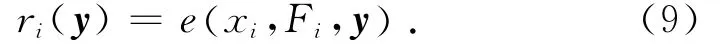
目标函数为所有数据点的残差平方和,即

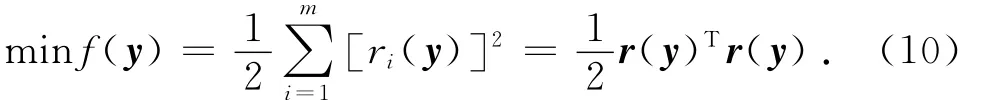
式中：r（y）为残量函数,r（y）＝［r1（y）,r2（y）,…, rm（y）］T.使式（10）最小的向量y是识别得到的参数,可以利用高斯-牛顿方法［11］求解式（10）的非线性最小二乘问题.

2.2 参数分步识别方法

吴善跃等［12］在研究钢丝绳减震器的非对称迟滞模型参数识别问题时提到,在非线性最小二乘问题求解过程中会出现矩阵病态导致识别效果不理想,提出一种具有更好识别效果的分解识别方法.本文研究的对象恢复力模型有所不同,且绳索结构有特殊性,如只能拉伸不可压缩,故须探索适合Kevlar绳索非对称迟滞模型参数识别效果更理想的方法.采用降低待识别参数向量y的维数的方法,根据参数类别结合参数在模型中所起的作用逐一识别,上一识别环节的结果作为下一环节的已知参数,直至得到参数向量中所有元素的识别结果.

2.2.1 弹性恢复力模型参数识别 从迟滞恢复力z的物理意义并根据式（3）可知,迟滞恢复力在x-z相平面有界,令d z／d x＝0,有

这表现在图2（b）中迟滞回线随x的增大逐渐接近上界zmax＝,反之逐渐接近下界zmin＝.从图2中观察到不同幅值的循环加载曲线在加载区域和减载区域各有一共同的渐进线,这2根渐近线的部分曲线段如AB和CD段所示,为迟滞恢复力z接近上、下界时形成.由式（1a）、（11）可知：

设（xABi,FABi）（i＝1,…,r）和（xCDi,FCDi）（i＝1,…,s）分别为AB和CD段内的试验数据,将数据点写成向量形式：xr＝［xAB1,xAB2,…,xABr］,Fr＝［FAB1,FAB2,…,FABr］,xs＝［xCD1,xCD2,…, xCDs］,Fs＝［FCD1,FCD2,…,FCDs］,代入式（12）有

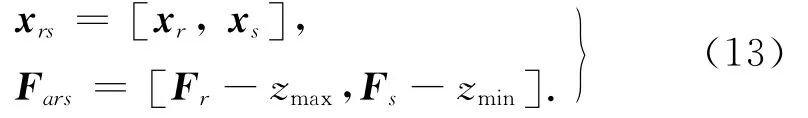
式（13）完成了对试验数据弹性恢复力部分与迟滞恢复力部分的解耦,经过处理后的数据可以直接用来识别弹性恢复力模型式（1c）.

将图2中相同横坐标x对应的加载部分FDAB与减载部分FDCB作减法运算得到的最大差值为18 N,可令zmax＝9,zmin＝－9.采用线性最小二乘识别方法：

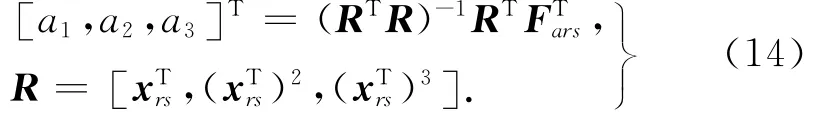
弹性恢复力模型识别结果如图5所示.

2.2.2 迟滞恢复力模型参数识别 由于迟滞恢复力无法直接测量得到,由式（1a）可知,将图5中的恢复力实测值与弹性恢复力计算值相减,可得迟滞恢复力,即zi＝Fi－＋a1xi）,计算结果如图6所示,将得到的迟滞恢复力计算结果作为迟滞恢复力测量值.

将z＝0代入式（3）,有d z／d x＝A,即根据图6中曲线在z＝0处的斜率可以求得模型参数A.对于图6中3次不同循环加载幅值下的迟滞恢复力曲线,分别求得相位4、1交越处与相位2、3交越处的斜率,再对求得的斜率求平均得到A＝380.由式（11）可知：

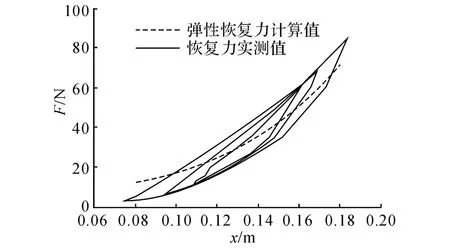
图5 弹性恢复力模型参数识别结果Fig.5 Identification result of elastic restoring force

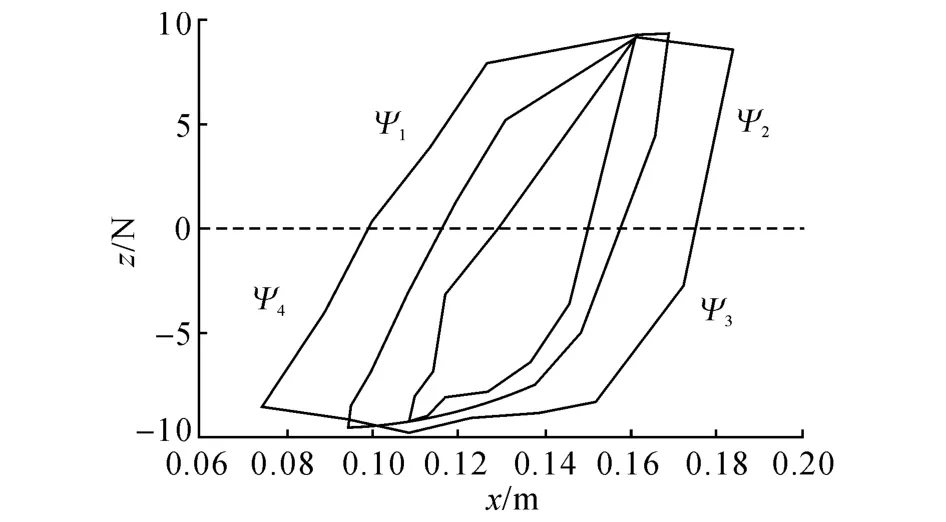
图6 迟滞恢复力测量值Fig.6 Measured values of hysteretic restoring force

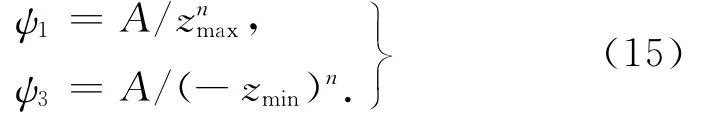
参数向量y中剩下3个待识别的元素：n、ψ2和ψ4.由图6的数据（xi,zi）（（i＝1,…,m）和式（15）,结合y中已识别得到的参数代入式（8）～（10）,导出关于3个待识别元素的非线性最小二乘问题,采用高斯-牛顿迭代方法求解得到参数识别结果：n＝2.93, ψ2＝－6.543,ψ4＝－0.113.将n代入式（15）计算得到ψ1＝0.552,ψ3＝0.552.由式（6）计算可得：β1＝－1.388,β2＝1.608,β3＝－1.608,β4＝1.940.

2.2.3 模型参数识别过程总结 识别过程如图7所示.首先要保证试验数据覆盖足够大的形变范围,以尽可能使迟滞恢复力达到“饱和”并且上下“饱和”区域对应的横坐标x上有重合.观察恢复力模型可以发现,弹性恢复力项只与形变x有关,与加载历史过程无关,迟滞恢复力项在试验结果中随x表现出单调变化且存在上界和下界.利用这一性质,可以计算出迟滞恢复力的最大、最小值zmax和zmin.根据迟滞曲线的渐近线段部分数据可以识别弹性恢复力系数a1、a2和a3.将迟滞恢复力项分离出来,迟滞恢复力为系统迟滞现象的根源,根据d z／d x在z＝0处的值识别参数A,而ψ1、ψ3可以用参数n表示.然后采用非线性最小二乘识别方法,得到参数n、ψ2和ψ4.最后根据参数βi与ψi（i＝1,2,3,4）之间的线性关系计算出βi的值,完成对模型中所有参数的识别.

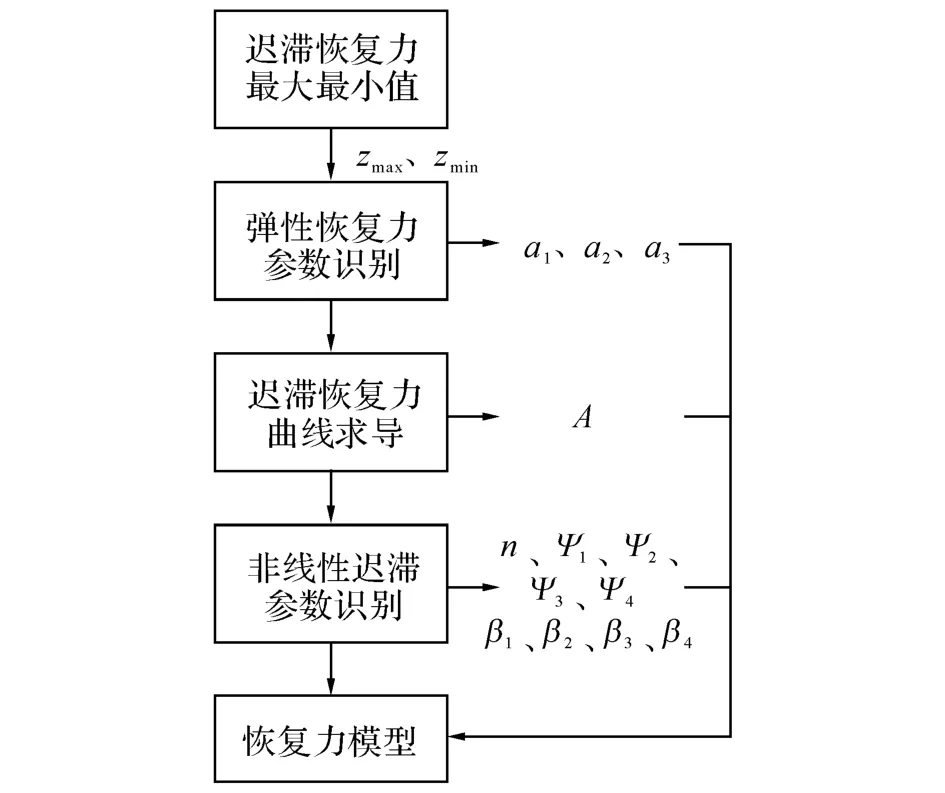
图7 推广Bouc-Wen模型参数识别过程Fig.7 Process of identification for generalized Bouc-Wen model

3 模型及其参数识别结果校验

将参数识别结果代入非对称迟滞模型式（1）和（4）,可得

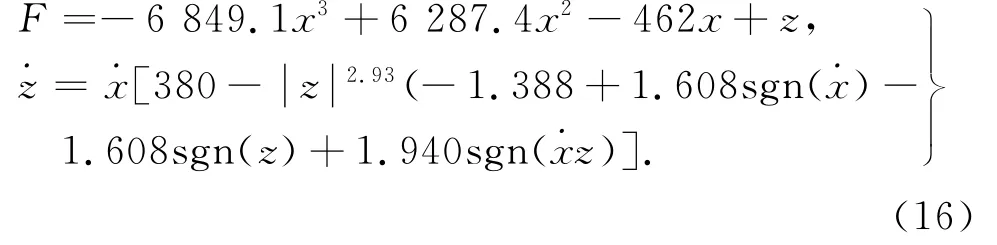
针对图2所示的测试系统,需要考虑重物自身的动力学模型：

式中：m为重物质量,试验时通过改变重物质量来实现加载或减载；g为重力加速度,取9.8 m／s2.

以重物质量m作为系统输入,重物重力周期变化且幅值在每2个周期减小一次,以模拟实际加载过程,如图8所示.对式（16）、（17）进行数值计算,模拟在循环加载条件下F与x间的变化关系,仿真计算结果与试验结果对比如图9所示.图9表明,采用提出的非对称迟滞模型能够反映试样的迟滞特性,利用该模型来描述Kevlar绳索在静态加载下的恢复力-形变关系是适合的；模型的仿真计算值与实测值比较吻合,证明提出的分步参数识别方法能够根据循环加载试验结果有效地识别出模型参数.

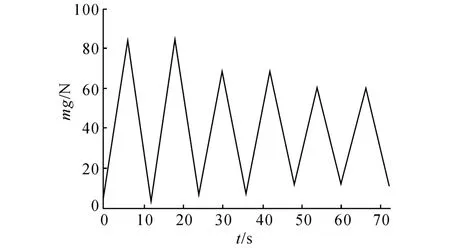
图8 非对称迟滞仿真模型输入Fig.8 Simulation input of asymmetric hysteresis model

图9 非对称迟滞模型仿真计算结果与试验结果Fig.9 Simulation result of asymmetric hysteresis model compared with experimental data

4 结 语

Kevlar绳索在工程应用中表现出强非线性,特别是大尺度的强能量耗散.本文针对其准静态加载情况下轴向恢复力与形变关系表现出的非对称迟滞现象,基于对工程领域应用广泛的Bouc-Wen模型形状控制分析,提出一种推广的Bouc-Wen模型.该模型包括4个独立的形状控制参数,能够分别控制迟滞环4个不同相位内的形状,灵活地描述各种不同形状的非对称迟滞现象.提出适合Kevlar绳索特性的参数分步识别方法.将参数识别的结果代入数学模型,得到相应的计算值,与实测值相比较吻合.证明采用该模型描述Kevlar绳索的非对称迟滞特性是合适的,提出的识别方法能够有效地识别该模型的各参数,可为类似的芳纶材料编织绳带结构迟滞特性研究提供参考.

［1］YANG H H.Kevlar aramid fiber［M］.New York：Wiley,1993.

［2］SPENCER D A,BLANCHARD R C,BRAUN R D,et al.Mars Pathfinder entry,descent,and landing reconstruction［J］.Journal of Spacecraft and Rockets,1999, 36（3）：357- 366.

［3］刘滨涛,贾光辉,黄海.Kevlar层合板超高速撞击数值建模及参数识别［J］.宇航学报,2011,32（02）：261- 266.

LIU Bin-tao,JIA Guang-hui,HUANG Hai.Numerical modeling and parameter identification for Kevlar laminate under the condition of hypervelocity impact［J］.Journal of Astronautics,2011,32（02）：261- 266.

［4］SEBASTIAN M S,UNNIKRISHNAN K C,NARAYANAN S.Viscoelastic properties of Kevlar-29 fabric tape strength member［J］.Mechanics of Materials, 2008,40（11）：949- 960.

［5］CHENG M,CHEN W N,WEERASOORIYA T.Mechanical properties of Kevlar（R）KM2 single fiber［J］.Journal of Engineering Materials and Technology：Transactions of the ASME,2005,127（2）：197- 203.

［6］SHIM V P W,LIM C T,FOO K J.Dynamic mechanical properties of fabric armour［J］.International Journal of Impact Engineering,2001,25（1）：1- 15.

［7］CHAILLEUX E,DAVIES P.Modelling the non-linear viscoelastic and viscoplastic behaviour of aramid fibre yarns［J］.Mechanics of Time-Dependent Materials, 2003,7（3／4）：291- 303.

［8］WEN Y K.Method for random vabration of hysteretic systems［J］.Journal of the Engineering Mechanics Division-ASCE,1976,102（2）：249- 263.

［9］CHENG M,CHEN W N.Modeling transverse behavior of Kevlar（R）KM2 single fibers with deformation-induced damage［J］.International Journal of Damage Mechanics,2006,15（2）：121- 132.

［10］MULLINS L.Softening of rubber by deformation［J］.Rubber Chemistry and Technology,1969,42（1）：339- 362.

［11］王宜举,修乃华.非线性最优化理论与方法［M］.北京：科学出版社,2012.

［12］吴善跃,朱石坚.钢丝绳减振器非对称迟滞模型的参数分解识别研究［J］.振动工程学报,2007,20（06）：613- 616.

WU Shan-yue,ZHU Shi-jian.Separated identification of asymmetric hysteretic model parameters for a wirecable vibration isolator［J］.Journal of Vibration Engineering,2007,20（06）：613- 616.

Modeling and identification of asymmetric hysteresis for Kevlar tether

YI Lin,WANG Ban,GUO Ji-feng
（College of Electrical Engineering,Zhejiang University,Hangzhou 310027,China）

A generalized Bouc-Wen model with flexible shape control was proposed to describe the asymmetric hysteresis effect of Kevlar tether under quasi-static loading.An appropriate method to identify the model parameters step by step was developed by combining the mathematical model with the features of the experimental data.Theoretical curve under cyclic load was calculated using numerical method.Results showed that the experimental data fitted well with the theoretical curve,which verified the correctness of the model and the validity of the identification method.

hysteresis effect；Bouc-Wen model；Kevlar tether；identification of parameter

10.3785／j.issn.1008-973X.2015.07.024

TB 332；TB 125

A

1008- 973X（2015）07- 1376- 06

2014- 06- 27. 浙江大学学报(工学版)网址：www.journals.zju.edu.cn／eng

国家“863”高技术研究发展计划资助项目（2013AA7044026）；国家自然科学基金资助项目（51475411）.

易琳（1986－）,男,博士生,从事空间绳系机构及控制技术的研究.E-mail：yilinyiluo＠163.com

郭吉丰,男,教授.E-mail：gjf＠zju.edu.cn