面向Web服务QoS预测的非负矩阵分解模型

苏 凯,马良荔,孙煜飞,郭晓明

（1.海军工程大学装备经济管理系,湖北武汉430033；2.海军工程大学计算机工程系,湖北武汉430033）

面向Web服务QoS预测的非负矩阵分解模型

苏 凯1,2,马良荔2,孙煜飞2,郭晓明2

（1.海军工程大学装备经济管理系,湖北武汉430033；2.海军工程大学计算机工程系,湖北武汉430033）

针对目前QoS预测算法准确度不高的问题,提出通过挖掘已有QoS观测数据中的近邻信息和隐含特征信息而实现服务QoS预测的方法.建立QoS预测的矩阵分解因子模型,将QoS预测问题转化为稀疏QoS矩阵下的模型参数期望最大化（EM）估计问题,提出结合近邻信息的非负矩阵分解算法NCNMF＋EM对该问题进行求解.算法综合利用了QoS矩阵中的近邻信息和隐含特征信息,可以实现对不同类型QoS属性值的准确预测.实验结果表明,采用该方法可以显著地提高服务QoS的预测准确度,且算法的运行时间随着矩阵规模的增大呈线性增长,可以应用于大规模的QoS预测问题中.

Web服务；服务选择；QoS预测；矩阵因子模型；非负矩阵分解；期望最大化估计

随着Web服务技术的发展,网络上出现大量满足相同功能、但服务质量（quality of service,QoS）不同的候选服务,QoS逐渐成为用户评价Web服务,进而选择服务的重要依据［1-3］.在实际应用中,由于不同用户在调用服务时,网络环境、地理位置和服务运行环境等存在差异,导致他们体验到的服务QoS不同［4］.用户需要对候选服务的QoS进行准确的预测,从而为Web服务的选择提供可靠的QoS数据支撑.

目前,许多QoS驱动的服务选择算法［5-7］均采用统计平均法预测服务的QoS,该方法将服务的QoS历史平均值作为预测值统一提供给用户,未考虑用户的个性化差异,导致预测准确率较低.Shao等［8］认为“对某些服务拥有相似QoS经验的用户,对其他服务的QoS体验也会比较接近”,进而采用协同过滤推荐方法为用户个性化地预测服务的QoS.Zheng等［9］提出一种混合协同过滤QoS预测方法WSRec,通过综合基于用户和基于服务的协同过滤预测结果,使得QoS信息矩阵中的近邻信息得到更充分利用.协同过滤方法对于用户评分等主观型数据的预测较准确,但服务的QoS是一种受环境因素影响较大的客观型数据,仅通过挖掘QoS数据中的近邻信息难以保证QoS预测的准确度.

文献［10,11］假设“当外界环境特征和输入特征相似时,服务的QoS相对稳定”,进而在为目标用户预测服务的QoS时,首先探测用户的环境特征和输入特征等,然后在特征库中搜索特征相似的QoS使用信息,并以此为基础进行协同过滤预测.和传统的协同过滤方法相比,该方法的预测效率和准确率都有一定的提升,但是该方法在预测QoS前大多假设特征库已经建立好,且特征库中已存在大量的特征QoS信息,否则难以保证QoS的预测准确度.在实际中影响服务QoS的环境特征因素很多,很难建立完备的特征QoS信息库,因此该类方法面临较大的应用困难.

Zheng等［12-14］认为用户对服务的QoS体验由少量隐含因子决定,提出建立合理的矩阵因子分解模型对已有的QoS观测数据进行拟合,从而挖掘出影响用户QoS体验的隐含特征,进而为用户提供个性化的QoS预测.与文献［10,11］中建立显式的特征模式不同,矩阵分解模型技术从已有的QoS观测数据出发,挖掘观测数据中包含的隐含特征,算法实现简单,有效性高,更适用于现实中的大规模服务QoS预测问题.Zheng等［12-14］将矩阵因子分解问题转化为损失函数的最优化问题,采用梯度下降法进行求解,不足之处在于算法收敛速度较缓慢,且收敛结果对于迭代步长的选择较灵敏.

本文提出一种通过挖掘已有QoS观测数据中的近邻信息和隐含特征信息而实现服务QoS预测的方法.首先假设QoS观测数据产生于一个低维线性模型和高斯噪声的叠加,进而将稀疏QoS矩阵下的QoS预测问题转化为模型参数的EM估计问题,然后提出一种结合近邻信息的非负矩阵分解算法NCNMF＋EM对该问题进行求解.由于算法综合利用了QoS矩阵中的近邻信息和隐含特征信息,可以实现对不同类型QoS属性值的准确预测.

1 QoS预测模型

QoS是描述Web服务质量的一系列非功能属性的集合,通常包括价格、响应时间、吞吐量、可靠性和可用性等.假如QoS预测系统包含n个服务和m个用户,则服务的QoS使用信息可以采用n×m的用户-服务QoS矩阵R表示,矩阵R中的任意项Rij表示用户j调用服务i时的QoS值.在现实中,大部分用户只调用过少量的服务,因此QoS矩阵R包含许多缺失项,预测系统的目标是利用R中的已知QoS信息对这些缺失项进行准确的预测.例如,当用户j未调用服务i时,则QoS矩阵中的Rij为缺失项,需要对这些缺失项进行预测.

笔者希望通过矩阵因子分解模型技术找到一个低维线性模型X＝UV对QoS矩阵R进行逼近,则缺失项Rij的预测值可以通过U的第i行与V的第j列取向量内积得到.其中U为n×k矩阵,V为k×m矩阵,k为特征因子的个数.

QoS矩阵因子分解模型具有一定的物理意义.假设服务的QoS可以由隐含的k个特征因子决定,这些特征因子可以是网络环境特征、服务器环境特征和用户输入特征等.具体来说,网络环境特征可以包含网络带宽、网络吞吐量等,服务器环境特征可以包含服务器的CPU利用率、内存利用率、进程占有率、并发访问率等,用户特征可以包含用户输入大小、任务类型、地理位置等.假如对于每个特征因子,都对服务的QoS值有固定的影响基准值,比如对于某个信用卡号验证服务,QoS（如响应时间）受输入的信用卡号数量影响较大,而受所处的地理位置和网络吞吐量影响较小,因此可以认为对于该服务,用户输入特征的QoS影响基准值较高；对于某个视频传输服务,用户位置离服务器越远、网络吞吐量越低,则用户体验到的服务响应时间越长,因此对于该类服务,用户位置和网络吞吐量的QoS影响基准值较高.将模型中的U称为QoS基矩阵,并将U写成列向量形式U＝［U1,U2,…,Uk］,则Ud（d＝1,2,…,k）表示第d个特征因子对各个服务的QoS影响基准值；V称为权重矩阵,每一列对应为某个用户对这k个特征因子赋予的权重,反映了该用户对这些特征因子的敏感程度.用户j对服务i的QoS体验值可以表示为服务i在这k个特征因子上的QoS基准值的某个线性组合,系数为用户j对相应特征因子赋予的权重值,如下所示：

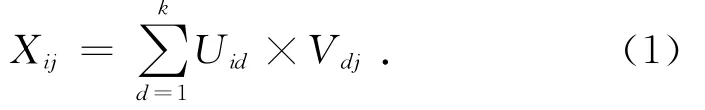
式中：Xij为用户j对服务i的QoS估计值,Uid为第d个特征因子对服务i的QoS基准值,Vdj为用户j对第d个特征因子赋予的权重.

QoS属性值（如响应时间、吞吐量、可靠性、可用性等）通常是非负的,所以U中的元素应满足非负性约束.根据前面假设可知,用户对服务的QoS体验值为一系列对特征因子的QoS基准值的线性组合,即用户对服务的整体QoS感知,由对各个特征因子的局部感知组合而成.为了更好地表征整体是由局部组成的这一直观认识,V中的元素也应满足非负性约束.与文献［12,15,16］类似,假设用户对服务的QoS体验值可以由一个低维线性模型和高斯噪声的叠加得到,即R＝X＋Z,Z为噪声矩阵, Zij满足期望为0、标准差为σij的高斯分布.QoS预测的矩阵因子分解模型由下式表示.

为了简化问题,假设高斯噪声的标准差σij均取统一常量σ,则Rij满足期望为Xij、标准差为σ的高斯分布,记为Rij～N（Xij,σ2）.由以上定义可知, Xij是未知的参数,须对其进行估计.

2 QoS预测模型的参数估计

假设用户调用不同服务体验到的QoS值是独立的,即QoS矩阵R的每个元素是统计独立的,则对于QoS观测矩阵R,变量X的似然函数为

由1章可知,Rij～N（Xij,σ2）,则Rij的概率密度函数为

等式两边取对数,可得对数似然函数：

假如R中的观测数据是完整的,即不含缺失项时,则可以采用极大似然估计法估计模型参数X.

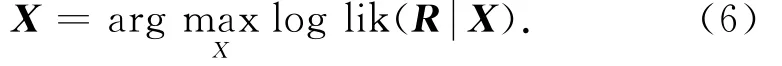
在现实应用中,绝大部分用户只对其中少量服务有过调用经历,因此用户-服务QoS矩阵R是包含大量缺失项的稀疏QoS矩阵.鉴于此,采用EM算法最大化QoS矩阵中已知观测数据的似然函数,以获取模型参数X的估计.EM算法通常用于在不完整数据条件下的参数最大似然估计［17-18］.EM算法在每次迭代时包含2个步骤：E步,利用对隐含变量的现有估计值,计算完整数据的对数似然函数的期望；M步,通过最大化在E步求得的期望得到当前的参数估计值,将该估计值用于下一次迭代中的E步.通过交替执行这2个步骤,使模型参数收敛.

将QoS矩阵R中的已知观测数据和未观测数据分别定义为Ro和Ru,假设EM算法在第t次迭代后获得的X的估计值为Xt,则在第t＋1次迭代时,包含以下2个步骤.

1）E步：计算完整QoS矩阵数据的对数似然函数的期望,记为

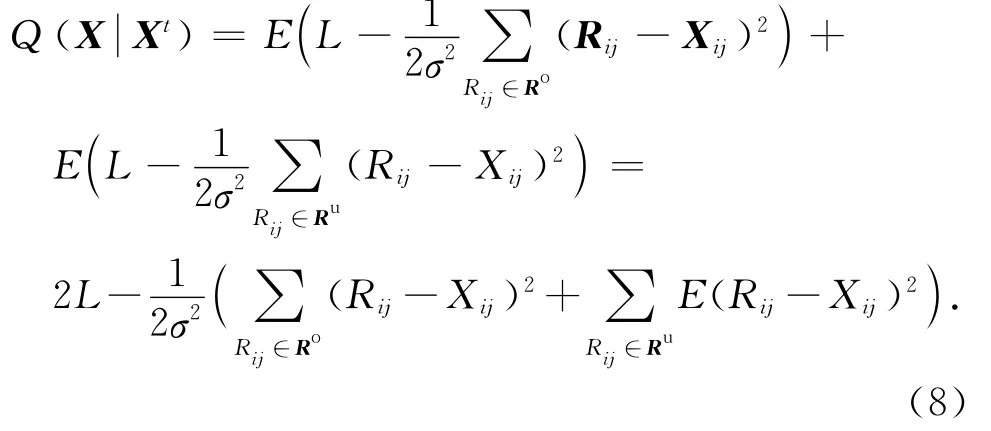
对于∀Rij∈Ru,Rij～N（,σ2）,可得

将式（9）代入式（8）,并令Ru中的元素个数为C,可得

2）M步：通过最大化Q（X Xt）来获得当前X的估计值.

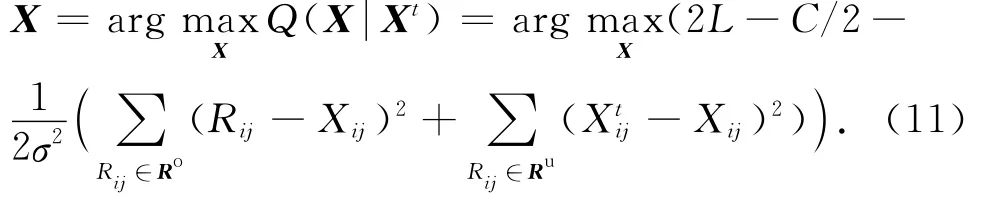
m、n、σ和C均为常量,因此

令矩阵Rt＋1表示第t＋1次EM迭代时的完整矩阵,其中缺失项Rij∈Ru采用第t次迭代时的模型估计值X填充,将式（1）代入式（12）,可得

式中：·F表示矩阵的Frobenius范数.

由式（13）可知,可以通过寻找非负QoS基矩阵U和权重矩阵V使得 Rt＋1－UV2F最小,得到当前M步X的估计值.假如将 Rt＋1－UV2F作为目标函数,则可以通过对Rt＋1进行非负矩阵因子分解（NMF,non-negative matrix factorization）求解U和V.NMF最早由Lee等［19］提出用于提取人脸图像的局部特征和文本中的语义特征,通过将非负矩阵分解为2个低维非负矩阵的乘积,挖掘原始矩阵的局部特征,实现对高维原始矩阵的降维拟合.对Rt＋1的NMF操作步骤如下.首先产生非负随机数作为U和V的初始值,然后采用Lee等［20］提出的乘性更新法则,迭代求解U和V：

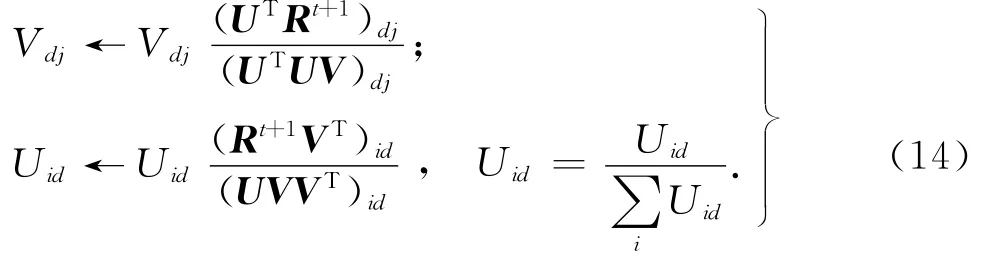
Lee在文献［20］中证明了在该迭代规则下,目标函数 Rt＋1－UV单调不增,并在若干次迭代后趋于收敛,且矩阵U和V的非负性可以得到保证.

通过对Rt＋1的NMF操作,可得Rt＋1的逼近矩阵UV,从而得到当前M步X的估计值X＝UV.该估计值将被用于下一次EM迭代中的E步计算中.

综上可知,采用EM算法估计参数X包含如下步骤：首先对X赋初始值,然后在每次迭代的E步中使用X对稀疏QoS矩阵R中的缺失项进行填充,在M步中对填充后的完整矩阵R进行非负矩阵分解,得到R的逼近矩阵UV,以此更新X并用于下一次迭代中的E步.该过程不断重复,直到X收敛于某个局部最优值.

3 QoS预测算法NCNMF＋EM

矩阵分解模型难以检测到相似用户或者相似服务之间的关联关系［12］.实际上,充分挖掘出这种近邻关系,并用于NMF的求解过程,可以有效提高对QoS的预测准确度.尤其当QoS矩阵非常稀疏时,单独采用NMF方法或近邻法都难以保证较优的预测准确度.本节提出一种结合近邻信息的非负矩阵分解算法NCNMF＋EM（neighbor information combined non-negative matrix factorization with EM procedures）,以实现稀疏QoS矩阵下的模型参数EM估计.算法首先采用基于服务的最近邻协同过滤法预测原始QoS矩阵R中的缺失QoS,得到完整的QoS矩阵,并将该完整矩阵作为2章所述的EM算法中模型参数X的初始估计值；然后采用NMF算法更新X,通过交叉执行E步和M步,使X趋于收敛,则R中缺失项的预测值即为X中的对应项.算法由于在模型参数的EM估计中引入了近邻先验信息,可以有效地提高EM算法的收敛速度和最终收敛值,从而保证了算法的QoS预测准确度和预测效率.NCNMF＋EM算法的具体描述如下.

算法1 NCNMF＋EM.

输入：稀疏QoS矩阵R,R中的未观测数据集Ru,特征因子个数k,最近邻数N,EM最大迭代次数tmax,NMF的最大迭代次数qmax.

输出：缺失项得到预测的完整QoS矩阵R.

NCNMF＋EM算法的第1步表示产生满足［0, 1］均匀分布的随机矩阵,以初始化QoS基矩阵U和权重矩阵V.第2～7步表示采用最近邻协同过滤方法预测R中的缺失值,然后以预测值填充后的完整矩阵作为X的初始值,详见3.1和3.2节.第10步判断目标函数是否满足收敛条件,假如满足收敛条件则算法结束,其中ε为某个足够小的正数.第13～19步表示采用式（14）所述的乘性法则对因子矩阵U和V进行迭代更新,以实现对R的非负矩阵因子分解,从而得到R的低维逼近矩阵UV,其中16～18步通过对U中的每个元素除以其所在列的所有元素之和,实现对U的规范化操作,以保证矩阵因子分解的唯一性,⊗和⊙分别代表Hardmard乘和除.第21步表示将当前的逼近矩阵UV赋给X,作为下一次EM迭代中的输入参数.经过若干次迭代后, X将趋于收敛,用X中元素取代R中的未观测项将得到包含最终QoS预测值的完整QoS矩阵.

3.1 近邻信息挖掘

假设QoS矩阵R中的Ria＝0,即不存在用户a调用服务i的QoS记录,则可以采用基于服务的最近邻协同过滤法预测Ria.首先采用改进的皮尔逊相关系数计算服务i与其他服务的相似度.皮尔逊相关系数主要用于度量2个变量之间的相关性,因具有易于实现和精度高等特点,被广泛应用于各类推荐系统.服务i和服务r的相似度sim（i,r）可由式（15）所示的改进的皮尔逊相关系数计算得到：

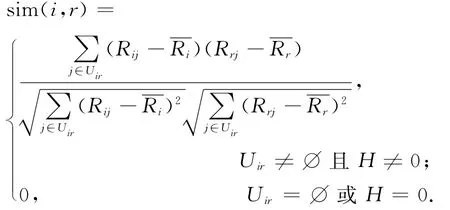
式中：

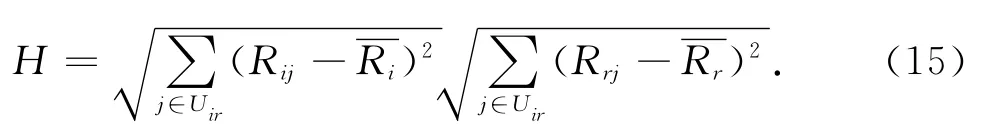
sim（i,r）的取值为［－1,1］,sim（i,r）越大说明两服务越相似.令Ui和Ur分别表示调用过服务i和服务r的用户集,则Uir＝Ui∩Ur表示调用过服务i和服务r的共同用户集.Rij表示用户j观测到的服务i的QoS值,表示Ui中用户观测到的服务i的QoS算术平均值.式（15）与传统的皮尔逊相关系数公式的区别在于考虑了以下2种极端情况.

1）当两服务的共同用户集为Ø时,无法采用传统的皮尔逊相关系数得到有效值.

2）H＝0的情况,采用传统的方法得到的相似度为无穷大,为无效取值.H＝0的情况是可能存在的,比如令服务i和服务r的共同用户为a和b,假如a和b调用服务i时的QoS值相等,并且a和b调用服务r的QoS值相等,此时H＝0.

由于QoS矩阵极度稀疏的,上述2种极端情况很可能出现,式（15）在上述2种极端情况下,令相似度sim（i,r）＝0,以防止出现非法的相似度计算结果.完成服务i与其他所有服务的相似度计算步骤后,令与服务i相似度最高的N个服务组成的集合T（i）称为服务i的Top-N近邻服务集.

3.2 基于服务的最近邻协同过滤

得到服务i的Top-N近邻服务集T（i）后,则可以利用Top-N近邻服务集中的QoS信息对Ria进行协同过滤预测,如下所示：

式中：r为服务i的近邻服务,Rra表示用户a对服务r的QoS体验值.由于QoS矩阵较稀疏,Rra以高概率等于零,在该情况下计算得到的预测值不准确.为了解决该问题,可以在协同过滤预测前采用服务的算术平均值填充近邻集中的缺失值.由于相似度可取负值,采用式（16）计算得到的QoS预测值也可能为负值,而现实中的服务QoS值是非负的,本文采用服务的算术平均值取代这部分负值.

通过以上所述的基于服务的最近邻协同过滤法,原始QoS矩阵中的缺失项将得到较准确的预测值.采用该预测值对原始QoS矩阵进行填充可得完整的QoS矩阵,该完整矩阵将作为NCNMF-EM算法中模型参数X的初始估计值.

4 算法复杂度分析

NCNMF＋EM算法的时间复杂度主要包括近邻信息挖掘、Top-N最近邻协同过滤计算和QoS预测模型参数EM估计3个部分.在实际系统中,通常可以采用离线方式计算服务之间的相似度,并存储Top-N近邻集信息,因此服务近邻信息可以采用定期更新的方式,无需在线计算.本文只考虑Top-N最近邻协同过滤计算和模型参数EM估计2个部分的在线计算时间复杂度.假设QoS矩阵R是n×m矩阵,且共有W个待预测项,EM迭代次数为tmax, NMF算法的最大迭代次数为qmax,特征因子个数为k.Top-N最近邻协同过滤计算的时间复杂度为O（NW）；对R进行一次NMF操作的时间复杂度为O（qmaxkmn）,由于模型参数的EM估计共包含tmax次NMF,复杂度为O（tmaxqmaxkmn）.综上可知, NCNMF＋EM算法的总时间复杂度为O（NW＋tmaxqmaxkmn））.由于W≤mn且N、tmax、qmax和k均为常量,随着QoS矩阵规模mn的增大,NCNMF＋EM算法的运行时间呈线性增长,具有较高的有效性,可以适用于大规模的QoS预测问题.

5 实验分析

采用网络上真实的QoS数据集 WSDREAM［4］对NCNMF＋EM算法的预测准确度和时间性能进行实验评估,研究算法中的Top-N、EM迭代次数tmax、NMF算法迭代次数qmax和特征因子个数k等参数对预测准确度的影响.WS-DREAM数据集记录了30多个不同国家的339个用户调用73个国家的5 825个Web服务的QoS信息.由于该数据集目前只包含响应时间和吞吐量2个QoS属性的信息,实验仅采用响应时间和吞吐量QoS数据对算法进行评估.为了便于分析,从数据集中分别获取了300×3000的响应时间QoS矩阵和300× 3000的吞吐量QoS矩阵.实验环境如下：Intel Core2 Quad 2.50 GHz CPU,4 GB RAM,操作系统为Windows XP,算法实现工具为Matlab 7.1.

5.1 准确度评估

平均绝对误差（MAE）是推荐系统中评价预测精度最常用的度量标准,反映了系统预测值与实际值的平均绝对偏差［21］.MAE的定义如下：

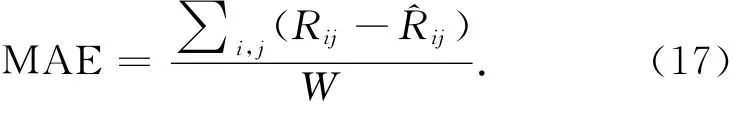
式中：W为QoS矩阵中的待预测项数,Rij为用户j体验到的服务i的QoS实际值,为算法的QoS预测值.在实际应用中,不同QoS属性的取值范围不同,如Web服务的响应时间通常取0～20 s,吞吐量通常取0～1 000 kbit／s［12］,因此采用归一化平均绝对误差（NMAE）对算法的QoS预测准确度进行度量,NMAE越小表示算法的预测准确度越高.NMAE的定义如下：

为了验证NCNMF＋EM算法的QoS预测准确度,与Zheng等［9,19］提出的其他算法进行对比.在该实验中,将QoS数据集分为5个不相交的300× 600矩阵,采用5折交叉验证的思想,分别对这5个 QoS矩阵进行预测.最后取5次实验的NAME均值作为实验结果,以降低数据集误差对算法的影响.在实际应用中,QoS矩阵通常是极度稀疏的,因此在每次实验中,都通过随机移除QoS矩阵中的若干项,得到不同矩阵密度的稀疏QoS矩阵.算法的目标是对这些移除项的QoS进行预测,利用这些移除项的原有值对预测结果的准确度进行评估.在该实验中,QoS矩阵的矩阵密度以0.01为步长从0.04递增到0.13,研究算法在不同矩阵密度下的预测准确度.

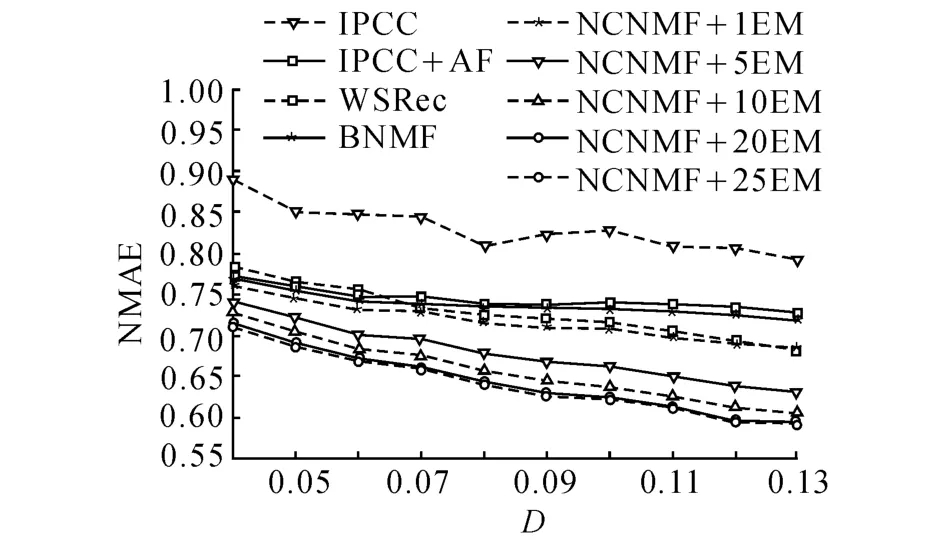
图1 不同矩阵密度下的响应时间预测结果对比Fig.1 Prediction performance comparison on response time w.r.t.density of matrix

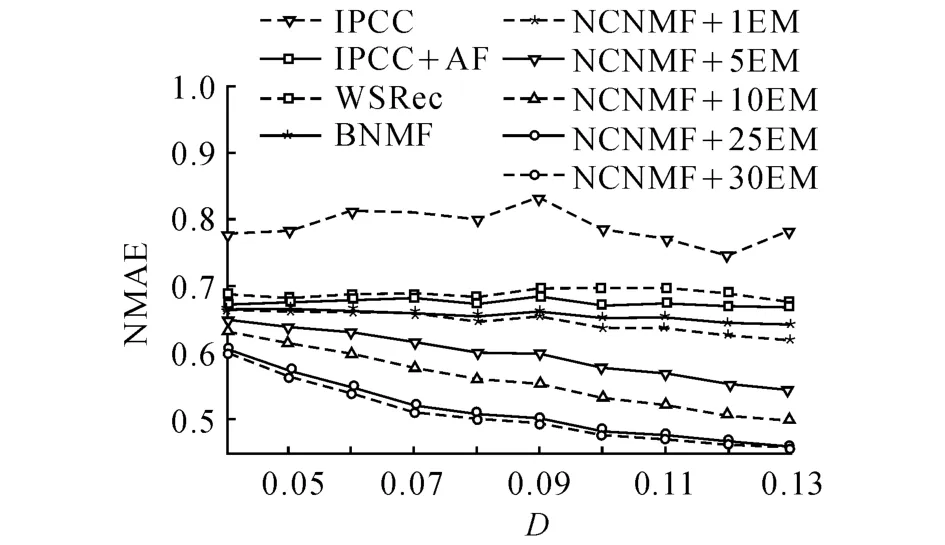
图2 不同矩阵密度下的吞吐量预测结果对比Fig.2 Prediction performance comparison on throughput w.r.t.the density of matrix

图1、2分别给出不同算法在不同矩阵密度D下的响应时间预测结果和吞吐量预测结果.图中, IPCC表示传统的基于服务的协同过滤算法,参数Top-N取10.IPCC＋AF表示采用3.1、3.2节所述的改进的基于服务协同过滤算法,参数Top-N取10.WSRec为文献［9］提出的混合协同过滤算法,参数Top-N和λ分别取文献所述的最优值10和0.2.BNMF（Basic NMF）表示文献［19］提出的基本NMF算法,BNMF直接采用式（14）对稀疏QoS矩阵进行因子分解拟合,未考虑QoS矩阵的稀疏性,也未引入QoS矩阵中的近邻信息,BNMF中的参数特征因子个数取10,迭代次数取100.NCNMF＋EM表示本文提出的结合近邻信息的NMF算法,算法的参数Top-N取10,NMF算法迭代次数qmax取100,特征因子个数k取10.图中,NCNMF＋1EM表示EM迭代次数tmax为1,NCNMF＋5EM表示EM迭代次数tmax为5,以此类推.

由图1、2表明,随着QoS矩阵密度的增大,所有算法的NMAE值都呈下降趋势,即算法的预测准确度呈上升趋势.这是由于QoS信息越丰富,越有利于近邻关系和隐含特征的挖掘,从而提升算法的预测准确度.从图1、2可以发现,NCNMF＋EM只需1次EM迭代,对响应时间和吞吐量的预测准确度普遍优于其他几种算法；当EM迭代次数增大时,算法的预测准确度得到大幅提升.从图1、2可以发现,随着EM迭代次数的增加,NCNMF＋EM算法对响应时间和吞吐量的预测准确度的提升幅度逐渐缩小,并分别于20次和25次左右迭代后收敛到最优值.从图1、2的对比可以发现,WSRec对响应时间的预测准确度较高,且随着矩阵密度的增大准确度提升明显,但是对吞吐量的预测准确度不理想,并且准确度没有随矩阵密度的增大而呈现明显的增长趋势.这可能是由于不同用户体验到的Web服务的响应时间相较于吞吐量而言更稳定,因此近邻信息对于响应时间的预测贡献率较大,对于吞吐量的预测贡献率较小.NCNMF＋EM算法对于2种QoS的预测准确率都较高,表明本文提出的结合近邻信息和隐含特征信息的方法可以更好地通用于不同类型的QoS属性值预测.

5.2 有效性实验

通过对比NCNMF＋EM与其他算法的运行时间t,以评估NCNMF＋EM的时间性能.在本实验中,用户数固定为300,服务数n以100为步长从100递增到1 000,以获取不同规模的用户-服务QoS矩阵,研究算法在不同矩阵规模下的时间性能.所有算法的参数设置与5.1节相同,由于响应时间和吞吐量的预测时间相当,采用响应时间QoS矩阵作为本次实验数据集,矩阵密度取0.1.从图3可以发现,随着矩阵规模的增大,所有算法的运行时间都相应增长,其中BNMF算法的增长幅度最小,效率最高；WSRec的增长幅度最大,效率最低；NCNMF＋EM与IPCC和IPCC＋AF的运行时间相当,均随着矩阵规模的增大呈线性增长,有效性较高,因此可以应用于大规模的QoS预测问题.从图3可以发现,NCNMF＋EM随着EM迭代次数的增加,运行时间没有大幅增加,而是线性增长.结合图1、2可知,NCNMF＋EM通过牺牲部分时间性能,可以显著提升QoS预测的准确度,在实际应用中须在算法效率和算法预测准确度之间进行权衡.

图3 不同矩阵规模下的算法时间性能对比Fig.3 Time performance comparison w.r.t.matrix scale

5.3 收敛性实验

图4 NCNMF＋EM和BNMF的响应时间预测收敛结果对比Fig.4 Convergence comparison between NCNMF＋EM and BNMF for response time prediction

图5 NCNMF＋EM和BNMF的吞吐量预测收敛结果对比Fig.5 Convergence comparison between NCNMF＋EM and BNMF for throughput prediction

该实验对NCNMF＋EM与BNMF的收敛性能进行对比.实验数据分别采用300×600的响应时间和吞吐量QoS矩阵.EM迭代次数取1,特征因子数均取10,QoS矩阵密度为0.05.图4、5表明,NCNMF＋EM的收敛速度和最终收敛值都明显优于BNMF,这主要是由于前者在NMF算法中引入了近邻信息,指导了NMF算法的优化方向,因此可以较快地收敛到最优值.从图4、5可以发现,NCNMF＋EM算法在响应时间和吞吐量的预测中,均在迭代100次左右后收敛,因此在其他实验中,NCNMF＋EM算法中的NMF迭代次数qmax均设为100.

5.4 Top-N对算法准确度的影响

本实验中,将Top-N以3为步长从3递增到30,研究Top-N对NCNMF＋EM预测准确度的影响.算法参数tmax取1,qmax取100,k取10,结果取10次独立运行的平均值.图6、7表明,当Top-N小于某个阈值时,增大Top-N可以提高算法的预测准确度,但超过该阈值时,增加Top-N会降低算法的预测准确度.原因是当Top-N较小时,增大Top-N有利于挖掘出更多的近邻信息,从而提高算法的预测准确度；另一方面,由于QoS矩阵的稀疏度较高造成服务的共同用户数较少,因此与目标服务相似的近邻服务数是有限的,此时若Top-N较高,则将在协同过滤预测中引入大量不相似服务的QoS信息,因此导致预测准确度下降.在实际应用中,可以通过设定相似度阈值,使得超过该阈值的服务被认定为近邻服务,以此动态地确定合理的Top-N.从图6、7可以发现,响应时间和吞吐量的最佳Top-N分别为18和12,表明在预测响应时间时,近邻服务数相对较多.该结果进一步验证了5.1节的猜测,即不同用户体验到的Web服务的响应时间相较于吞吐量而言更稳定.

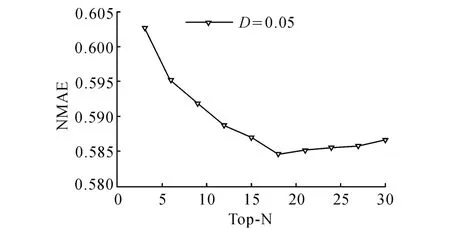
图6 Top-N对响应时间预测准确度的影响Fig.6 Impact of Top-N on response time prediction

图7 Top-N对吞吐量预测准确度的影响Fig.7 Impact of Top-N on throughput prediction

5.5 特征因子数对算法准确度的影响

在该实验中,特征因子数k以3为步长从3递增到30,研究NCNMF＋EM在取不同k时的预测准确度.算法的参数EM迭代次数tmax取1,Top-N取10, NMF迭代次数qmax取100,QoS矩阵密度为0.05.

如图8、9所示分别为NCNMF＋EM在取不同特征因子数时的响应时间和吞吐量预测结果,结果为运行10次的平均值.由图8、9表明,当k较小时,随着k的增加,算法的预测准确度明显上升；当k超过某个阈值时,随着k的增加会导致预测准确度下降.原因是当k过小时,从QoS矩阵中挖掘的隐含特征过少,此时的因子模型难以较好地拟合原始QoS矩阵,导致预测准确度较低；当k过大时,会造成模型的过拟合问题,从而导致算法准确度下降.一般k取满足k≪mn／（m＋n）的正整数,在实际应用中,可以根据实际问题选择若干个k值进行实验验证,以确定最优的k值.

图8 特征因子数k对响应时间预测准确度的影响Fig.8 Impact of k on response time prediction

图9 特征因子数k对吞吐量预测准确度的影响Fig.9 Impact of k on throughput prediction

6 结 语

本文提出采用低维线性模型对QoS观测数据进行拟合,将QoS预测问题转化为稀疏QoS矩阵下的模型参数EM估计问题,提出一种结合近邻信息的非负矩阵分解算法NCNMF＋EM对该问题进行求解.该算法通过挖掘QoS矩阵中的近邻信息和隐含特征信息,可以实现对服务QoS的准确预测.理论分析和实验结果表明,NCNMF＋EM算法的准确度和效率较高,实现简单,可以适用于大规模的不同类型QoS的预测问题.

本文采用的QoS数据集来源于对网络上真实服务的运行监控,因此是客观可信的.在实际应用中,通常还存在来源于服务供应商和用户反馈的不可信QoS数据.下一步将研究不可信QoS数据的滤除方法,以提高在不可信QoS数据条件下对服务QoS的预测准确度.

［1］SU K,MA L,GUO X,et al.An efficient discrete invasive weed optimization algorithm for web services selection［J］.Journal of Software,2014,9（3）：709- 715.

［2］MOSER O,ROSENBERG F,DUSTDAR S.Domain-specific service selection for composite services［J］.IEEE Trans.on Software Engineering,2012,38（4）：828- 842.

［3］SU K,MA L,GUO X,et al.An efficient parameter adaptive genetic algorithm for service selection with endto-end QoS constraints［J］.Journal of Computational Information Systems,2014,10（2）：581- 588.

［4］ZHENG Z,ZHANG Y,LYU R M.Distributed QoS evaluation for real-world web services［C］//IEEE International Conference on Web Services.Miami：IEEE, 2010：83- 90.

［5］YU T,ZHANG Y,LIN K.Efficient algorithms for web services selection with end-to-end QoS constraints［J］.ACM Transactions on the Web,2007,1（1）：1- 26.

［6］XIAO R.Constructing a novel QoS aggregated model based on KBPP［J］.Communications in Computer and Information Science,2010,107（3）：117- 126.

［7］ALRIFAI M,RISSE T.Combining global optimization with local selection for efficient QoS-aware service composition［C］//Proceeding of the 18th International Conference on World Wide Web.New York：［s.n.］,2009：881- 882.

［8］SHAO L,ZHANG J,WEI Y,et al.Personalized QoS prediction for web service via collaborative filtering［C］//IEEE International Conference on Web Services.Salt Lake City：IEEE,2007：439- 446.

［9］ZHENG Z,MA H,LYU R M,et al.WSRec：a collaborative filtering based web service recommender system［C］//IEEE International Conference on Web Services.Los Angeles：IEEE,2009：437- 444.

［10］刘志中,王志坚,周晓峰,等.基于事例推理的Web服务QoS动态预测研究［J］.计算机科学,2011, 38（2）：119- 121.

LIU Zhi-zhong,WANG Zhi-jian,ZHOU Xiao-feng,et al.Dynamic prediction method for web service QoS based on case-based reasoning［J］.Computer Science, 2011,38（2）：119- 121.

［11］张莉,张斌,黄利萍,等.基于服务调用特征模式的个性化Web服务QoS预测方法［J］.计算机研究与发展, 2013,50（5）：1070- 1071.

ZHANG Li,ZHANG Bin,HUANG Li-ping,et al.A personalized web service quality prediction approach based on invoked feature model［J］.Journal of Computer Research and Development,2013,50（5）：1070- 1071.

［12］ZHENG Z,MA H,LYU R M,et al.Collaborative web service QoS prediction via neighborhood integrated Matrix factorization［J］.IEEE Transactions on Services Computing,2013,6（3）：289- 299.

［13］ZHANG Y,ZHENG Z,LYU R M.WSPred：a timeaware personalized QoS prediction framework for web services［C］//IEEE International Symposium on Software Reliability Engineering.Hiroshima：IEEE,2011：210- 219.

［14］彭飞,邓浩江,刘磊.面向个性化服务推荐的QoS动态预测模型［J］.西安电子科技大学学报：自然科学版, 2013,40（4）：207- 213.

PENG Fei,DENG Hao-jiang,LIU Lei.QoS-aware temporal prediction model for personalized service recommendation［J］.Journal of Xidian University,2013, 40（4）：207- 213.

［15］ZHANG S,WANG W,FORD J,et al.Learning from incomplete ratings using non-negative matrix factorization［C］//6th SIAM Conference on Data Mining.Seoul：［s.n.］,2006：548- 552.

［16］SALAKHUTDINOV R,MNIH A.Probabilistic matrix factorization［C］//Proceeding of Advances in Neural Information Processing Systems.Denver：［s.n.］, 2007：1257- 1264.

［17］ZHANG S,WANG W,FORD J,et al.Using singular value decomposition approximation for collaborative filtering［C］//Proceeding of the 7th IEEE International Conference on E-Commerce Technology.Munich：IEEE,2005：1- 8.

［18］SREBRO N,JAAKKOLA T.Weighted low rank approximation［C］//Proceeding of the 20th International Conference on Machine Learning.Washington：［s.n.］,2003.

［19］LEE D D,SEUNG H S.Learning the parts of objects by non-negative matrix factorization［J］.Nature, 1999,401（6755）：788- 791.

［20］LEE D D,SEUNG H S.Algorithms for non-negative matrix factorization［C］//Proceeding of Advances in Neural Information Processing Systems.Denver：［s.n.］,2000：556- 562.

［21］HU R,PU P.Enhancing collaborative filtering systems with personality information［C］//Proceeding of The 5th ACM Conference on Recommender Systems.New York：［s.n.］,2011：197- 204.

Non-negative matrix factorization model for Web service QoS prediction

SU Kai1,2,MA Liang-li2,SUN Yu-fei2,GUO Xiao-ming2
（1.Department of Equipment Economics and Management,Naval University of Engineering,Wuhan 430033,China）（2.Department of Computer Engineering,Naval University of Engineering,Wuhan 430033,China）

An effective Web service QoS prediction approach was presented by utilizing the neighbor information and latent feature information of the observed QoS data.A matrix factor model for service QoS prediction was presented.Then an expectation-maximization（EM）estimation scenario was designed to learn the model based on the available QoS data.A neighbor information combined non-negative matrix factorization algorithm NCNMF＋EM was proposed to implement the scenario.The approach fully utilizes the information of the observed data,and can achieve high prediction accuracy.Experimental results demonstrate that the approach achieves better prediction accuracy than other state-of-the-art approaches.The computational time of the algorithm is linear with the scale of QoS matrix,which indicates that the approach is applicable to large scale QoS prediction problem.

Web service；service selection；QoS prediction；matrix factor model；non-negative matrix factorization；expectation-maximization estimation

10.3785／j.issn.1008-973X.2015.07.022

TP 393

A

1008- 973X（2015）07- 1358- 09

2014- 05- 22. 浙江大学学报(工学版)网址：www.journals.zju.edu.cn／eng

总装预研基金资助项目（9140A27040413JB11407）；国家自然科学基金资助项目（61170217）.

苏凯（1987－）,男,博士,助理研究员,从事服务计算的研究.ORCID：E-mail：keppelsue＠163.com