非机动车影响下的区域交通信号控制优化

邢冰　韩印　徐辉

摘要：我国大中城市区域交通存在严重的机非冲突干扰，本文考虑了非机动车对交叉口以及路段的机动车阻滞干扰，以区域路网机动车总延误最小化为目标，通过折减交叉口通行能力，优化相邻交叉口相位差，建立了非机动车影响下的区域交通控制优化模型，算法的求解采用了传统的遗传算法。通过对上海市五角场环形区域路网分析表明，本文所提出模型进行优化后，区域路网机动车总延误减少了18.81%，有效提高了区域道路网络的运行效率。

关键词：区域信号控制；阻滞干扰；车均延误；非机动车影响

中图分类号：S 773.6；U 491.5+1文献标识码：A文章编号：1001-005X（2015）01-0084-04

Regional Traffic Control Optimization Influenced

by Nonpowerdriven Vehicles

Xing Bing1，Han Yin1*，Xu Hui2

（1.School of Business，University of Shanghai for Science and Technology，Shanghai 200093；

2.Suzhou Municipal Engineering Design Institute Co.，Ltd，Suzhou 215125，Jiangsu Province）

Abstract：Traditional interference problems between vehicles and nondriven vehicles exist in the regional traffic control.The block interferences of nonpowerdriven vehicles on signalized intersections and links were considered.As the optimal index，the total delay was accepted by the model，capacity reduction and phase optimization was analyzed，which built the optimal model.Genetic algorithm was employed to solve the model.Taking Wujiaochang of Shanghai as an example，it is certificated that the total delay decreases by 18.81%，which indicated that the model could effectively improve the efficiency of the regional road network.

Keywords： regional signal control；block interference；average vehicle delay；nonpowerdriven vehicle influence

收稿日期：2014-08-31

基金項目：国家自然科学基金资助项目（51008196）；上海市一流学科项目（S1201YLXK）；上海高校青年教师培养资助计划（slg12009）；同济大学道路与交通工程教育部重点实验室开放基金课题（K201303）

第一作者简介：邢冰，硕士研究生。研究方向：智能交通、交通控制。

*通讯作者：韩印，博士，教授。研究方向：智能交通系统、交通控制与仿真技术研究。Email：hanyin2000@126.com

引文格式：邢冰，韩 印，徐辉.非机动车影响下的区域交通信号控制优化[J].森林工程，2015，31（1）：84-87.以机动车和非机动车为主体的混合交通条件是中国城市道路显著特征之一。从路段方面来讲，机动车道与非机动车道无隔离实施时，非机动车对机动车速影响较大；从交叉口方面来讲，机动车与非机动车在同一平面运行，非机动车易侵占机动车道，导致机动车速大大降低。针对以上混合交通流特性，本文考虑非机动车影响因素，对区域交通信号控制进行优化。

国外学者最早开始研究区域交通控制问题。Robertson提出的TRANSYT系统是一种离线定周期的区域交通信号控制系统优化程序，但模型只是针对静态交通流，不能体现动态交通流特性[1]。Allsop和Gartner阐述了区域交通控制的机理，以及交通信号控制对均衡交通流和车流行程时间有较大影响[2-3]。Yang等提出一个用以确定饱和交通状态下路网交通分配和信号配时关系的双层规划模型，但模型仅将绿信比作为优化参数[4]。

国内学者刘灿齐通过对以交通均衡分配为基础的双层数学规划模型进行改进，构造了区域交通协调控制模型，但是并未对模型的有效性进行验证[5]。李润梅等以饱和交通网络为研究对象，建立了动态交通分配和信号控制一体化的双层模型[6]。徐建闽等采用交通协调两层控制方法进行建模，但模型中没有区分低饱和和过饱和状态[7]。刘芹等以区域交叉口总排队车数与区域总输出车辆数为性能指标，考虑排队车数、相位差和有效绿灯时间，构建了适合各种交通状态的控制模型[8]。张良智以用户均衡理论为基础，考虑了交通状态划分，引入区域通行度算子，但是模型未考虑混合交通的影响[9]。关于混合交通的信号控制研究，主要集中在行人以及非机动车与机动车信号协调方面。李娜分析了非线控路段和线控路段上行人过街信号与交叉口信号协调以及效益评价问题[10]。郑长江系统研究了行人过街信号与交叉口信号联动控制方案[11]。陈小红通过分析慢行交通短距离出行特性的影响，建立了周期、绿信以及相位差优化模型[12]。但模型中未能充分地体现慢行交通特点，以及慢行交通对路网其他交通的影响情况。

综上所述，本文考虑非机动车影响下区域交叉口通行能力的改变以及路段机动车运行延误的影响，建立了区域信号控制优化模型，以此来有效协调区域路网机动车流和非机动车流的有效运行。

1非机动车影响下区域信号控制分析

1.1路段干扰

非机动车对路网机动车的的阻滞干扰是指非机动车占用机动车道阻挡了机动车的行驶，迫使机动车减速行驶，造成延误[13]。本节采用交通流波动理论分析非机动车对路段机动车流延误Tl的影响。由于非机动车占用机动车道，导致机动车队头车减速停驶，跟驰车流发生聚集和消散，因此机动车流会经历一个从疏散到集结再到疏散的过程。设交通流变动分界线将沿交通流运行方向分割成两段，qa、qb、va、vb、ka、kb分别是前后两段交通流量、速度以及密度，从而得到交通波的移速度ρ：

第1期邢冰等：非机动车影响下的区域交通信号控制优化

森林工程第31卷

ρ=（vaka-vbkb）ka-kb。（1）

集结时间tlm中，受阻机动车数增长率δlm与机动车流密度km、集散波速ρlm以及非机动车平均速度v′有关：

qlmax=tlm·δlm=tlm·km（v′-ρlm）。（2）

qlt=δlm（tlm+tle）。（3）

机动车流集结过程中，以微变化时间段t内的受阻车数q（t）以及每车延误时间为基础，得到微变化时间段内的延误时间Tlm，与最大受阻车数qlmax、机动车速v、进而得出机动车流集结过程的延误时间Tlm。同理得到机动车流疏散时间tle内的延误时间Tle：

Tlm=q（t）·（t-v′tv）=qlmax·ttl1（t-v′tv）。（4）

Tlm=qlmax·tlm（1-v′v）/2。（5）

Tle=qlmax·tle（1-v′v/2。（6）

1.2交叉口延误

信号交叉口基本理论中机动车交叉口延误时间Tpn的分析，分为正常相位延误Tpon、随机延误和过饱和延误Tprn，主要与非机动车车速v′、车头空距L′、直行和左转流量q′sl、q′ll以及机动车直左右及相位流量qsl、qll、qrl、qpl有关：

Tpon=Tn（1-λpn）22（1-qpl/Spn）。（7）

Tprn=Tn4[（qplCpn-1）+（qplCpn-1）2+4qplCp2n·Tn]。（8）

通常情况下，当机动车出现可接受间隙时，非机动车会抢先穿越交叉口，造成交叉口延误时间的增加。非机动车影响下机动车通行能力Cpn的减少是增加交叉口延误的重要原因之一，主要与交叉口的饱和流率Spn、信号周期Tn、绿信比λpn有关。本文基于交叉口机非冲突特征，考虑机动车路段饱和流量sl变化，以左转机动车和直行非机动车冲突为主，通过非机动车通过交叉口时间占用相位绿灯时间的比重进行折减，得到折减系数fL：

Cpn=sl·λpn·fL=sl·λpn·qllqpl（1-L′·q′sl1/Tnv′·λpn·Tn）。（9）

2非机动车影响下区域交通控制优化

2.1模型的建立

本文提出的模型主要针对区域信号控制中周期、绿信比以及相位差参数进行优化。首先，针对周期和绿信比的优化，基于左转机动车和直行非机动车冲突对交叉口通行能力进行折减，以交叉口机动车流总延误最小为目标函数，建立区域交通信号控制优化模型如下：

F（T，λ，θ）=min∑l∑n∑pqplTn4[（qplCpn-1）2+4qplCp2n·Tn]l∈L，n∈N。（10）

绿信比λmax、λmin，周期Tmin、Tmin以及相位差θn，n-1、θn-1，n的约束条件如公式（11）～公式（13）所示。其中，L、N分别为区域路网路段以及交叉口集合。

λmin≤λ≤λmax。（11）

Tmin≤T≤Tmax。（12）

θn，n-1+θn-1，n=T。（13）

其次，进行相位差的优化。相位差的优化不仅力求区域路网车辆延误时间最低化，还需要考虑非机动车对路段机动车的干扰影响。低饱和交通状态下，相位差为车流在路段上的平均行驶时间，不随信号周期的变化而变化；近饱和交通状态下，相位差的优化需要考虑交叉口之间的车辆排队长度与拥挤程度[14-16]。当机动车流驶离上游交叉口后，依据路段受到非机动车阻滞干扰引起的延误时间，对区域路网相邻交叉口相位差进行优化，主要与相邻交叉口间距ln-1，n、车辆长度lcar、消散速度ρ以及排队车数q有关[17]，如下：

θn-1，n=ln-1，nv-lcarqv-lcarqρ+qlt·tlm（1-v′v）/2。（14）

2.2求解算法

遗传算法（Genetic Algorithm，GA）是一种求解问题的高度并行性全局搜索算法，它能够自适应地控制搜索过程以求得最优解，快速实现适者生存、优胜劣汰遗传，在诸多领域应用广泛。因此本研究采用遗传算法对上述模型进行求解，主要包括以下几个步骤：

（1）首先初始进化代数令gen=0，确定遗传算法的参数设置，如种群規模P、最大进化代数M、交叉概率pc、变异概率pm。

（2）设定二进制染色体位数，对模型中决策变量F（T，λ，θ）进行二进制编码，随机设定初始群Y作为初始信号配时方案。

（3）将路段流量值代入目标函数中，得到个体对应的适应度函数值，按个体适应度进行排序。当k>M时，算法结束，转入5，最终得到适应度最大个体对应的周期、绿信比方案即为最终的信号设置方案；否则令k=k+1，转入4进行最优个体选择。

（4）按照轮盘赌方法进行选择，按照比例将个体适应度转化为个体选中概率，筛选出第k代种群，按照概率对种群中个体进行交叉、变异，得到新一代种群，转入3，求得新一轮适应度函数值。

（5）若滿足k>M，终止运算，输出最大适应度的个体作为最优解，得到最优控制方案；若k≤K，则k=k+1转入3重新求得个体对应的适应度函数值。

3案例分析

如图1所示，本文以上海市杨浦区五角场区域为例，主要包括8个交叉口，5条主干道，4条次干道。其中，交叉口3、5、6、7为四相位信号控制，其他交叉口为三相位信号控制。各交叉口早高峰的现状交通信号控制方案和不同交通流数据，分别见表1和表2。

图1五角场路网简图

Fig.1 Wujiaochang road network

表1现状交通控制s

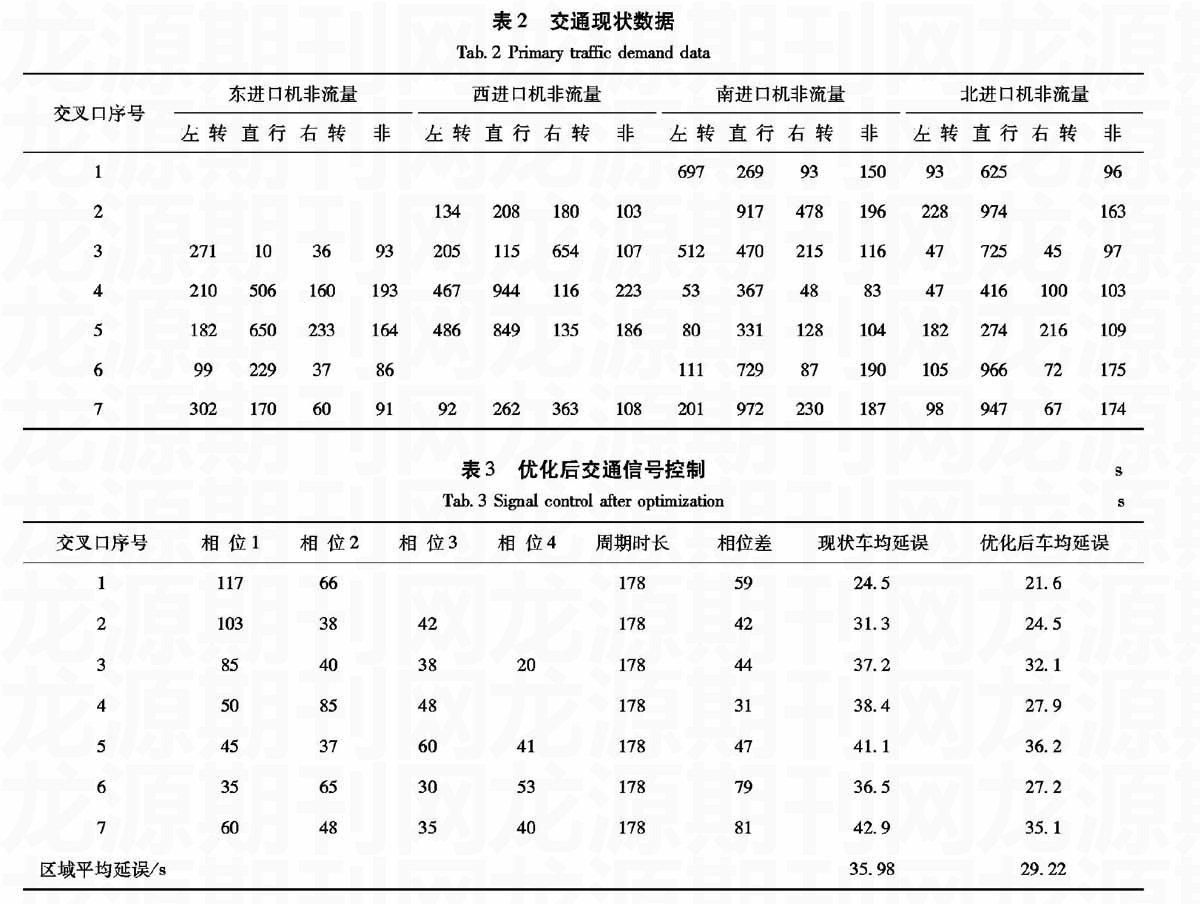
通过MATLAB编程设置各个参数：Tmax=220，Tmin=50；λmax=0.8，λmin=0.2；v′=45，v′=1.0；L′=0.5；sl=1 800，s′l=600；pc=0.95，pm=0.05，P=20，M=150。由于交叉口8的非机动车通过地下通道完成过街，本模型暂不考虑交叉口8。运用本文的模型对路网各交叉口信号参数进行优化，见表3，得到交叉口公共周期时长为178 s。采用VISSIM仿真对优化前后效果进行评价，可以看出，现状路网车辆平均延误为36.98 s，路网总延误为231.2 h。优化后交叉口车辆平均延误为29.22 s，路网总延误为186.4 h。

表2交通现状数据

Tab.2 Primary traffic demand data

交叉口序号东进口机非流量左转直行右转非西进口机非流量左转直行右转非南进口机非流量左转直行右转非北进口机非流量左转直行右转非1〖10〗6972699315093625962〖6〗13420818010391747819622897416332711036932051156541075124702151164772545974210506160193467944116223533674883474161001035182650233164486849135186803311281041822742161096992293786〖10〗111729871901059667217573021706091922623631082019722301879894767174

表3优化后交通信号控制s

Tab.3 Signal control after optimizations

交叉口序号相位1相位2相位3相位4周期时长相位差现状车均延误优化后车均延误111766〖6〗1785924.521.6210338421784231.324.53854038201784437.232.145085481783138.427.95453760411784741.136.26356530531787936.527.27604835401788142.935.1区域平均延误/s〖8〗35.9829.22

分析可知，区域路网现状车均延误为36.98 s，通过本文模型对路网交通控制方案的改善，路网机动车辆平均延误降为29.22 s，总延误降低了18.81%。所以考虑非机动车影响条件，能够有效降低区域路网车辆整体延误时间，证明了本文模型的适用性和有效性。

4结束语

本文考虑非机动车对机动车流在交叉口以及路段阻滞干扰，以区域路网机动车辆交叉口总延误为优化目标，对区域交通控制优化模型进行了分析，并采用传统的遗传算法进行求解。案例表明，通过本研究优化方案，路网机动车辆平均延误为29.22 s，与现状车均延误36.98 s相比，总延误降低了18.81%。本研究模型能够有效降低区域路网机动车流总延误时间，进一步验证了本文优化模型有效性。但是，本文未考虑行人流特征对机动车流的运行影响因素，机动车与非机动车其他转向的冲突也不全面，有待深入研究。

【参考文献】

[1]Robertson D I.TRANSYT：a traffic network study tool[R].Transport and Road Research Laboratory，Crowthrone，1969.

[2]Allsop R E.Some possibilities for using traffic control to influence trip distribution and route choice[A].In：Buckley D J，eds.The Proceeding of the Sixth International Symposium on Transportation and Traffic Theory[C].New York：Elsevier；1974：345-374.

[3]Gartner N H.Area traffic control and network equilibrium[A].In：Florian MA，eds.Traffic Equilibrium Methods[M].New York：Springer，1976：274-297.