关于环评中公众参与问卷调查样本数量的探讨

韩明爽 李钢 唐菲 王珏

摘要：针对目前环评公众参与问卷调查工作中存在的调查数量随意性、调查结果可信程度的不确定性等问题，通过对现阶段典型公众参与调查问卷结构进行分析、对问卷调查结果样本分布特性等问题进行讨论，将统计学中关于样本数量确定的方法引入环评公众参与问卷调查样本数量的确定中，并给出了相应的确定步骤及需要注意的问题。以期有助于提高环评公众参与问卷调查结果的科学性和可信性。

关键词：

环评；公众参与；问卷调查；样本数量

DOI： 10.14068/j.ceia.2015.06.018

中图分类号：X828文献标识码：A文章编号：2095-6444（2015）06-0079-05

问卷調查作为环评公众参与（以下简称“公参”）调查中的一种重要方式，在日常环评工作中被广泛采用。但长期以来对于其需要调查的数量以及调查结果的可信程度等问题，始终没有明确的说法。现行的《环境影响评价公众参与暂行办法》关于公参问卷的调查，也只是要求：“问卷的发放范围应当与建设项目的影响范围相一致；问卷的发放数量应当根据建设项目的具体情况，综合考虑环境影响的范围和程度、社会关注程度、组织公众参与所需要的人力和物力资源以及其他相关因素确定”。新颁布的《环境保护公众参与办法》要求：调查问卷“调查的人数及其范围应当综合考虑相关事项或者活动的环境影响范围和程度、社会关注程度、组织公众参与所需要的人力和物力资源等因素”。对于一个具体的项目，调查问卷到底该做多少份以及项目的支持率到底需要达到多少方可接受、调查结果到底能在多大程度上反映公众的意见等问题，各方均无明确的说法。

本文尝试应用统计学相关理论，探讨环评公参中的调查问卷数量以及调查结果的可信程度、误差范围等问题，期望能够有助于环评公参工作的日益公正、科学和可信。

1统计学相关理论

1.1样本数量的确定

根据统计学理论，对于总体置信水平为1-α、绝对误差为d的样本分布（如图1及公式（1）），在重置抽样或无限总体抽样条件下，样本数量可按公式（2）进行确定；对于有限总体，样本数量需在公式（2）计算的基础上，进行必要的修正，具体修正方法见公式（3）。

上述公式，E为总体均值；σ2为总体方差；为样本均值；d为估计误差；1-α为置信水平（也称置信度）；zα/2为上分位数；N为总体数量；n为无限总体需调查的样本数量；n′为有限总体需调查的样本数量。由上述理论可知，对于具体的总体进行样本分析时，在确定的估计误差、置信水平情况下，只需了解其样本分布，进而获取其样本方差，即可确定所需调查的样本数量。

1.2伯努利分布特点及其样本数量的确定

伯努利分布（The Bernoulli Distribution），又名两点分布或者0-1分布，是一种离散型的概率分布，其特点是只有两种可能的结果，即成功/失败、支持/不支持或者0/1。

若X服从概率为pV的伯努利分布，则记为X～Bern（p），其期望值E（X）=p，方差D2=Var（X）=p（1-p）。由此，根据公式（2）可得出伯努利分布样本数量n的计算公式：

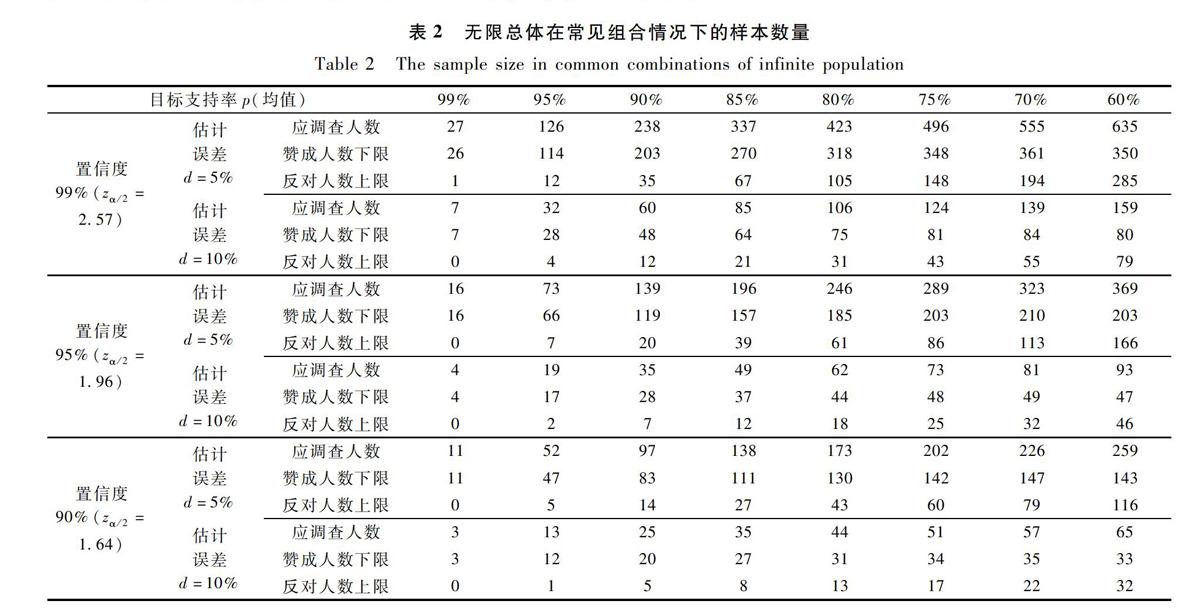
在应用表2进行样本数量的确定时，需要注意以下两点问题：

（1）对于需调查的样本总体数量无法视为无限总体的情况下（一般认为n/N>5%时），还需在表2结果的基础上按公式（3）进行适当修正（修正后的样本数量会略小于修正前的样本数量）。

（2）对于总体数量小于表2（即公式（4）计算出来的样本数量）的调查对象，一般需对总体进行100%的调查，以期达到需要的调查精度。

2.3公参样本调查结果的验证

由2.2节的叙述可知，利用公式（4）进行样本数量的确定时，是首先假定公参调查的期望结果，而后再依据问卷调查的情况验证事先假定结果的准确性。

具体验证的方法是：验证实际调查得到的支持率p′与事先假定目标支持率p之差是否满足假定的估计误差d，即验证|p′-p|≤d是否成立。

（1）如果|p′-p|≤d，则认为样本数量确定中事先假定的条件成立，得出结论：在置信水平为1-α、允许估计误差为d的前提下，公众支持率可以达到p（目标支持率）；

（2）如果|p′-p|>d，则认为事前假定的条件不成立，需要重新假定条件（即降低目标支持率p、调整估计误差d或置信水平1-α）确定样本数量，并补充不足的问卷调查，然后重新验证，直至假定条件成立。

为便于在公参现场调查中及早发现假定条件可能存在的问题，表2中在给出不同目标支持率p（即期望值）、估计误差d和置信水平1-α条件下对应的样本数量时，还给出了与之相对应的赞成人数下限和反对人数上限的数量。在环评公参现场调查中，一旦发现调查人数中反对的人数高于反对人数上限（或支持的人数低于赞成人数下限），即应及时调整假定条件，重新确定样本数量，并按重新确定的样本数量进行公参调查，避免全部现场调查结束后，返回单位再判定假定条件是否成立，出现二次甚至多次现场补做公参的现象。

2.4公参问卷调查样本数量确定推荐的步骤

总结环评公参问卷调查中，样本数量确定的操作步骤：

（1）首先根据项目可能影响到的敏感对象情况，确定公参调查样本总体的数量N（可以是人数或者户数）；

（2）综合考虑项目的特点，当地环境敏感程度、受影响公众情况、环保要求及评价期望值等多方面因素，初步假定公参调查的目标支持率p、估计误差d、置信度1-α等参数；

（3）按照表2或公式（4）确定需调查的公参问卷数量（即样本数量），对于样本总体数量不足以视为无限总体时，还需按照公式（3）进行适当修正；

（4）按照确定的样本数量进行现场问卷调查；

（5）计算问卷调查中得到的实际公众支持率p′，并进行结果验证：

如果|p′-p|≤d，得出结论：在置信水平为1-α、允许估计误差为d的前提下，公众支持率可以达到p（目标支持率）；

如果|p′-p|>d，则假定条件不成立，需要重新进行步骤（2）～（5）的工作 。

3应用举例

为便于理解以上样本数量的确定步骤，此处例举了一个典型的例子。具体如下：

某项目环评中涉及三个居民小区的公参调查，其中A小区共有低矮居民建筑6栋，居民288户、806人，位于项目西南，最近居民建筑距离项目边界约30 m；B小区共有低矮建筑3栋，居民32户、90人，位于项目东侧，最近居民建筑距离项目边界约50 m；C小区共有高层建筑4栋，居民384户、1 075人，位于项目东北，最近居民建筑距离项目边界约120 m。当地主导风向为东北风。

按照2.4节步骤确定调查样本数量，进行公众参与调查，详见表3。

结论置信水平95%，误差范围5%，公众支持率可达到90%置信水平100%，误差范围0，公众支持率可达到88%置信水平90%，误差范围5%，公众支持率可达到85%

注：*B小区样本总体小于需调查的样本数量，因此进行了逐户（逐人）调查；** 此处为考虑第一轮、第二轮两部分调查结果的综合支持率。[HT]

调查中，考虑到A小区距离项目较近且位于项目的下风向，因此为A小区设置了较高的目标，在第一轮假定的目标支持率p=95%，估计误差d=5%，置信水平1-α=99%（希望代表99%民众的意见）。但从第一轮的调查结果看，假定目标不成立，因此需调整目标重新进行第二轮调查（此处将目标降低至支持率p=90%、置信水平1-α=95%）；第二轮调查中，在充分利用第一轮成果基础上，仅补充进行了新假定目标增加的样本数量的调查。

而B小区由于样本总体数量（32户、90人）小于计算得到的需调查样本数量（97户或97人），因此需进行逐户（逐人）调查。

通过上述公参调查最终得出结论：A小区在置信水平为95%（即代表95%民众的意见），误差范围为5%的情况下，公众支持率可达90%；B小区由于进行了逐户（逐人）调查，因此置信水平为100%（即代表100%民众的意见），误差范围为0%，公众支持率可达88%（调查支持率）；C小区在置信水平为90%（即代表90%民众的意见），误差范围为5%的情况下，公众支持率可达85%。

在此案例中，考虑到不同小区与项目的位置关系不同，可能受到的影响相差较大，因此工作中为三个小区假定了不同的目标支持率、置信水平和估计误差，并据此确定各自的调查样本数量，进行问卷调查，得出不同小区对该项目的公众支持率。对于敏感程度不高的项目，也可以不区分小区，将各敏感点视为一个整体统一进行调查。

4结论

本文将统计学中关于样本数量确定的方法引入环评公参问卷调查样本数量的确定，并给出相应的步骤及需注意的问题，通过这种方法将有助于使调查结果更为科学、可行。

参考文献（References）：

[1]国家环保总局. 环境影响评价公众参与暂行办法[Z]. 2006.

[2]环境保护部. 环境保护公众参与办法[Z]. 2015.

[3]张小斐. 统计学（第二版）[M]. 北京： 中國统计出版社， 2013： 125129.

[4]邢文听. 环境影响评价公众参与调查问卷存在问题分析[J]. 环境与可持续发展， 2010（5）：2729.