基于IF-ANP的机场物流园区物流服务供应商选择

陈可嘉, 林月柑

(福州大学经济与管理学院,福建福州350108)

基于IF-ANP的机场物流园区物流服务供应商选择

陈可嘉, 林月柑

(福州大学经济与管理学院,福建福州350108)

构建了机场物流园区物流服务供应商选择指标体系。基于直觉模糊理论,将决策者给出的主观评价信息转化为直觉模糊数,并结合网络分析法,提出了一种多属性群体决策方法,通过实例说明了该方法的有效性。

机场物流园区;供应商选择;直觉模糊;网络分析法;多属性决策

机场物流园区又称航空物流园区,它依托于航空飞行器及机场地面配套物流设施,为多家航空货代、综合物流企业等提供货站、仓库、地勤、航空快递中心、增值服务等物流功能服务,以及提供信息平台、多式联运协调、行政管理、后勤保障等辅助功能服务[1]。机场物流园区的建设促进了航空物流的发展,然而由于资金和技术的限制,如何引入适当的物流服务供应商进行有序竞争、提供高效服务,成为决策者们亟需解决的问题。

物流服务供应商选择是物流与供应链管理中的焦点问题。一方面,由于物流服务供应商选择的复杂性,评价指标之间往往并不独立,很多学者运用网络分析法(Analytic Network Process,ANP)处理评价指标间的相依关系并获得权重。宫俊涛等[2]选择质量、价格、柔性及供应商的声誉等作为评价准则,运用ANP方法构建了物流服务供应商选择的依存、反馈网络。Jharkharia和Shankar[3]认为,ANP方法可使决策者更好地理解物流服务供应商选择中的复杂关系,提高选择的可靠性。王宁和孔德洋[4]在处理汽车行业物流服务供应商选择问题时,分析了汽车物流外包各参与方的角色,利用ANP方法建立了各层指标非线性组合关系的多指标综合评价决策模型。Chen等[5]从服务质量、服务能力、联盟性以及成本4个方面考虑逆向物流服务供应商选择问题,提出基于ANP和熵值法的组合权重确定方法。另一方面,在物流服务供应商选择过程中涉及很多定性指标,应用模糊语言评价供应商是比较合适的。一些学者结合Zadeh教授的模糊理论提出了模糊网络分析法(Fuzzy Analytic Network Process,FANP)。李君和黄绍服[6]构建物流服务供应商选择的ANP网络,利用三角模糊数确定供应商的判断尺度,依据几何平均值方法对多位专家的判断进行综合,在此基础上,运用截集方法求解FANP问题。Nia和Farrokh[7]在模糊环境下将ANP方法与VIKOR方法相结合,提出物流服务供应商选择模型。传统模糊方法在一定程度上解决了决策过程的模糊性,但在实际应用过程中,不能同时表示支持(肯定)、反对(否定)和犹豫(不确定)的状态。1983年,保加利亚的Atanassov教授[8]提出直觉模糊集(Intuitionistic Fuzzy Set,IFS)概念,利用两标度(即隶属度和非隶属度)刻画了支持、反对、犹豫3种状态,这更加符合人们的思考及行为方式。

机场物流园区物流服务供应商选择受到企业客户关系、服务价格、企业软实力、业务能力及信息化程度等因素的影响,这些影响因素之间存在着彼此依赖、反馈等关系。不仅如此,机场物流园区的评审专家在对候选物流服务供应商进行评价时,并非只是做出“支持”和“反对”两种选择,还存在“中立”(“犹豫”)的现象。因此,文中将直觉模糊理论(IF)和网络分析法(ANP)结合起来,发挥两个理论的优势,提出直觉模糊网络分析法(IF-ANP),解决评价指标间带有反馈、依赖关系的直觉模糊多属性群体决策问题,并应用于机场物流园区物流服务供应商选择。

1 基于IF-ANP的多属性群体决策方法

设X是一个非空论域,称A={[x,μA(x), vA(x)]|x∈X}为直觉模糊集,其中μA(x)和vA(x)分别为X中元素x属于A的隶属度和非隶属度,即

μA(x):X→[0,1],x∈X→μA(x)∈[0,1], vA(x):X→[0,1],x∈X→vA(x)∈[0,1],且满足0≤μA(x)+vA(x)≤1,x∈X。πA(x)=1-μA(x)-vA(x),x∈X,表示X中元素x属于A的犹豫度或不确定度。

假设有m家备选的物流服务供应商,A={A1, A2,…,Am}。用以评价供应商的属性(即评价指标)有n个,F={F1,F2,…,Fn}。ω={ω1,ω2,…,ωn}是属性的权重向量。

1.1 确定决策者权重

表1为语言变量对应的直觉模糊数。

表1 语言变量对应的直觉模糊数Tab.1 Intuitionistic fuzzy numbers corresponding the linguistic variab les

假定组成决策小组的决策者有p个,决策者的重要性用语言变量表示,根据表1将语言变量转化为直觉模糊数[9]。设DMk=(μk,vk,πk)表示第k个决策者的权重,用下列公式将其转化为实数:

1.2 构建决策矩阵

根据各个评价指标,p个决策者分别用语言变量评价备选物流服务供应商。根据表1,将语言变量转化为直觉模糊数,构建第k个决策者的决策矩阵R(k)=)m×n。在群体决策中,所有个体决策得出的决策矩阵必须进行集结,得到最终综合所有决策者意见的决策矩阵。文中利用直觉模糊加权平均算子进行集结,得到矩阵R=(rij)m×n,其中:

1.3 确定决策属性权重

考虑到属性之间具有相互依存关系,文中基于直觉模糊理论,应用ANP方法计算各个属性的权重[10]。

1.3.1 建立网络结构 ANP典型结构描述由两大部分组成,即控制层和网络层。元素组之间具有3种关系,分别为内部依存、外部依存和反馈关系,其网络结构如图1所示。

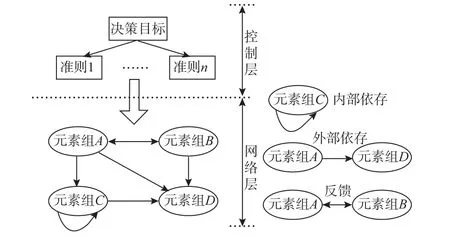
图1 ANP网络结构Fig.1 Network structure of ANP

1.3.2 构建判断矩阵 设ANP网络结构中的网络层有n个存在相互影响关系的元素组,记为C1, C2,…,Cn,在元素组Ci中含有元素Ci1,Ci2,…,Cim。在这些元素组中,某些元素如果受到组内元素的影响,就存在内部依存关系;如果受到其他元素组中元素的影响,就存在外部依存关系;如果受到其他元素组中元素的影响,同时又影响这一元素组中的元素,就存在反馈关系。例如,若元素组Cj中元素Cjk受到元素组Ci中元素的影响,则以元素Cjk为准则,将元素组Ci中的元素根据对Cjk影响程度的大小用语言变量表示。根据表1将专家意见用相应的直觉模糊数表示,建立判断矩阵B=(bxy)m×n,其中bxy= (μxy,vxy,πxy)。

1.3.3 构建未权重化的超矩阵 根据判断矩阵,可以得到在元素Cjk下元素组Ci的第h个元素的重要性程度:

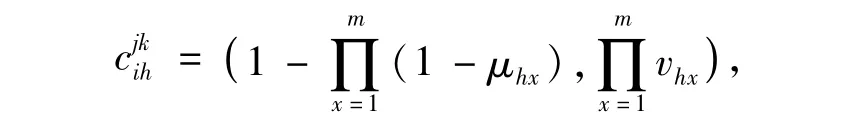
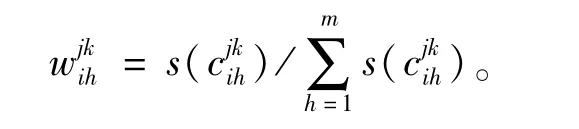
1.3.4 构建权重化的超矩阵 未权重化超矩阵W的分块矩阵Wji是列归一化矩阵,但就整体而言,W并非是列归一化的。因此,还需要在每一元素为次准则条件下进行元素组间的比较,得到加权矩阵

其中,矩阵的第k列表示以Ck(k=1,2,…,n)为次准则,按照各组元素对Ck的重要性进行比较。

利用加权矩阵D对未权重化超矩阵W进行加权处理,即可得到权重化超矩阵¯W,此时权重化超矩阵¯W即为列归一化矩阵。

1.3.5 权重化超矩阵的极限处理 权重化超矩阵¯W表示任意元素组中任一元素对其他元素组中任一元素的直接影响程度的偏好度量。¯W2是二次影响程度的偏好度量,¯Wk是k次影响程度的偏好度量。当k→∞时,就得到了决策者的综合偏好度量。在权重化超矩阵的幂运算过程中,如果幂收敛,那么可以把这个收敛的结果作为综合权重。如果出现周期性,可以取平均作为综合权重。

经过IF-ANP的计算,求得属性的权重向量为ω={ω1,ω2,…,ωn}。

1.4 集结决策信息

在确定决策者权重及决策属性权重之后,通过加权平均算子式(2)将决策矩阵进行集结,得到各备选方案最终的决策信息,每个方案对应一个直觉模糊数。

1.5 方案排序

对于任一直觉模糊数α=(μα,vα),其得分函数为s(α)=μα-vα,精确函数为h(α)=μα+vα。根据直觉模糊数的得分函数和精确函数,可以给出一种直觉模糊数的排序方法[11]。

设α1=(μα1,vα1)和α2=(μα2,vα2)分别为两个直觉模糊数:

1)当s(α1)＜s(α2),则α1小于α2,记为α1＜α2。

2)当s(α1)=s(α2),①若h(α1)=h(α2),则α1等于α2,即μα1=μα2且vα1=vα2,记为α1=α2;②若h(α1)＜h(α2),则α1小于α2,记为α1＜α2;③若h(α1)＞h(α2),则α1大于α2,记为α1＞α2。

2 机场物流园区物流服务供应商选择实例分析

某市机场物流园区通过公开招标的方式,组织3名决策者DM1,DM2,DM3对物流服务供应商进行初步筛选,淘汰了一部分不合格的供应商,剩下5家备选的合格供应商,分别为S1,S2,S3,S4,S5。现根据以上的多属性群体决策方法对这5家供应商进行选择。

2.1 构建指标体系

基于文献[5,12-13]的研究成果,结合机场物流的行业情况,将机场物流园区物流服务供应商选择指标体系分为客户关系、服务价格、企业软实力、业务能力、信息化程度5个方面(见表2)。

2.2 确定决策者权重

根据调查评估,得到3名决策者重要性的语言变量,通过式(1),转化为实数权重,具体结果见表3。

表2 机场物流园区物流服务供应商选择指标体系Tab.2 Logistics service provider selecting index system in the airport logistics park

表3 决策者权重Tab.3 Decision makersweights

2.3 构建决策矩阵

根据式(2),由初始判断矩阵得到集结后的决策矩阵(见表4)。

表4 决策矩阵Tab.4 Decision makersmatrices

2.4 确定决策属性权重

依据指标之间的作用关系,建立如图2所示的机场物流园区物流服务供应商选择的网络结构。

限于篇幅,文中选择其中一个元素为例进行说明。以“准时交货率A1”为准则,比较“客户关系元素组A”中的其他元素对A1的重要性程度。构成的判断矩阵见表5,求得

图2 机场物流园区物流服务供应商选择的网络结构Fig.2 Network structure of logistics service providers in airport logistics park

同理,根据评价指标之间的相互影响关系大小,依次构建其余判断矩阵,并求得归一化权向量,将得到的所有归一化权重向量按顺序进行排序,得到未权重化的超矩阵(见表6)。同时,在每一元素为次准则下元素组进行两两比较,得到加权矩阵(见表7)。

表5 准时交货率下客户关系相关元素的判断矩阵Tab.5 Judgmentmatrices of the customer relationship elements under on-time delivery rate

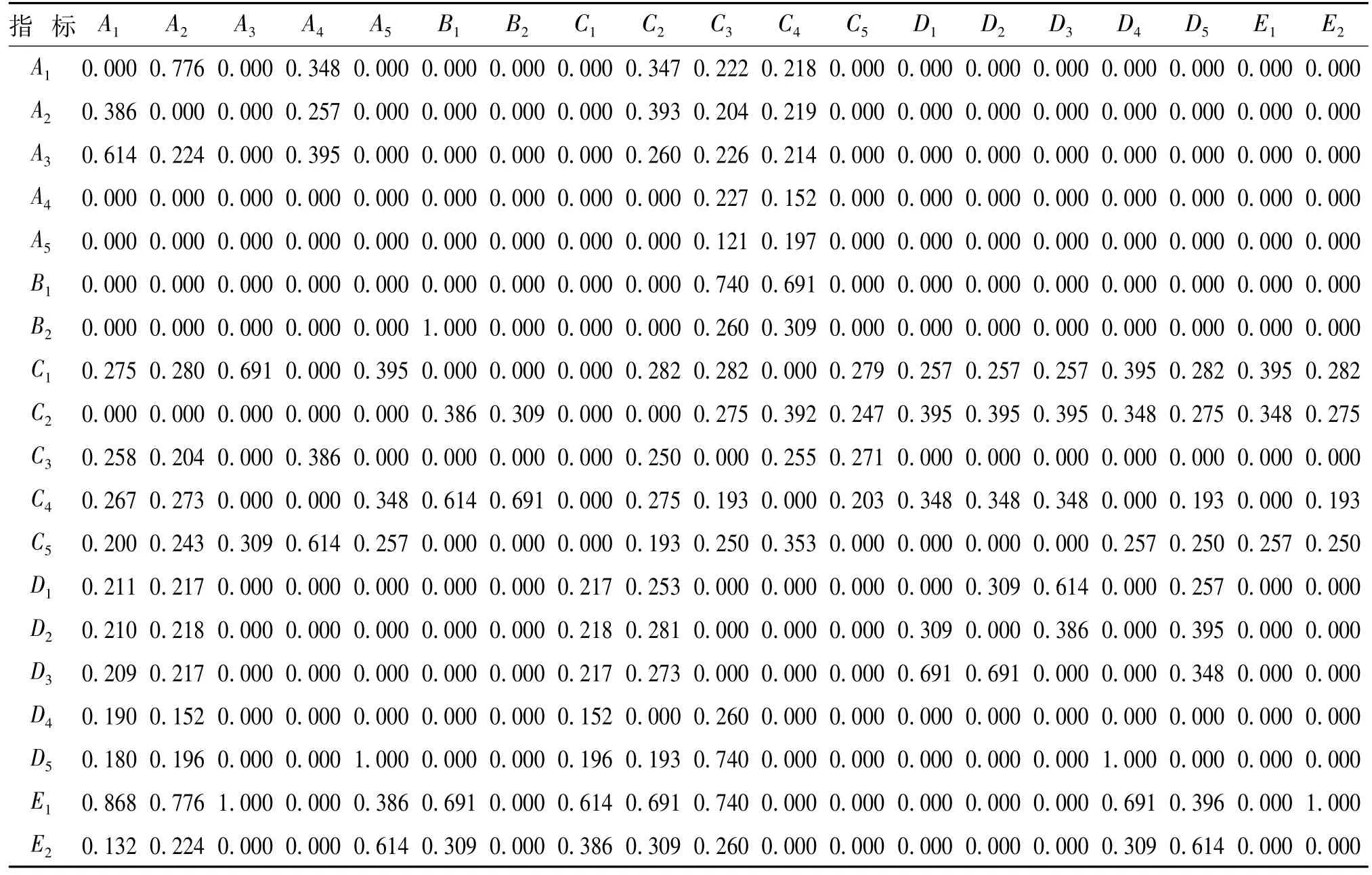
表6 未权重化的超矩阵Tab.6 Unweighted superm atrix

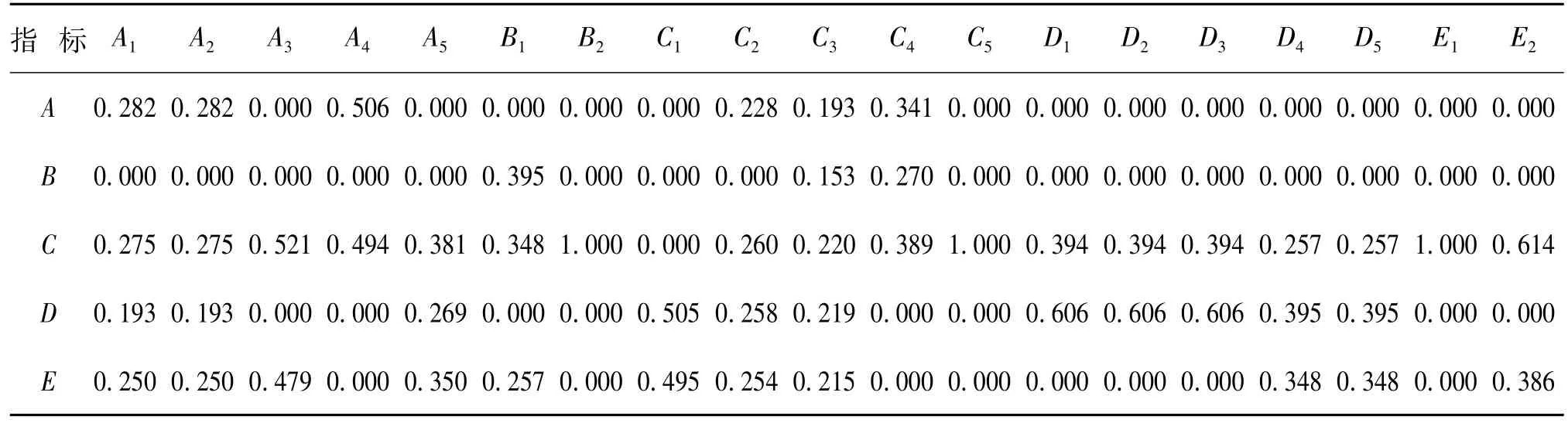
表7 加权矩阵Tab.7 W eighted supermatrix

通过未权重化的超矩阵和加权矩阵相乘,得到权重化的超矩阵。当权重化超矩阵的幂次运算达到14次时即可达到稳定状态,从而得到极限矩阵。在极限矩阵中,任取一列为决策者所给出的各指标的权重值:

2.5 集结决策信息

通过加权平均算子对备选方案的决策信息进行集结,得到5家物流服务供应商的综合评价信息(见表8)。

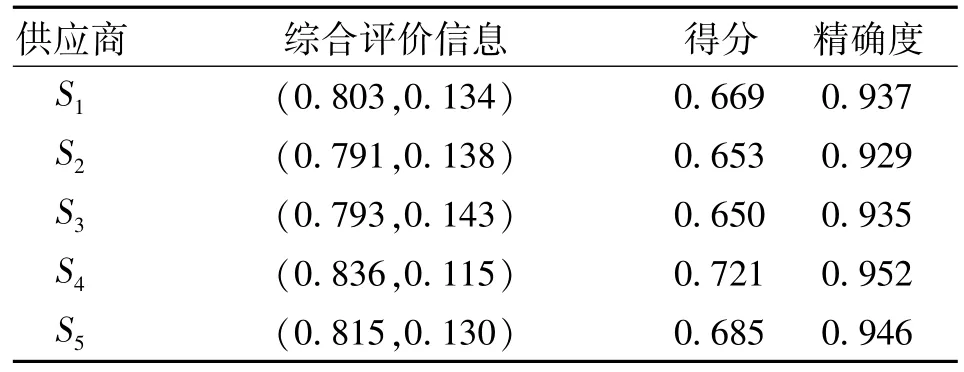
表8 物流服务供应商的综合评价信息Tab.8 Evaluation information of logistics service provides

2.6 方案排序

根据直觉模糊数得分函数和精确函数的定义,由表8的综合评价信息计算得到5家供应商的得分和精确度,同样列于表8中。从而可以对5家物流服务供应商进行排序,即S4≻S5≻S1≻S2≻S3。该排序说明了在这5家物流服务供应商中,S4是最优的,当需要选择多个供应商时,可依据排序进行选取。

3 结 语

机场物流园区通过引入优质的物流服务供应商,既可以保持有利的竞争,避免垄断和低效率,又可以形成一定的规模效益,促进园区的发展。文中构建了机场物流园区物流服务供应商选择的指标体系,充分考虑指标之间的依赖、反馈关系,给出指标体系的网络结构图,并运用直觉模糊数表达决策者的偏好,较好地处理评价过程中的模糊性和不确定状态。实例研究表明,提出的直觉模糊-网络分析法(IF-ANP)在机场物流园区物流服务供应商选择问题中的有效性。

[1]云俊,崔绍先.航空物流园区规划及设施布局研究[J].武汉理工大学学报:社会科学版,2002,15(3):236-239.

YUN Jun,CUI Shaoxian.On air logistics park design and facilities establishment[J].Wuhan University of Technology:Social Science Edition,2002,15(3):236-239.(in Chinese)

[2]宫俊涛,刘波,孙林岩,等.网络分析法(ANP)及其在供应商选择中的应用[J].工业工程,2007,10(2):77-80.

GONG Juntao,LIU Bo,SUN Linyan,et al.Analytic network process and application for supplier selection[J].Industrial Engineering Journal,2007,10(2):77-80.(in Chinese)

[3]Jharkharia S,Shankar R.Selection of logistics service provider:an analytic network process(ANP)approach[J].Omega,2007, 35(3):274-289.

[4]王宁,孔德洋.汽车行业物流服务供应商选择ANP模型[J].工业工程与管理,2009,14(4):72-77.

WANG Ning,KONG Deyang.Analytic network processmodel for selecting logistics service provider of automotive industry[J]. Industrial Engineering and Management,2009,14(4):72-77.(in Chinese)

[5]CHEN K J,YU X K,YANG L X.GI-TOPSIS based on combinational weight determination and its application to selection of reverse logistics service providers[J].The Journal of Grey System,2013,25(3):16-33.

[6]李君,黄绍服.基于模糊网络分析法的供应商评价研究[J].煤矿机械,2009,30(7):219-221.

LIJun,HUANG Shaofu.Supplier assessmentwith fuzzy analytical network process[J].Coal Mine Machinery,2009,30(7):219-221.(in Chinese)

[7]NIA H H,Farrokh M.A vendor selection model based on ANP and VIKOR under fuzzy environment[J].Global Journal of Management Studies and Researches,2014,1(2):62-72.

[8]李登峰.直觉模糊集决策与对策分析方法[M].北京:国防工业出版社,2012.

[9]ZHANG S,LIU S.A GRA-based intuitionistic fuzzy multi-criteria group decision making method for personnel selection[J]. Expert Systemswith Applications,2011,38(9):11401-11405.

[10]孙宏才,田平,王莲芬.网络层次分析法与决策科学[M].北京:国防工业出版社,2011.

[11]XU ZH,Yager R R.Some geometric aggregation operators based on intuitionistic fuzzy sets[J].International Journal of General Systems,2006,35(4):417-433.

[12]王燕,谢蕊蕊.物流外包合作伙伴选择的两阶段混合决策方法——基于DEMATEL-ANP-VIKOR混合决策模型[J].中国流通经济,2012,26(8):30-36.

WANG Yan,XIE Ruirui.The two-stage hybrid decision research of logistics outsouring partners selection:using the DEMATELANP-VIKOR[J].China Business and Market,2012,26(8):30-36.(in Chinese)

[13]索玮岚,樊治平.关联情境下物流服务外包商选择的混合型决策分析方法[J].运筹与管理,2013,22(1):138-146.

SUOWeilan,FAN Zhiping.A hybrid decision analysis method for vendor selection of logistics services outsourcing under correlation context[J].Operations Research and Management Science,2013,22(1):138-146.(in Chinese)

(责任编辑:邢宝妹)

Selection of Logistics Service Providers in Airport Logistics Park Based on the IF-ANP M ethod

CHEN Kejia, LIN Yuegan
(School of Economics and Management,Fuzhou University,Fuzhou 350108,China)

The selection of logistics service providers in the airport logistics park is a typicalmulti-attribute decision making problem.The logistics service provider selection index system in the airport logistics park is built.Based on the intuitionistic fuzzy theory,the decision maker′s subjective evaluation information is converted into the intuitionistic fuzzy numbers.Combined with the analytic network process,a multi-attribute group decision making method is proposed.Finally,an empirical study is conducted to show the effectiveness of the proposed method.

airport logistics park,provider selection,intuitionistic fuzzy,analytic network process,multi-attribute decisionmaking

Email:kjchen@fzu.edu.cn

F 252

A

1671-7147(2015)01-0110-07

2014-09-18;

2014-10-18。

国家自然科学基金委员会与中国民用航空局联合项目(61179061);教育部新世纪优秀人才支持计划项目(NCET-11-0903)。

陈可嘉(1978—),男,福建福州人,教授,工学博士。主要从事管理系统工程等研究。