改进的瑞利阻尼系数计算方法在岸桥结构地震反应分析中的应用*

李哲 王贡献 胡勇 胡吉全

(武汉理工大学 物流工程学院，湖北 武汉430063)

集装箱码头大多处于深海港口，地震频繁、强度大，超大尺寸结构的集装箱起重机(简称岸桥)在地震灾害中最易遭受破坏. 明确岸桥结构地震激励下的反应过程及破坏机理，提高其抗震性能，是当前设计领域高度关注的问题［1］.

现代化港口的岸桥结构巨大，无法对其进行全尺寸试验分析.为了研究岸桥地震反应情况，一些研究机构采用有限元软件进行数值仿真配合缩尺模型振动试验，取得了众多有意义的成果. 其中，阻尼参数对结构动力时程计算结果的影响不可忽略［2］. 但由于没有相应的试验验证，在有限元时程分析中选用哪一种阻尼系数确定方法比较合理，尚没有一个评价指标.文献［3］对1∶50 的岸桥缩尺模型进行振动台地震模拟试验，并采用有限元软件对岸桥结构进行时程分析，得到的试验值与有限元计算结果相近.文献［4］以相似理论为指导，制造出相似比为1∶20的岸桥缩尺模型，在此基础上进行了一系列的有限元仿真分析和振动台试验，取得了理想的结果.但以上研究中都没有对有限元数值计算中阻尼系数的确定方法进行说明，更没有用试验来验证数值分析中阻尼系数的正确性［5-9］.

瑞利阻尼系数对有限元结构地震反应时程分析计算结果有很大影响，采用合理的瑞利阻尼系数计算方法可以使有限元模拟岸桥结构地震反应更加准确.文献［10］总结了不同阻尼系数确定方法，对现有方法进行改进，采用不同阻尼系数对土石坝进行了时域动力分析，并与频域计算结果进行了比较，结果表明:当坝高超过一定高度后，采用结构基频确定瑞利阻尼系数的方法高估了结构的阻尼，导致结构的动力反应偏小;改进后的方法能较好地反映结构的阻尼特性，但是研究对象单一，缺少针对性的试验数据，方法不具有普遍性.文中采用工程上最常用的4 种阻尼系数计算方法和改进的方法，计算得到5 组不同的阻尼系数，将其分别设置在有限元计算程序中，对同一岸桥结构进行时程分析，得到在不同地震激励下不同阻尼系数的结构地震反应，并与振动台地震模拟试验所得的试验值进行比较.

1 阻尼系数计算方法

瑞利阻尼是目前有限元分析中应用最广的，采用瑞利阻尼系数法定义阻尼矩阵C 时，可以通过两个系数α、β 与质量矩阵M 和刚度矩阵K 来表示:

式中α、β 为阻尼系数，可以根据该结构在所研究振动方向上的整体振动对应的第m 阶振型阻尼比ξm、固有频率ωm和第n 阶振型阻尼比ξn、固有频率ωn进行计算:

低阶振型在工程结构的动力反应中起主导作用，例如取前两阶振型频率ω1和ω2、阻尼比ξ1和ξ2，通过计算得出阻尼系数α、β，则其他各阶振型的阻尼比可通过下式求解:

目前，结构动力反应计算中瑞利阻尼系数通常采用下面4 种方法进行计算.

(1)假定瑞利阻尼中质量矩阵和刚度矩阵的贡献相同，则阻尼系数α 和β 可以表示为

由结构的基频ω1得到阻尼系数α 和β.这种阻尼系数的计算方法早在20 世纪70年代已经采用，我国较多工程应用中也采用这种阻尼系数计算方法.

(2)选定对象结构的敏感频率范围为fa～fb，在频率边界ωa、ωb处的阻尼比可用下式表达:

根据上式求出阻尼系数α 和β.

(3)以方法(2)为基础，一些学者对其进行了改进［11］，令

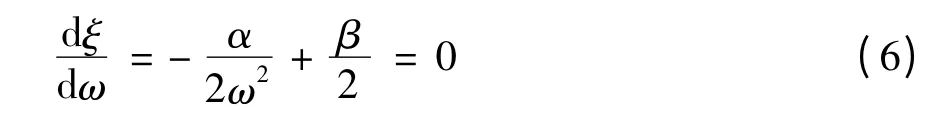
(4)Hudson 等［12］针对方法(1)仅采用基频确定阻尼系数的缺陷，进行了适当的改进，确定了新的瑞利阻尼系数取值方法，用ω1和ω2两个频率来确定α 和β，ω1为结构的基频，ω2=nω1，n 是大于ωe/ω1的奇数，其中ωe为地震波的主频. 此法既考虑了结构频率特性，也考虑了地震动频率特性.

文中根据文献［10］中提出的一种改进瑞利阻尼系数计算方法，采用方法(4)计算频率ω1和ω2，采用方法(3)确定阻尼系数α 和β.这样改进后的方法既考虑到了结构的频率特性和地震动的频谱特性，也不会过多低估或高估结构在ω1和ω2范围内的阻尼，计算得到的阻尼矩阵能够更合理地反映结构的阻尼特性.

2 岸桥结构地震反应

2.1 研究对象与模型

对集装箱岸桥进行地震反应计算分析，讨论在不同瑞利阻尼系数计算方法所得的阻尼系数下岸桥结构地震反应的区别. 集装箱岸桥结构主要由门架结构、前后大梁、前后拉杆等组成，其结构如图1 所示.岸桥由Q345 钢构成，弹性模量为206 GPa，泊松比为0.3，密度为7850 kg/m3.

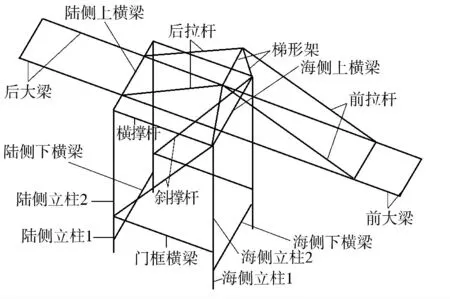
图1 集装箱岸桥结构示意图Fig.1 Structural model of the quayside container crane

采用大型有限元软件ANSYS 对试验岸桥进行有限元建模，模型如图2 所示.模型采用三维beam188单元，前后大梁之间的铰接通过节点自由度耦合模拟，拉杆与上横梁、前大梁之间的铰接通过节点自由度耦合模拟;4个立柱底端与地面刚性连接(自由度全耦合，试验台和相似模型即为此连接方式).以现场试验模型(见图3)为基准，根据结构静动力实验(静力加载试验与模态分析)进行结构的参数识别，对有限元模型进行修正，得到岸桥结构的基准有限元模型.计算过程中在各立柱基底处沿小车运行方向分别输入EL-Centro 波、Taft 波，步长设置为0.02 s.

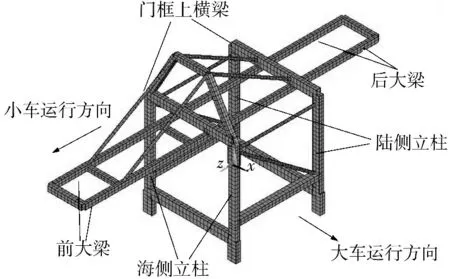
图2 集装箱岸桥有限元模型Fig.2 Finite element model of the container crane

图3 试验现场Fig.3 Test on site

2.2 不同阻尼系数下的岸桥结构地震反应

为了比较不同阻尼系数下的岸桥结构地震反应，采用工程上最常用的4 种瑞利阻尼系数计算方法以及改进的阻尼系数计算方法得到5 组不同的阻尼系数，对同一岸桥结构进行有限元数值时程分析.将5 组不同阻尼系数分别计为R1、R2、R3、R4、R5.通过锤击模态试验测得岸桥结构前8 阶频率［13］，利用QR 分解技术得到传感器位置的初始布置点，按模态置信度(MAC)准则进行传感器优化布置，在岸桥模型的前大梁、后大梁以及门架结构处布设了29个加速度传感器［14］. 试验现场如图3 所示，所测结果如表1 所示，有限元模型计算频率与实测结果及误差见表2.

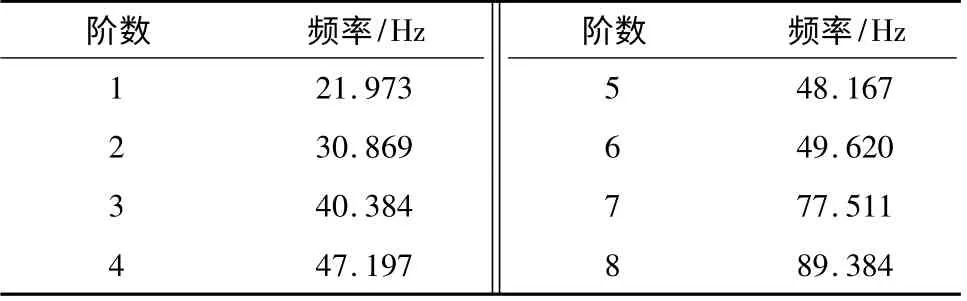
表1 岸桥自振频率Table 1 Frequency of the container crane

表2 模型固有频率计算结果与实测结果Table 2 Calculation and test results of the natural frequency of the model

有限元模型通过静动力实验进行结构的参数识别，但是其计算模态结果与实测结果还是有细微差别［15］，结果有差异的原因包括:①有限元模型通过静力加载试验后进行过细微的简化;②测点传感器布置位置的误差以及传感器本身误差;③锤击实验人员因经验不足产生的操作误差以及锤击产生的非线性问题;④外部环境因素等. 相对误差非常小、振型结果与有限元计算基本一致，说明文中有限元基准模型的精确性得到了保障. 将表中结果代入前文中方法进行计算，得到5 组阻尼系数，如表3 所示.其中，EL-Centro 波、Taft 波的主频分别为1.818 和2.272Hz，按相似比(见表4)换算成27.27 和34.1Hz，根据结构基频21.973 Hz 计算得出两种地震波下n均为3，所以阻尼系数R5 相等.

表3 阻尼系数Table 3 Damping coefficients

在有限元计算程序中设置好阻尼系数，取测点S6 进行观察(测量点的选取是基于现实情况下岸桥结构的危险易发点)，测点位置布置如图4 所示.

图4 测量点布置图Fig.4 Measurement nodes of the model

在EL-Centro 波、Taft 波下测点S6 的加速度时程曲线(有限元计算值与试验值对比)如图5、6 所示，其中试验值是通过振动台模型试验获取的结果.

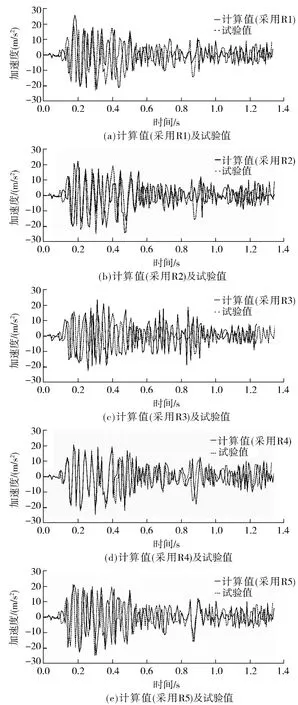
图5 EL-Gentro 波下考察点S6 的加速度时程曲线Fig.5 Acceleration time-history curves of S6 with EL-Gentro

观察图5、6 可知，在EL-Centro 波下，采用阻尼系数R4与R5时，有限元时程计算值与试验值最为接近;在Taft 波下，采用阻尼系数R3 与R5 时，有限元时程计算与试验值最为接近.由此可见，在不同地震波激励下，同一岸桥结构时程分析时采用同一种阻尼系数计算方法(工程中常用的4 种方法)得到的阻尼系数不一定与试验值吻合，而采用改进的方法得到的阻尼系数使岸桥在不同地震波下时程分析结果与试验值相近.

图6 Taft 波下考察点S6 的加速度时程曲线Fig.6 Acceleration time-history curves of S6 with Taft

2.3 振动台模型试验

采用振动台地震模拟试验来验证数值计算的结果.试验现场如图3 所示，岸桥结构相似缩尺模型的相似系数见表4.振动台主要参数如下:振动台台面长1500 mm，台面宽1 500 mm，水平方向最大加速度为±50 m/s2，竖直方向最大加速度为±30 m/s2，水平方向最大位移为±200 mm，竖直方向最大位移为±100 mm，水平方向最大速度为0.8 m/s，竖直方向最大速度为0.8 m/s，最大承载力为2 t，频率范围为0.1 ～100 Hz.

表4 岸桥缩尺模型的相似关系Table 4 Similarity relation of the scale model

在模型上取测量点S12，考察其在EL-Centro 波和Taft 波下，采用R4 和R5 对应方法所得阻尼系数的有限元时程计算以及试验加速度时程曲线;取测量点S14，考察其在EL-Centro 波和Taft 波下，采用阻尼系数R3 和R5 对应方法所得阻尼系数的有限元时程计算以及试验加速度时程曲线.

图7 EL-Gentro 波下考察点S12 的加速度时程曲线Fig.7 Acceleration time-history curves of S12 with EL-Gentro

图8 Taft 波下考察点S12 的加速度时程曲线Fig.8 Acceleration time-history curves of S12 with Taft

观察图7、8 可以看出，在EL-Centro 波下，岸桥结构有限元时程分析采用阻尼系数R4 和R5 时，两次有限元计算结果与试验值接近;在Taft 波下，继续采用阻尼系数R4 和R5，发现R4 情况下时程分析与试验值偏差较大，而R5 情况下时程分析与试验值接近.观察图9、10 可以看出，在EL-Centro 波下，岸桥结构有限元时程分析采用阻尼系数R3 和R5时，发现R3 情况下时程分析与试验值偏差较大，而R5 情况下时程分析与试验值接近;在Taft 波下，继续采用阻尼系数R3 和R5，两次数值计算结果与试验值接近.综合上述结果，可以说明结构在某一地震波下适用的阻尼系数计算方法(工程上常用的4 种)不一定适用于其他地震波，而改进的方法能在不同地震波下计算得到合适的阻尼系数.

图9 EL-Gentro 波下考察点S14 的加速度时程曲线Fig.9 Acceleration time-history curves of S14 with EL-Gentro

图10 Taft 波下考察点S14 的加速度时程曲线Fig.10 Acceleration time-history curves of S14 with Taft

为了进一步说明该方法具有一般性，继续采用Kobe 地震波进行时程计算以及试验分析. Kobe 地震波主频为5Hz，按相似比换算成75Hz，计算得n=5，阻尼系数R5，α =0.623，β =6.01 ×10-4，与ELCentro 地震波和Taft 地震波下阻尼系数有差异. 选取考察点S12，分析其在3 种地震波下位移时程计算结果与试验结果.

由图11 可知，考察点位移时程曲线与试验结果曲线吻合度很高. 在Kobe 地震波下，阻尼系数R5的值发生了变化，在此情况下，计算值与实测值仍然保持较好的吻合，这说明文中的阻尼系数计算方法具有一般性，既考虑了结构的频率特性又考虑了地震动的频谱特性，不会过多低估或高估结构在ω1和ω2范围内的阻尼，这样得到的阻尼矩阵能够更合理地反映结构的阻尼特性.

观察图4 -11，R5 阻尼系数下有限元数值计算和试验结果误差较小，在不同地震载荷下考察点加速度曲线形状、极值大小以及对应时间都比较近似.误差在一定许可范围内，试验结果总体与数值计算结果相近，说明时程分析中采用文中方法计算得到的阻尼系数R5 所得的结果是可靠的，同时也使得相似缩尺模型的有效性得到了进一步验证.

3 结语

图11 3 种地震波下考察点S12 的位移时程曲线Fig.11 Displacement time-history curves of S12 under three kinds of seismic waves

文中比较了目前常用的几种确定瑞利阻尼系数的方法，提出了适合岸桥结构的阻尼系数计算方法.该计算方法考虑了结构的频率特性和地震动的频谱特性.文中还将该方法应用到岸桥结构地震反应动力时程分析中，研究发现:在不同地震波激励下，同一岸桥结构时程分析时采用同一种阻尼系数计算方法(工程上常用)得到的阻尼系数不一定与试验值吻合;同样，不同型号的岸桥结构采用同一种阻尼系数计算方法得到的阻尼系数与试验值之间存在较大误差.改进的阻尼系数计算方法得到的阻尼系数能使不同岸桥结构在EL-Centro 地震波和Taft 地震波、Kobe 地震波下时程分析结果与试验值相近. 由于文中无法开展大量的结构试验，使得试验结果不具有普遍性，后期将会对不同结构的岸桥起重机进行相似模型设计及振动台模型试验，以寻求一种在岸桥起重机范围内通用的瑞利阻尼系数计算方法.

［1］李哲，胡吉全，王东.地震载荷作用下岸桥结构单参数畸变相似模型研究［J］. 振动与冲击，2014，33(20):174-179.Li Zhe，Hu Ji-quan，Wang Dong.Distortion model of container cranes subjected to seismic load［J］.Journal of Vibration and Shock，2014，33(20):174-179.

［2］楼梦麟，张静. 大跨度拱桥地震反应分析中阻尼模型的讨论［J］.振动与冲击，2009，28(5):23-28.Lou Meng-lin，Zhang Jing.Discussion on damping models for seismic response analysis of long-span bridge ［J］.Journal of Vibration and Shock，2009，28(5):23-28.

［3］Jin Y L，Li Z G.Theoretical design and experimental verification of a 1/50 scale model of a quayside container crane［J］. Proceedings of the Institution of Mechanical Engineers，Part C:Journal of Mechanical Engineering Science，2012，226(6):1644-1662.

［4］Jacobs L D，Reginald DesRoches，Roberto T Leon.Seismic behavior of a Jumbo container crane including uplift［J］.Earthquake Spectra，2011，27(3):745-773.

［5］王春健，陈官峰，卿华.涡轮叶片模态实测阻尼比的有限元应用［J］.航空动力学报，2012，27 (2):260-264.Wang Chun-jian，Cheng Guan-feng，Qing Hua.Application of damping ratio for turbine blades by modal testing on finite element analysis load［J］. Journal of Aerospace Power，2012，27(2)，260-264.

［6］侯兴民，孔令召，陈建立.地基阻尼比测试的一种计算方法［J］.岩土力学，2010，31(9):2995-2999.Hou Xing-min，Kong Ling-zhao，Chen Jian-li. A subsoil damping ratio testing and data processing method ［J］.Rock and Soil Mechanics，2010，31(9):2995-2999.

［7］李小珍，雷虎军，朱艳. 车-轨- 桥动力系统中Rayleigh 阻尼参数分析［J］. 振动与冲击，2013，32(21):52-58.Li Xiao-zhen，Lei Hu-jun，Zhu Yan. Analysis of Rayleigh damping parameters in a dynamic system of vehicle-trackbridge ［J］. Journal of Vibration and Shock，2013，32(21):52-58.

［8］周国伟，张志强，李爱群，等. 混合结构时程分析中的阻尼比计算研究［J］.振动与冲击，2012，31(16):117-122.Zhou Guo-wei，Zhang Zhi-qiang，Li Ai-qun，et al. Damping ratio of composite structures used in time-history analysis［J］.Journal of Vibration and Shock，2012，31(16):117-122.

［9］战吉艳，陈国兴，杨伟林，等. 苏州第四纪沉积土动剪切模量比和阻尼比试验研究［J］. 岩土工程学报，2012，34(3):559-566.Zhan Ji-yan，Chen Guo-xing，Yang Wei-lin. Experimental study on dynamic shear modulus ratio and damping ratio of Suzhou quaternary sedimentary soil［J］.Chinese Journal of Geotechnical Engineering，2012，34(3):559-566.

［10］邹德高，徐斌，孔宪京. 瑞利阻尼系数确定方法对高土石坝地震反应的影响研究［J］.岩土力学，2011，32(3):797-803.Zou Gao-de，Xu Bin，Kong Xian-jing. Study of influence of different methods for calculating Rayleigh damping coefficient on high earth-rock dam seismic response［J］.Rock and Soil Mechanics，2011，32(3):797-803.

［11］Yoshida N，Kobayashi S，Suetomi I，et al. Equivalent linear method considering frequency dependent characteristics of stiffness and damping［J］. Soil Dynamics and Earthquake Engineering，2002，22(3):205-222.

［12］Hudson M，Idriss I M，Beikae M. User manual for QUAD-4m:a computer program to evaluate the seismic response of soil structures using finite element procedures and incorporating a compliant base［D］. Berkeley:University of California，1994.

［13］陈舟，颜全胜，胡俊亮，等.人群-桥梁耦合振动研究及参数分析［J］.华南理工大学学报:自然科学学版，2014，42(5):75-83.Chen Zhou，Yan Quan-sheng，Hu Jun-liang，et al. Coupling vibration investigation and parameter analysis of crowd-bridge system［J］.Journal of South China University of Technology:Natural Science Edition，2014，42(5):75-83.

［14］滑广军，吴运新.混凝土泵车臂架结构健康监测传感器优化布置［J］.华南理工大学学报:自然科学学版，2012，40(12):41-46.Hua Guang-jun，Wu Yun-xin. Optimal sensor placement for health monitoring of boom structure of concrete pump truck［J］.Journal of South China University of Technology:Natural Science Edition，2012，40(12):41-46.

［15］刘鑫，刘伟庆，王曙光，等.加固加层隔震结构阻尼比特性的振动台试验［J］.东南大学学报:自然科学版，2012，42(6):1151-1156.Liu Xin，Liu Wei-qing，Wan Shu-guang，et al. Shaking table test of damping ratio of strengthening-adding-story isolation structures［J］.Journal of Southeast University:Natural Science Edition，2012，42(6):1151-1156.