基于频域直方图和HVS的彩色图像质量评价算法

秦 川，李小飞

(长江大学工程技术学院，湖北荆州434020)

彩色数字图像早已成为主流媒体形式，图像处理和传输过程中会引入失真或噪声，因此图像质量评价［1］(IQA)成为关键。目前已有许多图像质量评价方法:均方差(MSE)、峰值信噪比(PSNR)、PSNR-HVS-M［2］、结构相似性质量因子(SSIM)［3］、MS-SSIM［4］、通用质量指标(UQI)等。其中最简单且应用最广泛的IQA是MSE，然而MSE和PSNR均不能处理许多特殊情况，并且评价结果不够准确，对于某些失真的敏感度较低。

主流图像质量评价算法均基于图像的空间域进行质量分析，而对于某些失真，空间域差异较小，但是频率域差异明显，本文对图像频率域进行直方图分析。已有的部分图像质量评价算法从不同角度考虑了人类视觉系统(HVS)的影响［5］，而本文从一个新的角度结合HVS特性，对彩色图像质量进行评价，提出了HHBQA(基于直方图和HVS的图像质量评价)质量评价算法。HHBQA包括2个创新步骤:1)基于图像频率域做直方图计算分析;2)利用HVS特征对评价结果进行权重分配。本文对彩色图像的质量评价结果与实际感官高度一致，具有较好的准确性和敏感性。

1 相关知识介绍

1．1 YUV 变换

典型的彩色图像颜色用RGB 3个通道表示，通常一个像素颜色占24 bit数据:红、绿、蓝分别占8 bit。彩色图像分为压缩和非压缩两种，通常彩色图像压缩先将RGB转换为YUV颜色空间。

JPEG和JPEG2000采用YUV转换，其正向转换和逆向转换分别如式(1)和式(2)所示

YUV转换将原颜色空间去相关，并删除部分信息从而使熵下降。而该部分删除信息无法恢复，因此该转换过程不可逆。JPEG2000中采用近似可逆分量变换(RCT)，表示为

因图像压缩并非本文关注点，所以本文采用RCT变换，即RGB转换YUV(RCT)过程中无数据丢失。

1．2 傅里叶变换

傅里叶变换将信号转换成若干三角波形叠加，其变换公式如下

其中，正弦曲线为ωk=2πk/N，相位为φk，正弦波形系数为ck。

数字图像可由二维离散信号f(x，y)表示，因此，大小为M×N的二维图像离散傅里叶变换为

其中

二维傅里叶变化可扩展为

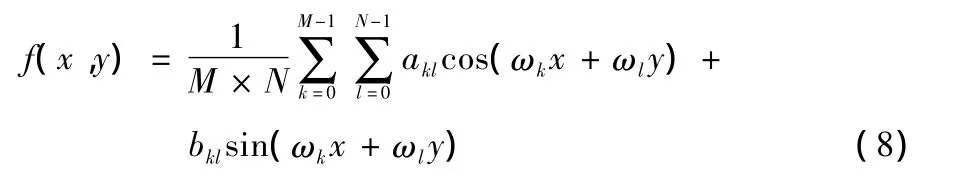
其中

傅里叶系数是复数，其大小可由幅度和相位计算得到，假设FT系数为真实空间的一个向量，其大小和相位角分别如文献［6-7］定义

1．3 图像直方图

已有研究大多针对图像空间域做直方图分析，如灰度直方图。本文基于图像频率域做直方图分析。利用傅里叶变换将二维图像转换为频率域，所得图像频率分布图即为图像梯度分布图，频率表现了相邻像素点间的变化剧烈程度，而傅里叶幅度值表示相应频率占所有频率的比重大小。

图1a为Lena图像(512 × 512，24 bit/pixel)，图1b为Lena图像经JPEG压缩后的失真图像，2幅图片PSNR值均为27.67 dB。分别对图1中原图像Lena和失真图像Lena的R、G、B 3个通道做傅里叶变换并得到相应的傅里叶系数，对所得傅里叶系数的幅度值做三维立体直方图分析。结果如图2所示，图中三维立体直方图均通过MATLAB mesh()函数绘制得到。

图1 Lena原图像和经JPEG压缩过的失真图像

由图2可见，部分情况下利用PSNR值(空间域算法)无法评价图像质量差异(图中PSNR值均为27.67 dB)。而通过图像的频率域直方图，可简单清晰地辨别图像差异(图像频率域直方图差异明显)。

2 HHBQA彩色图像质量评价算法

HHBQA算法如图3所示，由4部分组成:1)进行可逆YUV变换;2)对YUV每个通道的傅里叶变换结果进行直方图计算;3)基于直方图计算每个通道质量评价(HQA);4)基于HVS(人眼视觉特性)权重计算图像总质量评价。

HHBQA算法流程:

1)利用RCT变换，将RGB彩色图像转换成YUV颜色空间。

2)首先将YUV 3个通道分别进行二维离散傅里叶变换，将空间域转换为频率域，计算得到YUV各通道的傅里叶系数。

其次利用YUV各通道的傅里叶系数，计算各频率的幅度值直方图:原图像(H(YFT)，H(UFT)，H(VFT))，失真图像

3)计算得到各通道的直方图质量评价结果(YHQA，UHQA，VHQA)。

HQA由下式计算得到

ΔTCfactor表示直方图差异因子，以Y通道为例，其差异如下计算得到

图2 Lena图像和失真Lena图像的傅里叶幅度直方图

式中:Δ表示原图像和失真图像直方图间的差值。而原图像和失真图像的总差异(ΔTC)可由所有Δ相加得到

ΔTCfactor如下计算得到

ΔTCfactor区间为0～1，0为最严重失真，1为无失真。ΔTCmax为直方图差异是2×M×N的极限情况。

HD值(直方图失真)由相关经典公式表示

如同ΔTCfactor，HD最优值为1，表示无失真;0为最差值。

综上可知，当ΔTCfactor=1且HD=1时，HQA值为最优值，等于1;当ΔTC=ΔTCmax时，HQA值为最差值，等于0。将以上算法应用于其他直方图(H(UFT)和H(VFT))，可得YHQA、UHQA和 VHQA。

4)考虑 HVS［8］(人眼视觉特性)特点，对 HQA 结果(YHQA，UHQA，VHQA)进行权重分配。该步骤为本算法另一个创新点。

人类视网膜有2种光受体:视杆和视锥。视杆负责低亮度时的视力，无颜色识别功能，且几乎无空间知觉。而视锥高亮度时活跃，并负责颜色感知和空间感知。眼球有近7百万视锥和1亿2千万视杆。视杆负责亮度感知，而视锥负责颜色感知。由此可推导眼睛感知过程中，视杆和视锥的权重计算如下

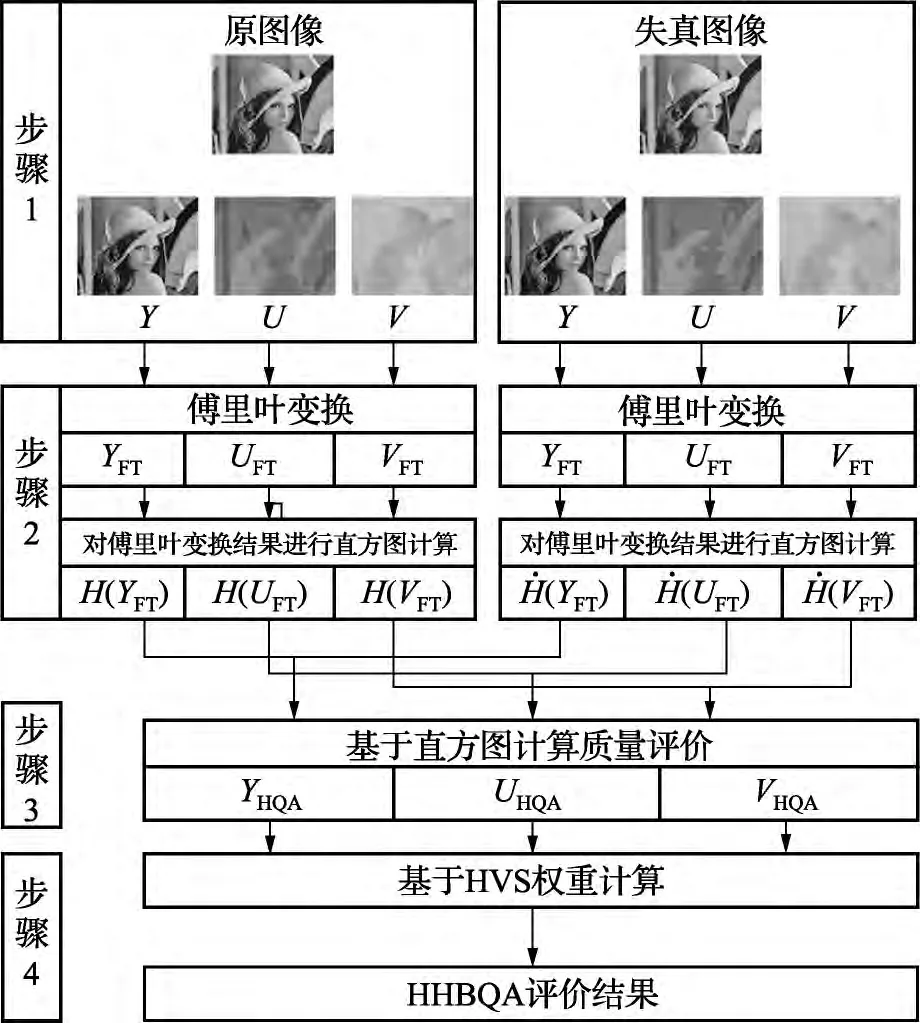
图3 HHBQA算法流程图

式中:CW表示视锥的感知权重;RW表示视杆的感知权重。

由上可得HPQA方程

以上权重算法从新的角度考虑了人眼视觉特性，不同于其他经典IQA算法，此为本算法一大创新。

3 实验结果与分析

图4所示为原Lena图像及一些Lena失真图像，利用一些失真方法(锐化、中值噪声、胡椒盐、JPEG压缩、高斯噪声和模糊化)对其进行失真处理，处理过程中保持失真图像与原图像PSNR值相同(均为27.67 dB)，尽管各图像PSNR值相同，但7幅图像仍有明显视觉感官差异，可见PSNR质量评价有时无效或者不精确。

图4 Lena原图像和几种失真处理后图像

第一组试验:各图像质量评价算法结果与真实人眼感知统计结果对比

1)为了对HHBQA进行性能衡量，利用 PSNR，PSNRHVS，MS-SSIM，SSIM和UQI进行图像质量评价的对比试验，利用MATLAB计算HHBQA质量评价结果，各质量评价方法结果如表1所示。

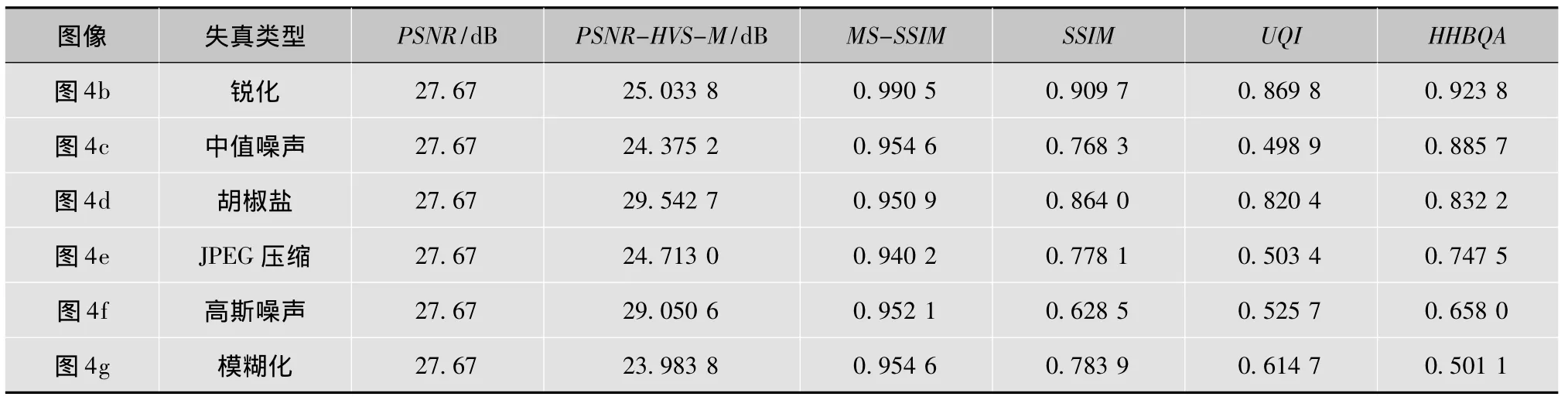
表1 不同失真类型的质量评价结果

2)为了对6幅失真图像的真实人眼感知效果做出检测，笔者请200位学生参与评价试验。学生根据自身真实感官评价6幅失真图像，并从作者设定的等级中(最好=6、很好=5、好=4、差=3、很差 =2、最差 =1)选择评价结果。人眼感知分数统计结果图如图5所示。

图5 失真图像的人眼真实感官统计结果

从对比试验可看出，PSNR-HVS-M结果显示图4d、4f质量优于其他图像，甚至优于原图像，明显与真实感官差异较大。MS-SSIM值显示图4e差于图4f、4g，与人眼真实感官统计结果不符;而且MS-SSIM各评价结果数值过于接近(算法敏感度不高)，而真实的人眼真实感官统计结果分布跨度较大，两者也不符。而SSIM和UQI的结果均显示图4g质量好于图4e和4f，显然与实际不符。而HHBQA结果与人眼真实统计结果具有高度一致性，同时评价结果跨度较大，与人眼感官统计结果一致(跨度也较大)。可见HHBQA的敏感度及准确度与真实感官接近，优于其他算法。本实验结合人眼感知系统证明HHBQA的性能。

第二组试验:HHBQA与其他质量评价算法在乘性斑点噪声失真下的质量评价结果对比

如图6所示为1幅Peppers原图和5幅经过乘性斑点噪声(均值=0，方差=0.06～0.86)处理的失真图像。

图6 原Peppers图像和5种斑点噪声处理后的图像

对图6中全部5幅失真图像计算各自PSNR，PSNRHVS-M，SSIM，UQI，MS-SSIM和HHBQA质量评价结果，结果如图7所示，可看出其他5种IQA算法随着方差值(σ2)均成指数分布，而HHBQA算法接近线性分布。对于乘性斑点噪声失真处理，理论上失真图像的视觉质量应该是随着方差值(σ2)呈线性下降而非指数性下降，所以本算法与理论最为接近。而其他5种质量评价算法不准确，与理论有一定差异。该实验从理论角度证明本算法的性能。

图7 经斑点噪声处理的Peppers图像评价结果随方差值的变化

第三组试验:HHBQA与其他质量评价算法的处理时间对比(计算所需时间)

质量评价算法所需处理时间也是一个重要参数，直接影响算法的实时性。本实验环境为:PC:Intel®Core i7 Q720(CPU 1.60 GHz，6 Gbyte内存)。利用 MATLAB2007对各质量评价算法进行了仿真，并对各算法所需的处理时间进行了统计(每个算法运行50次，然后取平均值)，结果见表2。

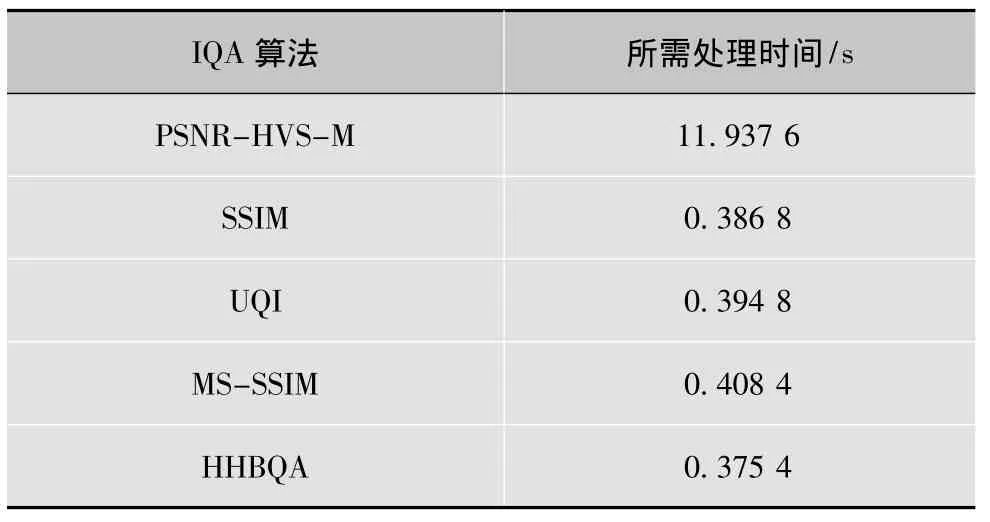
表2 不同质量评价所需处理时间

由表2可看出，本文算法计算所需时间最低，且大幅度低于PSNR-HVS-M。计算效率上，本算法有一定优势，具有较高的实时性，并有较高应用价值。

第四组试验:HHBQA与其他质量评价算法对失真的敏感度对比

从著名图像库(http://scien.stanford.edu/pages/labsite/scien_test_images_videos.php)选取12幅彩色图像如图8所示。(图8a～图8f size=341×512×3;图8g～图8 l size=512×341×3)，为了评价HHBQA在图像低失真下的敏感度性能，选择最低位比特替换数据隐藏的方式对图像进行失真处理(该方法造成的失真较小)。对所有12幅图像均进行最低位比特替换(LSB)数据隐藏处理(所有图像的隐藏数据相同(数据大小为1.5 bit/像素))。尽管对12幅彩色图像的数据隐藏失真处理参数一致，但理论上不同图像经数据隐藏后的视觉效果应该会有差异。处理后的失真图像评价结果如表3所示:可看出PSNR值均相同，无法判断出图像差异;PSNRHVS-M值非常接近(49.95～50.06);MS-SSIM除了图8a之外，其他11幅图像评价结果都一样;SSIM值更加接近(0.997～0.999);UQI值也非常接近(0.976～0.999);HHBQA值跨度较大(0.427～0.933)，敏感度较高。这是因为其他评价算法大多基于空间域计算，对于一些低失真，从空间域难以区分图像视觉效果差异。而本算法基于频率域计算，并结合HVS的权重分配，所以本算法对低失真的敏感度较高，可以明显区分失真图像的视觉效果差异。

图8 用作算法敏感度测试的图像原图

表3 经LSB处理过的图像(1.5 bit/pixel)质量评价结果

4 小结

针对已有的基于空间域图像质量评价算法准确度和敏感度不高的问题，本文设计了一种新的彩色图像质量评价算法，创新地利用频率域直方图和HVS计算图像质量。与已有同类算法相比，本文算法与真实视觉感官高度一致，对于低失真具有较好敏感性，本算法的计算过程也快于其他算法，在保持质量评价准确性的同时，具有实时性和高效性。

［1］高攀.一种基于颜色特征的图像质量评价算法［J］.电视技术，2012，36(16):98-100.

［2］ PONOMARENKO N，SILVESTRI F，EGIAZARIAN K，et al.On between-coefficient contrast masking of dct basis functions［C］//Proc.Workshop on Video Processing and Quality Metrics.［S.l.］:IEEE Press，2007.

［3］ WANG Z，BOVIK A C，SHEIKH H R，et al.Image quality assessment:from error visibility to structural similarity［J］.IEEE Trans.Image Processing，2004，13(4):600-612.

［4］ WANG Z，SIMONCELLI E P，BOVIK A C.Multiscale structural similarity for image quality assessment［C］//Proc.Thirty-Seventh Asilomar Conference on Signals，Systems and Computers.［S.l.］:IEEE Press，2003:1398-1402.

［5］谢斌，任克强，肖玲玲.一种基于HVS的DCT域稳健视频水印算法［J］.电视技术，2011，35(9):30-32.

［6］ FRIDRICH J.Digital image forensics［J］.IEEE Signal Processing Magazine，2009，26(2):26-37.

［7］ PEI SC，YEH M H，LUO T L.Fractional fourier series expansion for finite signals and dual extension to discrete-time fractional Fourier transform［J］.IEEE Trans.Signal Processing，1999，47(10):2883-2888.

［8］ CHEN SK，CHEW K S，MCNEILL D S，et al.Apoptosis regulates ipRGC spacing necessary for rods and cones to drive circadian photoentrainment［J］.Neuron，2013，77(3):503-515.