一种基于模糊逻辑的单交叉口信号控制方法

邓琼华,孙 琦

(无锡市政设计研究院有限公司,江苏无锡 214072)

一种基于模糊逻辑的单交叉口信号控制方法

邓琼华,孙 琦

(无锡市政设计研究院有限公司,江苏无锡 214072)

提出了一种单交叉口模糊信号控制方法,选取排队长度作为模糊控制器输入量,建立模糊控制规则库,并建立了车辆的延误模型。最后进行了计算机仿真,在多种车辆到达率的情况下,比较了模糊控制与传统的感应控制及定时控制的车辆平均延误,仿真结果表明,提出的控制方法能有效减少车辆在交叉口的延误,控制效果优于传统的控制方法。

交通信号控制；模糊控制；交叉口

0 引言

交叉口的信号控制是城市交通控制的关键。传统信号控制的缺陷是对不可预测的交通需求波动不能做出快速反应［1-2］；感应控制克服了定时控制的不足,在一定程度上能够适应交通需求的随机变化［3］。但传统感应控制所采用的延时算法依然是建立在精确数学模型基础上的,当交通状况复杂时表现为在绿灯时间的利用率偏低。

模糊控制不需要建立精确数学模型,而是以接近人的思维方式进行推理,因此具有更好的适应性。1977年希腊学者Pappis CP和英国模糊控制专家Mamdani E H. A［4］首次提出单路口交通信号灯模糊控制方法,此后国内外学者相继做了大量的研究。文献［5］提出了基于多相位的控制方案,但实际中交叉路口的各个方向的车流分布的不均匀性，会在一定程度上造成空间和时间上的浪费；基于这种情况，文献［6-7］又提出了变相位、变周期的控制方案,但这与驾驶员的心理及驾驶习惯有冲突,存在安全隐患。为解决以上不足,本文设计了一种模糊控制方法,通过计算机仿真,与定时控制、感应控制等方案进行了比较。仿真结果表明,本文提出的方法能够有效减少车辆在交叉口的延误。

1 模糊控制器的设计

以图1所示的交叉口为研究对象,实行的是两相位的信号控制。

模糊控制器的设计过程如下：

(1)确定输入及输出变量

有经验的交警往往根据排队长度来决定如何

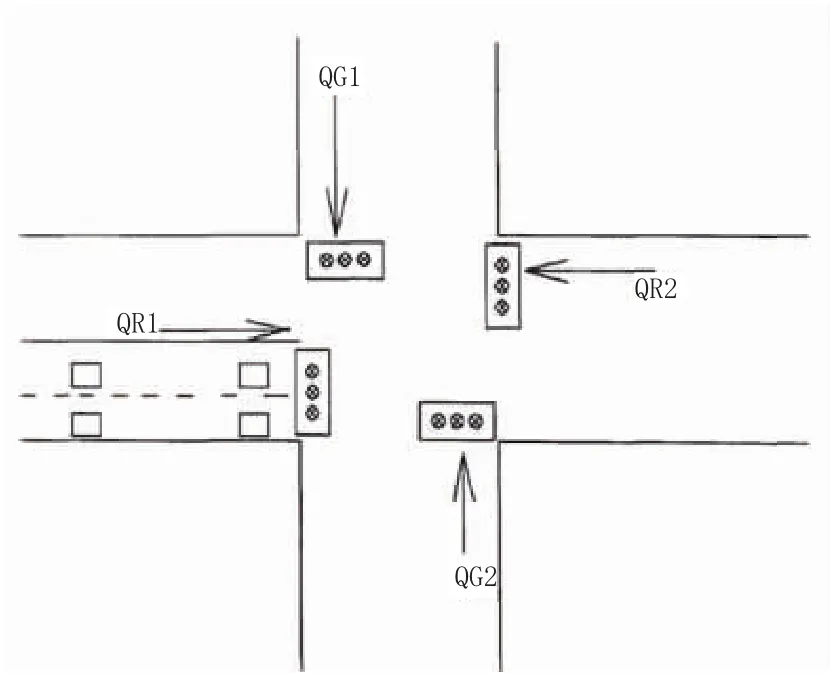
图1 交叉口示意图

(2)确定基本论域、论域及转换关系

本文选取当前相位排队车辆数基本论域确定为(0,36)；对应的论域确定为｛-6,-5,-4,-3,-2, -1,0,1,2,3,4,5,6｝。选定绿灯时间的基本论域：(16,56)。对应的论域为｛0,1,2,3,4,5,6,7,8｝。

根据线形插值可以确定模糊论域中的排队值w与真实值m之间的对应关系为：w=k×(m-b)；经插值运算得k=0.33,b=18。

绿灯时间真实值m与模糊论域中的值w之间的关系：m= w/R；经运算可得R=0.2。

(3)选取语言变量值

从交警指挥交通的思维出发,本文选择了“很长(VL)”,“长(L)”,“较长(RL)”,“中等(M)”,“较短(RS)”,“短(S)”,和“很短(VS)”等七个语言值来描述语言变量。

(4)定义语言变量的隶属函数

本文采用三角形隶属函数,输入变量QR的隶属函数见图2。

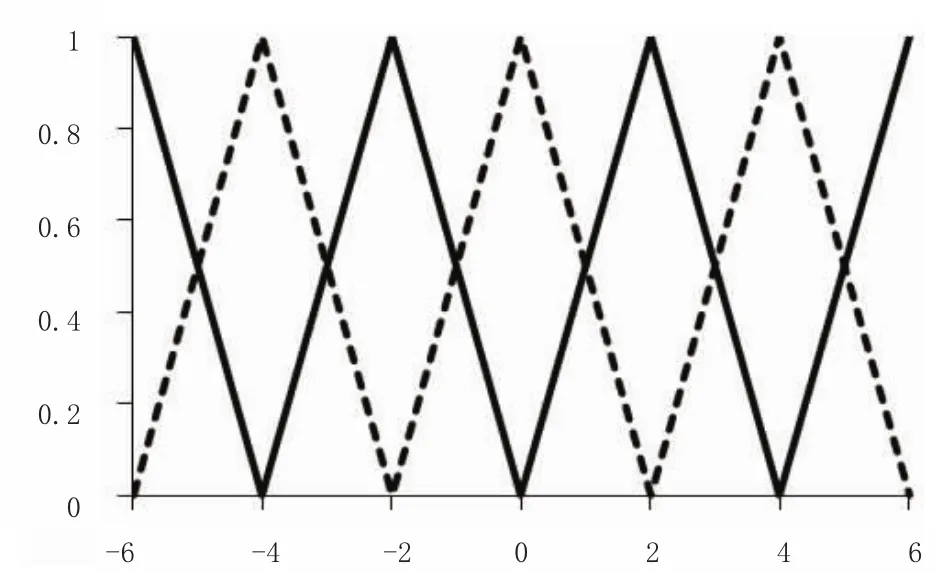
图2 隶属函数图

输入变量QG及输出变量GG的隶属函数与QR类似,不再重复给出。

(5)模糊规则的建立

充分借鉴交警经验及前人研究成果的基础上,本文所建立的模糊控制规则库见表1,规则曲面见图3。

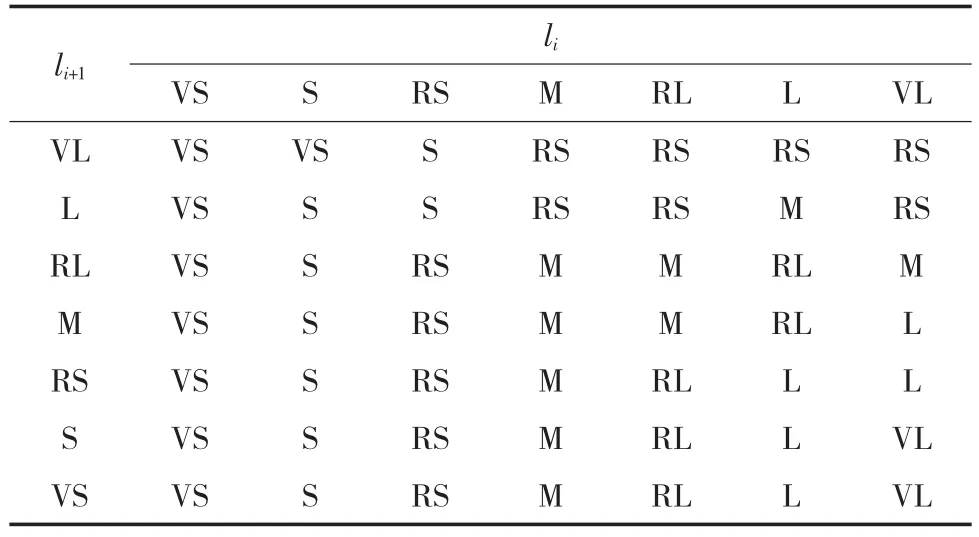
表1 模糊规则库

图3 模糊规则曲面图

2 仿真实验及结果分析

本文通过计算机仿真,对比分析定时控制、感应控制及本文提出的模糊控制三种控制算法下,车辆通过交叉口的平均延误。

使用MATLAB的模糊工具箱设计本文所提出的模糊控制算法,编程建立交叉口的延误模型,在运行过程中每个相位的结束时刻计算该相位的延误,同时调用模糊控制算法,实时输出下一相位的绿灯时间。

2.1 试验假设

综合考虑实际交通特性及编程的需要,本试验基于以下假设条件：

(1)以每5个周期(大约5 min)为一个仿真时间段,在该时间段内车辆按照固定的到达率均匀到达；

(2)取每仿真时间段中各个周期的车辆延误的平均值作为该到达率下的延误；

(3)平行对比试验分别选择基于F. Webster算法的定时控制及文献［3］提出的优化感应控制。

2.2 延误模型的建立

假定初始排队为零,先放行2相位G(0单位：s),则1相位红灯时间G0结束时的排队为L1=K1G0；对应2相位的排队L1=0。由L1、L2可以得出1相位的绿灯输出时间G1。第一个周期结束时, 1相位的排队长度X1=K1T-KLG1(若X1＜0,则令X1=0),延误为周期T内到达的车辆减去离去的车辆：对2相位做类似分析：当其红灯时间G(1也即1相位的绿灯时间)结束时,红灯方向的排队长度L1=K2G2,对应1相位的排队L2=X1；由L1、L2可以得出1相位的绿灯输出时间G2,同理X2=K2T-KLG(2若X2＜0,则令X2=0)；延误

不妨设第N(N=2,3,4…)个周期开始时1相位(红灯相位)的初始排队为X1,红灯时间Gn-1结束时相位1方向的排队L1=X1+Gn-1此时2相位(绿灯相位)的排队长度为L2=X2,由L1、L2能得出Gn,见图4。

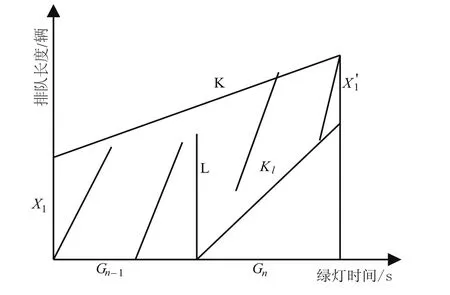
图4 第N个周期1相位的延误

由图4可知,当第N个周期结束时,1相位的排队X1=X1+K1T-KLGn；此时的延误D1=(2X1+K1T) T/2-KLG2n/2；［周期T=Gn-1+Gn］。

类似地,可以建立第N个周期2相位的延误模型。

2.3 实验结果分析

本实验共仿真了从0.01(辆/s)到0.25(辆/s)各种到达率下不同算法的控制效果。

针对不同的到达率,分别进行了5个周期的仿真,然后取其平均值作为图5中纵轴的数据。从图5可以看出,在各种到达率情况下模糊控制的车辆平均延误均小于定时控制及感应控制,随着车辆到达率的增加,这种优势越来越明显。

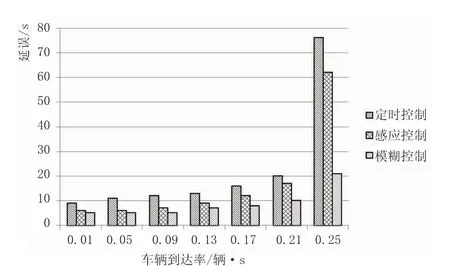
图5 延误比较柱状图

全部仿真结果数据见图6。从图6可以进一步看出：当车辆到达率较低时,模糊控制与感应控制下的车辆延误相差不大,都明显小于定时控制；当到达率大于0.22(辆/s)时感应控制及定时控制的延误都迅速增大,而模糊控制增幅相对较小。这是因为本文提出的模糊控制算法是在每个相位结束时根据检测到的排队长度实时输出下一相位的最佳绿灯时间,具有很强的适应性。而定时控制算法是一种基于历史数据的算法,对交通量波动较大的情况难以适应。感应控制的原理是在每相位末,如果检测到有车辆,则给予一定的绿灯延时,当交通车辆趋于饱和时,延时策略的效果会变差。

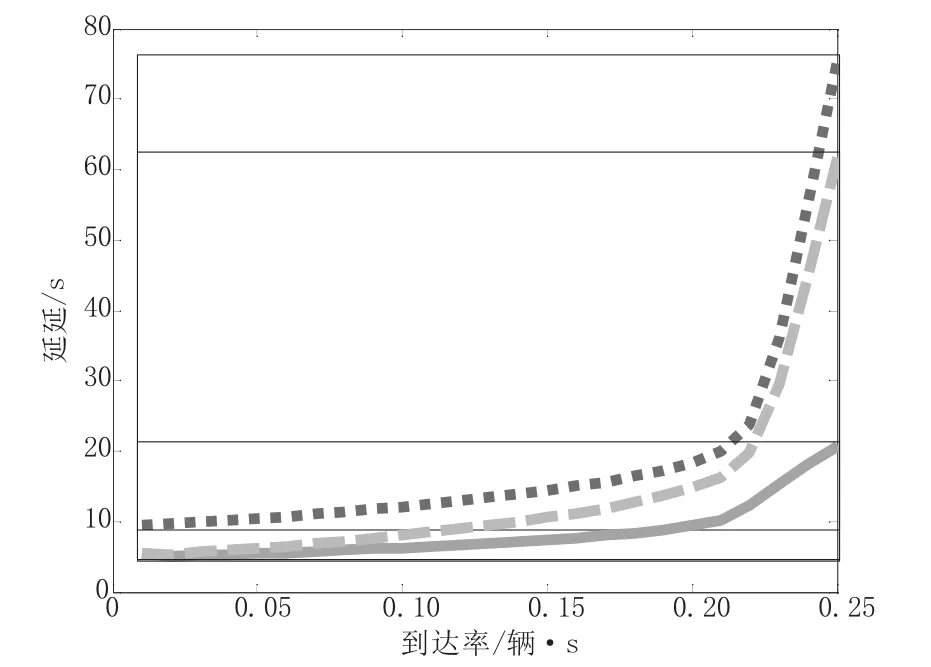
图6 延误比较曲线图

3 结论

本文提出了一种基于模糊逻辑的单交叉口信号控制方法,仿真结果表明,与定时控制及感应控制相比,该方法能有效减少车辆在交叉口的延误,适用于交通量变化大、饱和度较高的交叉口。

［1］ F.Webster and B.Cobbe.Traffic Signals［R］.HMSO，London，U.K.: Road Research Tech- nical Paper，1966.

［2］ 陈群，晏克非.基于遗传算法的城市交叉口实时信号控制研究［J］.交通与计算机，2005，23(1):15-18.

［3］ 李水友，刘智勇.城市交通感应控制综述［J］.城市交通，2006(6): 64-69.

［4］ Pappis C P，Mamdani E H.A fuzzy Controller for a traffic junction［J］.IEEE Transactions on System，Man and Cybernetics，1997(7): 707-717.

［5］ Junxia Gao，Jiangeng Li.Multi-phase Fuzzy Control Under Hybrid Traffic Flow of Single Intersection［J］.Intelligent Transportation Systems Proceedings，IEEE，2003(2):1329-1333.

［6］ 赵忠杰，刘小强.单交通路口变相位变周期信号控制［J］.长安大学学报，2005，25(6):70-72.

［7］ 臧利林，贾磊，林忠琴.基于模糊逻辑的交通信号控制与仿真研究［J］.公路交通科技，2006，23(4):124-127.

U491.5+1

A

1009-7716(2015)09-0009-003

2015-04-23

邓琼华(1988-),女,湖南武冈人,工程师,从事交通规划与管理研究工作。分配通行权,因此本文选取当前红灯相位及其冲突相位的排队长度作为输入变量,当前红灯相位的下一绿灯时间为输出变量。