信道中QPSK信号传输性能的仿真分析

王敬　王媛

摘 要：该文阐述了正交相移键控（QPSK）的基本原理， 以Matlab/Simulink 仿真软件为平台， 建立了加性高斯信道和多径衰落信道下的QPSK通信系统模型。对该信号在上述两种信道中的传输性能进行了仿真分析。结果表明信噪比相同时，信号在高斯白噪声信道中的可靠性优于多径衰落信道。如果不对多径衰落信道中的衰落进行补偿，则无法进行可靠传输。因此文中所做研究为QPSK调制技术在移动通信中应用打下基础。

关键词：正交相移键控；加性高斯信道；多径衰落信道

中图分类号：TN914.2 文献标识码：A 文章编号：1009-3044（2015）20-0045-03

Simulation Analysis of Transmission Performance for QPSK Signal in Channels

WANG Jing，WANG Yuan

（Fujian Nomal University MinNan Science and Technology Institute， Quanzhou 362332，China）

Abstract：This paper describes the basic principle of the quadrature phase shift keying （QPSK）， and builts the QPSK communication system model of Gauss channel and multipath fading channel based on Matlab/Simulink simulation software. The signal performance in the two channel are simulated and analyzed. The results show that the reliability of the signal in the Gauss channel is better than that of the multipath fading channel as the same SNR. If Without compensation， the reliable transmission can not be transmitted in the multipath fading channel. So the research is the foundation of the application of QPSK modulation technology in mobile communication.

Key words： QPSK；Gauss channel；multipath fading channel

1引言

QPSK（Quadrature Phase Shift Keying）是四相相移键控的简称，也叫正交相移键控，是现代通信中一种十分重要的数字调制方式。它具有较高的频带利用率和良好的抗噪声性能，在电路上实现也较为简单等一系列独特的优点，已经广泛应用于移动通信中。调制信号在各种干扰信道中的传输性能决定了调制技术的优劣，因此文中研究具有一定的必要性。

文中先概要介绍了QPSK调制技术的基本原理，然后以Matlab/Simulink 仿真软件为平台，建立高斯白噪声信道和多径衰落信道下QPSK通信系统模型，并对两种信道下传输性能进行了仿真分析。

2 QPSK基本原理

QPSK信号可以表示为：

[SQPSK（t）=2EsTscosωct+（i-1）π2] [0≤t≤TS]，i=1，2，3，4

式中[Es]为单位符号的信号能量，即[0≤t≤Ts]时间内的信号能量；[wc]为载波角频率，[Ts]为符号持续时间。

由上式知，QPSK利用载波的4种不同相位来表征数字信息，是一种四进制相移键控。为了能和四进制的载波相位配合起来， 需要把输入调制器的二进制数字序列转换为四进制。两个二进制码元中的前一比特用a来表示，后一比特用b表示，称为双比特码元ab，然后用4种不同的载波相位分别表征这4种数字码元。按ab分组与载波相位的对应关系有π/2体系（也称A方式）与π/4体系（也称B方式），具体定义如表1所示：

表1 双比特ab与载波相位的关系

[双比特码元ab＼&载波相位[?n]＼&a＼&b＼&π/2体系（A方式）＼&π/4体系（B方式）＼&0＼&0＼&0（0°）＼&5π/4（225°）＼&1＼&0＼&π/2（90°）＼&7π/4（315°）＼&1＼&1＼&π（180°）＼&π/4（45°）＼&0＼&1＼&3π/2（270°）＼&3π/4（135°）＼&]

QPSK信号可以看成两个正交载波进行双边带调制所得信号之和，即它可以等效为是对两个载波正交的2PSK调制信号的叠加。由QPSK信号的解调原理可知，它也可以采用与2PSK信号类似的相干解调方法来进行解调[1]。

3信道

在通信系统中，信道是不可或缺的一部分。信道是发送端和接收端的媒介，即可以传输信号，又不可避免的对信号产生各种干扰和噪声。按照干扰和噪声的种类，信道通常可以分为：加性高斯白噪声信道、多径衰落信道和Rician衰落信道等[1]。由于信道的固有特性及引入的干扰与噪声对无线信号的传输质量起着决定性的作用，因此研究信号在各种干扰信道的性能有一定的必要性。在此，选择在通信仿真中应用比较多的加性高斯白噪声信道、多径衰落信道进行研究，其他信道性能不在此赘述。

3.1高斯白噪声信道

加性高斯白噪声是最常见的一种噪声，无论信号是否存在，噪声均存在于各传输媒质中，包括有线信道和无线信道。从概率论角度去分析加性高斯白噪声，它表现为信号围绕平均值的一种整体取值服从高斯分布的随机波动过程。对于一维的高斯随机变量[x]，它的概率[p（x）]， 一般由下式确定[1]。

[p（x）=e-（x-μ）22σ22πσ] （1）

其中， [μ]为均值，在高斯白噪声中取0；[σ2]为方差，表现为信号噪声功率的大小。

由于AWGN信号易于分析、近似，因此在信号处理领域，一般先研究信号在加性高斯白噪声信道下的性能，然后再把它推广到更复杂的多径衰落信道。

3.2 多径衰落信道

移动无线信道的典型特点是：时变和多径。“时变”是指对信号的衰减和传输时延随时间变化；“多径”是指由于发送端和接收端之间建筑物或其他物体的反射、绕射、散射等引起的传输路径不止一条。由于多径反射和衰减的时变性会使各路信号经历不确定的随机波动，导致各路反射波的到达时间、相位也各不相同。而接收端接收到的信号是对多条路径信号进行同相加强，反相减弱的叠加，使得接收信号幅度急剧变化而产生衰落。这种衰落是由于多径现象引起的，所以称为多径衰落。多径衰落使接收信号的质量变差， 严重影响通信质量的可靠性 [2].

由于无线信道的复杂性，为了方便分析，接下来建立数学模型来分析。

假设信道的输入是一个经过调制的信号，其形式为：

[s（t）=Acos（2πfc（t）+φ（t））] （2）

在N条路径的条件下，由于每条路径衰减和时延都是时变的，所以到达接收端信号是各路径信号的合成可表示为：

[y（t）=Ai=1N[ai（t）cos（2πfc（t）+φi（t））]=A（x1（t）cos2πfc（t）-x2（t）sin2πfc（t））] （3）

在（3）式中，[x1（t）=i=1Nai（t）cosφi（t）]，[x2（t）=i=1Nai（t）sinφi（t）]，[ai（t）=x21（t）+x22（t）]。其中[ai（t）]为第[i]条路径到达接收端时的信号幅度；[φi（t）]为第[i]条路径的传输时延。

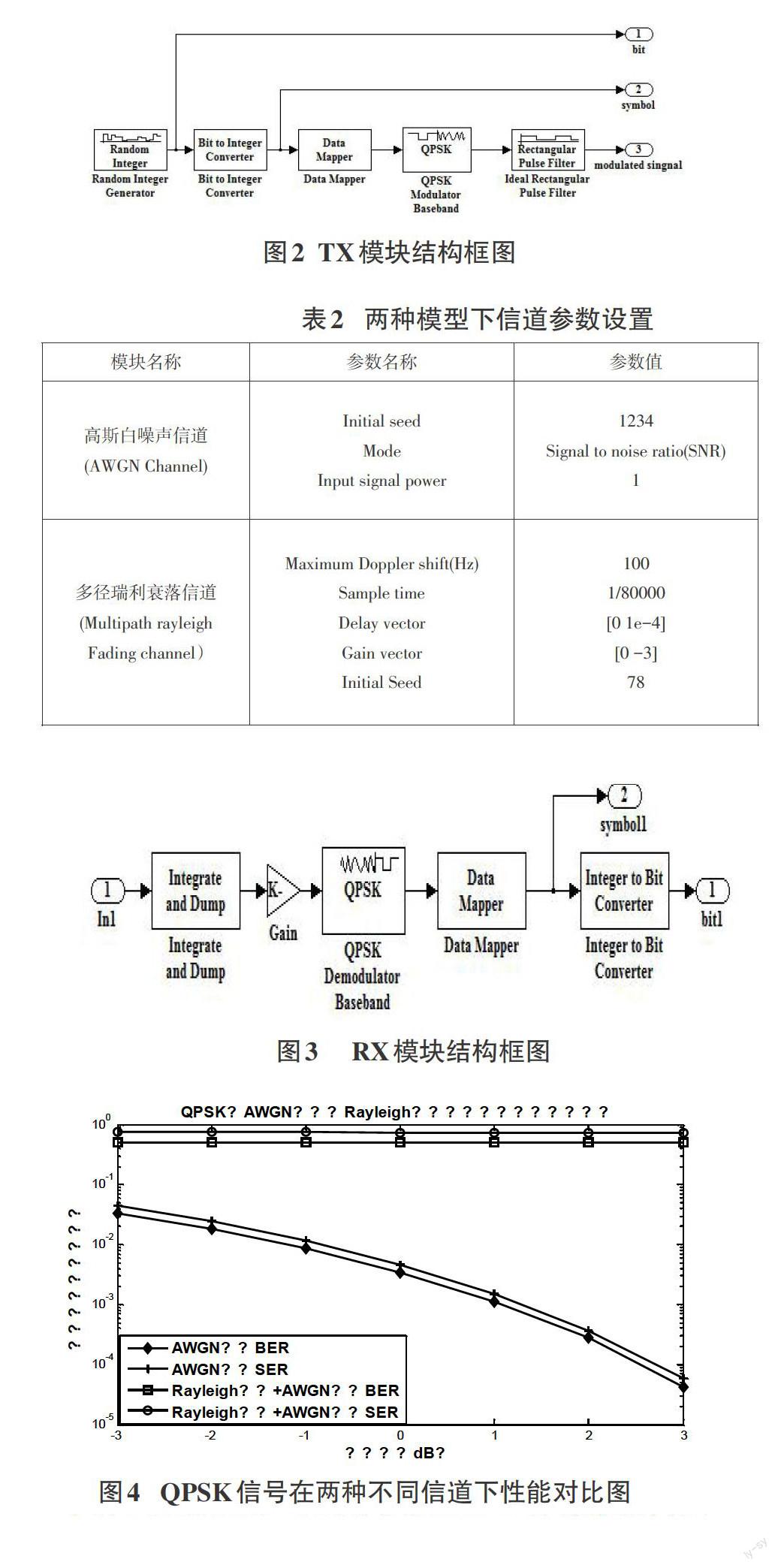
当路径条数N足够大时，[x1（t）]和[x2（t）]是服从均值为0，方差为[σ2]的高斯随机过程，接收信号的包络[ai（t）]服从瑞利分布。由瑞利分布定义，一个服从瑞利分布的变量Z的概率密度可表示为[3]：[p（z）=zσ2exp（-z22σ2），（0

在式（4）中，[σ2]是决定瑞利分布的参数。可以以得出，瑞利随机变量Z的均值为[（π/2σ）]，方差为[（4-π）σ2/2]，所以常用瑞利信道作为多径衰落的代表来研究。在仿真衰落信道时，两个重要的参数是多径扩展和多普勒带宽。

3.3 QPSK信号在信道中的性能指标

QPSK信号在信道中传输，会受到信道中噪声干扰导致接收端出现错误。传输性能的优劣主要由差错率来衡量，差错率越小，可靠性越高，抗干扰能力越强。差错率也有两种表达方式：误符号率与误比特率。

1）误符号率：又叫误码率（SER），指接收到的错误码元数和总的传输码元个数之比。

2）误比特率（BER）：是指接收到的错误比特数和总的传输比特数之比。

4 QPSK信号在不同信道下的性能仿真

在了解常用信道特点后，根据通信系统的一般模型，借助Matlab软件自带Simulink模块搭建不同信道下QPSK通信系统模型，进行仿真，并对QPSK信号通过信道后的差错率进行结果分析[4]。

4.1 系统顶层模型

以高斯信道为例，借助Simulink模块搭建高斯信道下QPSK通信系统模型[5～7]。顶层模型如下图1所示。其中TX模块为发送端，是一个子系统。它用来把信源产生的比特信息转换成相应的符号并送到QPSK调制模块进行调制，然后调制信号通过高斯白噪声信道（AWGN Channel）模块进行传输最后到达接收端RX。RX模块也是一个子系统，它负责完成QPSK信号的相干解调，恢复出初始数据比特和符号。

图1 系统顶层模型图

4.2 主要模块介绍

1）TX模块

TX模块的结构框图如图2所示。整个过程是：由随机数产生（Random Integer Generator）模块产生原始数据比特一方面作为信源模块的输出信号， 另一方面经过比特到整数转换（Bit to Integer Converter）模块将比特数据转换成对应的符号；再经过数据映射（Data Mapper）模块完成对符号的Gray编码；再送入基带调制器（ QPSK Modulator Baseband） 模块， 对数据进行QPSK调制；最后在经过理想矩形脉冲成形滤波器模块完成脉冲成形，得到调制后的QPSK信号。

图2 TX模块结构框图

2）信道

AWGN信道模块是为了将噪声叠加到TX模块产生的QPSK调制信号中。需要注意的是在进行多径衰落信道的仿真过程中，只需要在AWGN信道模块前添加多径衰落信道（Multipath Rayleigh Fading Channel）模块。这样可以满足信号不仅受到信道衰落的乘性干扰，同时还需要受到信道中高斯白噪声的加性干扰，使仿真过程更接近实际传输。两种模型下信道参数设置如表2所示：

表2 两种模型下信道参数设置

[模块名称＼&参数名称＼&参数值＼&高斯白噪声信道

（AWGN Channel）＼&Initial seed

Mode

Input signal power＼&1234

Signal to noise ratio（SNR）

1＼&多径瑞利衰落信道

（Multipath rayleigh

Fading channel）＼&Maximum Doppler shift（Hz）

Sample time

Delay vector

Gain vector

Initial Seed＼&100

1/80000

[0 1e-4]

[0 -3]

78＼&]

3）RX模块

RX模块的结构图如图3所示，它的输入端口模块In1连接TX模块的输出端口3代表已调制QPSK信号先经过积分清除（Integrate and Dump）模块完成对抽样数据的累加，再经过增益（Gain）模块完成对累加数据的归一化；再送入基带解调器（ QPSK Demodulator Baseband） 模块， 对数据进行QPSK信号进行解调，得到Gray编码；然后再经过数据逆映射模块将Gray编码转换成原始四进制符号；最后再将四进制符号转换成原始二进制比特信息。

图3 RX模块结构框图

4）误比特率与误符号率计算模块

误比特率和误符号率计算（Error Rate Calculation）模块是将原始输入比特、符号与解调后的比特、符号进行比较，并计算比较结果。

5系统仿真与结果分析

信号经过调制、信道、解调过程。在接收端，将得到的数据与原始信号源数据比较，得到在特定信噪比下的误码率。改变系统信噪比，从而得到系统的误码率曲线图。为了得到不同信噪比下的误码率和误比特率需要编写脚本文件，并与模型放于同一目录。将仿真时间和信噪比设置为与脚本文件一致，对所有模块参数设置，然后开始进行仿真，仿真结果如下图4所示：

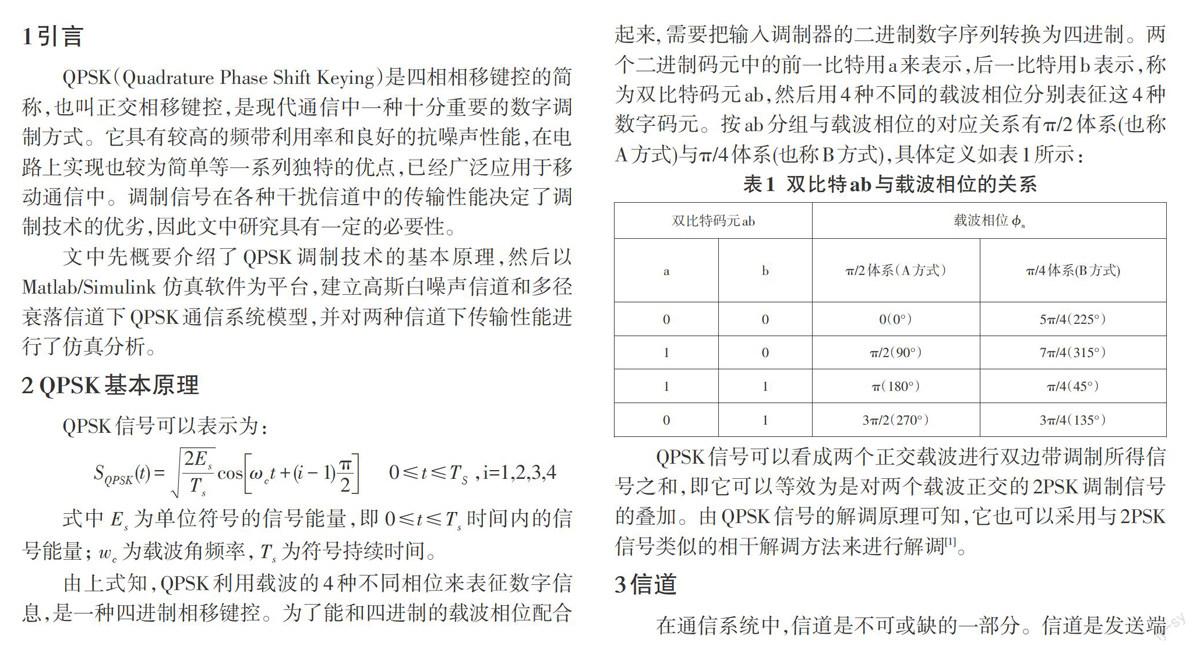
图4 QPSK信号在两种不同信道下性能对比图

由图4中可以看出：在两种信道下QPSK信号的误比特率均小于相应的误符号率；随着信噪比的增加，QPSK信号在高斯白噪声信道下的误比特率和误符号率均会降低，而在多径衰落信道中二者变化不明显；对于相同的信噪比， QPSK信号经过多径衰落信道后，误符号率和误比特率大大高于高斯白噪声信道下的误符号率和误比特率。例如当信噪比=1dB时，多径衰落信道误比特率SER接近100，而高斯白噪声信道的误比特率接近10-3，因此如果不对衰落进行补偿，则无法得到与高斯白噪声信道相同的传输效果，导致可靠性更差。由于在移动通信中信道衰落是不可避免的，因此，经常采用信道估计校正接收信号或者采用其他对信道相位变化不敏感的调制技术的方法来提高通信系统的性能。

6 结语

本文在研究QPSK调制原理和信道相关知识的前提下，以Matlab/Simulink为平台建立QPSK通信系统模型，并对两种典型信道下模型进行仿真分析。仿真结果表明QPSK信号经过多径衰落信道比高斯白噪声信道后的可靠性更差。因此，在多径衰落信道中传输时，如果不采用相关措施来补偿衰落，是无法进行可靠通信的。

参考文献：

[1] 樊昌信. 通信原理（第六版）[M].北京：国防工业出版社，2006： 196-213.

[2] 张志涌.精通MATLAB6.5版[M].北京：北京航空航天出版社， 2003.

[3] 张清泉， 行小帅.BFSK信号在高斯和瑞利信道中传输性能仿真分析[J].山西师范大学学报（自然科学版）.2010，3（24）：64～66.

[4] 邓华.MATLAB通信仿真及应用实例详解[M] .北京：人民邮电出版社， 2003：1-20.

[5] 刘学勇.详解MATLAB/Simulink通信系统建模与仿真[M]. 北京：电子工业出版社，2015：96-123.

[6] 张丽丽，陈伟.多径衰落信道中QPSK信号传输特性的研究[J].武汉理工大学学报（信息与管理工程版），2007，29（12）：43-46.

[7] 张小红，易称福，陈宇环.基于Rayleigh 信道模型下的性能分析与仿真[J].江西理工大学学报.2006，27（1）： 23-26.