基于MATLAB程序对于偏置曲线的实现

白庆月 邱泽阳

（兰州交通大学 数理学院，甘肃 兰州 730070）

基于MATLAB程序对于偏置曲线的实现

白庆月 邱泽阳

（兰州交通大学 数理学院，甘肃 兰州 730070）

基于等距偏置曲线的研究与实现，变距偏置曲线的研究迫在眉睫。本文结合数学思想的理论依据，对非正则偏置曲线进行MATLAB仿真实现，以求为完善非正则偏置曲线的研究领域贡献一份力量。

偏置曲线； MATLAB仿真； 曲线拟合

本文在等距偏置曲线的已有研究成果的基础上，着力向变距偏置曲线的领域进行探索和研究［1］。然而，在偏置曲线的实现上，等距偏置和变距偏置之间既有区别又有联系，造成复杂性的原因是偏置距离从常数向函数的转化。

1 偏置曲线理论

等距曲线是几何造型操作中的基本功能之一，由于其具有丰富的几何结构，在CAD的实际应用中发挥重要作用［2］。偏置曲线与基曲线之间总存在着一定的偏差，一般会以大量的代数距离作为衡量标准［3］。然而，偏置的自由有理曲线在偏置的过程中时而会出现无理的情况，基于此，变距偏置曲线当前的关键任务是采取拟合方法去逼近一条有理曲线［4］。

1.1 等距偏置曲线

等距曲线、曲面，是由已知曲线或曲面上的点沿其法线方向移动固定距离后所形成的曲线或曲面。

1.2 变距偏置曲线

变距曲线是等距曲线的延伸，当法向偏置距离是一个实值函数时，偏置距离函数d（ t）决定了偏置距离的可变性，随之出现的问题就是将会使变距偏置曲线和曲面变得更加的更复杂的形式。

2 偏置曲线的模拟实现

从参数曲线的定义中可知，由（n+1）个控制点pi方便定义一条曲线，而定义的n次bezier曲线是由前后n个控制点定义的两条n次曲线的线性组合。如下图表1是一组任意给定的8组数据的原始坐标点：

从这组离散的数据中得到基曲线的多项式表达式是下：

如右图1：是通过原始数据用MATLAB软件对原始数据的模拟仿真.

2.1 等距偏置曲线数值模拟

2.1.1 当偏置距离d＞0时有如下表二、表三中的数据是对应点的斜率、对应斜率与x轴的夹角θ：

表1

表2

表3

表4

表5

表6

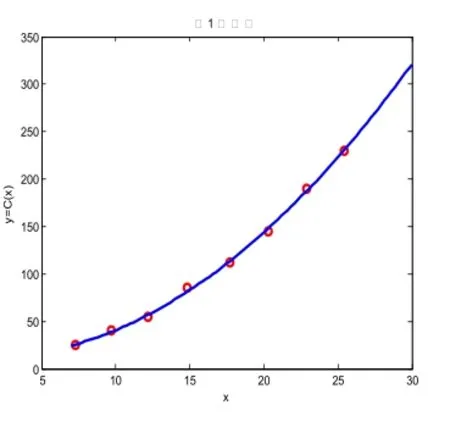
图1 原始曲线

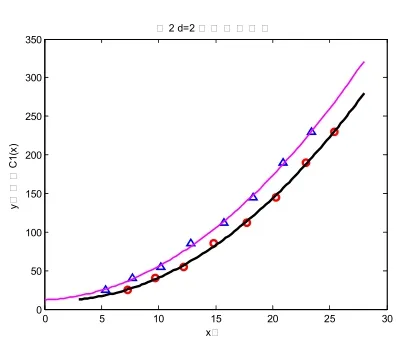
图2

图3

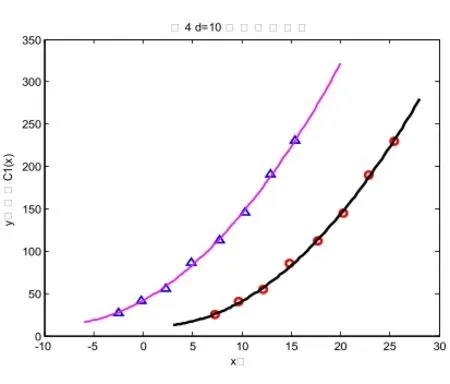
图4

图5

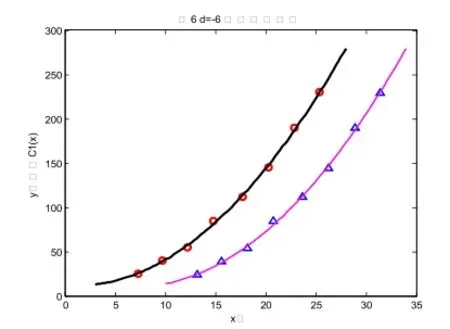
图6

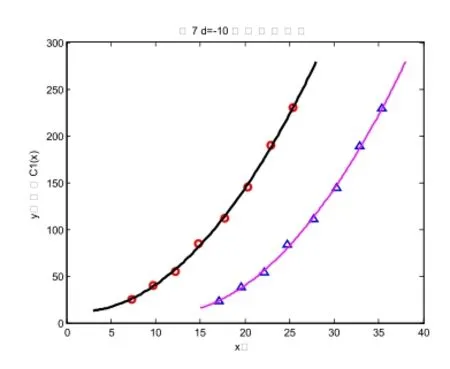
图7

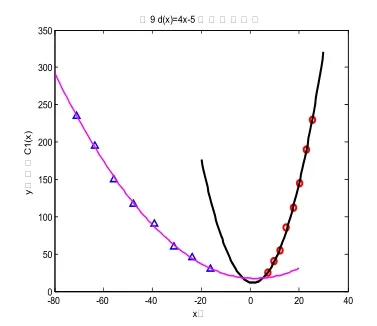
图8

图9

图10

以下表四是在选取d=2时得到的一些离散数据对应原始数据得到的离散点：

根据偏置的离散点得到新的拟合曲线多项式的方程系数。

如上图是用MATLAB软件模拟的等距偏置曲线，参数选取d=2、d=6、d=10时，对应图2、图3、图4.

2.1.2 当偏置距离d＜0时，有如下表五对应原始数据得到的内偏置的离散点：

如下图5、6、7依次是偏置距离参数选取d=-2、d=-6、d=-10的图像。

发现：偏置距离的正负决定了偏置曲线的方向。

2.2 变距偏置曲线数值模拟

如右图8是当偏置距离函数是d（ x）=4x-5时的偏置图像。

3 优化程序后的偏置实现

由于理论上的距离和实际在操作实现时总会有一些差别，所以对于坐标轴也需要一定的控制。改进后如下图9、图10：

4 总结

在国内对等距偏置曲线的研究基础上，对变距偏置曲线进行研究、并给与算法分析和实例验证。从偏置情况看到，当偏置距离变化时基曲线和偏置曲线就会出现相交的情况，这部分工作，我们将在后续的研究中进行去自交的算法探索和研究。

［1］ 施法中.计算机辅助几何设计与非均匀有理B样条.北京：高等教育出版社，2001.

［2］ 郭清伟.等距曲线有理逼近的一种方法.应用科学学报，2006，24（3）：278：281.

［3］ Maekawa T.An overview of offset curves and surfaces.Com puter-Aided Design，1999，31（3）： 165-173.

［4］ Elber G. Trimming local and global self-intersections in offset curves using distance maps. In：Proc. of the 10th IMA conference on the mathematics of surfaces. 2003. p. 213-22.

［5］ Elber G， Cohen E. Error bounded variable distance offset operator for freeform curves and surfaces. International Journal of Computational Geometry & Applications 1991；1（1）：67-78.

O187.1

A

1003-5168（2015）11-265-02

白庆月（1987-），女，山西朔州，硕士，主要研究方向：计算数学、 计算几何。

国家自然科学基金资助（61262044）非正则变距偏置曲线曲面的研究与应用