基于Mathcad的三维桁架有限元分析

李清富 任高杰

（郑州大学水利与环境学院，河南 郑州 450001）

基于Mathcad的三维桁架有限元分析

李清富 任高杰

（郑州大学水利与环境学院，河南 郑州 450001）

利用Mathcad的计算优势与编程特点，根据普通杆件的单元刚度矩阵和整体平衡方程，将Mathcad和有限元方法相结合，推导出任意形式的三维桁架结构的刚度矩阵在Mathcad中的表达形式；结合工程实例进行计算，求解出三维桁架的杆件内力与支座反力，并与Midas Civil建模结果对比验证，结果表明：将Mathcad与有限元相结合，能够在满足工程精度要求下高效率地进行三维桁架结构的力学分析。

Mathcad；有限元；三维桁架

Mathcad是一款工程计算软件，它具有线性及非线性方程求解与优化、常微分方程和偏微分方程求解、统计金融分析、信号和图像处理等许多方面的功能，并且提供丰富的接口可以调用第三方软件的功能，利于自行扩展和利用别的软件扩展功能。

1　三维桁架单元总体刚度矩阵推导

图1　局部坐标系与整体坐标系

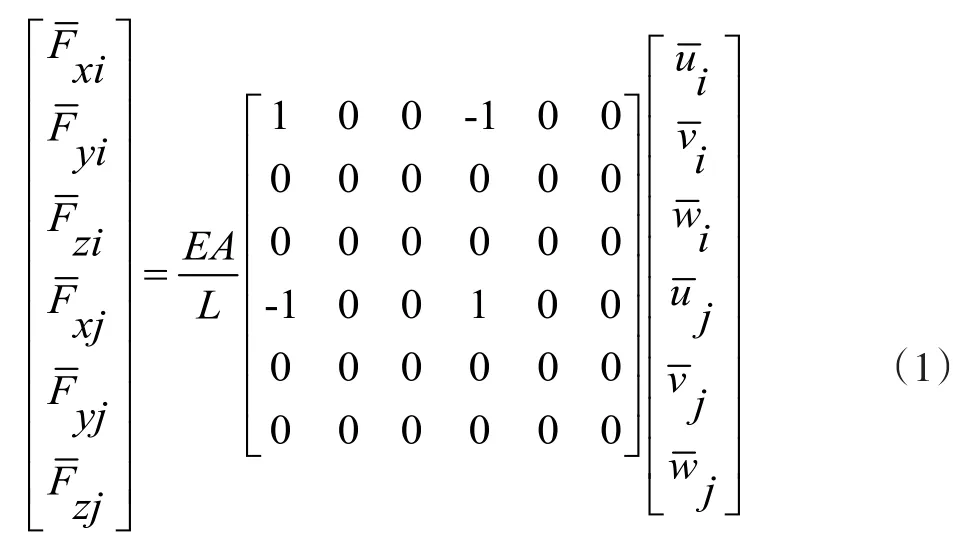
首先假设在三维直角坐标系中，杆件正好位于局部坐标系X¯轴，如图1所示。由于杆件两端点存在//三个方向的位移μ/ν/ω和三个方向的力Fx/Fy/Fz。因此杆件的平衡方程可以写成式（1）所示的矩阵形式。当X轴和杆的方向不一致时，如图，此时需要进行坐标转换。在空间整体坐标系中，任意向量（X，Y，Z）换算到局部坐标系（）中的换算关系可以用式（2）表示。

其中，cos（x， y）表示局部坐标系X2轴与整体坐标系X轴夹角的余弦，其余依次类推。为了书写方便，记

对于杆单元两端点所受的力和两端点位移可以通过相应的矩阵形式得到，因为C2是对称矩阵，CT=C-1，可得到三维桁架单元的整体平衡方程［2］，见式（3）：

2　实例分析

如图2所示，有一机架由空间桁架杆组成，其杆件单元的横截面积为15 cm2，由钢制成（E=200GPa），用Mathcad进行编程，求解各个杆件的内力。

图2　工程实例

具体求解过程如下：

2.1根据Top矩阵以及各节点坐标求出各杆件的单元刚度矩阵，如式（4）所示：

2.2单元刚度矩阵组装成总体刚度矩阵K，K的行列式为零，表明其不可逆，必须根据边界条件对其修正［4］，修正后的总体刚度矩阵为Kmod。

2.3可见修正后的Kmod行列式不为零，利用修正后的总体刚度矩阵求解各节点位移，然后根据节点位移求解支座反力和杆件内力，计算结果见表1、表2。

表1　支座反力结果对比（单位：KN）

表2　杆件内力结果对比（单位：KN）

2.4与Midas Civil建模结果进行对比

为了校验以上编程求解结果的精确性，利用Midas Civil对文中的工程实例进行了建模分析，Midas Civil计算结果与Mathcad编程结果如表1所示，结果表明：利用Mathcad的编程计算结果和Midas civil的建模计算结果一样，接近于理论解。

3　结语

本文的研究结果表明，基于Mathcad的三维桁架有限元分析结果满足工程精度要求，同时根据Mathcad的编程特点，对于其他的三维桁架结构，只需要改变编程过程中的Top矩阵和节点坐标就可以直接计算出任意三维桁架单元的内力和各约束节点的支座反力。

［1］张晓丹，李祥林，李晓红等.数学实验：Mathcad在数学实验中的应用［M］.北京：北京航空航天大学出版社，2012.

FiniteElement Analysisof 3-D Trussbased on Mathcad

Li Qingfu Ren Gaojie
（School of Water Conservancy&Environment，Zhengzhou University，Zhengzhou Henan 450001）

By the calculation advantages and programming characteristics of Mathcad，on the basis of element stiffness matrix and the general balance equation of ordinary bar，Mathcad and finite element method are combined to deduce stiffness matrix expressive of any 3-D truss structures in Mathcad；support reaction and internal force of the 3-D truss are calculated through an engineering example and compared with the Midas Civil modeling results，it turns out that combining Mathcad and finite element method could carry out a high-efficient mechanism analysis of 3-D truss meeting the precision requirement of engineering.

Mathcad；finite element method；3-D truss

TU323.4

A

1003-5168（2015）12-0095-2

2015-12-11

李清富（1966-），男，博士，教授，研究方向：结构工程领域的研究。