Lie-Poisson框架下一个新的有限维完全可积系统

薛珊 石磊

（河南交通职业技术学院基础部，河南 郑州 450000）

Lie-Poisson框架下一个新的有限维完全可积系统

薛珊 石磊

（河南交通职业技术学院基础部，河南 郑州 450000）

研究一个3×3特征值的非线性化，证明此3×3特征值问题的非线性化是Poisson流形上具有Lie-Poisson结构的广义Hamilton系统.并用母函数法证明了其可积性.

Lie-Poisson结构；Hamilton系统；非线性化特征值问题

有限维可积系统的构造重要途径之一是特征值问题的非线性化，以往特征值问题的非线性化研究是在辛流形框架下通过非退化的Poisson结构展开的［1-4］.本文首先用Lenard递推方程，得到与谱问题（2）相对应的1+1维孤子族.然后，在位势与特征函数约束关系下，（2）被非线性化为Poisson流形上具有Lie-Poisson结构的有限维Hamilton系统［5-7］.最后，证明了该Hamilton系统的可积性。

1 1+1维孤立子方程族

为了得到1+1维孤立子方程族，我们首先引入Lenard递推方程其中

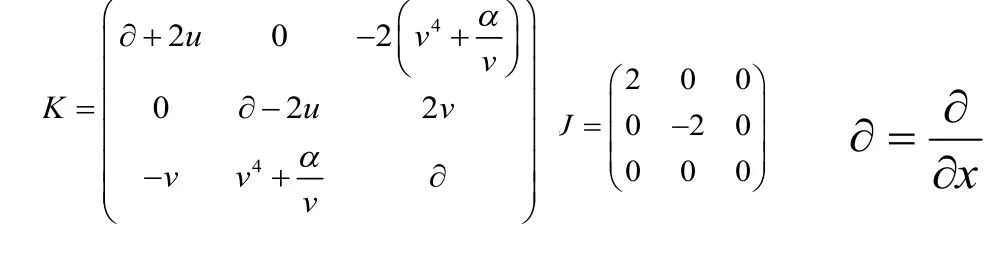
a∈R，u，v为位势.其前几个解为：

考虑Lenard谱问题

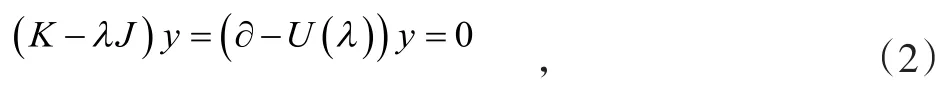
其中

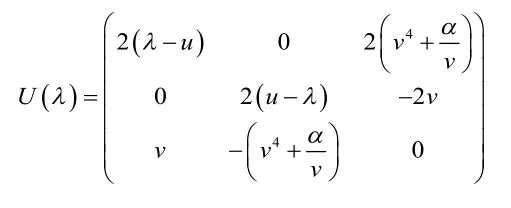
定义映射σ：R3➝sl（3，R）为

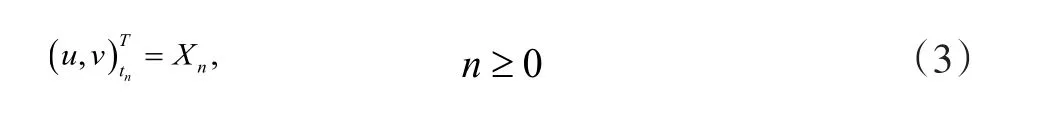
对比（1），我们有

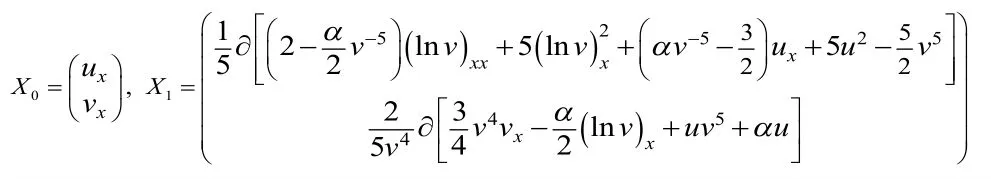
2 非线性化的特征值问题及其Lie-Poisson结构

取一组两两互异且不等于零的常数λ1，…，λN，考虑

经过简单计算，我们有：

由于算子J的核为一维的，其生成元为g-1，因此

若c=0，则特征函数与位势的约束关系为

把（6）代入（4），我们得到非线性化的特征值问题

其中

下面说明系统（7）的Hamilton结构.考虑Lie代数，

其中

选择LA的一组基ε1，ε2，ε3，分别为

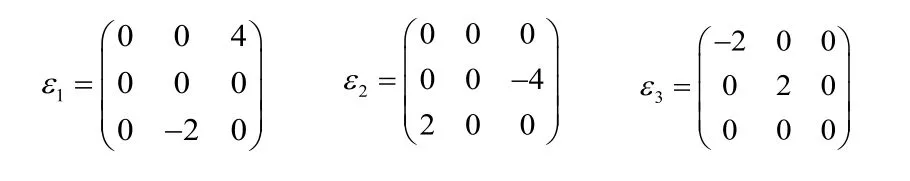
因此，Jj为LA的Lie-Poisson结构矩阵［8］，上的Lie-Poisson括号为

3 证明系统（7）的完全可积性

在（6）成立的条件下，根据方程（5）可知

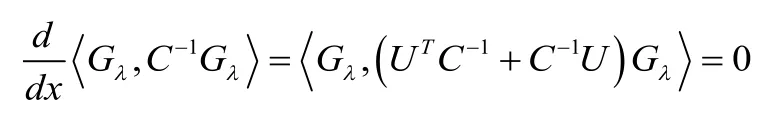
命题3 h1，…，hN是Poisson结构（8）的N个函数独立的Casimir函数。

记Fλ-流的变量为tλ，则

其中

推论6

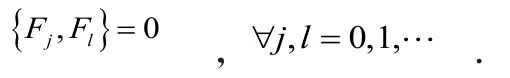
利用文献[5-7]的方法，可以证明下面结论：

由命题3，推论6和命题7，得Hamilton系统（7）具有N1个函数独立的Casimir函数个函数独立且两两对合的守恒积分所以是完全可积的。

[1]CAO Cewen,GENG Xianguo.Classical integrable systems generated through nonlinearization of eigenvalue problems[M]. Proc.Conf.on Nonlinear Physics(Shanghai 1989),Research Re⁃ports in Physics.Berlin:Springer,1990.

[2]曹策问.AKNS族的Lax方程组的非线性化[J].中国科学,1989（7）:701-707.

[3]CAO Cewen.A Classical integrable system and the involu⁃tive representation of solutions of the KdV equation[J].Acta Math.Si⁃nica,New Series 1991(7):216-223.

[4]CAO Cewen,WU Yongtang,GENG Xianguo.Relation be⁃tween the Kadometsev-Petviashvili equation and the confocal invo⁃lutive system[J].J.Math.Phys,1998,40:3948-3970.

[5]DU Dianlou,CAO Cewen,WU Yongtang.The nonlinearized eigenvalue problem of the Toda hierarchy in the Lie-Poisson frame⁃work[J].Phys.A,2000,285:332-350.

[6]DU Dianlou,CAO Cewen.The Lie-Poisson representation of nonlinearized eigenvalue problem of the Kac-van Moerbeke hier⁃archy[J].Phys.Lett.A,2001,278:209-224.

[7]DU Dianlou.Complex form,reduction and Lie-Poisson structure for the nonlinearized spectral problem of the Heisenberg hierarchy[J].Phys.A,2002,303:439-456.

[8]Olver P J.Applications of Lie Groups to Differential Equa⁃tions[M].2nd ed.Berlin:Springer,1993.

A New Finite-dimensional Integrability Systemin theLie-Poisson Framework

Xue Shan Shi Lei
（Foundation Department of Henan College of Transportation，Zhengzhou Henan 450000）

The nonlinearization of a 3×3 eigenvalue is studied.It is proved that the nonlinearized of this 3×3 eigenvalue problem is a generalized Hamiltonian system with a Lie-Poisson structure on the Poisson manifold.Furthermore，the generating function method is used to prove its integrability.

Lie-Poisson structure；Hamiltonian system；nonlinearized eigenvalue problem

O175.9

A

1003-5168（2015）12-0082-3

2015-12-11

河南交通职业技术学院院级科研项目（2015-YJXM-024）。

薛珊（1982-），女，硕士，讲师，研究方向：孤立子与可积系统。