基于多卡GPU集群的多次波逆时偏移成像技术
朱 博,宋 鹏,2,李金山,2*,谭 军,2
(1.中国海洋大学海洋地球科学学院,山东青岛266100;2.中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛266100)
基于多卡GPU集群的多次波逆时偏移成像技术
朱博1,宋鹏1,2,李金山1,2*,谭军1,2
(1.中国海洋大学海洋地球科学学院,山东青岛266100;2.中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛266100)
相对于常规逆时偏移,多次波逆时偏移成像技术具有更高的成像精度。在分析多次波逆时偏移成像原理和条件的基础上,对多次波逆时偏移成像中的多次波预测、波场延拓等步骤的实现过程进行了研究。在此基础上,利用Sigsbee2B地质模型,应用基于反馈环理论的自由界面多次波衰减方法预测得到纯多次波炮集,实现了基于多卡GPU集群的多次波逆时偏移成像处理。处理结果显示,多次波逆时偏移的中浅层成像清晰,构造的成像精度明显高于常规逆时偏移。多卡GPU集群的应用可显著提高多次波逆时偏移的计算速度和效率,使得基于地震大数据体进行多次波逆时偏移成像处理成为可能。
多次波波场延拓逆时偏移成像多卡GPU成像精度
逆时偏移方法于20世纪80年代由Whitmore等[1-3]首先提出。其核心为基于双程波动方程,应用有限差分等数值模拟手段来实现波场的正时与逆时延拓,并通过正时波场与逆时波场的互相关来实现成像。经过几十年的发展,逆时偏移技术无论是在理论上还是在实用性方面都取得了长足的进步。但是,由于常规逆时偏移多是基于一次反射波来实现成像处理的,其间会将多次波视为干扰进行剔除。而常规逆时偏移在一次波无法到达的阴影区或一次波照明度较低的区域会遇到成像困难的问题。事实上多次波也是地震波在地下介质中传播形成的反射波。与一次反射波相比,多次波在地下传播的射线路径更长,覆盖的区域更广,地下照明度更加均衡,甚至其能够照射到一次反射波无法到达的阴影区,从而克服成像困难的难题。近年来研究人员已经对多次波逆时偏移成像技术开展了诸多卓有成效的研究工作。当前应用多次波进行逆时偏移成像的方法主要有2类:第1类方法需先将多次波转化为准一次波,然后应用常规逆时偏移算法对准一次波进行成像[4-6]。此类方法在准一次波数据构建过程中,伴随着准一次波有效同相轴的形成,不可避免地会出现由于不成对的一次波和多次波互相关而形成干涉噪音,进而降低了准一次波数据和后续成像结果的信噪比;第2类方法首先基于原始地震记录应用基于反馈环理论的自由界面多次波衰减方法(SRME)预测得到纯多次波记录,然后以原始地震记录作为正时扰动,将预测得到的多次波记录作为逆时扰动进行偏移成像[7-16],该类方法不需要求取准一次波,且其能够较好的保持偏移剖面的动力学特征。
通常情况下多次波逆时偏移一次成像计算相当于2次正演模拟的计算量,对于大模型数据或实际数据意味着巨大的计算消耗,早期的单卡CPU已经无法满足处理这类海量数据的要求。而随着计算机技术的发展,多卡GPU集群在处理逆时偏移时可获得几十倍的加速比。笔者基于多卡GPU集群对第2类多次波逆时偏移方法进行了研究,以期使得地震大数据体的多次波逆时偏移成像处理成为可能。
1 多次波逆时偏移成像原理
常规逆时偏移成像的原理是基于双程波动方程以震源点S的地震子波作为正时扰动进行正演模拟获得正时波场,以接收点P接受的一次波地震记录作为逆时扰动,应用有限差分等数值模拟手段进行波场延拓,最后依据成像条件对反射点rP实现成像(图1a)。多次波逆时偏移成像则是先以P点处的一次波地震记录作为正向扰动进行正演模拟获得正时波场,同时以一阶多次波记录点M1处的记录作为逆向扰动进行波场逆时延拓得到逆时波场,然后根据成像条件实现一阶多次波记录对反射点的成像;再以M1点处的一阶多次波记录作为正向扰动进行正演模拟获得正时波场,并以M2点处的二阶多次波记录作为逆向扰动进行波场逆时延拓得到逆时波场,实现二阶多次波记录对反射点rM2的成像(图1b)。
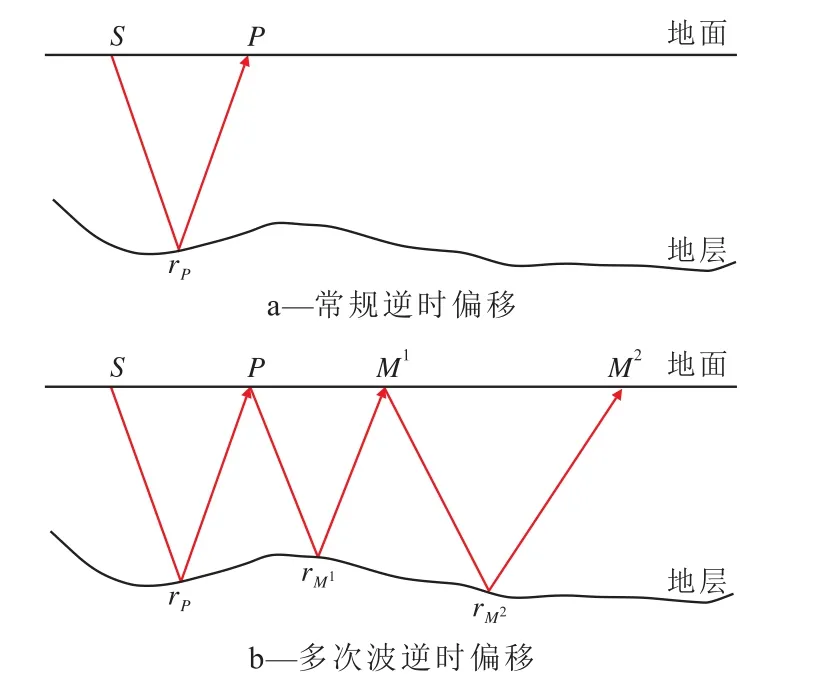
图1 不同类型逆时偏移成像原理示意Fig.1 Different typesofprinciplesof reverse timemigration imaging
多次波逆时偏移原理与常规逆时偏移相似,也是先进行正时、逆时波场的延拓,再基于成像条件提取深度成像值。但二者不同的是,常规逆时偏移的正时波场和逆时波场扰动使用的是震源子波和原始地震记录,而多次波逆时偏移的正时波场和逆时波场扰动分别为原始地震记录和基于原始地震记录预测得到的多次波记录。
2 多次波逆时偏移成像的实现
2.1基于反馈环理论的多次波预测
由多次波逆时偏移成像的原理可知,要想获得精确的成像结果需要先准确地预测出多次波记录。由于SRME可有效地预测出地震记录中的自由界面多次波记录,且对复杂构造区域的多次波和衰减都可达到较高的预测精度,因此,应用该方法进行多次波的预测。
假设地震波在地层中传播过程的表达式[17]为

其中
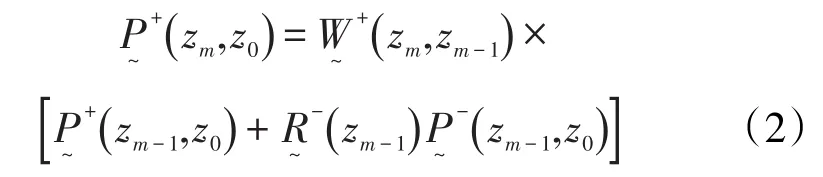
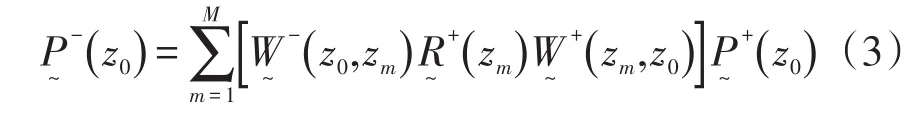
其中
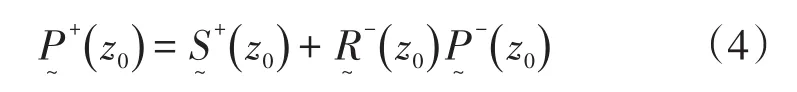
在式(3)中引入不含表层反射的地下响应矩阵,表达式为
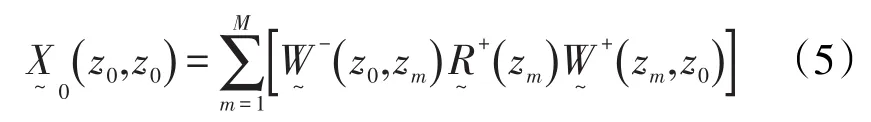
为描述检波器组合特性及虚反射的影响引入算子,则检波器接收到的地震波场可表示为
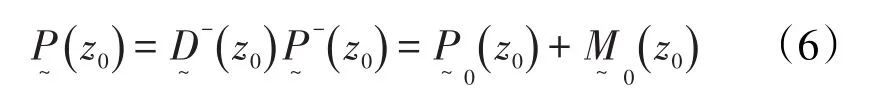
其中
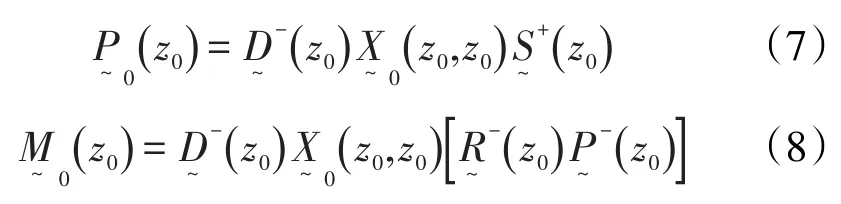
由式(7)和式(8)可以分别求得自由界面上检波器接收到的一次波和多次波。
引入一个自由界面算子,其表达式为
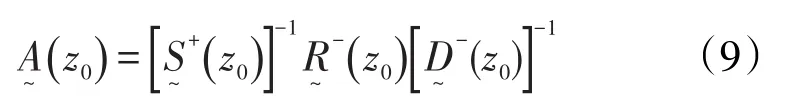
则式(6)可表示为
根据Neumann级数性质,将式(10)展开
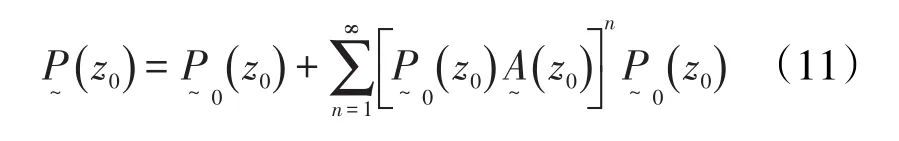
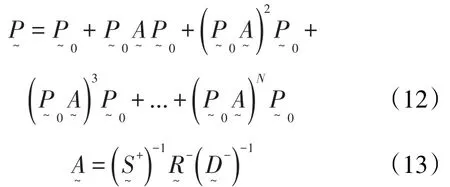
对于多次波逆时偏移成像而言,通常是以包含一次波和各阶多次波的实际记录为输入数据,应用式(12)和式(13)预测得到纯多次波记录,并以此纯多次波记录作为逆时扰动进行波场逆时延拓以得到逆时波场。
2.2多次波逆时偏移的波场延拓
多次波逆时偏移成像主要通过应用声波方程有限差分数值模拟方法进行波场的正时和逆时波场延拓。其中,地震波的传播一般可用二维声波方程来表示

式(14)通常应用有限差分数值模拟方法来求解,对于基于声波方程的正演模拟来讲,其时间二阶中心差分、空间任意2N阶精度差分格式[18]为
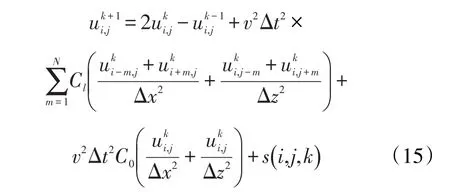
基于声波方程的波场逆时延拓的时间二阶精度、空间2N阶精度差分格式可表达为
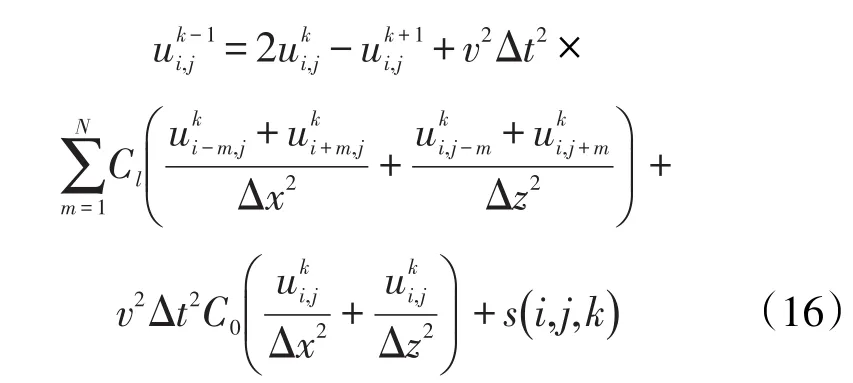
通过式(16)中的s(i,j,k)可预测得到纯多次波记录。
2.3多次波逆时偏移成像条件分析
多次波逆时偏移的最终成像需要借助成像条件来计算各个深度点上的成像值。笔者所采用互相关成像条件[8]的成像值表达式为要注意的是,和中分别包含了不同阶数的多次波正时和逆时波场,即
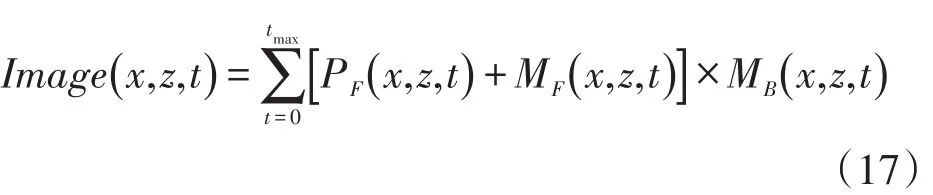

将式(18)中的表示正时波场和逆时波场中的各阶多次波代入式(17)中进一步展开可得
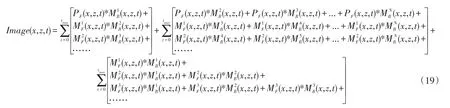
式(19)中第1项各行分别为N(N≥0)阶多次波正时波场(将一次波视为0阶多次波)与N+1阶多次波逆时波场的互相关成像值;第2项分别为N(N≥0)阶多次波正时波场与N+i(i>1)阶多次波逆时波场的互相关成像值;第3项分别为N+j(N≥1,j≥0)阶多次波正时波场与N阶多次波逆时波场的互相关成像值。Liu等[8]认为只有第1项能够对地下地质构造正确成像,而第2项会形成串扰噪音,严重影响多次波逆时偏移的深层成像精度,第3项则不能成像。
2.4基于多卡CPU集群的多次波逆时偏移成像
由于多次波逆时偏移成像的正时和逆时2次波场延拓计算量较大。相比以往的单卡CPU,GPU具有更多的计算核心和更高的带宽和访存速度[19-21],而且借助高度并行的架构可同时执行成千上万个线程,因此在处理运算密集、高度并行、控制简单的计算问题时有着单卡CPU无可比拟的优势,二者计算效率比约为50∶1。因此,基于多卡GPU集群可进一步提高多次波逆时偏移成像的计算效率和速度。根据多次波逆时偏移按炮进行偏移计算的特点,基于处理系统多点接口(MPI)先实现按炮进行任务划分,即根据参与运算的GPU卡的数目启动同样数目的处理进程,并将所有炮记录均衡地分配到各个进程,然后将每个进程与各个卡一对一进行绑定,保证每个进程对应一个卡,最后将GPU集群中各卡的计算结果归约到主进程即可实现多次波逆时偏移成像成果的输出(图2)。

图2 基于多卡GPU集群的多次波逆时偏移成像流程Fig.2 Flow chartof reverse timemigration ofmultiples based on the acceleration ofmulti-card GPU
3 多次波逆时偏移成像效果
Sigsbee2B地质模型是国际上用于地震多次波数据处理的标准模型,依据该模型建立一个长度为24 386m、深度为9 144m,横向和纵向网格步长均为7.62m,含有起伏海底界面和高陡盐丘的构造模型(图3)进行逆时偏移成像处理。

图3 基于Sigsbee2B地质模型的地震多次波数据体Fig.3 Seismic data processing ofmultiplesbased on the Sigsbee2Bgeologicalmodel
应用SRME方法预测得到该地质模型原始记录的纯多次波炮集,然后通过1个4卡的GPU工作站实现了数据体的多次波逆时偏移成像处理。为便于分析比较,将地质模型的局部构造1和2通过常规与多次波逆时偏移对成像处理的结果进行放大(图4)对比可以看出,多次波逆时偏移处理的中浅层成像清晰,构造细节分辨率较高,小高速体成像精度明显高于常规一次波逆时偏移。主要原因是因为多次波传播路径更长,覆盖范围更广,从而使得多次波逆时偏移在中浅层复杂构造的成像精度优于常规逆时偏移。
但深层界面的成像结果也显示,常规一次波逆时偏移在深层的界面清晰,构造连续性好,与原始模型基本吻合;而多次波逆时偏移的深层构造模糊,成像精度相对较低。造成二者成像精度差异的主要原因是串扰噪音的影响。因此,要使得多次波逆时偏移成像效果兼顾各层段,必须设法压制多次波逆时偏移的串扰噪音,提高其深层成像精度。

图4 Sigsbee2B地质模型不同位置逆时偏移成像结果对比Fig.4 Comparison of imaging resultsof the reverse time migration atdifferent locations in the Sigsbee2Bgeologicalmodel
4 结论
对多次波逆时偏移成像原理进行了系统剖析,结果表明,相对于一次波,多次波在地下传播的射线路径更长,覆盖的区域更广,地下照明度更加均衡,甚至能够照明到一次反射波无法到达的阴影区,可以克服常规逆时偏移成像困难的难题。
在剖析多次波逆时偏移成像原理和条件的基础上,分析多次波逆时偏移成像中的多次波预测、波场延拓等步骤的实现过程,利用Sigsbee2B地质模型应用SRME方法预测得到纯多次波炮集,实现了基于多卡GPU集群的多次波逆时偏移成像处理。处理结果显示,多次波逆时偏移中浅层成像清晰,构造分辨率高,小高速体成像精度明显高于常规一次波逆时偏移处理结果。由于受串扰噪音的影响,多次波逆时偏移结果的深层成像相对较模糊,成像精度逊色于常规一次波逆时偏移,进一步研发高精度的多次波逆时偏移方法以提高深层的成像精度将是下一步的工作重点。
[1] Whitemore N D.Iterative depth imaging by backward time propagation[C].Proceedings of the 53rd Annual International Meeting,1983:382-385.
[2] Baysal E,Kosloff D D,Sherwood JW.Reverse timemigration[J]. Geophysics,1983,48(11):1 514-1 524.
[3] Levin S A.Principle of reverse-time migration[J].Geophysics,1984,49(5):581-583.
[4] Verschuur D J,Berkhout A J.Transformingmultiples into primaries:Experience with field data[C].Expanded Abstracts of the 75th AnnualMeeting of the Society of Exploration Geophysicists,2005.
[5] Berkhout A J,Verschuur D J.Imaging ofmultiple reflections[J]. Geophysics,2006,71(4):I209-I220.
[6] 单国健.地表多次波应用研究[J].石油物探,2007,46(6):604-610. Shan Guojian.Surface-related multiplemigration[J].Geophysical Prospecting for Petroleum,2007,46(6):604-610.
[7] 郭书娟,李振春,仝兆岐,等.基于广义的炮偏移方法实现地表多次波和一次波联合成像[J].地球物理学报,2011,54(4):1 098-1 105. Guo Shujuan,Li Zhenchun,Tong Zhaoqi,et al.Joint imaging of primaries and surface-related multiples based on generalized shot-profilemigration[J].Chinese Journal of Geophysics,2011,54(4):1 098-1 105.
[8] Liu Y,Chang X,Jin D,et al.Reverse timemigration ofmultiplesfor subsaltimaging[J].Geophysics,2011,76(5):B209-B216.
[9] Wang Y,Chang X,Hu H.Simultaneous reverse timemigration of primaries and free-surface relatedmultipleswithoutmultiple prediction[J].Geophysics,2014,79(1):S1-S9.
[10]Anstey N A.The Sectional auto-correlogram and the sectional retro-correlogram[J].Geophysical Prospecting,1966,14(4):389-426.
[11]Riley DC,Claerbout JF.2-Dmultiple reflections[J].Geophysics,1976,41(4):592-620.
[12]Kennett B.The suppression of surfacemultipleson seismic records [J].Geophysical Prospecting,1979,27(3):584-600.
[13]Berkhout A J.Seismic migration:Imaging of acoustic energy by wave field extrapolation[M].Amsterdam of Holland:Elsevier,1984.
[14]Verschuur D J,BerkhoutA J,Wapenaar C.Adaptive surface-related multiple elimination[J].Geophysics,1992,57(9):1 166-1 177.
[15]Verschuur D J,Berkhout A J.Estimation ofmultiple scattering by iterative inversion,Part II:Practical aspects and examples[J]. Geophysics,1997,62(5):1 596-1 611.
[16]Dedem E V,Verschuur D J.3D surface-related multiple prediction:A sparse inversion approach[J].Geophysics,2005,70(3):V31-V43.
[17]谭军.自由界面多次波的预测与衰减[D].青岛:中国海洋大学,2011. Tan Jun.The prediction and attenuation of surface-related multiple[D].Qingdao:Ocean University ofChina,2011.
[18]刘洋,李承楚,牟永光.任意偶数阶精度有限差分法数值模拟[J].石油地球物理勘探,1998,33(1):1-10. Liu Yang,LiChengchu,Mu Yongguang.Finite-difference numerical modeling of any even-order accuracy[J].Oil Geophysical Prospecting,1998,33(1):1-10.
[19]李博,刘国峰,刘洪.地震叠前时间偏移的一种图形处理器提速实现方法[J].地球物理学报,2009,52(1):245-252. Li Bo,Liu Guofeng,Liu Hong.Amethod of using GPU to accelerate seismic pre-stack timemigration[J].Chinese Journal of Geophysics,2009,52(1):245-252.
[20]刘红伟,李博,刘洪,等.地震叠前逆时偏移高阶有限差分算法及GPU实现[J].地球物理学报,2010,53(7):1 725-1 733. Liu Hongwei,LiBo,Liu Hong,etal.Thealgorithm ofhigh order finite difference pre-stack reverse time migrationm and GPU implementation[J].Chinese Journal of Geophysics,2010,53(7):1 725-1 733.
[21]刘文卿,王宇超,雍学善,等.基于GPU/CPU叠前逆时偏移研究及应用[J].石油地球物理勘探,2012,47(5):712-716. Liu Wenqing,Wang Yuchao,Yong Xueshan,et al.Prestack reverse timemigration on GPU/CPU co-parallel computation[J]. OilGeophysical Prospecting,2012,47(5):712-716.
编辑裴磊
Reverse timem igration ofmultip lesbased on theacceleration ofmulti-card GPU
Zhu Bo1,Song Peng1,2,Li Jinshan1,2,Tan Jun1,2
(1.CollegeofMarineGeosciences,Ocean University ofChina,Qingdao City,Shandong Province,266100,China;2.Key Lab ofSubmarineGeosciencesand Prospecting Techniques,Ministry ofEducation,Ocean University ofChina,Qingdao City,Shandong Province,266100,China)
Compared to the conventional reverse timemigration(RTM),RTM ofmultiples has a higher imaging precision. Based on the analysis of the imaging principle and conditions of RTM ofmultiples,the paper studied the steps ofmultiples prediction,wave field extrapolation and so on in the imaging process of RTM ofmultiples.Then,the shotgatherswith only multipleswere obtained by applying the surface-relatedmultipleseliminationmethod based on feedback loop theory to the Sigsbee2B geologicalmodel,and the imaging processing ofRTM ofmultipleswas implemented based on the acceleration of multi-card GPU.The processing resultsshow that the imaging resultof themiddle-shallow layerobtained by RTM ofmultiples is clear,and the imaging precision of shallow structures is obviously higher than thatobtained by conventional RTM. Besides,the computationalspeed and efficiency can be improved significantly by the application ofmulti-card GPU,which makes itpossible for the imaging processingofRTM ofmultiplesbased on big data.
multiples;wave field extrapolation;reverse timemigration imaging;multi-card GPU;imaging precision
P631.4
A
1009-9603(2015)02-0060-06
2015-01-29。
朱博(1988—),男,湖北随州人,在读硕士研究生,从事地震资料数据处理研究。联系电话:13366640301,E-mail:depacino@sina.com。
李金山(1963—),男,山东昌邑人,教授级高级工程师,硕士,从事地震资料数据处理研究。联系电话:13012556790,E-mail:ljs @ouc.edu.cn。
中央高校基本科研业务费专项“多次波分阶逆时偏移成像及其GPU集群加速”(201513005)。

