基于径向基神经网络的太阳能电池缺陷检测

沈凌云，朱 明，陈小云

(1.中国科学院长春光学精密机械与物理研究所，吉林长春 130033；2.中国科学院大学，北京 100049； 3.长春理工大学电子信息工程学院，吉林长春 130022)

基于径向基神经网络的太阳能电池缺陷检测

沈凌云1，2，3，朱 明1*，陈小云1

(1.中国科学院长春光学精密机械与物理研究所，吉林长春 130033；2.中国科学院大学，北京 100049； 3.长春理工大学电子信息工程学院，吉林长春 130022)

为了检测太阳能电池的缺陷，建立了太阳能电池板的电致发光(EL)图像与其缺陷类型间的神经网络预测模型，可以对太阳能电池板不同类型缺陷进行自适应检测。首先，采用主成分分量分析(PCA)算法对电致发光(EL)图像训练样本集降维；然后，将降维后得到的数据输入神经网络预测模型进行学习，对模型的参数进行优化选取；最后，将训练好的网络对测试样本集进行仿真。仿真结果表明：在采用相同的训练样本集和测试样本集条件下，与反向传播神经网络(BPNN)相比，径向基神经网络(RBFNN)具有全局最优特性，结构简单，最高识别率达96.25%，计算时间较短，能满足在线检测的要求。

缺陷检测；反向传播神经网络；径向基神经网络；主成分分析；降维

1 引 言

随着全世界能源紧缺和日益严重的环境污染问题，人们对太阳能这种低碳环保能源的需求越来越大。目前，多晶硅由于具有高的转换效率，并且材料和工艺制造成本较低，易于产业化，占有了大部分晶体硅太阳能电池市场。多晶硅的薄片被进一步处理后，就形成一个作为太阳能发电系统基本单元的太阳能电池。一组太阳能电池组装互相连接成一个太阳能电池组件，可以提供大量电力用于各种商业应用。例如，美国AP公司的单晶硅电池组件由36片串联，其峰值功率为75 W，组件上的盖板材料为低铁钢化玻璃，四周采用铝合金边框固定，寿命长约25年，一般用于各类光伏电站。但是，太阳能电池片缺陷的存在会降低转换效率及使用年限，因此，缺陷的检测和识别对于生产质量的控制至关重要。

由于晶体硅太阳能电池片的表面缺陷用肉眼不易分辨，所以现在常用电致发光(EL)成像技术来凸显缺陷。EL技术是目前应用很广的一种太阳能电池缺陷检测方法［1］，成像只需要不到1 s的时间，并且使用CCD相机就可以拍摄，在检测仪器成本和检测效率方面都优于红外热成像(DLIT)、光感生电流(LBIC)、电感生电流(EBIC)等方法［2］。

在光伏产业中，基于机器视觉的缺陷检测方法主要集中在太阳能硅片和太阳能电池上，采用机器视觉的方法对电致发光成像批量处理能提高检测速度。德国在太阳能电池组件检测方面处于领先地位，例如，TSRAVISION公司发明的缺陷检测系统可以在线检测太阳能电池的质量，大大减少了电池组件的退货率，同时提高了组件的质量并降低了生产成本。在国内，基于机器视觉技术的太阳能电池组件缺陷检测使用还不广泛，所使用的EL红外检测设备多为离线式，只适用于抽检，做不到缺陷的在线自动识别。

目前，太阳能电池的机器视觉检测方法已有很多。Du-Ming Tsai对太阳能电池缺陷检测采用了独立主成分基图像重建的方法，识别率达到93.4%，但是由于独立主成分分析是基于所有阶的统计信息，因此其求解过于复杂［3］。姚明海采用一种基于鲁棒性的主成分分析方法，识别率接近100%，但是对输入图像预处理要求较高［4］。龚芳采用独立主成分分量和粒子群方法，能很好地区分背景和缺陷，但是没有进行缺陷类型识别统计［5］。Yih-Chih Chiou等采用区域增长法检测了微裂、污点、空洞等类型缺陷，总准确率达到99.85%，但是计算时间较长，算法速度较慢［6］。

神经网络具有很强的输入输出非线性映射能力，在模式识别领域应用很广泛，相继有很多方法应用于缺陷检测［7-8］。邓小玲等结合PCA方法将BPNN应用于柑橘黄龙病诊断，能识别出5种症状柑橘叶片，识别率达到90%以上［9］。许兆美等结合遗传算法将BPNN应用于激光铣削层质量预测，预测率达到94%以上［10］。Alexandridis A等采用RBFNN作为分类器，在9个不同的基准数据集上进行评估，结果表明该网络具有更好的逼近能力与较短的计算时间［11］。神经网络还有其他很多检测和分类器的应用，均取得了较好的效果［12-14］。

针对以上问题，本文提出融合主成分分析(PCA)改进反向传播神经网络(BPNN)方法和径向基神经网络(RBFNN)方法对太阳能电池缺陷电致发光图像进行处理，主要包括图像采集、PCA特征提取降维、神经网络分类训练、预测输出等部分。研究结果表明，PCA方法能降低输入图像维数，有效地提取图像特征，简化神经网络结构及计算量；RBFNN比BPNN的参数更易于调节，且能获得更高的识别率及更短的计算时间。

2 本文提出的方法

EL检测原理与检测系统在文献［1］中有详细的描述。本文采用该文献中的方法对太阳能电池片的EL图像进行采集。图1(a)、(b)、(c)分别表示由CCD采集的一块大小为125 bits×125 bits的虚焊缺陷图像、微裂缺陷图像和断指缺陷图像。图1(d)是无缺陷太阳能电池组图像，它包含36(6×6)块大小为125 bits×125 bits的太阳能电池片图像。

本文提出融合主成分分析(PCA)改进反向传播神经网络(BPNN)方法和径向基神经网络(RBFNN)方法对太阳能电池缺陷电致发光图像进行处理，主要包括图像采集、PCA特征提取降维、神经网络分类训练、预测输出等部分，如图2所示。

图1 太阳能电池板EL图像。(a)虚焊图像；(b)微裂图像；(c)断指图像；(d)无缺陷图像。Fig.1 EL images of solar panels.(a)Rosin joint.(b)Microcrack.(c)Gate electrode broken.(d)No defect.

图2 基于神经网络的太阳能电池缺陷检测示意图Fig.2 Detection of defect on solar panels based on NN

2.1 PCA处理输入数据

当BPNN和RBFNN的输入是太阳能电池板缺陷图像集时，图像是以向量的形式表示。向量维数太大将不利于网络的计算。我们采用主成分分量分析(PCA)算法［15］来提取该向量的主要特征分量，既不损失重要信息又能减少网络的计算量。

PCA是基于协方差矩阵将样本数据投影到一个新的空间中，那么表示该样本数据就只需要该样本数据最大的一个线性无关组的特征值对应的空间坐标即可。将特征值从大到小排列，取较大特征值对应的分量就称为主成分分量。通过这种由高维数据空间向低维数据空间投影的方法，可以将原始的高维数据压缩到低维。

假设数据矩阵Xn×p由样本图像组成，n是样本数，p是样本图像的大小。若Xn×p的每一行代表一幅样本图像，则Xn×p的PCA降维矩阵求解步骤如下：

(1)求Xn×p的平均值。设样本图像分别为X1…Xn，则平均值定义如下：

(2)形成一个新矩阵M。从X1…Xn中减去如下所示：

则新矩阵 M=(Φ1Φ2…Φn)，求 M的协方差矩阵：

(3)通过公式(4)、(5)求特征值λ及特征矢量U：

保留k个较大特征矢量形成Y：

PCA降维后的矩阵Y是神经网络的输入矩阵。

2.2 创建BPNN模型和RBFNN模型

太阳能电池缺陷种类很多，不同缺陷类型图像具有不同特征。对太阳能电池缺陷图像求其主成分分量作为BPNN的输入，缺陷的分类作为输出，输入层有k个神经元(降维后主成分分量个数)，输出层有1个神经元(缺陷的分类向量)。隐层的节点数可以凭经验多次实验确定，也可以设计一个隐含层数目可变的BPNN。通过误差对比，选择在给定对比次数内误差最小所对应的隐含层神经元数目，从而确定BPNN的结构。一般来说，3层BPNN就能以任意的精度逼近任意的连续函数［16］。本论文选择 3层BPNN，结构为k-m-1，m为隐含层节点数。为了使网络训练时不发生“过拟合”现象，设计合理BPNN模型的过程是一个不断调整参数对比结果的过程。

确定BPNN结构后，就可以对该网络进行训练。训练函数采用Levenberg-Marquardt函数，隐含层神经元传递函数为S型正切函数tansig，输出层神经元函数为纯线性函数purelin。调用格式：net= newff(Y，T，［m，1］，｛‘tansig’，‘purelin’｝，‘trainlm’)；Y为神经网络的输入矩阵向量(PCA降维后的矩阵向量)，T为神经网络的输出矩阵向量。

Matlab自带4种主要的函数来设计RBFNN：newrbe，newrb，newgrnn，newpnn。本文用相同的训练样本集和测试样本集创建和测试了这4种网络，其中，用newgrnn创建的网络识别率最高，因此选用广义回归神经网络newgrnn来创建RBFNN：

(1)隐含层径向基神经元层数目等于输入样本数，其权值等于输入矩阵向量的转置，阈值为：

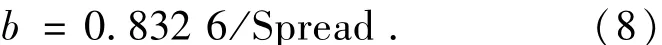
(2)输出层线性神经元层，以隐含层神经元的输出作为该层的输入，权值为输出矩阵向量T，无阈值向量。

调用格式：net=newgrnn(Y，T，Spread)；Y为神经网络的输入矩阵向量(PCA降维后的矩阵向量)，T为神经网络的输出矩阵向量，Spread为径向基函数的扩展速度。

2.3 太阳能电池缺陷的检测算法

(1)数据映射。取每种类型缺陷图像的60%和40%分别作为BPNN和RBFNN的训练样本集和测试样本集。将样本集中每张图片变成矩阵中的一列，形成一个矩阵，采用2.1节中的方法对该矩阵进行PCA降维后的矩阵作为BPNN和RBFNN的输入。将虚焊、微裂、断指和无缺陷4种不同类型图像分别标记为1，2，3，4，作为网络期望输出T。

(2)数据归一化。将输入输出矩阵向量归一化为［-1，1］，利于神经网络的计算。

(3)分别调用2.2节中创建的BPNN和RBFNN，设置网络参数，利用训练样本集先对网络训练，然后将训练好的网络对测试样本集进行仿真，并对仿真结果进行反归一化。

(4)最后将仿真预测输出分别和图像1，2，3，4比较，差值的绝对值小于阈值0.5认为预测正确。阈值是根据网络的期望输出选择的，以能正确区分不同缺陷类型为宜。识别率定义为正确识别的数量和样本数的比值。

3 实验内容与结果分析

为了验证本文方法的有效性，我们通过CCD图像采集系统采集了1 000张太阳能电池板EL图片，包括250张虚焊样本、250张微裂样本、250张断指样本、250张无缺陷样本，大小为125 bits× 125 bits。我们利用图片组成的样本数据集进行了大量的实验，将每种类型缺陷图像的60%和40%分别作为BPNN和RBFNN的训练样本集和测试样本集。

算法测试硬件平台为Intel i5 750、主频2.66 GHz的CPU，4 G内存的PC机，编译环境为Matlab R2012b。

表1 n=1 000时的PCA-BPNN识别率Table 1 Accuracy of PCA-BPNN

图3 不同样本集数下的PCA-BPNN的识别率Fig.3 Accuracy of PCA-BPNN on different number of sample sets

由于样本图像数据较大，需采用2.1节中的PCA算法进行降维处理。对样本图像集降维后，得到神经网络的输入矩阵。但是，随着样本数的增加，占有主要信息的主成分维数也在增加。因此，分别采用占有主要信息60%～90%的图像作为BPNN的输入，对应的降维后的主成分维数k为BPNN输入层节点数。由于BPNN的结果每次都不同，所以运行50次，保存识别率最高的网络。

图3是在不同样本集数下的PCA-BPNN的最高识别率。其中，样本数n=1 000时的PCA-BPNN识别率如表1所示。同时网络参数设置也列在表1中。隐含层中的最佳节点数是采用经验公式所得［17］。从图3和表1中可以看出，当维数降至20维(占主要信息70%)、总样本数为1 000(测试样本400)时，4种类型总的最高识别率为93.5%。

在相同的训练样本集和测试样本集上，采用与BPNN同样的输入和输出，在不同样本集数下，PCA-RBFNN的最高识别率如图4所示。其中，样本数n=1 000时的PCA-RBFNN识别率如表2所示。参数Spread的设置也列在表2中，首先设定Spread为1，然后以10倍的间隔速度递减。从图4和表2中可以看出，样本数为1 000(测试样本400)时，PCA维数降到15(占主要信息65%)，总的最高识别率为96.25%。

表2 n=1 000时的PCA-RBFNN识别率Table 2 Accuracy of PCA-RBFNN

图4 不同样本集数下的PCA-RBFNN的识别率Fig.4 Accuracy of PCA-RBFNN on different number of sample sets

两种网络的测试样本集最高识别率对比分别如图5和表3所示。图5(a)、(b)分别为采用PCA-BPNN与PCA-RBFNN方法时测试样本集中的4种缺陷样本图像的期望值与预测值。表3列出了两种方法的具体识别结果。从表3可以看出，两种方法对虚焊缺陷识别率均较高，分别为99%和100%；微裂缺陷识别率较低，分别为89%和92%。这是因为虚焊缺陷面积较大，颜色较深具有显著特点；而微裂缺陷面积较小，与背景对比不强烈，导致错误分类。

图5 n=1 000(测试集为400)时，PCA-BPNN(a)与PCA-RBFNN(b)的识别率。Fig.5 Accuracy of PCA-BPNN(a)and PCA-RBFNN(b) on n=1 000 samples set

表3 PCA-BPNN和PCA-RBFNN识别率的对比Table 3 Comparison between PCA-BPNN and PCA-RBFNN

采用本文提出的BPNN和RBFNN方法处理一幅750×750大小的图像大约分别需要1.8 s和0.1 s，PCA降维的时间大约为0.02 s。将上述两种方法与FCM［18］及ICA［3］方法进行比较，结果如表4所示。可以看出，RBFNN方法具有较高的识别率和较短的计算时间，更适合于在线检测。

表4 4种方法识别率及计算时间比较Table 4 Accuracy and computational time of fourmethods

4 结 论

根据现代太阳能电池板高质量的要求，提出了表面缺陷的PCA-RBFNN检测方法，并与PCABPNN在网络构建、参数设置、识别结果及计算时间方面进行了对比。结果表明，RBFNN具有较高的识别率和较短的计算时间，更适宜在线检测。BPNN和RBFNN随着样本数的增加其识别率也会相应增加，所以样本数据库的完善会提高神经网络识别率。

［1］Fuyuki T，Kitiyanan A.Photographic diagnosis of crystalline silicon solar cells utilizing electroluminescence［J］.Appl. Phys.A，2009，96:189-196.

［2］Li Y H，Pan M，Pang A S.The application of electroluminescence imaging to detection the hidden defects in silicon solar cells［J］.Chin.J.Lumin.(发光学报)，2011，32(4):378-382(in Chinese).

［3］TsaiDM，Wu SC，Chiu W Y.Automatic visual inspection of solarmodules using independent componentanalysis［C］// Proceedings of The 14th Asia Pacific Industrial Engineering and Management Science Conference，Cebu:IEEE，2013.

［4］Yao M H，Li J，Wang X B.Solar cells surface defects detection using RPCA method［J］.Chin.J.Comput.(计算机学报)，2013，36(9):1943-1952(in Chinese).

［5］Gong F，Zhang XW，Sun H.Detection system for solarmodule surface defects based on constrained ICA model and PSO method［J］.Acta Optica Sinica(光学学报)，2012，32(4):1-9(in Chinese).

［6］Chiou Y C，Liu J Z，Liang Y T.Micro crack detection of multi-crystalline silicon solar wafer using machine vision techniques［J］.Sens.Rev.，2011，31:154-165.

［7］Jin J，Zhang ZG，Wang Z，etal.Temperature errors compensation for digital closed-loop fiber optic gyroscope using RBF neural networks［J］.Opt.Precision Eng.(光学精密工程)，2008，16(2):235-240(in Chinese).

［8］Zeng L，He H J，Zhang ZB.Comparison inspection between ICT images&CADmodelbased on edge extracting by neural networks［J］.Opt.Precision Eng.(光学精密工程)，2011，19(10):2533-2540(in Chinese).

［9］Deng X L，Cheng K，Wu W B.Detection of citrus huanglongbing based on principal componentanalysis and back propagation neural network［J］.Acta Photon.Sinica(光子学报)，2014，43(4):1-7(in Chinese).

［10］Xu ZM，Zhou JZ，Huang S，et al.Quality prediction of lasermilling based on optimized back propagation networks by genetic algorithms［J］.Chin.J.Lasers(中国激光)，2013，40(6):1-8(in Chinese).

［11］Alexandridis A，Chondrodima E.Amedical diagnostic tool based on radialbasis function classifiers and evolutionary simulated annealing［J］.J.Biomed.Inform.，2014，49(1):61-72

［12］Lu C，Zhu Z，Gu X.An intelligent system for lung cancer diagnosis using a new genetic algorithm based feature selection method［J］.J.Med.Syst.，2014，38(9):97-105

［13］Tong D L，Schierz A C.Hybrid genetic algorithm-neural network:Feature extraction for unpreprocessed microarray data［J］.Artif.Intell.Med.，2011，53(1):47-56.

［14］Babu G S，Suresh S.Sequential projection-based metacognitive learning in a radial basis function network for classification problems［J］.IEEE Trans.Neur.Network Learning Syst.，2013，24(2):194-206.

［15］Ghosh-Dastidar S，Adeli H，Dadmehr N.Principal component analysis-enhanced cosine radial basis function neural network for robust epilepsy and seizure detection［J］.IEEE Trans.Biomed.Eng.，2008，55(2):512-518.

［16］Cybenko G.Approximation by superpositions of a sigmoidal function［J］.Mathematicsof Control，Signals，and Systems，1989，2(4):303-314.

［17］Xia KW，Li C B，Shen JY.An optimizational algorithm on the number of hidden layermodels in feed-forward neural network［J］.Comput.Sci.，2005，32(10):143-145.

［18］Li G N，Tan Q C，Zhang K，et al.Solar cells defect detection in electroluminescence images［J］.Chin.J.Lumin.(发光学报)，2013，34(10):1400-1407(in Chinese).

Solar Panels Defect Detection Based on Radial Basis Function Neural Network

SHEN Ling-yun1，2，3，ZHU Ming1*，CHEN Xiao-yun1
(1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.University of Chinese Academy of Sciences，Beijing 100049，China；3.School of Electronics and Information Engineering，Changchun University of Science and Technology，Changchun 130022，China) *Corresponding Author，E-mail：zhu-mingca@163.com

In order to detect the defect on solar panels and improve the conversion efficiency，two neural network modelswere established between solar panels electroluminescence(EL)images and defect types，which can detect different types of defects on solar panels adaptively.Firstly，the dimensions of EL images training samples set were reduced by using principal component analysis (PCA).Then，EL images training samples set after dimension reduction was put into the neural networks for training.Finally，the testing samples setwas simulated by the trained network through choosing the best parameters.Compared with BPNN，RBFNN has the advantages of global optimization characteristics and simple structure，which leads to the highest accuracy rate of 96.25%and shorter computational time.The experiment results show that RBFNN can meet the requirements of online detection.

defect detection；back propagation neural network(BPNN)；radial basis function neural network (RBFNN)；principal component analysis(PCA)；dimension reduction

国家自然科学基金(61203242)；中国科学院二期创新工程基金(C50T0P2)资助项目

TP394.1；TH691.9

A

10.3788/fgxb20153601.0099

book=105,ebook=108

1000-7032(2015)01-0099-07

2014-08-22；

2014-10-19

沈凌云(1979-)，女，湖北钟祥人，博士研究生，2007年于长春理工大学获得硕士学位，主要从事机器视觉、视频图像处理及应用等方面的研究。E-mail：shenshly@gmail.com

朱明(1964-)，男，江西南昌人，研究员，博士生导师，1991年于中国科学院长春光学精密机械研究所获得硕士学位，主要从事数字图像处理、光电成像计算、电视跟踪和自动目标识别技术等方面的研究。E-mail：zhu-mingca@163.com