热光耦合作用下的光纤传输特性

周 吉，韩 冰，韩哈斯敖其尔，马 宇*

(1.哈尔滨工业大学能源学院，黑龙江哈尔滨 150001；2.中国科学院长春光学精密机械与物理研究所，吉林长春 130033)

热光耦合作用下的光纤传输特性

周 吉1，韩 冰2，韩哈斯敖其尔2，马 宇1*

(1.哈尔滨工业大学能源学院，黑龙江哈尔滨 150001；2.中国科学院长春光学精密机械与物理研究所，吉林长春 130033)

通过求解电磁波束包络方程和能量方程的耦合方程组，考虑温度对材料介电系数的影响及传输损耗产热的耦合作用，求解了复合热边界条件下光纤的基模态传输和损耗问题。研究表明：随着纤芯半径的增大，电场强度、能量耗散密度减小，传播常数增大；环境温度降低、对流换热系数增大和表面发射率升高都会使得传播常数减小，电场强度、能量耗散密度增大；能量耗散密度和电场强度随截面曲率的变化并不是线性的，还受到其他因素的共同作用。

光纤基模态；传播常数；能量耗散密度；热光耦合

1 引 言

光纤波导在无线电通讯、雷达、导航等无线电领域有着广泛的应用，由于其传输衰减较小，频带很宽，近年来已经逐渐取代电信号传输成为一种信号传输的主要工具。已有研究证明温度是影响光束传输质量的一个重要因素［1-2］，而光纤作为光传输的一种主要媒介，随着对其大容量传输和精确传输要求的提高，温度对光纤传输的稳定性和精确度的影响也日益受到重视。Aleksandrov等［3］提出了针对光纤耦合激光器模块的光纤末端的温度控制系统，从而保证在600～1 100℃温度范围内误差小于1%。Dong等［4］指出光纤激光器在高功率状态下会存在模式不稳定性，限制单模光纤的输出功率的比例，此时热光耦合作用将显著凸现。Heimann等［5］指出，在操作过程中热工作条件会严重影响光纤陀螺仪的光纤线圈的精度和稳定性，尤其是温度梯度对光纤陀螺仪的精确度有很大的负面影响。Filiche等［6］考虑了热对光纤吸收特性的影响，提出利用光子晶体光纤的吸收光谱研究包含在细胞中的水发生的温度变化，并设计出一种新型的温度检测器。此外，人们也研究了热对光纤传输性能的影响，如Lee等［7］研究了依赖压力的层间接触热阻对双层涂料光纤中瞬态局部严重挠曲损耗和光纤折射率的影响效果，Yang等［8-9］研究了带有层间热阻的单层覆盖光纤的瞬态热负荷导致的挠曲损耗和折射率改变。对于光纤传输模式也已有了很多研究［10-12］，但通常只考虑了环境变化对光学传输模式或传输损耗的单向的影响，而实际上当光传输模式或传输损耗发生改变时，也可能对光纤自身属性产生影响，因为传输损耗会转化为热使得光纤工作温度改变，而温度将影响光纤的物理性质。

Chu等［13］将多重镀膜光纤充当瞬态热负荷作用，采用基于反向算法的共轭梯度法来估算不同环境温度下未知的随时间变化的对流换热因子，通过读出光纤表面的瞬态温度，反演获得对流换热因子的值。研究结果表明，光纤在不同的传输状态时其温度是有所不同的。张顺德等［14］研究了制造光纤纤芯的一种重要材料——石英的折射率和吸收系数随温度的变化。结果表明：当纤芯温度改变时，其传输模式和传输损耗可能发生改变，而这又会进一步诱发温度场的变化。此外，光纤和环境的换热也会影响到光纤的实际运行温度。这是一种典型的热光双向耦合过程，针对这一过程的研究有利于我们更好地了解光纤在实际应用中的真实传输模式和损耗情况。基于此，本文研究了辐射-对流耦合换热边界下的光纤中的光传输模式和损耗情况。

本文采用有限元方法来求解束包络的电磁波动方程和能量方程的耦合方程组，对光纤光传输过程开展模式分析，在同时考虑光纤与外界环境的对流换热和辐射换热的情况下，模拟获得了光纤波导中的场强、损耗及温度场分布，对不同入射功率、不同纤芯半径、不同热边界条件以及不同光纤截面形状的光传输过程进行了讨论。通过分析比较各个物理量的影响大小，获得了基模态电场场强、能量损耗密度和传播常数的变化规律。研究结果可为拓展光纤信号传输和大功率光纤激光器在复杂场合的应用提供一定的参考。

2 研究方法

采取电磁波束包络模式方法来求解光纤中的场分布。束包络法的基本原理如图1所示。

图1 束包络法的基本原理Fig.1 Basic principle of beam envelopemethod

电场和电场包络线的关系为

其中k1是电场包络线的波矢量。在计算电场E时，传统的方法必须取足够的单元，但是对于束包络问题而言，电场包络线的波动性远远小于电场本身的波动性，因此在计算时只需要计算电场包络线。在图1中，包络线的网格尺寸远远大于电场的网格尺寸，因此相对于全波求解的方法，采用包络线的方法进行计算时其网格数量可以大大减少，从而可以减少模型的自由度，减少计算资源和计算时间。

将方程(1)代入Helmholtz方程：

可得

方程(3)是方程(2)的一种准确推导，仍然是一种波动方程。束包络的方法是一种精确计算，并不包含近似手段。波矢大小通过端口和边界模式分析得到具体的数值，然后可以得出整个计算空间中的场分布。

光纤传输过程中不可避免会存在损耗。本文主要考虑电磁能量的损耗，将损耗的能量转化为一个热源导入热传输模型中，主要由两部分组成：

其中第一项Qrh为电阻损耗：

而第二项Qml为磁性损耗：

光纤中的温度分布通过求解能量方程(7)和边界条件(8)获得。式(7)中，Q为内热源。对于纤芯，Q=Qc；对于包层，Q=0。式(8)中，q为对环境释放的热量。式中Tamb为环境温度，k为热导率，cp为比热，ε为表面发射率。

3 模型建立与求解

图2 光纤的物理模型示意图Fig.2 Schematic diagram of optical fiber's physicalmodel

图3 各个方向上的电场强度和传输损耗在截面处的分布。(a)X方向电场强度分量；(b)Y方向电场强度分量；(c)Z方向电场强度分量；(d)电场模值；(e)能量耗散密度；(f)温度场。Fig.3 Cross-sectional electric-field intensity and transmission energy loss distribution.(a)X-direction electric field intensity. (b)Y-direction electric field intensity.(c)Z-direction electric field intensity.(d)Electric field norm.(e)Total power dissipation density.(f)Temperature field.

物理模型如图2所示。光纤由包层和纤芯组成，其中包层折射率为1.1，纤芯折射率大于包层，其折射率和吸收系数根据文献［14］的结果插值获得。纤芯热导率为1.1 W/(m·K)，比热为480 J/(kg·K)；包层热导率为1.38W/(m·K)，比热为703W/(m·K)。在包层外镀有一发射率为0.9的膜，镀层的厚度忽略不计。无特别声明时，光纤长为10 mm，纤芯半径为8μm，包层半径为40μm。光在光纤中沿着y轴方向传输，输入端功率为0.1 W，包层与外界对流换热系数为10 W/(m2·K)，外界环境温度为273.15 K。网格划分时，对纤芯处网格进行加密。由于采用了束包络法，所以无需再以波长的1/5作为网格单元的特征尺度，而是可以采取更大的网格特征尺度。本文中先在端面上采用三角形网格划分，然后沿着长度方向进行扫掠而成，网格总数为133 200个。经过网格无关性检验发现，在此基础上继续增多计算网格，计算结果保持不变。

本文基于有限元方法求解束包络方程(3)。通过给初始温度场(初始温度=环境温度)时的纤芯的折射率和吸收系数赋值，获得光纤内的电磁场分布和损耗分布。将电磁能的损耗作为产热源项导入能量方程中，计算获得温度场的全局分布。以此为基础更新介电系数的值，再次求解获得电磁场分布，依次循环，最终当两次计算获得的同一位置温差小于0.1 K时，认为计算已经达到了收敛。图3显示了当端面输入功率为0.1 W、对流换热系数为10 W/(m2·K)、包层外镀层发射率为0.9时，光纤中心截面处X、Y、Z方向的电场强度分布、总的电场模分布、能量耗散密度分布和温度分布。

4 结果与讨论

针对频率为3.0E14/1.35 Hz的光在光纤中的传输特性，本文分别研究了不同端口入射功率、不同光纤截面形状、不同纤芯尺度大小和不同温度场(含不同环境温度、不同对流换热系数、不同镀层发射率)情况下的光传输特性，重点分析了基模态纤芯中心电场强度、传输损耗、光纤温度和传播常数的变化，总结出以上变化与影响因素之间的关系。

4.1 输入功率的影响

文献［14］的研究表明：当频率为3.0E14/1.35 Hz时，温度为307 K时石英复折射率实部为1.22，虚部为0.235E-6；而当温度为407 K时，复折射率实部为1.3，虚部为0.222 25E-6。可以看出，在307～407 K的温度范围内，折射率实部随着温度的升高而增大，而虚部随着温度的升高而减小。图4所示为纤芯中心温度和传播常数随着入射光功率的变化，可以看出温度和传播常数均随着功率的增加而增大。而图5所示为能量耗散密度和电场强度大小随着入射光功率的变化关系，可以看出能量耗散和电场强度均随着入射功率的增大而增加。造成以上现象的主要原因是因为入射功率增大导致输入的电磁能量增加，因此电场强度增大，转化成热量的部分也随之增大，使得光纤的温度升高，能量耗散密度也增大。虽然吸收系数在温度升高时会略有下降［14］，但其数值改变很小，造成的影响完全无法与入射光功率的改变相比，导致光纤的温度上升，而温度上升又导致折射率增大，由于传输频率不变因此光波相速度减小，从而使得传输波长变短，传播常数变大。

图4 纤芯中心温度和传播常数随入射功率的变化Fig.4 Fiber core center temperature and propagation constant vs.incident power

图5 能量耗散密度和电场强度随入射功率的变化Fig.5 Energy dissipation density and electric-field intensity vs.incident power

4.2 纤芯尺寸的影响

图6所示为温度和传播常数随纤芯半径的变化关系，可以看出随着纤芯半径的增大，纤芯中心处温度会略微降低，而光纤的传播常数会有所增大。图7所示为能量耗散密度和电场强度随纤芯半径的变化关系，可以看出随着纤芯半径的增大，能量耗散密度和纤芯中心处的电场强度均有所下降。造成上述现象的主要原因是在光输入功率不变的情况下，半径增大会导致纤芯体积增大，造成同样能量的分布更加分散。另外，由于传播常数，其中k0就是一个介质中的波的波矢大小，由于此时温度变化很小，所以介质波矢k0的变化也可忽略不计。而kx为基模态的横向波矢，增大光纤的半径等于减小基模态的横向波矢kx，因此传播常数会随纤芯半径的增大而增大。

图6 纤芯中心温度和传播常数随纤芯半径的变化Fig.6 Fiber core center temperature and propagation constant vs.fiber core radius

图7 能量耗散密度和电场强度随纤芯半径的变化Fig.7 Energy dissipation density and electric field intensity vs.fiber core radius

4.3 温度场的影响

4.3.1 环境温度的影响

图8所示为能量耗散密度和电场强度随环境温度的变化，从图中可以看出能量耗散密度和电场强度随着环境温度的升高而减小。而图9所示为纤芯温度和光纤传播常数随环境温度的变化，可以看出温度和传播常数均随环境温度的升高而增大。以上现象的产生主要是因为环境温度的升高减弱了光纤对外的散热能力，导致纤芯温度也升高。这一方面导致吸收系数降低，使能量损失减少，能量耗散密度降低；另一方面导致折射率升高，相应相速度减小，稳态时的传输波长变短，因此传播常数增大。而折射率升高也同时意味着介电系数的增大，纤芯的电阻减小，因此在相同距离内电势能的降低减少，电场强度的模值降低。

图8 纤芯中心温度和传播常数随环境温度的变化Fig.8 Fiber core center temperature and propagation constant vs.ambient temperature

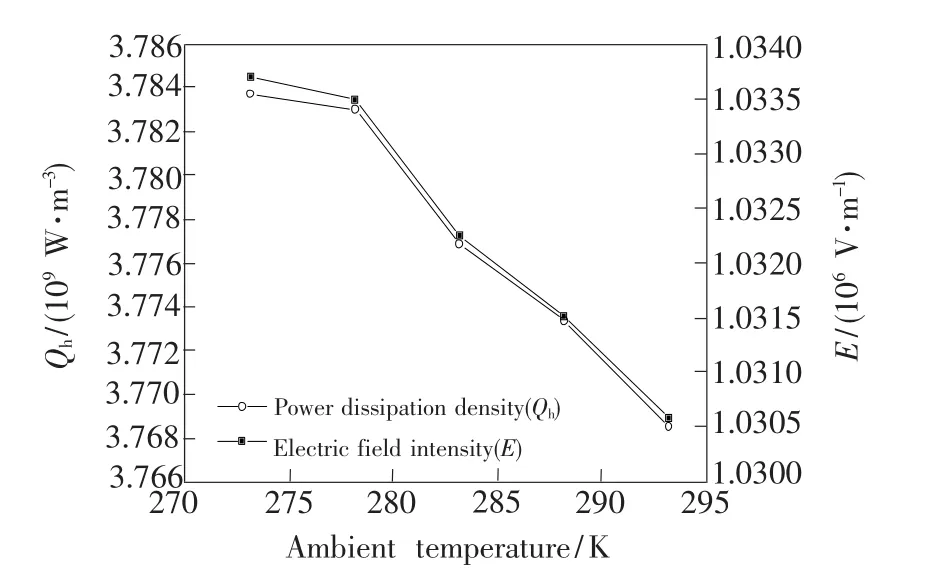
图9 能量耗散密度和电场强度随环境温度的变化Fig.9 Energy dissipation density and electric-field intensity vs.ambient temperature

4.3.2 对流换热系数的影响

图10 纤芯中心温度和传播常数随对流换热系数的变化Fig.10 Fiber core center temperature and propagation constant vs.convective heat transfer coefficient

图10所示为纤芯温度和光纤传播常数随着对流换热系数的变化，可以看出随着对流换热系数的增大，纤芯温度和光纤传播常数均有所减小。图11所示为能量耗散密度和电场强度随对流换热系数的变化，可以看出能量耗散密度和电场强度随着对流换热系数的增大而增大。造成以上现象的原因主要是对流换热系数的增大加强了光纤的散热能力，导致光纤温度下降，从而导致折射率减小，吸收系数增大。

图11 能量耗散密度和电场强度随对流换热系数的变化Fig.11 Energy dissipation density and electric-field intensity vs.convective heat transfer coefficient

4.3.3 表面发射率的影响

图12所示为纤芯温度和光纤传播常数随着包层外镀层发射率的变化，可以看出随着发射率的增加，纤芯温度和光纤传播常数均有所减小。图13所示为能量耗散密度和电场强度值随镀层发射率的变化，可以看出能量耗散系数和电场强度值均随镀层发射率的增大而增大。从数值上可以看出，发射率改变的影响远小于对流换热系数的改变，由此可认为相比于对流换热而言，辐射换热对光纤模式传输只有微弱的影响。

图12 纤芯中心温度和传播常数随镀层发射率的变化Fig.12 Fiber core center temperature and propagation constant vs.coating emissivity coefficient

图13 能量耗散密度和电场强度随镀层发射率的变化Fig.13 Energy dissipation density and electric-field intensity vs.coating emissivity coefficient

4.4 截面形状的影响

表1给出了截面面积相等、长短轴之比不同的圆形和椭圆形光纤中的温度、传播常数、能量耗散密度和电场强度随着截面形状的变化，其中S为椭圆短轴长度，L为椭圆长轴长度。

从表1中可以看出，随着截面的形状由圆逐渐变为椭圆，光纤与外界换热的表面积增大，纤芯的温度逐渐降低，传播常数逐渐减小。计算发现，能量耗散密度和电场强度此时并没有像温度和传播常数一样呈线性变化规律，而是先略微减小，再逐渐增大。当S/L=0.64时，能量耗散密度和电场强度均为最小。这是因为此时电场强度和能量耗散不再只随折射率和吸收系数的改变而改变，同时也因为光纤形状的改变而发生变化，最终得到的数值是温度和光纤形状共同作用的结果。

表1 不同截面形状光纤的参数变化Table 1 Parameter values in case of different cross-section shapes

5 结 论

通过有限元法求解经过束包络变换的Helmholtz方程和能量方程的耦合方程组，在同时考虑光纤内部传输损耗和外部对流换热、辐射换热的复合热边界条件下，针对光纤基模态传输时的电场强度、能量耗散密度、温度和传播常数进行了讨论，研究了不同输入功率、不同纤芯尺寸、不同环境温度、不同对流换热系数、不同外表面发射率以及不同截面形状对光纤参数的影响。研究结果表明：随着入射光功率的增大，温度、传播常数、电场强度和能量耗散密度均增大；随着纤芯半径的增大，温度、电场强度、能量耗散密度均减小，传播常数增大；环境温度降低、对流换热系数增大和表面发射率升高都会使温度、传播常数减小，而电场强度、能量耗散密度增大；光纤形状的改变会和折射率、吸收系数一起改变能量耗散密度和电场强度。本文的研究结果对拓展光纤信号传输和大功率光纤激光器在复杂场合的应用具有一定意义。

［1］Liu J，Li SM，Zhao J，et al.Combined influence ofmirror thermal deformation and blowing on beam propagation［J］. Opt.Precision Eng.(光学精密工程)，2014，22(8):2032-2038(in Chinese).

［2］Wu X Y，Zhang LC，ShiG.Optical-thermal and optical-acoustics detecting techniques applied for the characterizations of high performance optical thin films［J］.Chin.Opt.(中国光学)，2014，7(5):701-711(in Chinese).

［3］Aleksandrov SE，Gavrilov G A，Sotnikova G，et al.Optical-fiber-tip temperature control system for fiber-coupled laser modules in medical equipment［J］.Semiconductors，2014，48(1):139-134.

［4］Dong L.Stimulated thermal Rayleigh scattering in optical fibers［J］.Opt.Express，2013，21(3):2642-2656.

［5］Heimann M，Liesegang M，Arndt-Staufenbiel N，et al.Optical system components for navigation grade fiber optic gyroscopes［J］.SPIE，2013，8899:88991A-1-9.

［6］Filiche S，Battinilli E，Wynne R.Microstructured optical fiber monitor for cryogenic applications［J］.SPIE，2013，8693:86930S-1-11.

［7］Lee H L，Sun SH，Chang W J，et al.Transient thermal loading induced optical effects in tightly jacketed double-coated optical fibers with interlayer thermal contact resistance［J］.Opt.Commun.，2011，285(4):447-452.

［8］Yang Y C，Lee H L.Transient thermal loading induced optical effects in single-coated optical fiberswith interlayer thermal resistance［J］.Opt.Fiber Technol.，2008，14(2):143-148.

［9］Yang Y C.Estimation of thermal contact resistance and thermally induced optical effects in single-coated optical fibers［J］.Opt.Commun.，2007，278(1):81-89.

［10］Tan X F，Liu X L，ZhaoW，et al.Modal characteristics analysis of a doubly clad optical fiber with semi-weakly guiding approximation［J］.Opt.Commun.，2013，294C:148-155.

［11］Li Y R，Chen M Y.Analysis in largemode area optical fiber with two-ring holes［J］.Acta Photon.Sinica(光子学报)，2012，41(12):1412-1415(in Chinese)

［12］Toupin P，Brilland L，Troles J，etal.Small core Ge-As-Semicrostructured optical fiberwith single-mode propagation and low optical losses［J］.Opt.Mater.Express，2012，2(10):1359-1366.

［13］Chu SS，ChangW J.Inverse-estimated transient thermal responses ofmulticoated optical fiber under time-dependentheat transfer environments［J］.Opt.Eng.，2007，46(1):018001-1-5.

［14］Zhang SD，Xia X L，DaiG L，et al.Experimental investigation on spectral thermal radiation properties of optical quartz at high-temperature［J］.J.Eng.Thermophys.(工程热物理学报)，2012，33(6):1032-1034(in Chinese).

Transm ission Charactertistics of Optical Fiber Under Coupled Thermal-optical Effects

ZHOU Ji1，HAN Bing2，HAN-Hasiaoqier2，MA Yu1*
(1.School of Energy Science and Engineering，Harbin Institute of Technology，Harbin 150001，China；2.Changchun Institute of Optics，Fine Mechanicsand Physics，Chinese Academy of Sciences，Changchun 130033，China) *Corresponding Author，E-mail：mayu@hit.edu.cn

The optical fiber's base-mode transmission and energy loss under integrated thermal boundary conditionswere analyzed by using a coupling equation set composed of an electromagnetic beam envelope equation and an energy equation.The impact of the temperature on thematerial's dielectric coefficient as well as the heat generation induced by energy loss during transmission were taken into account.As the fiber core's radius increases，the electric-field intensity and power dissipation density decrease and the propagation constant increases.Lower ambient temperature，higher convective heat transfer coefficient，and higher surface emissivity can lead to lower propagation constant，higher electric-field intensity，and higher power dissipation density.The changes in power dissipation density and electric-field intensity with the cross-section curvature are not linear and also influenced by other factors.

base-mode transmission；propagation constant；power dissipation density；coupled thermal-optical effects

国家自然科学基金(51176039)资助项目

TK124

A

10.3788/fgxb20153601.0121

1000-7032(2015)01-0121-07

2014-09-28；

2014-11-13

周吉(1986-)，男，湖南湘潭人，博士研究生，2011年于重庆大学获得硕士学位，主要从事光纤电光热多场耦合效应的研究。E-mail：zhouji174@163.com

马宇(1980-)，男，辽宁本溪人，副教授，2008年于哈尔滨工业大学获得博士学位，主要从事光纤电光热多场耦合效应的研究。E-mail：mayu@hit.edu.cn