分数阶Buck变换器的混沌分析与控制

陈 薇,孙会明,孙龙杰

(西安科技大学 电气与控制工程学院,陕西 西安 710054)

分数阶Buck变换器的混沌分析与控制

陈 薇,孙会明,孙龙杰

(西安科技大学 电气与控制工程学院,陕西 西安 710054)

基于电感与电容的分数阶事实,在Matlab/Simulink下建立了电压控制型Buck变换器的分数阶数学仿真模型及对应的电路仿真模型,分析验证了模型的正确性。基于建立的分数阶数学仿真模型,少有文献研究的以参考电压作为混沌控制变量的Buck变换器混沌行为,绘制了以参考电压为混沌变量的Buck变换器V-I混沌相图与对应的分岔图,得出较小的参考电压易引起Buck变换器进入混沌状态。最后,采用参数扰动法实现了混沌控制,得到了新的分岔图,与混沌控制前的分岔图形成了鲜明的对比。同时,通过选定特定的参考电压值,经分析混沌控制前后电感电流的时域波形图,验证了该控制算法的有效性。

分数阶;建模;Buck变换器;混沌控制;分岔;相图

已有的研究表明,实际电容和电感在本质上均是分数阶的[1]。整数阶的电感和电容在实际中并不存在[1-3],以往用于描述电感和电容电特性的整数阶模型是不够准确的,甚至可能是错误的[1]。作为研究和设计开关变换器的关键环节,开关变换器的建模始终是研究的热点问题,尤其是由于开关功率变换器建模是实现开关变换器设计的基础,建模的准确性直接影响到控制器设计性能的高低[1]。采用整数阶模型只能粗略描述,且用整数阶模型描述Buck变换器的动力学行为与变换器的分数阶本质是相违背的[1]。因此,建立变换器的分数阶仿真模型就显得尤为重要。实际上,以往的硬件电路获得的实验结果,本身就是由实际分数阶电感和电容得到的实验结果;而以往基于整数阶电感和电容仿真模型获得的结果与硬件电路获得的结果一致,仅能说明基于整数阶模型建立的仿真是可用来近似分析实际的系统[1-3]。在已有的文献中,对于DC/DC变换器中的混沌现象的研究并不少见,主要有实验电路法和数值仿真法[4-9]。但所有的仿真模型与理论研究方法均是基于电感和电容为整数阶出发建立的仿真模型。在对不同类型的变换器电路的混沌研究中,众多文献均是以电源电压和负载电容[5]、负载电阻[7]、电感[8]、开关频率f[9]为混沌控制变量进行分析和研究的,但Buck变换器电路中的其他参数也可能引发混沌,参考电压Vref就是其中之一。

本文首先基于电容和电感本质上是分数阶的事实结合分数阶微积分理论,在Matlab/Simulink建立了Buck变换器的分数阶数学仿真模型与对应的电路仿真模型,以此模型的仿真结果与已有文献硬件电路和理论分析结果对比验证了模型的正确性。基于此模型,仿真分析了Buck变换器中以参考电压Vref为变量的Buck变换器的混沌行为,获得了对应0.9阶U-I相图;因电路仿真模型充分考虑了开关管和二极管的开关特性,以建立的电路仿真模型绘制对应的分岔图以使结果尽可能的接近实际结果。最后,采用参数扰动控制法[10],即在参考电压Vref上叠加一个与锯齿波信号Vramp同频、同相的正弦谐波信号,将Buck变化器的几种不同的状态控制在了周期稳定状态,达到混沌控制的目的;绘制了控制前后的分岔图、相图、时域波形图,通过这些仿真图验证了控制算法的有效性及模型的正确性。建立Buck变换器的分数阶仿真模型的方法同样适用于建立其他DC/DC变换器的分数阶模型;此分数阶模型的建立有利于促进分数阶微积分理论在DC/DC变换器研究方面的应用,为DC/DC变换器的分析研究提供了新思路。

1 变换器的分数阶建模

由文献[1～3]可知,分数阶电感和电容的数学模型为

(1)

α和β分别为电感和电容的分数阶阶数且0<α,β<1。

根据Grunwald-Letnikov分数阶导数定义分数阶导数的拉普拉斯变换[11-13],即

(2)

图1是电压控制型Buck变换器的电路模型[5-6]。

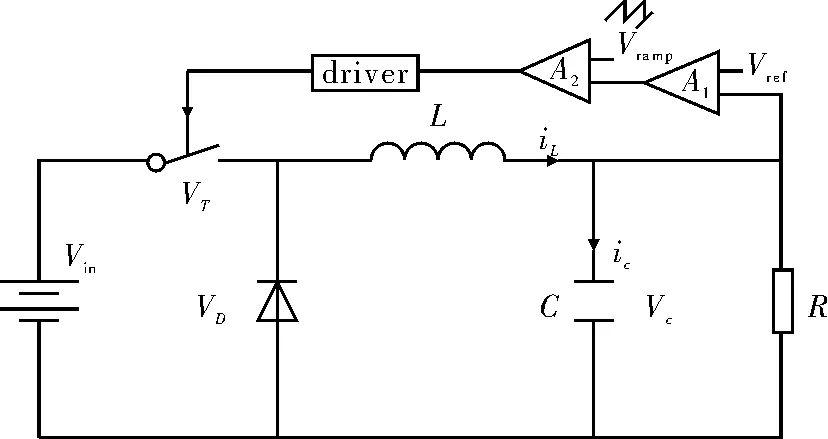
图1 电压控制型Buck变换器电路图

Buck变换器在其开通和关断时等值电路,如图2所示[5]。

(1)当VT导通、VD关断时,图2(a)的状态方程为

(3)

对状态方程进行拉普拉斯变换并整理得

(4)

(2)当VT关断、VD导通时,图2(b)电路的状态方程为

(5)

对状态方程进行拉普拉斯变换并整理得

(6)

以上电路与等式中各个变量的含义如文献[1～3]和[5～6]所述。

2 Matlab/Simulink下的分数阶仿真模型

在文献[5]建立Buck变换器仿真模型的思想启发下,基于Matlab、Simulink软件结合薛定宇等人在Oustaloup滤波器分数阶微积分算法基础上提出的改进算法[11],构建FractionalInts^{-α}的Matlab/Simulink模块,子模块分装内部结构见文献[11]。搭建的分数阶Buck变换器Simulink数学仿真模型如图3所示,对应的电路仿真模型如图4所示。对于图3模型中的3个FractionalInts^{-α}子模块,用积分模块代替之后就获得了整数阶Buck变换器的数学仿真模型。

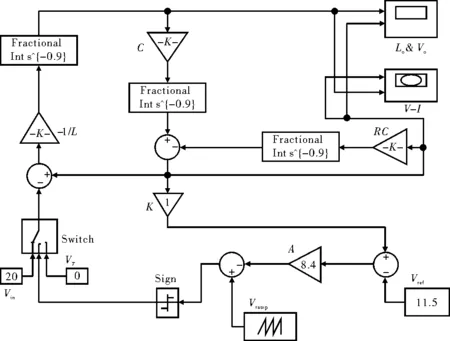
图3 分数阶Simulink数学仿真模型

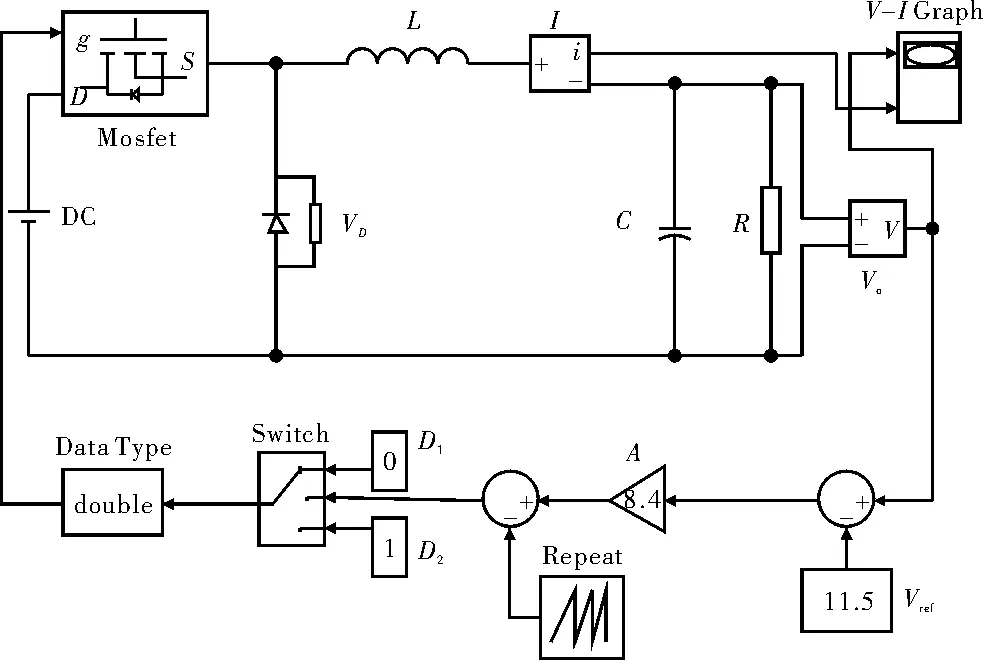
图4 Buck变换器Simulink电路仿真模型

薛定宇等人提出的改进Oustaloup滤波器的分数阶微积分算法有3个关键参数[11]:拟合频率下限ωb、拟合频率上限ωh、滤波器的阶数2N+1。在对实际的分数阶系统进行数值仿真时,需选择合适的拟合频段(ωb,ωh)和N值,一般选择ωbωh=1。对于模块Fractional Int s^{-α}子模块,同样可根据已有文献的结论[12-13],利用分数阶微积分的波特图频域近似算法所得到的1/sq的频域近似式来代替,文献中给出了q从0.1～0.9的近似表达式(最大误差2 dB和3 dB)[12-13]。同样,可利用改进Oustaloup滤波器的分数阶微积分算法得到的传递函数通过降阶[11]后获得低阶次的传递函数来替换Fractional Int s^{-α}模块,而这些方法均可获得相同的仿真结果。因此,模型的使用灵活、简便,并可满足不同的仿真需求。

3 模型的正确性验证

基于建立的分数阶模型,以输入电压Vin、负载电阻R、电感L、电容C、开关周期T为变量仿真获得的相图,与现有文献结果对比验证模型的正确性。文中,仅给出以输入电压Uin、电感L为变量的仿真结果。电路参数为:L=20 mH,R=22 Ω,A=8.4,Vref=11.5,VL=3.8 V,Vh=8.3 V,T=400 μs,K=1[5-6]。当电路中某一参数改变时,其他参数均保持不变。

对于Buck变换器的非线性行为研究,可通过Buck变换器的数学模型,利用计算机数值计算来分析研究,但参考文献[4]提到,由于变换器工作模态的复杂性,基于理想化假设条件下的变换器精确数学模型虽有利于理论分析研究,但精确离散数学模型与实际的电路仍存在较大的误差[9]。在Matlab/Simulink下,由电路仿真模产生分岔图,由于电路仿真模型中采用的是器件级的模型,充分考虑了开关管和二极管的开关特性,使得仿真模型得到的结果尽可能的接近实际的硬件实验结果。此方法简化了分岔图的绘制方法,同时提高了近似精度。为保证分岔图的精确度,又不致使仿真时间过长,对仿真中的几个重要参数进行设置。第1个参数是仿真时间t;第2个参数是相对误差,设置为1e-10;第3个参数是绝对误差,设为1e-13。

在分岔图绘制过程中,每给一个参数值,用程序算出在该参数下对应的状态变量的某一些取值点,将这些取值点画在该参数对应的同一竖线上。若将变量的全部取值点均画在同一竖线上,点数就会过多,从而使图形变得杂乱。故在程序中必须有控制取点数量的程序指令。文中选取相图中的极大值点作为分岔图绘制的绘图点。文中给出了部分0.9阶分数阶和0.8阶分数阶模型在以输入电压Vin、电感L为变量下的分数阶Simulink数学仿真模型的仿真相图;在实际的研究过程中,以输入电压Vin、负载电阻R、电感L、电容C、开关周期T为变量时,均仿真了分数阶0.9和0.8阶以及整数阶Simulink数学模型和Simulink电路模型,获得的相图形状均相同,因此模型对于以这些参数为变量的混沌分析是正确的。同时,对上述若干方法也进行了仿真,观察到了形状相同的相图。

文中所有相图均是由分数阶模型仿真获得的,由于开关周期T=400 μs,则选择ωh>104,ωb<10-4,文中选取ωh=106,ωb=10-6。相图的详细分析见文献[14]。

3.1 电压变化时的仿真结果

图5为输入电压变化时0.9阶分数阶相图,从图中可看出,随着输入电压的增大,电路不再稳定;分数阶仿真模型获得的仿真结果与文献[4～6]结果完全相符。说明此分数阶模型对于Buck变换器以输入电压Vin为变量的混动行为仿真分析是正确的。图6为以输入电压Vin为混沌变量的电感电流分岔图,分岔图反映出的仿真结果与图5所示的U-I相图结果一致。

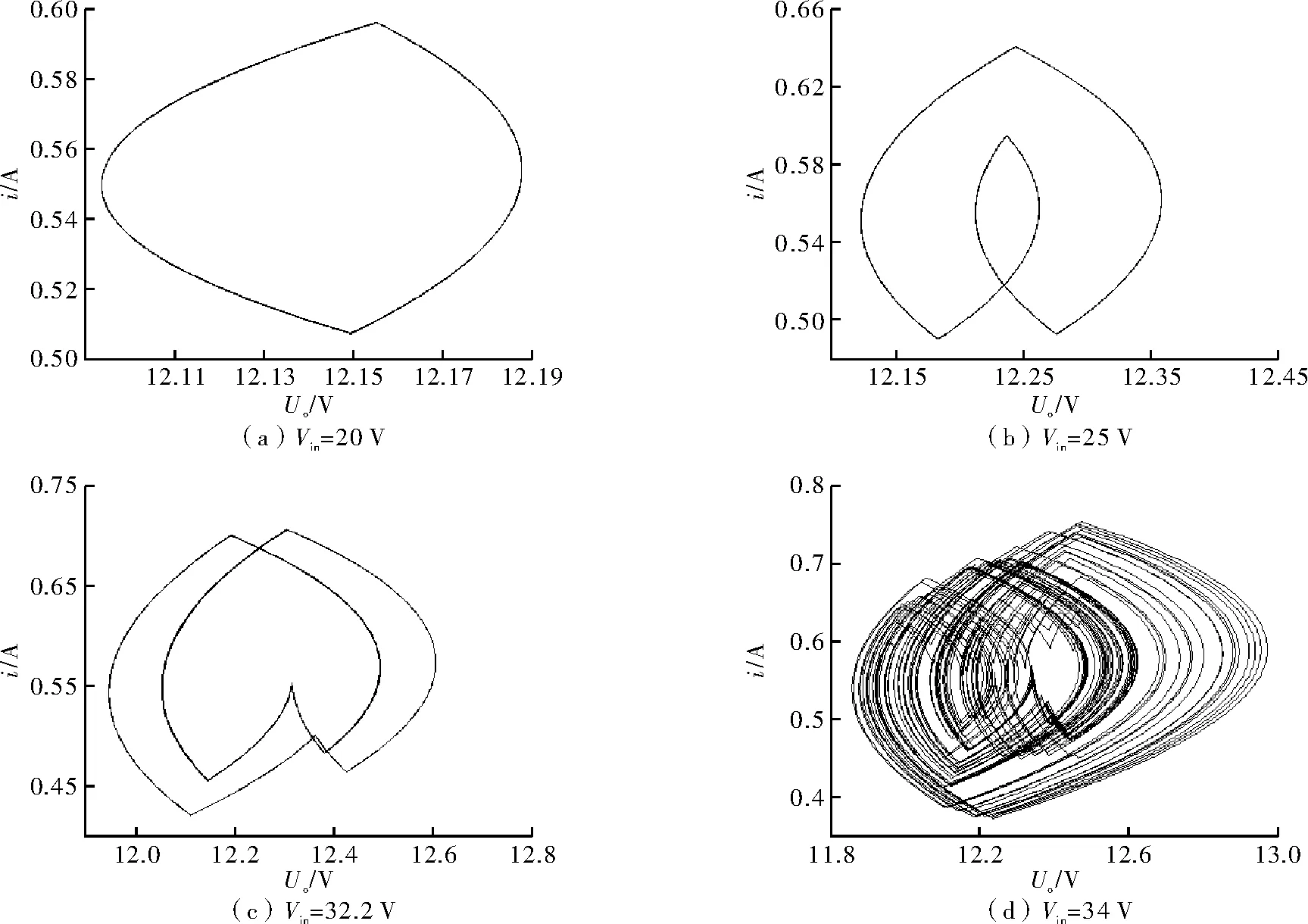
图5 输入电压变化时的相图

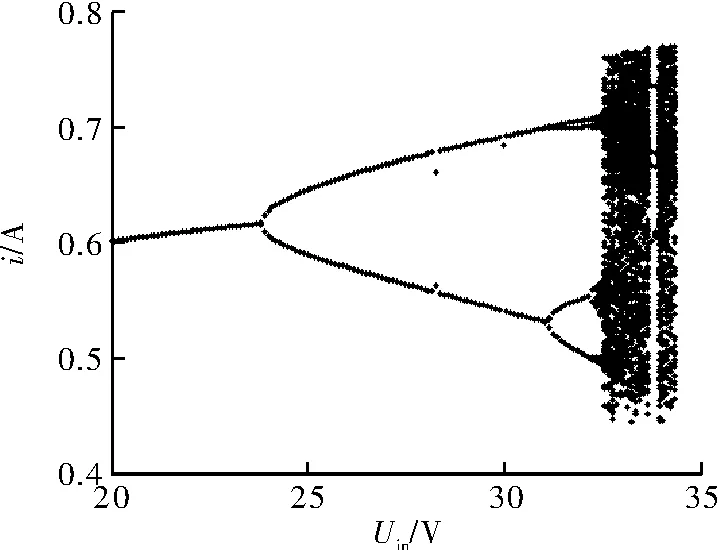
图6 电感电流分岔图

3.2 电感变化时的仿真结果

图7为以电感为变量的电感电流分岔图,分岔图反映出的仿真结果与图8所示U-I相图结果一致。图8是以电感为变量,以0.8阶分数阶模型获得的U-I相图,结果与文献[8]中的仿真结果、分岔图以及硬件电路得到的结论相符。此处给出的相图是Vin=20 V时的结果,而文献[8]中给出的是Vin=34 V时的结果,在实验过程中,Vin=34 V时的仿真结果与文献[8]中完全相同。而给出Vin=20 V时的结果相图与文献[8]形状相同,但相同形状相图对应的电感L值不同,说明了Buck变换器的混沌行为是以上所有参数共同决定的,同时证明了模型的正确性。硬件电路实现见文献[7～9]。

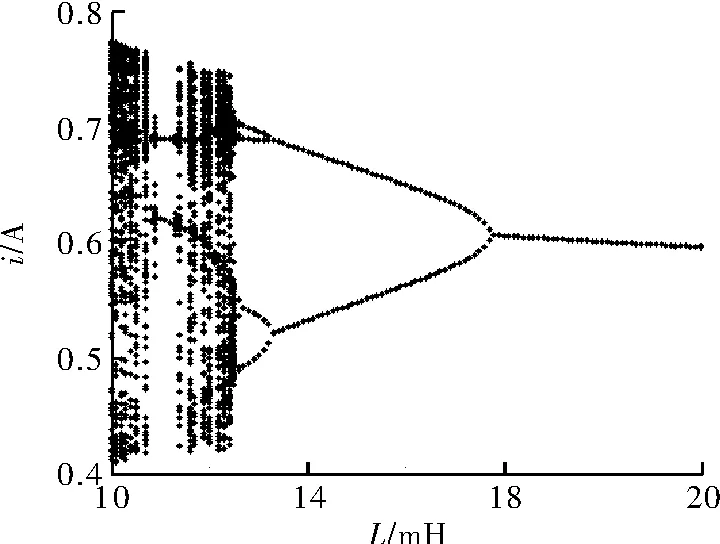
图7 电感电流分岔图

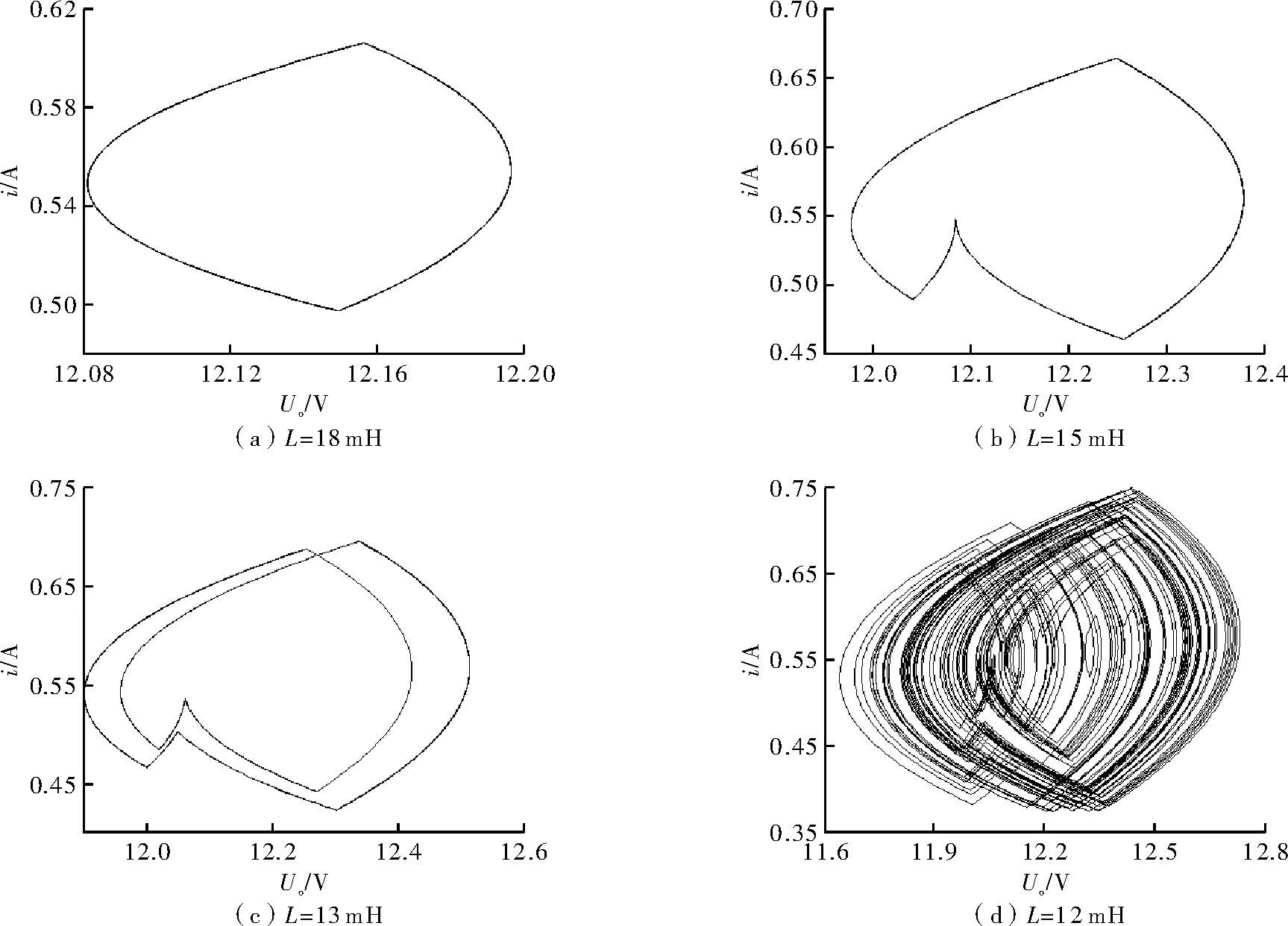
图8 电感L变化时的相图

4 以Vref为变量的混沌仿真

由仿真分析可知,分别以输入电压Vin、输出电容C、负载电阻R、电感L以及开关周期T这5个参数为混沌控制变量仿真了整数阶、0.9阶分数阶、0.8阶分数阶模型,得到的仿真结果与以往的理论分析、仿真和硬件电路获得的结果相同,所建立的分数阶模型可准确地仿真Buck变换器的混沌行为。分数阶模型得到的仿真结果与以往硬件电路获得的结果是一致的,至少说明了在此建立的分数阶模型能与以往基于电容和电感为整数阶建立的理论分析和模型获得的结果等同。

对以Vref为变量的混沌仿真采用分数阶模型进行仿真,此处仅给出分数阶模型获得的部分仿真相图。电路参数为Vin=20 V,C=47 μF,L=20 mH,R=22 Ω,A=8.4。以Vref为变量、电路仿真模型绘制的分岔图如图9所示。

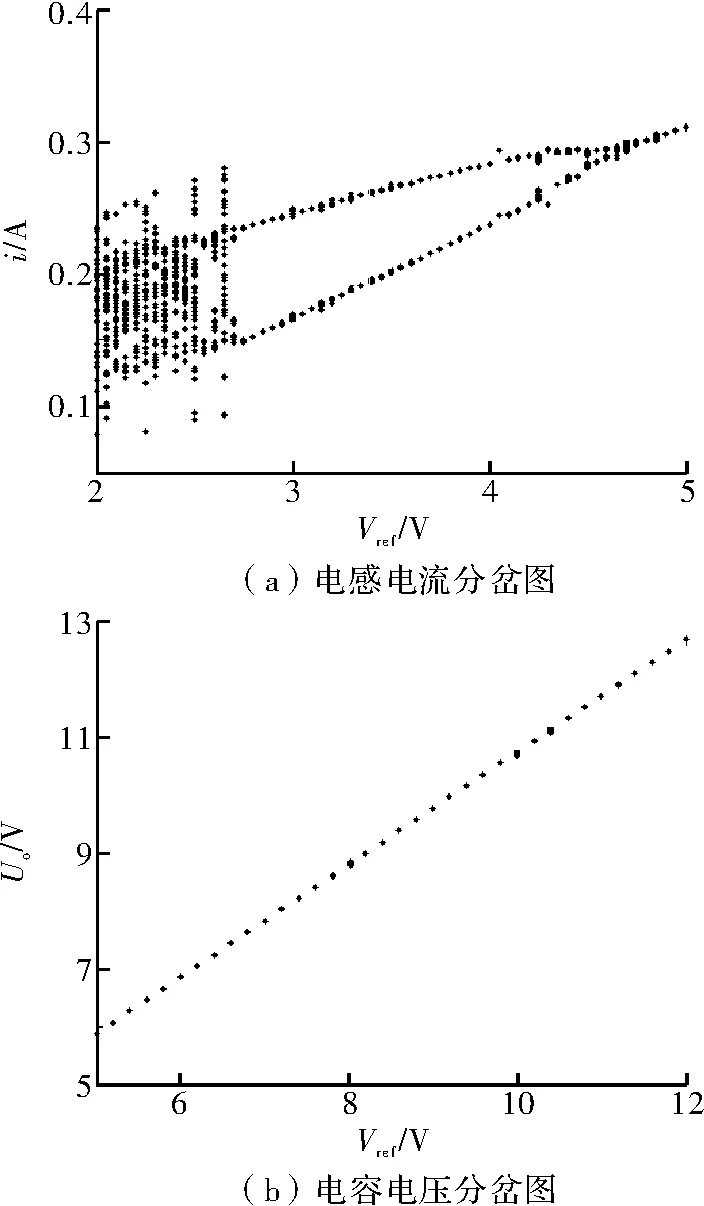
图9 未加控制前分岔图

图9(a)为Vref∈[2,5]时的电感电流分岔图,Vref∈[5,12]的分岔图为一直线,电感电流分岔图与电容电压分岔图形状相似,分岔点位置一致,因此未给出,但给出了Vref∈[5,12]时的电压分岔图。由分岔图可看出,Vref∈[2,2.4]时,状态变量处于混沌状态;Vref∈[2.5,2.7]时,状态变量处于多倍周期状态;Vref∈[2.8,4.7]时,状态变量处于2倍周期分岔;Vref∈[4.8,12]时,状态变量处于单周期稳定状态,即较小的参考电压可能导致Buck系统工作在混沌状态。

图10为0.9阶分数阶数学仿真模型获得的相图。Vref=10 V时,工作在稳定的周期1状态;当Vref=4 V时,工作在2倍周期分岔;Vref=2.7 V,相图为周期5相图;Vref=2 V,为混沌相图;相图获得结果与分岔图反映的结果相符。

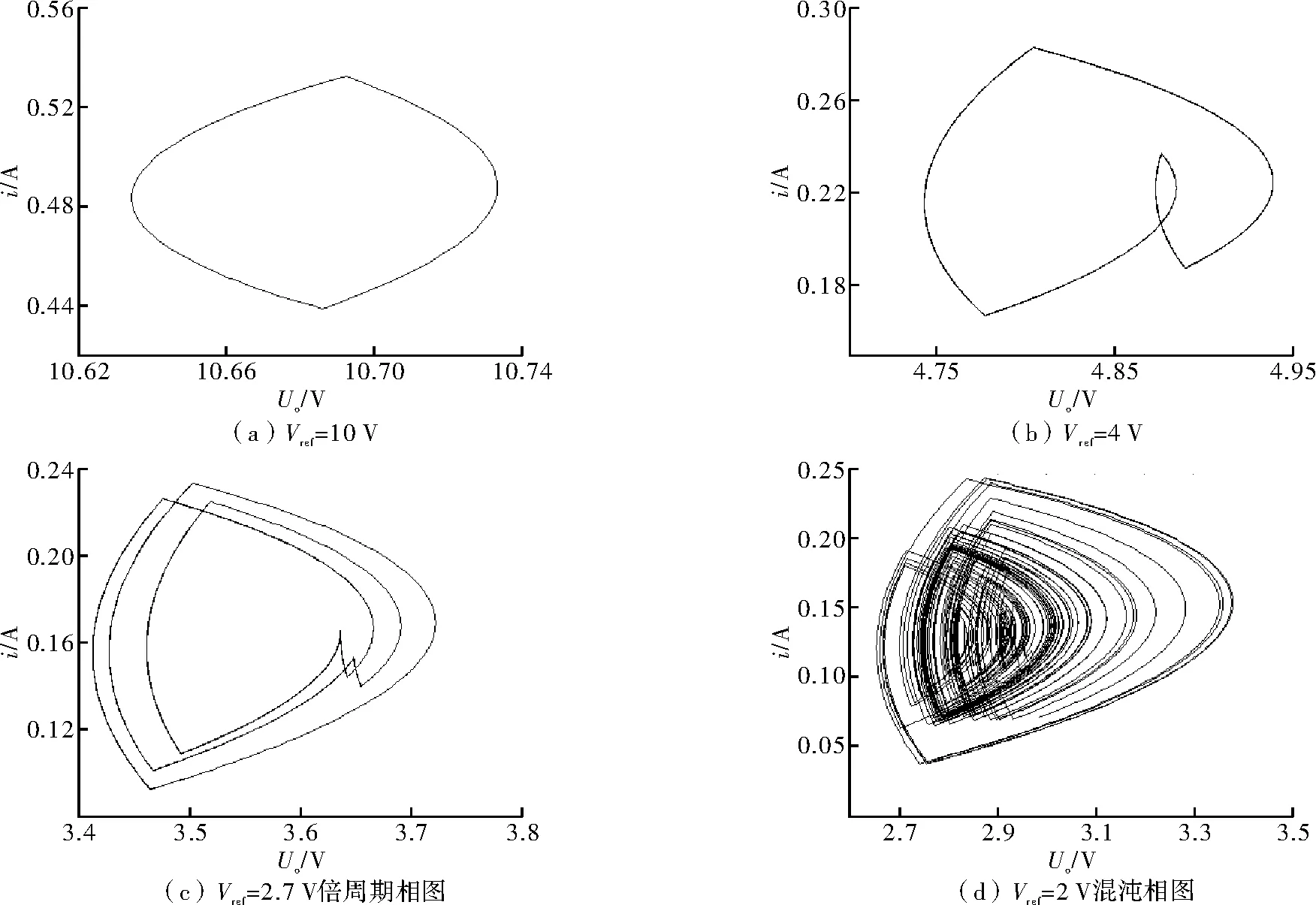
图10 参考电压Vref变化时的相图

5 混沌控制

系统处于分岔、混沌状态时,电感电流、电容电压的波形含有较多的高次谐波,长时间后会带来负面的影响,混沌控制就是要控制其不出现混沌现象,控制其状态变量在稳定单周期状态。参数扰动控制法是一种简单的非反馈混沌控制方法,其适合非自制系统的混沌控制,而Buck变化器是典型的非自制系统;因此,在锯齿波信号Vramp或参考电压Vref上叠加一个随机信号或混沌信号来实现。为实现简单,文中采用在参考电压上叠加一个与Vramp信号同频、同相位的正弦信号,通过大量仿真分析,正弦信号赋值K选择为2 V。即

Vref→Vref+Ksin(2πft)

(7)

图11为Buck变换器对应的几种工作状态在加入混沌控制算法后的分岔图,与未加控制前的分岔图对比可发现其发生了明显变化,原分岔图如图9所示,原来的4种不同状态均被控制在了稳定的周期一状态。以分数阶模型为基础,选择Vref=2V时的电感电流时域波形如图12所示。从图中可看出,未加控制前,波形处于一种无周期的混沌状态,加入控制后,波形经历了短暂的过渡期后趋于单周期稳定。图13为Vref=2V时分数阶模型在加入控制算法后获得的U-I相图,与图10(d)对比,可看到控制效果明显。

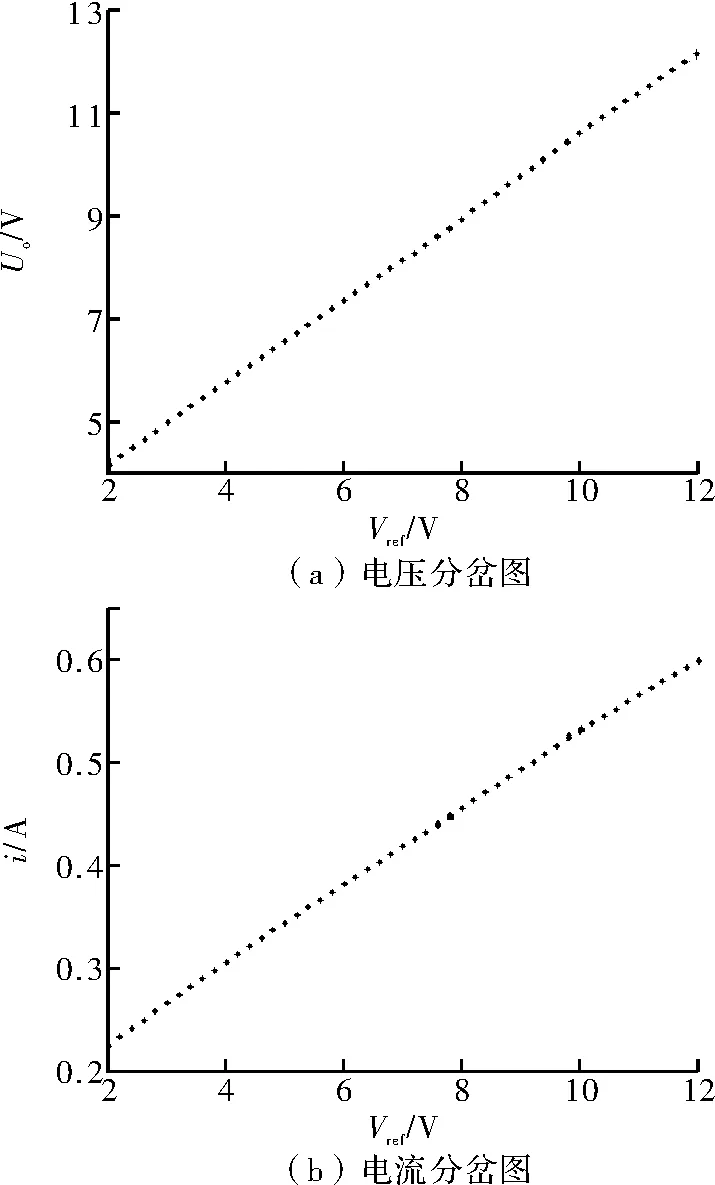
图11 加入控制算法后的分岔图

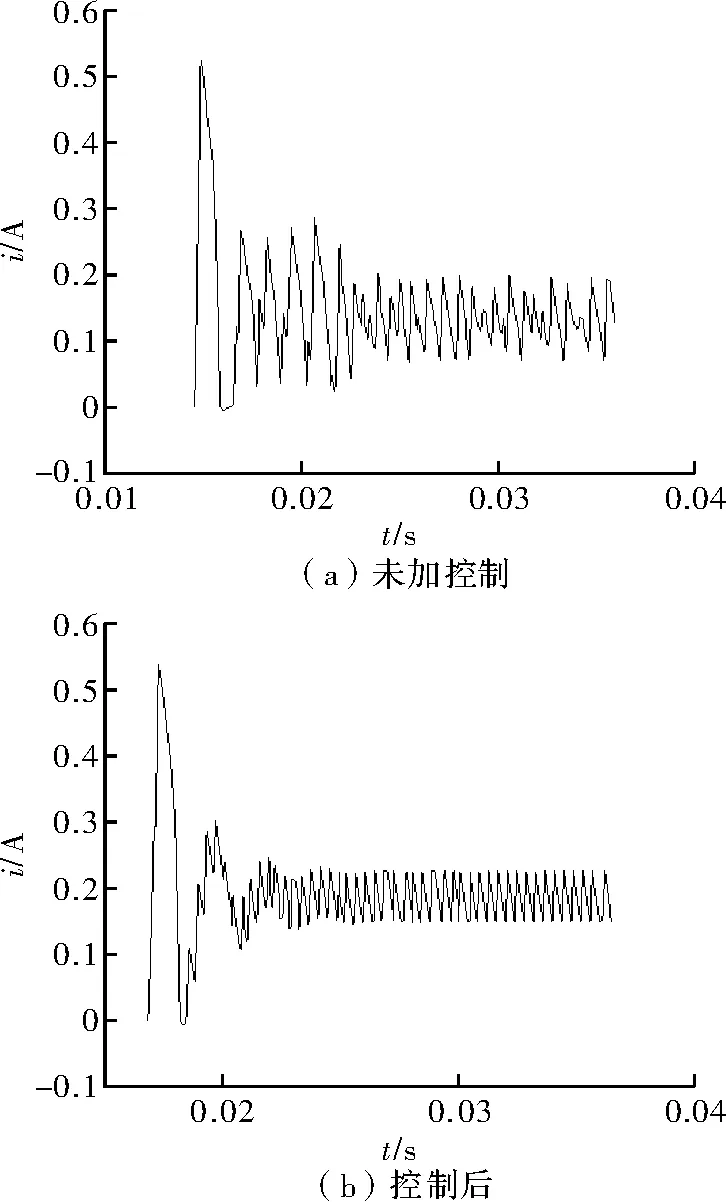
图12 Vref=2 V时的时域波形图

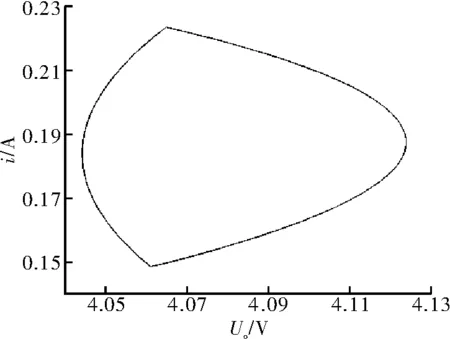
图13 Vref=2 V时加入控制算法后的相图

6 结束语

本文在Matlab/Simulink仿真软件下建立了Buck变换器的分数阶数学仿真模型及Simulink电路仿真模型,分析验证了模型的正确性;通过此模型研究了现有文献较少涉及到的以参考电压Vref为变量的电压控制型Buck变换器的混沌及其控制技术;采用Simulink电路模型编程获得了分岔图;给出了部分分数阶模型的仿真相图。基于此模型仿真分析了大多文献研究过的其他几个参数为变量的混沌行为,均获得了相同结果,通过仿真分析发现:

(1)较大的输入电压Vin、较大的负载电阻R、较大的开关周期T、较小的负载电容C、较小的电感L、较小的参考电压Vref均可能导致系统出现混沌状态;正确选择电路参数对Buck变换器的稳定运行具有重要意义。对变换器的设计、优化、故障分析提供了有用的参考。

(2)加入混沌控制算法后,得到了分岔图、时域图和相图,与控制之前的结果形成了对比,证明了控制算法的有效性。

(3)由于电感和电容本身是分数阶的,则对于分数阶模型和整数阶模型这两种模型均可正确分析系统动力学行为这一事实,需进一步分析具体某一模型能更精确地反映实际系统的动力学行为及模型的局限性等。同时,建立此模型的方法也可用于建立其他DC/DC变换器的分数阶模型。

[1] 谭程,梁志珊.电感电流伪连续模式下Boost变换器的分数阶建模与分析[J].物理学报,2014,64(7):58-67.

[2] 王发强,马西奎.电感电流连续模式下Boost变换器的分数阶建模与仿真分析[J].物理学报,2011,60(7):96-103.

[3] 王发强,马西奎.基于分数阶微积分的电感电流断续模式下Boost变换器的建模与分析[J].中国科学:技术科学,2013,43(4):368-374.

[4] 张波,曲颖.BUCK DC/DC变换器分岔和混沌的精确离散模型及实验研究[J].中国电机工程学报,2003,23(12):99-103.

[5] 王春芳,王开艳,李强.Buck变换器仿真模型及分岔与混沌研究[J].系统仿真学报,2007,19(24):5824-5831.

[6] 王开艳,王春芳,张玲丽.CCM和DCM模式Buck变换器建模与混沌现象仿真[J].系统仿真学报,2008,20(14):3881-3887.

[7] 金爱娟,陈建霖,夏震,等.PWM Buck变换器阻性负载引起的混沌及其控制[J].系统仿真学报,2014,26(2):394-397.

[8] 李磊,金爱娟,夏震,等.PWM Buck变换器电感引起的混沌及其控制[J].微特电机,2013,41(10):58-60.

[9] 金爱娟,邢军,赵东方,等.Buck变换器频率引起的混沌及其控制[J].控制工程,2014,21(1):66-69.

[10]Basak B,Parui S.Exploration of bifurcation and chaos in buck converter supplied form a rectifier[J].IEEE Transaction on Power Electronics,2010,25(6):1556-1564.

[11]薛定宇,陈阳泉.控制数学问题的Matlab求解[M].北京:清华大学出版社,2007.

[12]刘崇新.分数阶混沌电路理论及应用[M].西安:西安交通大学出版社,2011.

[13]高心,刘兴文,邵仕泉.分数阶动力系统的混沌、控制与同步[M].成都:电子科技大学出版社,2010.

[14]包伯成.混动电路导论[M].北京:科学出版社,2013.

[15]Oustaloup A,Levron F,Mathieu B,et al.Frequency-band complex noninteger differentiator:characterization and synthesis[J].IEEE Transactions on Circuits Systems I:Fundam Theory Application,2000,47(1):25-39.

[16]张卫平.开关变换器的建模与控制[M].北京:中国电力出版社,2005.

[17]Xie F,Yang R,Zhang B.Bifurcation and border collision analysis of voltage-mode-controlled flyback converter based on total ampere-turns[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2011,58(9):2269-2280.

[18]罗晓曙,汪秉宏,陈关荣,等.DC-DC变换器的分岔行为及混沌控制研究[J].物理学报,2003,52(1):12-18.

Chaotic Analysis and Control of Fractional Order Buck Converter

CHEN Wei,SUN Huiming,SUN Longjie

(School of Electrical and Control Engineering,Xi’an University of Science and Technology,Xi’an 710054,China)

Based on the Fractional facts of inductance and capacitance in Matlab/Simulink,this paper establishes a mathematical simulation model of the fractional order Buck converter and the corresponding circuit simulation model.The correctness of the model is verified.Based on the fractional order of the mathematic simulation model,we study the literature researches,which are rare,on the reference voltage as the control variables of the chaos.We also draw the phase diagram and the corresponding bifurcation diagram of the Buck converter variableV-Ichaos with the reference voltage as the chaos variable.It is shown that a smaller reference voltage is more likely to cause the chaotic state of the Buck converter.Finally the parameter interference method is used to control the chaos.And a new bifurcation diagram is obtained,which constitutes a sharp contrast with the one before the chaos is controlled.By selecting a given reference voltage value and analyzing the time domain waveform diagrams of the induced current before and after the chaos is controlled,the control algorithm is shown to be effective.

fractional;modeling;Buck converters;chaos control;bifurcation;phase diagram

2014- 11- 12

陕西省教育厅科学研究基金资助项目(14JK2055;14JK2056)

陈薇(1987—),女,硕士,助理工程师。研究方向:智能仪器仪表工程。E-mail:1246182611@qq.com。孙会明(1988—),男,硕士研究生。研究方向:智能算法,信号处理,混沌控制与同步。孙龙杰(1965—),男,博士,副教授,硕士生导师。研究方向:嵌入式系统开发,集成电路等。

10.16180/j.cnki.issn1007-7820.2015.05.026

TP39;TP11

A

1007-7820(2015)05-087-07