MIMO雷达信号的盲源分离技术
方 健
(西安电子科技大学 电子工程学院,陕西 西安 710071)
MIMO雷达信号的盲源分离技术
方 健
(西安电子科技大学 电子工程学院,陕西 西安 710071)
针对MIMO雷达的信号特点,采用了一种多角度的雷达侦察方法,从不同的方位获取同一部雷达的独立信号样本。并在此基础上,运用主分量分析方法估计信号波形个数,运用独立分量分析的盲源分离方法分离出MIMO雷达信号的各个正交分量,最终以正交频分线性调频信号为例,在信噪比为0dB的情况下对该信号进行了仿真分析,其结果验证了该方法的有效性。
MIMO雷达;侦察识别;盲源分离;主分量分析;独立分量分析
MIMO(Multiple-Input Multiple-Output)雷达自第37届Asilomar信号、系统与计算机会议上被提出以来[1],就受到了广泛关注,其在低截获概率和抗干扰等方面有着突出的性能,与相控阵雷达的相比其所体现出的优越性展示了巨大的发展潜力[2]。
另一方面,针对MIMO这种体制的雷达对抗技术也在不断研究,由于MIMO雷达是同时发射多个正交波形,在空间上信号是线性混叠的,在频谱上仍可能存在部分重叠现象,因此研究的难点在于准确估计信源个数以及如何对MIMO雷达的线性混叠信号进行有效分离。盲信号处理技术[3]作为上世纪80年代末提出的一种全新的信号处理技术,具有坚实的理论基础和许多潜在的应用,已成为现代信号处理领域一个较为活跃的方向。由于无先验信息,MIMO雷达信号对于侦察机而言本身就是盲信号,因此采取盲信号处理技术是MIMO雷达侦察的一个重要途径。本文采用了一种满足盲源分离算法条件的侦察模型,主要研究了主分量分析(Principal Component Analysis,PCA)结合独立分量分析(Independent Component Analysis,ICA)的盲源分离(Blind Source Separation,BSS)方法对常见的MIMO雷达信号的分离的效果。
1 MIMO雷达的基本原理
MIMO雷达采用正交信号的相控阵雷达,其发射天线阵列分为M个阵元,每个阵元发射的信号相互正交,这些多波形信号经由目标散射被N个阵元接收,由于存在正交关系,各信号在空间中能保持相互独立性,在发射阵元和接收阵元的空间中便存在MN个通道[1]。
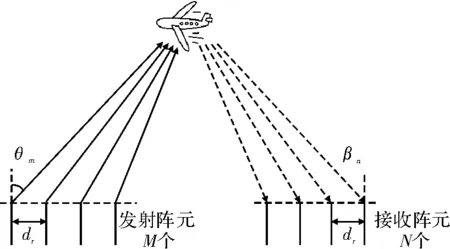
图1 MIMO雷达的工作模型
接收端每个阵元将可接收到M个信号的混合信号,使用M个匹配滤波器分别对接收到的回波信号进行匹配滤波,这样通过正交性分选,每个接收阵元可得到M路信号输出,然后对这MN路信号移相求和,实现接收数字波束形成[4],最后通过一定的算法对每个波束输出信号进行目标检测和参数估计,例如文献[5]对MUSIC、Capon和GLRT到达角估计算法进行了仿真研究。
2 侦察模型
为满足盲源分离算法的约束性条件[6],即:(1)各源信号统计独立。(2)混合矩阵列满秩且观测信号维数不少于源信号维数。(3)源信号中至多有一个高斯信号,且为平稳随机过程。MIMO雷达发射的是正交波形,一般采用正交频分线性调频信号、相位和离散频率编码信号等,而侦察机截获的信号为多个正交波形的混合,这使得条件(1)和(3)已满足。为了也能满足条件(2),使侦察机在不同的方位对MIMO雷达进行侦察,假设MIMO雷达有M个正交发射波形,则根据盲源分离的约束条件,侦察次数K应满足K≥M。如图2所示,K次侦察的位置相对于雷达阵面法线方向的角度构成向量[θ1,θ2,…,θK]。
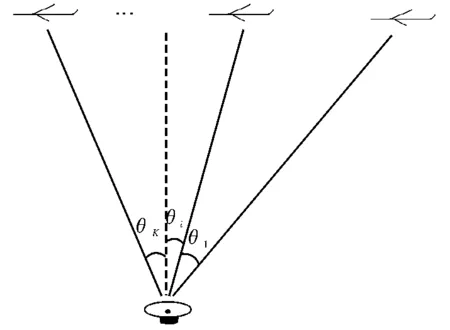
图2 MIMO雷达侦察模型
模型中,假设MIMO雷达发射阵列为紧凑阵,阵元间距较小。每次侦察到的信号样本是M个正交波形的线性混合信号,即
Yi=gt(θi)TS(t-τi)+Ni(t),i≤K
(1)
式中,gt(θi)=[1,e-jφi,e-j2φi,…,e-j(M-1)φi]T为发射导向矢量,φi=2πdsinθi/λ为发射通道空间相位差,θi为侦察机某一次侦察相对于雷达阵面法线方向的角度,S(t)=[s1(t),s2(t),…,sM(t)]T表示MIMO雷达发射的M个正交波形矢量,τi=Ri/c为雷达信号的传播迟延,Ni(t)为随机噪声向量。从式(1)可看出,侦察到的MIMO雷达信号模型为盲源分离中的瞬时线性混合模型,显然运用上述的侦察方法获得的信号样本空间已经满足了盲源分离算法的条件。
3 算法分析
盲源分离算法有很多种,比较常见的如独立分量分析(ICA)、最大似然估计(Maximum Likelihood,ML)等[7],本文采用快速独立分量分析(FAST-ICA)算法,这是一种复杂度和性能都较优越的算法[8]。
对于信源数目的估计是盲源分析首先要解决的问题,本文采用主分量分析方法(PCA),其是一种降维的统计方法,通过“主成分”变量分析,只保留对信息整体贡献较大的成分,从而达到压缩数据空间的目的。PCA的本质是对角化协方差矩阵,借助于奇异值分解或特征值分解可得到“主成分”变量[9]。采用PCA算法一方面可以估计MIMO雷达分集波形的数量,另一方面减小了输入数据的冗余,从而降低了后续算法的运算时间。
独立分量分析(ICA)用来分离统计独立的源信号,是盲源分离算法的一种特殊情形,因盲源分离算法本身并不要求分离后的信号是统计独立的,但鉴于MIMO雷达信号的特殊性,即发射的各源信号是相互正交、统计独立的,因此ICA算法在MIMO雷达的盲源分离检测方面非常适用。
无论使用PCA还是ICA算法都需要对信号预处理,预处理步骤包括去均值和白化。对于观测到的雷达信号Y,E(Y)表示其均值,则去均值后信号
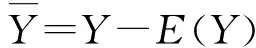
(2)
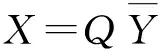
(3)
则白化后观测信号可表示为
(4)
上式中D为对角矩阵,包含特征值
(5)
将特征值从大到小排序,如λ1>λ2>…>λN-1>λN,则选取前面几个较大的特征值,选取准则可通过贡献率来衡量,每个特征值的贡献率为
(6)
从1~N计算累计贡献率,当累计贡献率超过设置的门限时停止计算,此时参与计算的特征值个数为主分量数量估计值,即信源的个数的估计值;相应地,保留的特征值对应的特征向量组成新的特征向量组M,本文仿真取累计贡献率门限为0.99。
FAST-ICA[10]是ICA算法的快速版本,它的核心思想是通过最大化各分量的非高斯性来完成盲源分离,算法本身来源于自适应处理,并在计算中运用了批处理的方法,因此拥有较快的处理速度。
ICA=目标函数+优化方法,为了抽取各个独立分量,目标函数的选取准则是要使分离后数据的概率密度函数距离高斯分布最远,因此采用负熵的概念来度量非高斯性最为合适,负熵定义为
J[x]=H(xgauss)-H(x)
(7)
其中,H(·)表示信息熵;xgauss是与x具有相同协方差矩阵的高斯随机向量。在实际中,通常采用4阶累积量作为计算负熵的近似方法相对简单。对于FAST-ICA算法,目标函数定义为
J(x)≈(E{G(x)}-E{G(v)})2
(8)
其中,G为非二次函数,并采用牛顿迭代算法对目标函数进行近似和优化,得到定点迭代公式
(9)
(9)
其中,W为分离向量;WTx为分离后的信号,收敛条件为
(10)
其中,ε为收敛系数,本文取ε=0.000 1。综上所述,针对MIMO雷达信号进行盲源分离的步骤可归纳为:(1)对信号预处理(去均值和白化),使用PCA算法估计信源个数、降低数据冗余。(2)选定一个非二次函数g(x),如g(x)=x3。(3)选择初始化随机矩阵W,按式(9)对W进行迭代调整,直到满足收敛条件或达到最大迭代次数为止。(4)计算WTx得到分离信号。(5)对分离信号进行相关检测,判断是否为正交信号。
4 仿真
正交频分线性调频(OFDM-LFM)信号是MIMO雷达的常用波形之一,本文以这种波形为例,进行了盲源分离的仿真实验。假设MIMO雷达有4个发射阵元,每个阵元发射的线性调频信号的带宽为4.0 MHz,脉冲宽度为80 μs,第一阵元的起始频率为10.0 MHz,相邻阵元的频率相差一个带宽,即4.0 MHz。由于每个阵元信号占用不同的频带,因此这种波形满足相互正交性,图3显示了4个原始波形的归一化互相关函数。

图3 原始波形(OFDM-LFM)的互相关函数
为考察在不同信噪比情况下,PCA估计信源数量的性能,在信噪比为-10~10dB范围内,对源信号的混合矩阵A设为随机矩阵,PCA样本空间为6组混合信号,进行了100次蒙特卡罗实验。从图4可看出,在信噪比SNR>0 dB时,正确率已超过85%。

图4 信噪比对信源数量估计的影响
假设侦察机分别在与雷达阵面法线方向夹角45°、40°、30°、15°、20°和25°这6个方位分别侦察到该雷达发射的信号,通过加入高斯白噪声,使得样本信号的SNR降低到0 dB,再运用盲源分离算法对这6组样本信号进行处理,一般能正确地估计出信源数量为4个。图5显示了分离后4个信号的频谱,可看出与设计波形的频谱基本一致,只是顺序发生了错位,这是盲源分离算法不可避免的缺陷之一,但实际上在此也并不关心信号的顺序。
为了评估分离效果,引入相似系数作为评估标准
(11)
0<ρij<1,ρij越接近于1,则表明两个信号越相似,接近于0则表明信号相似性最差。表1为本次分离结果的相似系数矩阵,表中数值较大的表示相似度较高,由于分离后的顺序可能与原信号顺序不一致,因此表中最值出现的位置不一定在对角线上。
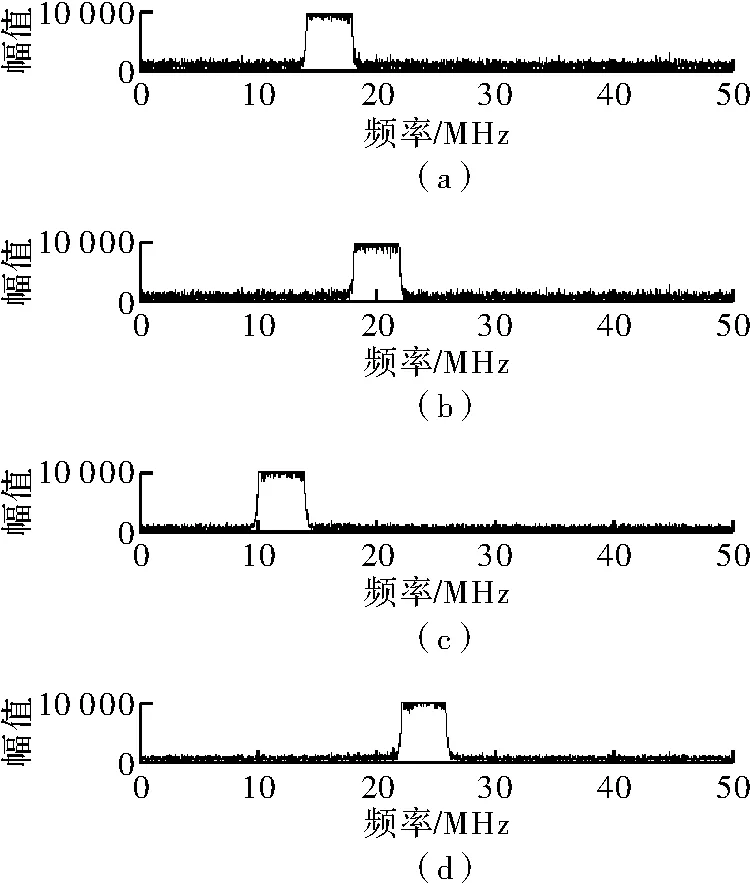
图5 分离信号(OFDM-LFM)的频谱
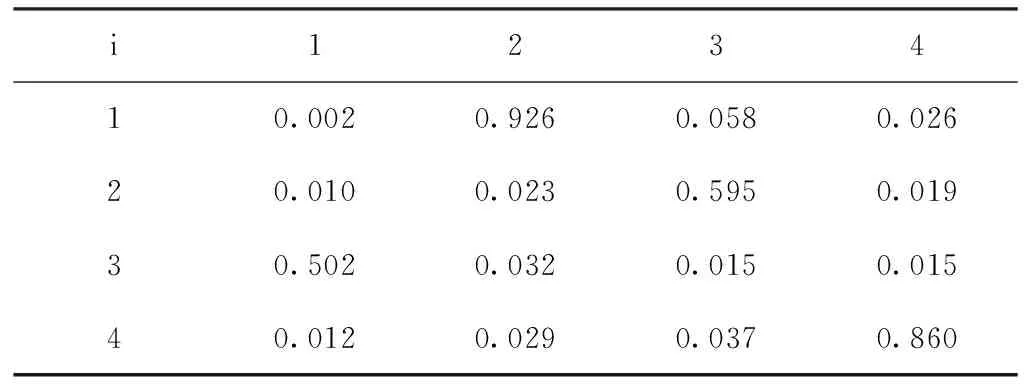
表1 相似系数矩阵
图6显示了分离的4路信号的归一化互相关函数,由图可看出互相关性较差,其与原始波形的互相关函数相似,从而验证了该雷达是MIMO体制雷达。此外,对于盲源分离后得到的信号做进一步处理,还能估计更多该雷达的具体参数。
图6 分离信号(OFDM-LFM)的互相关函数5 结束语
本文针对MIMO体制雷达的信号特点,采用了一种满足盲源分离算法的侦察模型,通过PCA+ICA的盲源分离算法对该模型进行了仿真,其结果显示即使SNR为0 dB,依然能较为准备地估计出信源个数及有效地分离出各个正交信号分量。另外,文中还对正交多相编码信号以及正交离散频率编码做了相似的仿真,结果显示同样有效适用。但本文所涉及到MIMO雷达信号的分选和处理方法还仅为一个轮廓或方向,尚未考虑更多细节,因此仍需进一步深入研究。
[1] 王怀军,许红波,陆珉,等.MIMO雷达技术及其应用分析[J].电光与控,2013,20(12):46-50.
[2] 梁百川.对MIMO雷达的电子侦察技术[J].舰船电子对抗,2008,31(5):17-19.
[3] 张贤达,保铮.盲信号处理[J].电子学报,2001,29(12):1766-1771.
[4] 成芳.正交波形MIMO雷达中信号处理与仿真实验研究[D].成都:电子科技大学,2008.
[5] 董自通.双基地MIMO雷达的干扰研究[D].西安:西安电子科技大学,2013.
[6] Comon P.Independent component analysisa new concept[J].Signal Processing,1994,36(3):287-314.
[7] 高建彬.盲源分离算法及相关理论研究[D].成都:电子科技大学,2012.
[8] 李睿.通信信号的盲源分离算法研究[D].苏州:苏州大学,2011.
[9] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.
[10]Bell R S.Fast and robust fixed-point algorithms for independent component analysis[J].IEEE Transactions on Neural Networks,1999,10(3):626-634.
Blind Source Separation Method for MIMO Radar Signal
FANGJian
(School of Electronic Engineering,Xidian University,Xi’an 710071,China)
In view of the characteristics of the MIMO radar signal,a multi-angle radar reconnaissance method is adopted in this article.By collecting independent signal samples of the same radar in different directions,Principal Component Analysis(PCA) can be used to estimate the number of signal waveform and Independent Component Analysis(ICA) can be used to isolate all quadrature components of the MIMO radar signal.Finally,in the case of SNR being 0dB,the orthogonal frequency division multiplexing-linear frequency modulation signal is taken as an example for simulation and analysis.Results show that this method is effective.
MIMO radar;reconnaissance identification;blind source separation;PCA;ICA
2014- 10- 07
方健(1988—),男,硕士研究生。研究方向:电子信息对抗。E-mail:xiaofang99@139.com
10.16180/j.cnki.issn1007-7820.2015.05.023
TN
A
——以鲁甸地震相关新浪微博为例

