一种稳健的两维两脉冲杂波相消方法
薛海伟,冯大政,周 延
(西安电子科技大学 雷达信号处理国防科技重点实验室,陕西 西安 710071)
一种稳健的两维两脉冲杂波相消方法
薛海伟,冯大政,周 延
(西安电子科技大学 雷达信号处理国防科技重点实验室,陕西 西安 710071)
两维两脉冲杂波对消方法,可以有效地杂波迹进行杂波预滤波,进一步提高后续空时自适应算法的动目标检测性能。但在实际中不准确的载机速度和偏航角等雷达系统参数信息,会制约其杂波抑制性能。为了解决这一问题,文中提出了一种稳健的两维两脉冲杂波相消方法,该方法进一步将载机速度和偏航角误差作为先验知识加入到滤波器系数矩阵设计中,提高了TDPC在雷达系统参数存在误差时的稳健性。并分别利用仿真数据和MCARM实测数据进行了验证。实验结果表明,在载机速度和偏航角存在误差的情况下,相比较TDPC,RTDPC能更加有效地对消杂波,改善了后续空时自适应算法的动目标检测性能。
空时自适应处理;预滤波;杂波抑制
机载相控阵预警雷达需要从强背景杂波中检测和识别目标,其首要问题就是抑制杂波[1-2]。与地基雷达不同,机载雷达由于载机平台的运动而导致杂波呈现出很强的空时耦合性,即不同距离上的杂波回波具有不同的多普勒频率。空时自适应处理(Space-Time Adaptive Processing,STAP)能在时域和空域上联合自适应抑制杂波,提高杂波抑制能力和动目标检测性能,但全维STAP估计杂波协方差矩阵所需的独立同分布训练样本数量巨大,实际无法满足[3-4]。因子法(Factored Approach,FA)、扩展因子法(Extended Factored Approach,EFA)等传统降维STAP[5-9]方法能大幅降低训练样本需求量,在理想情况下能获得与全维STAP几乎相同的性能。但实际中误差会显著恶化降维STAP的性能。合理的利用先验知识可以有效地改善动目标检测性能,利用雷达工作参数和载机平台速度等参数的两维两脉冲杂波对消器(Two-Dimension Pulse-To-Pulse Canceller,TDPC)能有效抑制杂波[10]。但是TDPC抑制杂波的有效性依赖于先验知识的准确程度。雷达参数如波长、脉冲重复频率(Pulse Repetition Frequency,PRF)、阵元间距等在系统工作时可以准确获得,但是实际中复杂的飞行环境会影响载机速度和偏航角的准确估计,这会制约TDPC在实际工作中的应用。
针对这一问题,本文提出了一种稳健的两维两脉冲相消(Robust Two-Dimensional Pulse-To-Pulse Canceller,RTDPC)杂波抑制方法,它将载机速度和偏航角误差也作为先验知识加入到滤波器系数中,这样即使是不准确的载机速度和偏航角也不会影响TDPC抑制杂波的能力,进一步提高了TDPC在实际工作中的稳健性。同样用该方法作为传统空时自适应处理算法的预滤波器,后续空时自适应处理算法的性能也会得到改善。
1 信号模型
假设雷达天线为均匀线阵结构,或者是面阵经微波合成的等效线阵结构,阵元数为N,一个相干处理间隔(Coherent Processing Interval,CPI)内的脉冲数为K。脉冲重复频率为fr。载机以与阵列方向夹角为θp的速度v飞行。将第l个距离单元沿方位角均匀分为Nc个杂波散射单元,并且第l个距离单元上的第i个杂波散射单元对应的方位角和俯仰角分别记为θi和φi,记cn,k(l)为第l个距离环上第n个接收阵元接收的第k个发射脉冲返回的杂波数据[2]

ωs(θi,φl)+(k-1)ωt(θi,φl)]}
(1)
其中,ρi为反射单元的杂波反射系数;F(θi,φi),G(θi)分别为发射和接收方向图;Rl为斜距,而
(2)
(3)
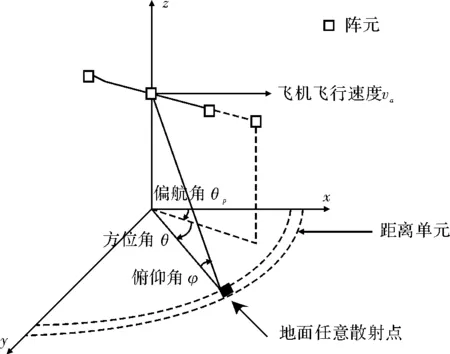
图1 机载相控阵雷达系统
设N根天线第k次接收回波为
c(k)=[c1,k,…,cN,k]=SF(k)ak
(4)
其中
(5)
上式中符号diag(·)表示对角化向量,矩阵F(k)和S分别包含了一个距离环内所有方向杂波回波的多普勒和空域相位,而向量ak则包含了一个距离环内所有方向杂波回波的幅度。
2 稳健两维两脉冲杂波相消器原理
设杂波回波在一个CPI内的起伏缓慢,即ak=ak+1[10]。N根天线第k+1次接收回波为
c(k+1)=[c1,k+1,…,cN,k+1]=SF(k+1)ak
(6)
比较F(k)和F(k+1)可知
F(k+1)=F(k)diag([ω1(φl,θ1),…,ω1(φl,θNc)])
(7)
在复杂的载机平台飞行环境中,载机飞行速度v和偏航角θp的估计会存在误差,假设估计出的载机飞行速度和偏航角的误差范围为Δv和Δθp,即估计的载机速度ve∈[v-Δv,v+Δv]和偏航角θe∈[θp-Δθp,θp+Δθp]。设计一系数矩阵,使相邻脉冲间的杂波数据之差的能量在误差范围内积分最小,即
(8)
(9)
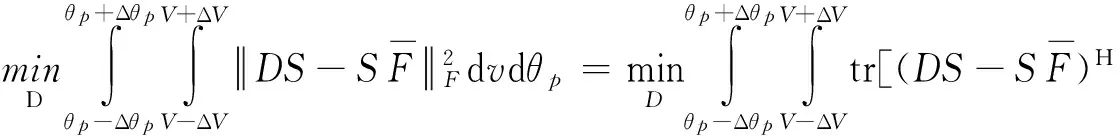
(10)
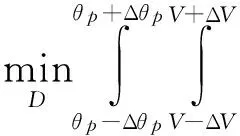
(11)
对一个CPI内的回波进行杂波抑制

(12)

3 杂波预滤波级联降维空时自适应方法
杂波相消器可以作为杂波预滤波器使用,后续处理可以级联降维空时自适应处理方法,下面将以因子法(FactoredApproach,FA)为例说明。
将系统在一个CPI内所有N个阵元接收的数据排成一个列向量
x=[x1,1,x1,2,L,x1,N,x2,1,L,xK,N]T
(13)
定义目标导向矢量为
s=st⊗ss
(14)
其中,st为目标信号的时域导向矢量;ss为目标信号的空域导向矢量。杂波预滤波器可以写成一个预滤波矩阵的形式,定义杂波预滤波矩阵为
(15)
则经过预滤波后的数据矢量和目标为
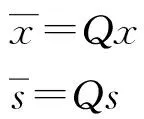
(16)
需要注意的是,经过预滤波后的信号由原来的NK维变为N(K-1)维,即经过预滤波后的数据在脉冲维上减少了一维,这是因为其中有一个脉冲用于了杂波对消。假设fk为待检测通道多普勒频率,则多普勒滤波器向量为fk=[1,exp(j2πfk),…,exp(j2π(K-2)fk)]T,降维矩阵TFA=fk⊗I。对预滤波后数据和目标进行降维处理,得到
(17)
则预滤波后因子法的权矢量为
(18)
4 实验结果
实验1 首先以仿真数据为例来验证算法的性能。实验采用8×8的平面阵,一个相干处理间隔内的脉冲数K=16,发射脉冲重复频率fr=2 000 Hz。飞行高度ha=9 km,阵元间距d=0.1 m,发射波长λ=0.2 m,载机飞行速度va=100 m/s。沿着方位角将一个距离单元等间隔的划分为个杂波散射单元。杂噪比CNR=60 dB。动目标的多普勒频率为fdt=0.15fr,信噪比SNR=10 dB。而由于地面因素干扰,造成杂波内部运动,从而造成杂波谱一定程度的展宽,这里假设杂波相对带宽Br=0.02。
图2展示了正侧视机载相控阵雷达运动平台分别使用TDPC和RTDPC,在载机速度和偏航角与实际值失配情况下,抑制杂波前后的空时二维杂波功率的变化。假设载机速度的误差为Δv=5 m/s,偏航角的误差Δθp=5°。从图2(a)中可以看出,在方位角-多普勒平面上,正侧视情况下的空时二维杂波功率沿斜率为1的迹线分布,主杂波区功率高出非杂波区约50 dB,高出信号功率30 dB。图2(b)展示了在不准确的先验知识下TDPC预滤波的效果,杂波和目标信号的能量都受到了抑制,但目标信号的能量仍然在杂波主瓣的能量之下,对比文献[10]中TDPC的预滤波效果,这说明了不准确的先验知识严重影响了TDPC抑制杂波的性能。而图2(c)展示了在参数误差范围内积分的 RTDPC预滤波效果,可以看出,经过滤波后的杂波能量明显降低,而目标信号的信噪比仍然保持在10 dB,明显超过杂波主瓣能量,为后续的动目标信号的相干积累和检测提供了方便。
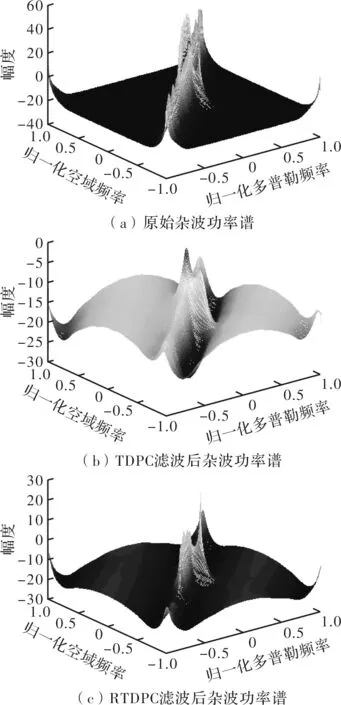
图2 预滤波处理前后杂波功率谱的空时二维分布
图3比较了EFA,TDPC预滤波级联EFA和RTDPC预滤波级联EFA算法的改善因子曲线。TDPC+EFA和RTDPC+EFA分别表示TDPC预滤波后级联EFA和RTDPC预滤波后级联EFA。从图中可以看出经过杂波预滤波后,TDPC+EFA和RTDPC+EFA在旁瓣杂波区的改善因子性能较原EFA算法有大约2dB的提升,而在主杂波区,由于TDPC预滤波矩阵的参数存在误差,TDPC+EFA算法对主杂波的抑制性能明显降低,而RTDPC+EFA在主杂波区仍然能形成很深的凹口抑制主杂波。图4给出了归一化多普勒频率fnd=0.1处的RTDPC+EFA的改善因子随载机速度的误差Δv变化的曲线。在Δv从5m/s变化到50m/s的过程中,改善因子在Δv=25m/s处最高,从此处以后开始迅速下降。
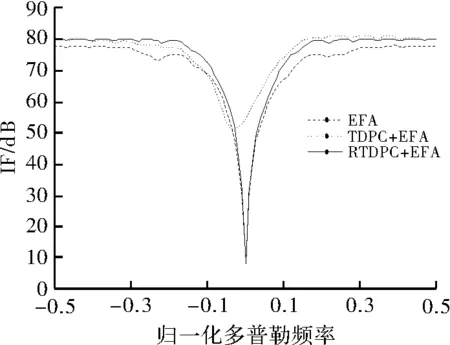
图3 预滤波前后的STAP算法改善因子曲线
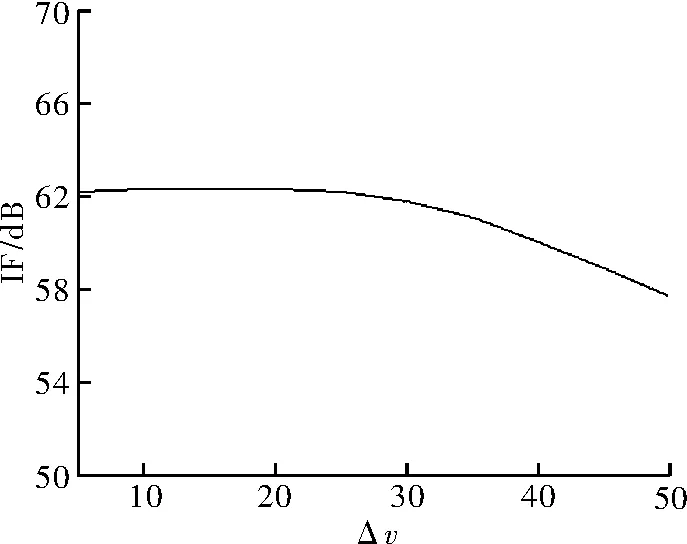
图4 改善因子随Δv变化曲线
实验2MCARM数据是美国90年代为研究STAP及其相关技术而实际录取的一批机载雷达数据,基本反映了机载雷达真实的工作环境[11]。实验中用于计算预滤波器矩阵的参数为:雷达工作波长λ=0.241 9m,阵元间距d=0.109 2m,载机速度v=100.2±5m/s,脉冲重复频率fr=1 984Hz,偏航角为φp=7.28°±5°。为方便计算,选取360~450号距离门上11个子阵的前16个脉冲数据。在405号距离单元注入一目标信号,其多普勒频率为fd=-0.157 fr,方位角为90°,信杂噪比为-36dB。图5(a)为FA,TDPC预滤波级联FA和RTDPC预滤波级联FA算法在目标所在多普勒通道各距离单元的归一化输出功率曲线。动目标检测性能用目标信号功率高出平均背景剩余杂波功率的值(RARCP)来衡量,三种方法均能将动目标检测出来,其中FA算法的RARCP约为17.87dB,虽然参数存在误差,但是TDPC+FA算法中的RARCP约为18.53dB,仍比原FA的检测性能优异。在将参数误差加入到预滤波器矩阵的设计之中后,RTDPC+FA算法中的RARCP约为20.06dB,较FA有6.19dB的性能改善,较TDPC+FA也有5.53dB的性能改善。同样,在图5(b)中,EFA,TDPC+EFA和RTDPC+EFA算法的RARCP分别为25.26dB,24.83dB和27.12dB。可以看到,在存在参数误差的情况下,TDPC+EFA的动目标检测性能反而不如EFA算法,而尽管随着自适应自由度的增加,EFA算法已经有较充足的自由度来抑制多普勒处理后的残余杂波,但RTDPC+EFA的RARCP较EFA仍有2.06dB的性能改善。
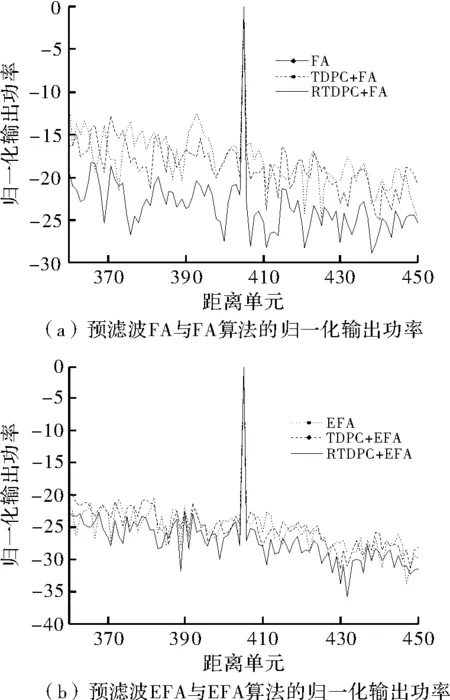
图5 预滤波处理前后归一化输出功率
5 结束语
本文提出RTDPC将载机速度和偏航角误差也作为先验知识加入到滤波器系数中,这样即使是不准确的载机速度和偏航角也不会影响RTDPC抑制杂波的能力,进一步提高了TDPC在实际工作中的稳健性。仿真实验验证了该方法在雷达系统参数存在误差的情况下也能够有效的抑制杂波,用该方法作为传统空时自适应处理算法的预滤波器,后续空时自适应处理算法的性能也会得到改善。
[1]KlemmR.AdaptiveairborneMTI:anauxiliarychannelapproach[J].IEEEProceedingF,1987,134(3):269-276.
[2]SkolnicMI.Radarhandbook[M].SecondEdition.NewYork:McGraw-Hill,1990.
[3]BrennanLE,ReedIS.Theoryofadaptiveradar[J].IEEETransactionsonAES,1973,9(2):237-252.
[4]ReedIS,MalletJD,BrennanLE.Rapidconvergencerateinadaptivearrays[J].IEEETransactionsonAES,1974,10(6):853-863.
[5] 保铮,廖桂生,吴仁彪,等.相控阵机载雷达杂波抑制的时空维自适应滤波[J].电子学报,1993,21(9):1-7.
[6]WangH,CaiL.Onadaptivespatial-temporalprocessingforairbornesurveillanceradarsystems[J].IEEETransactionsonAerospaceElectronicsSystems,1994,30(3):660-669.
[7]KlemmR.Space-timeadaptiveprocessing—principlesandapplications[M].London:TheInstituteofElectricalEngineers,1998.
[8] 吕维,王志杰,李建辰,等.空时耦合项对空时自适应处理的影响[J].西安电子科技大学学报,2012,39(2):207-212.
[9] 吕晖,冯大政,和洁,等.机载多输入多输出雷达局域化降维杂波抑制方法[J].西安电子科技大学学报,2011,38(2):88-92.
[10]李晓明,冯大政,刘宏伟,等.相控阵机载雷达空时两维杂波预滤波处理方法[J].西安电子科技大学学报,2008,35(2):216-222.
[11]SureshBabuBN,TorresJA,MelvinWL.Processingandevaluationofmultichannelairborneradarmeasurements(MCARM)measureddata[C].ProceedingsofIEEEInternationalSymposiumonPhasedArraySystemsandTechnology,1996:395-399.
A Robust Two-Dimensional Pulse-to-pulse Canceller of Ground Clutter
XUE Haiwei,FENG Dazheng,ZHOU Yan
(National Key Laboratory of Radar Signal Processing,Xidian University,Xi’an 710071,China)
The two-dimensional pulse-to-pulse canceller (TDPC) of ground clutter can effectively pre-filter the clutter along the clutter trace and enhance the moving target’s detectability of the following space-time adaptive processing algorithms.However,the inaccurate radar system parameters,especially the airborne velocity and drift angel,will constrain the TDPC’s clutter suppression ability.To solve this problem,a robust two-dimensional pulse-to-pulse canceller (RTDPC) of ground clutter is proposed,in which the errors of the airborne velocity and drift angel are taken as the priori knowledge and added into the design of filtering coefficient matrix.The simulated and MCARM real data are utilized to verify the validity of the proposed method.The experimental results show that the clutter suppression performance of RTDPC can be improved compared with the TDPC under the condition for inaccurate airborne velocity and drift angle.The moving target detectability of following space-time adaptive processing algorithms is also enhanced after RTDPC is used as a pre-filter.
space-time adaptive processing (STAP);pre-filter;clutter suppression
2014- 09- 12
国家自然科学基金资助项目(61271293)
薛海伟(1985—),男,博士研究生。研究方向:干涉SAR数据处理,SAR成像,盲信号处理。E-mail:xuehw001@gmail.com。冯大政(1959—),男,教授,博士生导师。研究方向:雷达成像,阵列信号处理,盲信号处理,神经网络等。周延(1987—),男,博士研究生。研究方向:阵列信号处理。
10.16180/j.cnki.issn1007-7820.2015.05.014
TN97
A
1007-7820(2015)05-045-05

