高频谐波振动冲击破岩机制及试验分析
李思琪,闫 铁,李 玮,卢亚涛,李显义
(1.东北石油大学石油工程学院,黑龙江大庆163318;2.中国石油大庆油田第六采油厂,黑龙江大庆163114;3.中国石油钻井工程技术研究院,北京102206)
高频谐波振动冲击破岩机制及试验分析
李思琪1,闫 铁1,李 玮1,卢亚涛2,李显义3
(1.东北石油大学石油工程学院,黑龙江大庆163318;2.中国石油大庆油田第六采油厂,黑龙江大庆163114;3.中国石油钻井工程技术研究院,北京102206)
基于振动学理论,建立高频谐波振动冲击破岩的物理模型和数学模型,应用MATLAB软件对数学模型求解,分析各参数对简谐振动激励下岩石振动的影响,并通过室内试验进一步验证高频谐波振动冲击钻井技术的破岩效果。结果表明:在简谐振动激励下,机械钻速比常规钻井提高了13.2%;岩石刚度、阻尼、临界力与机械钻速呈反比,动态激振力与机械钻速呈正比,激励频率与岩石固有频率越接近,机械钻速越大;机械钻速随着钻压、转速的增加而增加。
高频谐波振动冲击;破岩模型;因素分析;室内试验
在石油行业钻井过程中,冲击破岩一直是岩石破碎的主要形式[1-3]。随着深部地层勘探开发比例逐年增加,复杂地层与难钻地层钻遇率升高,现有技术已不能满足当今钻井作业需求,亟须发展新的高效破岩技术解决当前钻井作业难题[4-6]。高频谐波振动冲击钻井技术是一种新的高效破岩技术[7-8]。国内外一些学者对其钻进机制、破岩效果和频率特征等内容进行了一系列的探索研究[9-12]。李玮等[13]研究了谐波振动激励下钻具的破岩机制并进行了相应的试验分析。李思琪等[14]基于最小作用量原理,建立了岩石的微振动方程,分析了冲击频率、冲击力等因素对岩石振动的影响。杨威等[15]展开了共振碎岩机制、孔隙介质对共振破岩过程的影响等方面的探索。Wiercigroch[16]申请了共振增强钻井的发明专利,发明了一种可以实现共振钻井的装置与方法。目前,高频谐波振动冲击破岩技术仍处于室内研究阶段,无论是理论研究还是技术应用都存在很大的发展和提升空间。笔者基于振动学理论,建立高频谐波振动冲击钻井的物理模型和数学模型,应用MATLAB软件对数学模型求解,分析各参数对简谐振动激励下岩石振动的影响,通过室内试验进一步验证高频谐波振动冲击钻井技术的破岩效果。
1 高频谐波振动冲击破岩模型
1.1 物理模型
高频谐波振动冲击破岩系统由3个质量系统组成,其中钻头、激励器质量分别为m1、m2,振动质量为m3。钻头与激励器之间通过刚度为k2,阻尼系数为c2的弹簧相连,激励器与振动质量之间通过刚度为k3,阻尼系数为c3弹簧相连。激励器上施加的静载为Fs,钻头上施加的动载为Fcos(ωt+φ)。钻头初始位置离岩石表面的距离为G。岩石由黏弹性滑块模拟,刚度为k1的弹簧和阻尼系数为c1的阻尼器分别用以考虑岩石的弹性行为和阻尼。当钻头作用于岩石表面上的作用力Pc超过滑块的临界力Pr时,滑块开始向下运动,从而模拟系统的钻进。钻头和激励器的位移分别为x1、x2,振动质量的位移为x3,岩石表面的位移为xt,滑块的位移为xb,如图1所示。
1.2 数值模型
根据物理模型,分析各部分模块的运动状态。振动质量m3的运动方程为

激励器m2的运动方程为

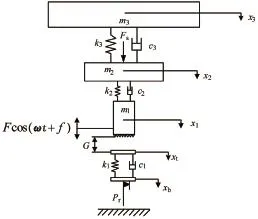
图1 高频谐波振动冲击破岩模型Fig.1 Rock breaking model of high frequency harmonic vibration impacting
钻头有3种不同的运动状态,分别为与岩石没有接触的运动,与岩石接触但不发生钻进的运动以及钻进岩石的运动。
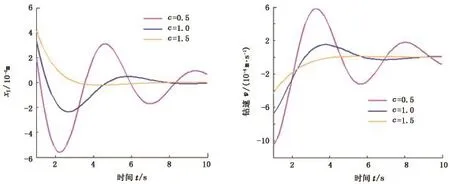
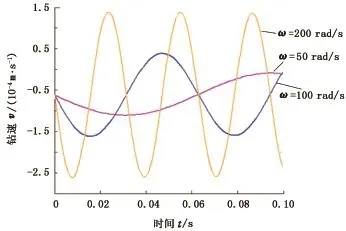
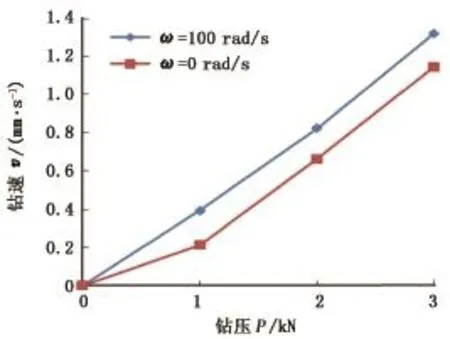
(1)当x1 这个阶段岩石表面的作用力Pc为 钻头、岩石表面以及滑块的运动方程为 钻头持续向下运动,当到达岩石表面时,即x1= xt+G时,进入下一个运动阶段。 式中,Pr为滑块的临界力,N。 岩石表面的作用力Pc为 钻头、岩石表面以及滑块的运动方程为 当岩石表面的作用力大于滑块的临界力时,即Pc大于、等于Pr时,进入下一个破岩钻进阶段。 该阶段岩石表面的作用力Pc等于阻力Pr,即 钻头、岩石表面以及滑块的运动方程为 该过程一直持续到作用于岩石表面的作用力Pc小于临界阻力Pr时,第三阶段结束,系统再次开始第二阶段的运动。 1.3 简化模型 为了进一步分析钻头与岩石之间的相互作用,将高频谐波振动冲击破岩模型简化,分析钻头与模拟岩石的黏弹性滑块之间的运动行为。物理模型如图2所示。 图2 钻头与岩石相互作用的简化破岩模型Fig.2 Simplified rock breaking model between drill bit and rock 系统的运动方程可以简化为 应用MATLAB软件对式(6)进行数值求解,分析单个冲击频率下岩石在不同阶段的运动状态以及岩石刚度、阻尼、冲击频率等参数对钻头下岩石振动的影响。 2.1 钻头与岩石未接触时岩石的运动状态 当k1(xt-xb)<0时,钻头与岩石不发生接触,即钻头不发生钻进,此时岩石表面与滑块之间的距离xt-xb为恒定的常数,由岩石的刚度k和岩石的阻尼c决定,因此岩石的振动位移随时间的变化曲线为一条直线,如图3所示,其中岩石1、岩石2及岩石3分别为砂岩、石灰岩及花岗岩。 图3 不同岩石表面位移随时间的变化Fig.3 Changes of vibration displacement of different rocks with time 2.2 钻头与岩石接触但不钻进时岩石的运动状态 当0 2.2.1 刚度对岩石振动的影响 图4给出了不同刚度下岩石表面振动位移、振动速度随时间变化的关系曲线。由图4可知,在简谐振动冲击下,岩石也呈现简谐振动的趋势。岩石的刚度越小,岩石能够达到的最大振动位移和最大振动速度越大。这是由于在简谐激励力相同和岩石质量相同的条件下,岩石刚度越小,岩石越易产生变形,也越易产生振动。同时,由于阻尼的存在,岩石的振动随时间不断衰减。 2.2.2 阻尼对岩石振动的影响 图5为不同阻尼下岩石表面的振动位移、振动速度随时间变化的关系曲线。由图5可知,岩石的阻尼越小,岩石表面产生的振动幅度越大,振动速度也越大,并且振动维持的时间越长。当岩石阻尼系数达到1.5时,系统处于过阻尼状态,此时钻头对岩石的冲击能量大部分被阻尼所消耗,因此岩石几乎不产生简谐振动。 图4 不同刚度下岩石表面振动位移、振动速度随时间的变化Fig.4 Changes of vibration displacement and vibration velocity of rock with time in different k 图5 不同阻尼下岩石表面振动位移、振动速度随时间的关系曲线Fig.5 Changes of vibration displacement and vibration velocity of rock with time in different c 2.2.3 激励频率对岩石振动的影响 图6 不同动态激励频率下岩石振动速度与时间的关系Fig.6 Changes of vibration velocity of rock with time in different ω 图6为不同动态激励频率下岩石振动速度随时间的变化。由图6可知,岩石的振动速度随激励频率变化呈简谐变化。不同的激励频率下,岩石所能达到的最大振动速度不同,这与岩石的固有频率有关。当激励频率与岩石的固有频率越接近时,岩石产生的振动位移越大,振动速度也越大。当激励频率与岩石固有频率相等时,岩石达到共振,相应的振动位移和速度达到峰值。 2.2.4 动态激振力对岩石振动的影响 图7 不同动态激振力下岩石振动速度与时间的关系Fig.7 Changes of vibration velocity of rock with time in different F 图7为不同动态激振力下岩石振动速度与时间的关系曲线。由图7可见,岩石的振动速度随着简谐振动冲击力呈周期性变化。在相同激励频率下,岩石的振动速度随动态激振力的增加而增加。激振力越大,岩石所能达到的最大振动速度也越大。 2.3 钻头钻进时岩石的运动状态 当k1(xt-xb)>Pr时,钻头进入钻进阶段。在这个阶段,作用于岩石表面的简谐振动冲击力大于岩石的临界力,岩石发生塑性变形,岩石表面与滑块均产生振动位移,振动位移受岩石阻尼和临界力的影响,并随时间的改变而改变。 图8为不同阻尼、临界力下岩石表面运动位移随时间的变化。由图8可知,岩石阻尼越小,岩石随时间生产的振动位移越大,这种运动一直持续到冲击能量全部被消耗,岩石表面停止运动。岩石阻尼较大时,岩石发生塑性变形,产生的运动位移非常微小。 临界力越小的岩石,越容易达到其塑性变形的条件,越容易产生大幅度的运动位移。反之,岩石产生的振动位移越小,直到冲击力不再达到岩石的临界力,滑块停止运动。 图8 不同阻尼、临界力下岩石表面运动位移随时间的变化Fig.8 Changes of vibration displacement of rock with time in different c and Pr 为了进一步证明理论模型与影响因素分析的准确性,采用室内试验进行验证。试验装置为东北石油大学“高效钻井破岩技术”研究室自主研发的“岩石振动激励模拟测试系统”,如图9所示。 图9 岩石振动激励模拟测试装置示意图Fig.9 Schematic diagram of rock vibration excitation simulation test device 完整的试验系统由主体机架、岩样夹持机构、高频振动发生装置、钻进系统、旋转装置、钻压模拟控制系统、数据采集控制系统等部分构成。其功能主要是产生各种振动激励,如低频大振幅和高频小振幅的振动激励,并在岩石稳态响应振动条件下分析钻头的旋转破岩机理。 分别对砂岩和花岗岩进行相同条件下的简谐振动冲击,试验结果如图10所示。 图10 砂岩和花岗岩的钻进曲线Fig.10 Progression curves of sandstone and granite 由图10可知,在相同的简谐振动冲击下,等时间内砂岩钻进的深度高于花岗岩,同比节约钻进时间约30%。这是由于砂岩相比于花岗岩,岩石刚度小,产生破坏所需临界力小,因此在简谐振动冲击下,机械钻速高于花岗岩。 分别对砂岩进行有、无简谐振动冲击的钻进试验,试验结果如图11所示。 图11 不同激励频率下砂岩钻速与钻压的关系Fig.11 Relationship between drilling rate and drilling pressure of sandstone in different ω 由图11可知,随着钻压增加,有、无简谐振动冲击的钻头的机械钻速均近似呈线性增加。但在简谐振动冲击下,钻头的钻进速度高于常规钻井条件下的机械钻速,平均增加幅度为13.2%,这说明简谐振动冲击可以提高钻头的钻进速度。当简谐振动冲击频率与岩石的固有频率相同时,将大幅度提高岩石的破坏速率。 分别对砂岩施加1、2 kN的动态激振力,钻进结果如图12所示。 图12 不同动态激振力下砂岩钻速与转速的关系Fig.12 Relationship between drilling rate and rotation rate of sandstone in different F 由图12可知,简谐振动激励下,钻头的钻进速度随转速的增加而增加。对岩石施加相同的激励频率而改变动态激励振幅时,动态激励振幅越大,钻头的钻进速度也越大,最大增加幅度达51%。 (1)岩石在简谐振动激励下产生振动,其振动状态受岩石刚度、阻尼、临界力,动态激振力与激励频率等因素影响。 (2)在钻头与岩石接触但不发生钻进时,岩石的振动随简谐振动冲击呈现谐波振动。岩石的刚度越小,阻尼越小,激励频率越接近岩石固有频率,动态激振力越大,其振动位移和振动速度越大。 (3)在钻头钻进岩石阶段,岩石阻尼越小,临界力越小,岩石越易产生塑性破坏,振动位移近似线性变化。 (4)简谐振动冲击可以提高钻头的钻进速度,机械钻速随着钻压和转速的增加而增大。 [1] 邹德永,蔡环.布齿参数对PDC钻头破岩效率影响的试验[J].中国石油大学学报:自然科学版,2009,33(5):76-79. ZOU Deyong,CAI Huan.Experiment on effect of cutter parameters of PDC bit on rate of penetration[J].Journal of China University of Petroleum(Edition of Natural Science),2009,33(5):76-79. [2] 常德玉,李根生,沈忠厚,等.射流冲击载荷对井底岩石应力场的影响[J].中国石油大学学报:自然科学版,2011,35(2):74-79. CHANG Deyu,LI Gensheng,SHEN Zhonghou,et al. Influence of water jet impact load on bottom hole rock stress field[J].Journal of China University of Petroleum(Edition of Natural Science),2011,35(2):74-79. [3] 马清明,王瑞和.PDC切削齿破岩受力的试验研究[J].中国石油大学学报:自然科学版,2006,30(2):45-47. MA Qingming,WANG Ruihe.Experimental study on force of PDC cutter breaking rock[J].Journal of China University of Petroleum(Edition of Natural Science),2006,30(2):45-47. [4] 常德玉,李根生,沈忠厚,等.深井超深井井底应力场[J].石油学报,2011,32(4):697-703. CHANG Deyu,LI Gensheng,SHEN Zhonghou,et al. The stress field of bottom hole in deep and ultra-deep wells[J].Acta Petrolei Sinica,2011,32(4):697-703. [5] 曾义金,刘建立.深井超深井钻井技术现状和发展趋势[J].石油钻探技术,2005,33(5):1-5. ZENG Yijin,LIU Jianli.Technical status and developmental trend of drilling techniques in deep and ultra-deep wells[J].Petroleum Drilling Techniques,2005,33(5):1-5. [6] 王大勋,刘洪,韩松,等.深部岩石力学与深井钻井技术研究[J].钻采工艺,2006,29(3):6-10. WANG Daxun,LIU Hong,HAN Song,et al.Deep rock mechanics and deep or ultra deep well drilling technology[J].Drilling&Production Technology,2006,29(3):6-10. [7] 李玮,闫铁,张志超,等.高频振动钻具冲击下岩石响应机理及破岩试验分析[J].石油钻探技术,2013,41(6):25-28. LI Wei,YAN Tie,ZHANG Zhichao,et al.Rock response mechanism and rock breaking test analysis for impact of high frequency vibration drilling tool[J].Petroleum Drilling Techniques,2013,41(6):25-28. [8] WIERCIGROCH M,WOJEWODA J.Vibrational energy transfer via modulated impacts for percussive drilling[J]. Journal of Theoretical and Applied Mechanics,2008,46(3):715-726. [9] 刘虎,张卫红,朱继宏.简谐力激励下结构拓扑优化与频率影响分析[J].力学学报,2013,45(4):588-597. LIU Hu,ZHANG Weihong,ZHU Jihong.Structural topology optimization and frequency influence analysis under harmonic force excitations[J].Chinese Journal of Theoretical and Applied Mechanics,2013,45(4):588-597. [10] 邱兆国,吴斌,何存富.弱黏接结构中谐振频率与刚度比的数值研究[J].工程力学,2012,29(6):32-46. QIU Zhaoguo,WU Bin,HE Cunfu.Numerical anslysis of resonance frequency and stiffness ration in weak bonded structures[J].Engineering Mechanics,2012,29(6):32-46. [11] AGUIAR R R,WEBER H I.Development of a vibcompact device for the resonance hammer drilling:proceedings of the XII International Symposium on Dynamic Problems of Mechanics[C].Brazil:ABCM,2007. [12] OSTASEVICIUS V,GAIDYS R,RIMKEVICIENE J,et al.An approach based on tool mode control for surface roughness reduction in high-frequency vibration cutting[J].Journal of Sound and Vibration,2010,329:4866-4879. [13] LI Wei,YAN Tie,LI Siqi,et al.Rock fragmentation mechanisms and an experimental study of drilling tools during high-frequency harmonic vibration[J].Petroleum Science,2013,10(2):205-211. [14] 李思琪,闫铁,王希军,等.基于最小作用量原理的岩石微振动方程及分析[J].石油钻探技术,2014,42(3):66-70. LI Siqi,YAN Tie,WANG Xijun,et al.The micro vibration equation of rock and its analysis basing on the principle of least action[J].Petroleum Drilling Techniques,2014,42(3):66-70. [15] 杨威,李磊,赵延旭,等.共振碎岩理论的初步探究[J].能源技术与管理,2007(4):7-9. YANG Wei,LI Lei,ZHAO Yanxu,et al.Preliminary inquiry of theory of resonance rock breaking[J].Energy Technology and Management,2007(4):7-9. [16] WIERCIGROCH M.Resonance enhanced drilling:method and apparatus:US,319994[P].2010-12-23. (编辑 沈玉英) Mechanism experimental study of rock breaking assisted with high frequency harmonic vibration and impaction LI Siqi1,YAN Tie1,LI Wei1,LU Yatao2,LI Xianyi3 A new and efficient rock breaking technique assisted with high frequency harmonic vibration and impaction was developed for drilling in complicated and hard formations.In this study,physical and mathematical simulation models were established to study the process rock breaking based on the theory of vibration.The mathematical model was solved by the MATLAB software,and the effects of various parameters on rock vibration under the harmonic vibration excitation were analyzed.The effect of the vibration and impaction technique on rock breaking has been verified through indoor experiments. The experimental results show that the penetration rate under the harmonic vibration excitation is increased by 13.2%.The penetration rate increases with the increase of the dynamic excitation force,while rock's stiffness,damping and critical force have a negative effect on penetration rate.The more closer between the excitation frequency and the natural frequency of rock,the greater the penetration rate is.Nevertheless,the penetration rate also increases with the increasing of the weight on bit and rotation speed. high frequency harmonic vibration;rock breaking model;factor analysis;indoor experiment TE 21 A 1673-5005(2015)04-0085-07 10.3969/j.issn.1673-5005.2015.04.011 2014-12-11 国家自然科学基金重大项目(51490650);国家自然科学基金项目(51274072);东北石油大学研究生创新科研项目(YJSCX2014-011NEPU) 李思琪(1989-),女,博士研究生,研究方向为岩石力学和高效破岩技术。E-mail:lisiqi448@163.com。 引用格式:李思琪,闫铁,李玮,等.高频谐波振动冲击破岩机制及试验分析[J].中国石油大学学报:自然科学版,2015,39(4):85-91. LI Siqi,YAN Tie,LI Wei,et al.Mechanism experimental study of rock breaking assisted with high frequency harmonic vibration and impaction[J].Journal of China University of Petroleum(Edition of Natural Science),2015,39(4):85-91.

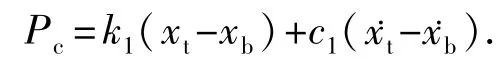





2 高频谐波振动冲击钻井模型影响因素分析




3 试验装置及测试系统

4 试验结果及分析


5 结 论
(1.Institute of Petroleum Engineering,Northeast Petroleum University,Daqing 163318,China;2.The Sixth Oil Production Plant of Daqing Oilfield,PetroChina,Daqing 163114,China;3.Drilling Research Institute,PetroChina,Beijing 102206,China)

