基于自适应迭代学习控制的工作艇收放装置主动减摆策略研究
高云剑,史洪宇
(1.海装上海局综合计划处,上海 201210;2.哈尔滨工程大学,黑龙江 哈尔滨 150001)
基于自适应迭代学习控制的工作艇收放装置主动减摆策略研究
高云剑1,史洪宇2
(1.海装上海局综合计划处,上海 201210;2.哈尔滨工程大学,黑龙江 哈尔滨 150001)
工作艇收放装置主要用于完成快速、安全地将舰船上的小艇及人员移至水面,或安全回收工作艇至舰船上等海上任务。针对这一典型的欠驱动机械系统,采用拉格朗日方程的方法建立其动力学模型。根据舰船在海上的实际运动情况,对系统的二维动力学模型进行描述,分析小艇摇摆的二维平面摆角,研究其在船体运动影响下的变化情况。然后在上述非线性动力学模型的基础上,针对系统的摆动部分,为其设计自适应迭代控制闭环控制器,达到消摆的目的。最后,仿真结果证明了此控制方法的有效性。
工作艇收放装置;动力学模型;拉格朗日方程;部分反馈线性化;自适应迭代学习控制
0 引言
工作艇收放装置广泛应用于各类水面舰船上,主要用于收放海上作业艇或救生艇。由于风、浪、流等海上各类复杂环境因素的影响,安装于舰船一侧的工作艇在其收放过程中不可避免的要呈现“摆动”运动,这就成为了影响海上作业快速性及安全性的关键因素。当艇的摆动幅度过大时,极有可能造成船用设备损坏或工作人员伤亡等一系列严重后果。为解决这一问题,提出一套有效的、适合当前海况的减摆策略十分必要。
工作艇收放装置属于船用起重机的一种,其运动较车间、码头等工业场所的吊车更复杂,自由度更多,所以减摆控制策略的研究方面也需要考虑更多的影响因素。目前,国内外关于船上吊车的研究较少,大多数研究是把负载的摆动当成吊车动力学中的非线性问题来分析。Y.Sakawa[1-3]是最早研究回转式挺杆起重机的,他采用基于LQR设计的最优控制器来控制吊车的回转、俯仰和起升运动,以达到消除负载的摆动的目的。随着非线性理论的日益发展,Eling和Mc Clinton最先讨论了回转式挺杆起重机的非线性动力学问题的,通过对系统进行建模和数值仿真,提出了谐振状态下负载摆动的运动方程。Yoshida和Kawabe、Nguyen则分别提出了起重机的实时饱和控制策略和状态反馈控制方法。而Chin等人在文献[4]中建立了一个三维的非线性船上吊车绳-摆系统模型,并研究了在悬臂顶端的激励和参数变化下系统模型的动态特性。Masoud[5]也对船上吊车的减摆控制进行了较为深入的研究,提出了很多种建设性的方法,其研究的系统模型的稳定性已经得到了证明。国内对此类研究开展得较晚,特别针对船上吊车这类回转式挺杆起重机减摆控制的研究几乎没有,少数学者的研究集中在回转塔式起重机的减摆控制上。董明晓等人[7]建立了回转塔式起重机的载荷摆动模型,并对模型线性化和起升运动引起的误差进行了分析。
首先,本文基于拉格朗日方程建立了工作艇收放装置的非线性动力学模型,该模型描述了收放装置以及工作艇的运动情况。然后,对上述模型进行部分反馈线性化并解耦控制量,给出非线性解耦的基于自适应迭代学习控制的闭环控制策略,实现对欠驱动系统中未驱动部分的减摆控制,在最短时间内消除小艇摆动角,这是本文的研究重点。最后,对整个模型进行了数字仿真实验研究并进行总结,由仿真结果验证该控制方法的有效性。
1 工作艇收放装置的动力学建模
收放装置起吊点与小艇采用柔性钢绳联结,故存在惯性。忽略风载等外界干扰的情况下,艇的摇摆可以看作以吊点为中心,以起升绳长为半径做球冠面运动。由于船舶横摇、纵摇对摆动的影响类似,可将绳索在三维空间的二自由度摆角看作横、纵摇平面内的单摆运动的复合运动,这里仅取横摇平面内的运动进行研究,基于此,建立摆角的二维动力学模型。
1.1 二维动力学模型坐标系的建立
研究二维模型,须定义小艇在惯性空间的位置。建立横摇平面内的船、收放装置及工作艇各自的参考坐标系,坐标系分布如图1所示:
1)惯性坐标系OXY:
定系,各轴与原点均无运动,OX轴水平向右,OY轴铅垂向上。
2)船体坐标系O0X0Y0:
O0点与船体几何中心位置重合,O0X0轴水平向右为正,O0Y0轴垂直于O0X0轴向上为正。该坐标系用于确定横摇时船体的方位。在船舶静止情况下,船体坐标系与地面惯性坐标系完全重合。
3)起吊点坐标系B-xByB:
B是吊臂起吊点,B系是由船体坐标系O0X0Y0,分别沿O0X0方向和O0Y0方向平移得到的,各轴的方向同上。
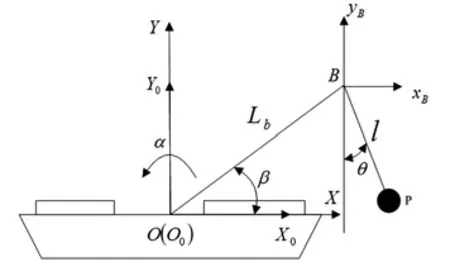
图1 各坐标系位置及方向示意图
1.2 二维动力学模型的确定
设船舶-收放装置的整体和小艇的质量分别为m1、m2,吊臂长Lb,绳索的长度为l,β为吊臂与船体坐标系横轴之间的夹角,α为船横摇的角度。设船体逆时针转动的方向为正方向,θ为小艇的摆动角。
当横摇角不大时,船舶在规则波中的横摇为周期运动,可由如下方程描述:

式中:φA为横摇幅值,rad;ω为横摇角频率,rad/s;δ为横摇运动与波浪扰动力矩之间的相位角,rad。
由于收放装置基座与船甲板固连,二者均为刚体,故起吊点B的运动轨迹方程可由上式得出:

式中:a为B点的摆动幅值,m。
将B点的运动轨迹方程表示为OX,OY轴上的分量形式,示意图如图2,表达式如下(设顺时针方向转动):
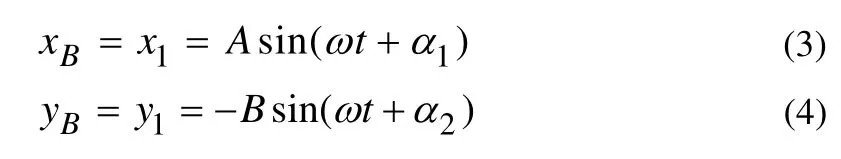
式中:A为横摇幅值a在OX轴上的分量,m;B为横摇幅值a在OY轴上的分量,m。

图2 对起吊点B运动轨迹函数的分解示意图
再由图1中所示的位置关系得到艇在惯性坐标系中的位置坐标为:

分别选取x、y、θ、l为广义坐标,由拉格朗日方程,得到系统的二维动力学模型

将其写成标准矩阵形式如下:

式中:q表示系统的状态;M(q)表示系统的惯量矩阵;D表示系统的阻尼矩阵;C(q)表示系统的科里奥利力和离心力矩阵;g(q)表示系统的重力作用矩阵。其中:
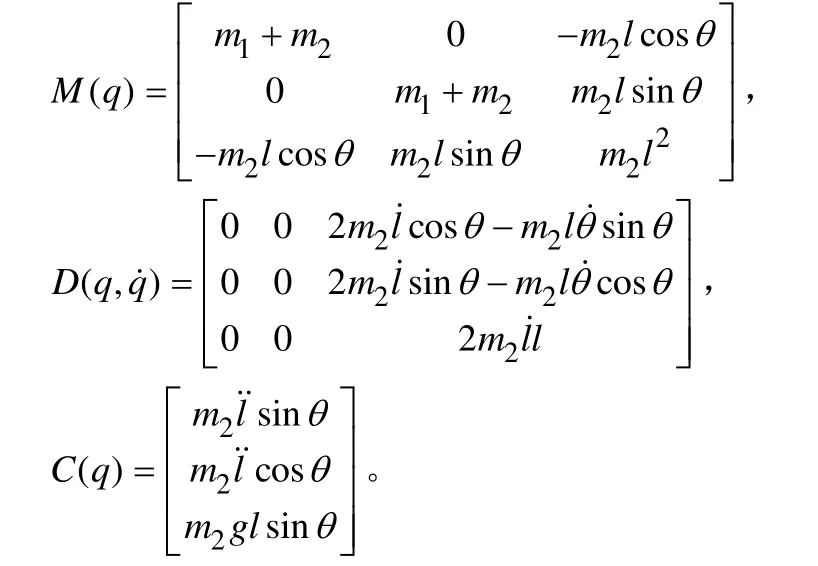
1.3 收放装置模型的部分反馈线性化
由于系统为欠驱动系统,而且非线性强耦合,不便于直接设计控制器,故先将系统的未驱动部分进行部分反馈线性化,可将式(11)写成如下形式:

系统惯量矩阵可按驱动部分与未驱动部分写为:
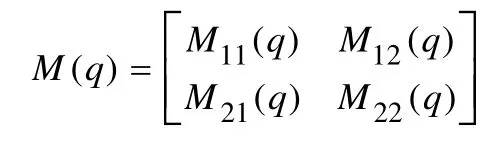
式(13)即是系统的未驱动部分。由式(12)和式(13)得出:

其中:



式(16)、(17)可化为系统对应的级联规范型,是后文设计防摆非线性控制器的基础。而欠驱动变量 θ则表征了系统的内部变化情况,控制系统的目标即为保证其稳定性。由式(9)可得出表达式

2 基于自适应迭代学习控制的轨迹跟踪防摆控制策略研究
根据前一部分对系统进行的部分反馈线性化变换,可将收放装置的状态方程写为如下形式

设计基于自适应迭代学习控制的闭环控制器。系统的输出量Ω为艇身在空间各轴上的实际位移量(x,y,z),确定驱动部分即吊臂端位置信号轨迹控制律的设计步骤如下:
设系统进行第j次迭代,由坐标变换引入吊臂端位置信号的位置跟踪误差ε1,j,即

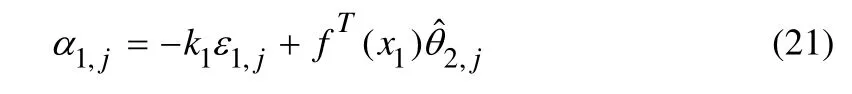
其中,k1>0,为设计参数,为θ2,j估计值。再次引入误差变量ε2,j,令

构造Lyapunov函数如下
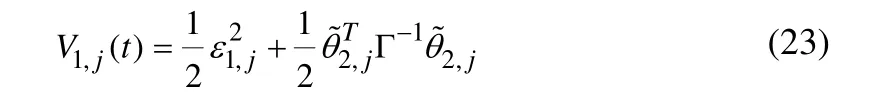


选择参数自适应律为

式(32)写为向量形式为

其中:

综合式(27)、(34),为保证第二级子系统Lyapunov函数的导数不大于零,最终设计得到第j次迭代的输入控制律和时变参数自适应律如下

其中:t∈[0,T],k1与 k2为控制器参数;估计量ˆβ-1(t)=0;q1为自适应控制律参数,且与k1,k2∈R2×2均为正定对称矩阵。综上,对于误差系统的完整Lyapunov函数可表示为:

其导数满足如下不等式:

当系统内部动态稳定时,可保证跟踪精度。
3 仿真结果
现以一收放装置系统为例进行仿真。仿真参数为:小艇质量m=3000kg,取绳长l=8m;从船体质心(即惯性系原点)到起吊点的距离用向量表示。液压缸内径 100mm,活塞杆直径为70mm。仿真步长设为100。利用Matlab/Simulink得到如下仿真结果。
3.1 收放装置被动减摆效果仿真
输入不同的正弦驱动信号,得到自由摆动时与减摆之后的摆角θ变化仿真曲线分别如图3~5所示。对比三幅图可知,随着船体横摇角幅度的逐渐增大,减摆前后的摆角幅度都有所增大,但减摆作用对频率的影响较小。综合三幅图分析可知,在加入防摆闭环控制之后,小艇摇摆角的幅值要较减摆之前出现了大幅衰减,曲线更加平滑,且频率降低、周期增大为减摆前的两倍左右。在一般情况下,系统在调整一周期后会迅速达到稳态,并始终保持小幅摆动的状态,这保证了小艇收放作业的安全性。
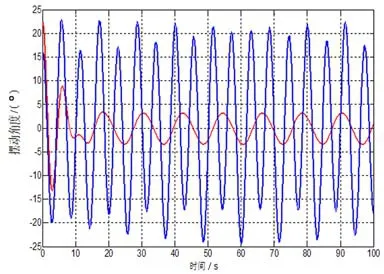
图3 横摇角12.58°,周期10s条件下减摆前后摇摆角度对比
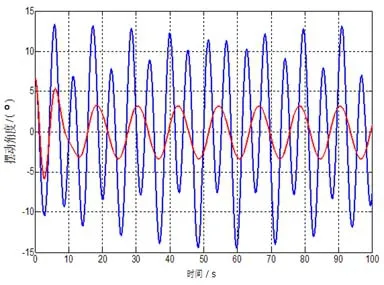
图4 横摇7.27°,周期12s条件下减摆前后摇摆角度对比

图5 横摇23°,周期12s条件下减摆前后摇摆角度对比
3.2 收放装置主动减摆效果仿真
本文的主动减摆控制策略为自适应迭代学习控制。收放装置系统参数为:母船质心距船舷的距离为6m,基座支柱高度2.5m,吊臂长度13.4m,联接机构长度为1.45m,收放装置各机构和质量m1=400kg;考虑摆长不变的情况,令 l=4m;g=9.81g/m2。为保证被控对象初始输出与指令初值一致,取系统初始状态为x(0)=[0 0]T。若仅研究横摇平面,则令θy=0。根据3.3.2节中得出的控制律与自适应律如下:

系统的欠驱动变量(即摆角)是系统的内部状态,驱动部分是系统的输出变量。控制器参数选为:各次迭代的自适应律参数均取qj=10。总迭代次数为5,仿真时间 t=100s。根据海况不同而有幅值与角频率的不等,回转轴 1与回转轴 2的位置期望轨迹设为A1sinω1t与A2sinω2t。最终可得到经主动减摆后的负载摆动效果仿真曲线如图6所示。
其中:(a) 横摇 7.27°,周期 12s;(b) 横摇 12.58°,周期14s;(c) 横摇23°,周期14s。
观察图6可看出,当输入摇摆角信号为7.27°,周期12s,闭环防摆控制下系统达到稳态时的摆角变化稳定在(-0.8°,0.8°),说明此时摆角已基本无变化,负载与绳索保持微动状态。

图6 不同条件下减摆后负载摇摆角度变化曲线
当输入摇摆角信号为12.58°,周期14s时,系统达到稳态时的摆角稳定在(-1.8°,1.8°),角度衰减率达到约 95%。当输入摇摆角信号为23°,周期 14s,闭环控制的摆角稳态幅值为(-3.8°,3.8°),角度衰减达到约90%。在3种海浪情况下,经过防摆后的摆角振荡频率都较自由振荡时大大衰减。仿真结果符合收放系统运动的特征,故证明了该动力学模型的正确性以及该控制方法的有效性。
3.3 收放装置主动减摆效果的ADAMS仿真
根据上文对控制算法的设计,使用 ADAMS作为仿真平台,对主动式减摆系统下的工作艇摆动角变化进行了仿真,随输入信号不同,各情况下的负载自由摆动以及减摆后的曲线如下:
1)输入正弦信号:横摇7.27°,周期12s,见图7~8。2)输入正弦信号:横摇13°,周期14s,见图9~10。3)输入正弦信号:横摇23°,周期14s,见图11~12。

图7 小艇自由摆动的角度变化曲线
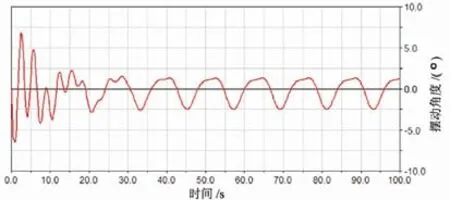
图8 主动减摆后摆角变化曲线

图9 小艇自由摆动的角度变化曲线

图10 主动减摆后摆角变化曲线

图11 小艇自由摆动的角度变化曲线

图12 主动减摆后摆角变化曲线
4 结论
本文采用拉格朗日方程建立了工作艇收放装置的二维动力学模型,更具一般性和实用性。在此非线性模型的基础上,本文给出了将欠驱动系统微分方程化为规范型的方法,并进一步提出了适合此欠驱动系统的闭环控制策略,实现了整个收放系统的防摆功能。指出运用主动防摆控制将是高海况工作艇收放装置未来发展的方向。
[1]Sakawa Y,Shindo Y,Hashimoto Y.Optimal control of a rotary crane[J].Optimization Theory and Applications,1981,15(5): 535-557.
[2]Sakawa Y,Shindo Y.Optimal control of container cranes[J]. Automatica,1982,18(3): 257-266.
[3]Sakawa Y,Nakazumi A.Modeling and control of a rotary crane[J].Dynamic Systems,Measurement,and Control,1985,18(1): 200-206.
[4]Chin C,Nayfeh A,Mook D.Dynamic and control of ship-mounted cranes[C]//Proceedings of the 39th Structures,Structural Dynamics,and Materials Conference Long Beach,California,1998.
[5]Masoud Z N,Nayfeh A H,Mook D T.Cargo pendulation reduction of ship-mounted cranes[J].Nonlinear Dynamics,2004,12(4): 299-311.
[6]Tanaka S,Kouno S,Automatic measurement and control of the attitude of crane lifters: lifter attitude measure and control[J].Control Engage Prictice,1998(6): 1099-1107.
[7]董明晓,郑康平,张明勤.桥式起重机消摆控制仿真研究[J].系统仿真学报,2005 (1): 13-16.
[8]高丙团,陈宏钧,张晓华.龙门吊车负载定位的一种非线性控制方法[C]//中国控制与决策学术年会论文集,2005: 196-202.
[9]贾智勇.船上回转式吊车的防摆控制研究[D].哈尔滨: 哈尔滨工业大学,2007.
Research on Active Pendulation Control of Davit for Working Boat Based on Adaptive Iterative Learning Control Method
GAO Yun-jian1,SHI Hong-yu2
(1.Military Agent's Room of Naval Armaments Department Stationed in Shanghai,Shanghai 201210,China;2.Harbin Engineering University,Harbin 150001,China)
The davit installed on the ship is mainly used for improving the security and efficiency of offshore operations during the process of folding and unfolding a working boat.Based on Lagrange equations,a dynamic model is derived for typical underactuated mechanical davit system.According to the actual movements of the ship,two-dimensional model of the system is described in detail to analyze the swing angle of the boat,which is changed with the movements of ship.Then,based on thisNOnlinear dynamic model,a closed-loop controller is designed to reduce swing angle and improve the working efficiency.Finally,the simulation results can verify the effectiveness of the control method.
davit; dynamic model; Lagrange equations; partial feedback linearization; adaptive iterative learning control
TV22
A
10.16443/j.cnki.31-1420.2015.03.011
高云剑(1973-),男,工程师,工学硕士,导航制导与控制专业。

