不同斜腔角驱动流的非结构网格研究
赵 楠,陈笑薇,丁 亮
(1.海军驻上海地区舰艇设计研究军事代表室,上海 201001; 2.中国船舶及海洋工程设计研究院,上海200011;3.上海船舶设备研究所,200031)
不同斜腔角驱动流的非结构网格研究
赵 楠1,陈笑薇2,丁 亮3
(1.海军驻上海地区舰艇设计研究军事代表室,上海 201001; 2.中国船舶及海洋工程设计研究院,上海200011;3.上海船舶设备研究所,200031)
在雷诺数100和1000两种情况下,使用非结构网格技术对15°~165°斜腔驱动流问题进行了数值模拟。首先与已有的文献结果进行了对比,当使用网格数为文献 1/7网格数时,模拟结果与文献符合的很好,表明非结构网格对于只能用非正交结构网格求解的问题有很大的优越性。然后对大斜角斜腔的驱动流场进行了预测。结果能为不同斜腔角的流场研究提供参考,并对工业类似结构的设计有一定的借鉴意义。
非结构网格;阵面推进法;SIMPLE算法;斜腔驱动流
0 引言
驱动流的数值研究在文献中很常见,常被用于标准解来检验数值算法的稳定性、可靠性和高效性。其特点是几何简单,但包含基本的物理流动特征,在角区有反向旋转的回流区。Burggraf[1]早在1966年就研究了方腔驱动流内的流场。Gupta等[2]于1981年使用半分析的方法给出了小雷诺数下尖角附近的驱动流与奇点问题,并与其他文献的数值解进行了比较。 Ghia[3]使用了涡流函数法以及多重网格加速技术,在(129×129)网格数下对雷诺数 Re=1000的方腔驱动流给出了数值解。该文后来成为方腔驱动流较早的基准解之一,被大量后续研究者作为对比基准。Botella等[4]采用Chebyshev谱方法,Tezduyar[5]采用有限元法也分别给出了雷诺数下100和1000时的方腔驱动流内部流场。Stortkuhl等[6]首先用分析渐进解的方法给出了角区附近的流动解,然后使用多重网格法给出数值解,并指出随着网格尺度的减小,数值解逐渐向渐进解靠近。Li等[7]使用高阶的紧致四阶有限差分格式,给出了雷诺数小于7500时的流场解。Tucker和Pan[8]没有局限于数值算法,而是利用切割单元方法给出了驱动流流场解。Bruneau等[9]对两维方腔驱动流进行了回顾并给出了Re=10000以内的基准解。相对方腔驱动流而言,由于斜腔驱动流内部网格划分的不正交对数值算法提出了新的要求,对斜腔流的研究较少。Peric等[10]为了弥补非正交网格数值解法的不足,使用了较密的(160×160)和(320×320)两种网格,分别给出了在斜腔角30º时Re=100和1000时的数值解,作者使用有限体积的SIMPLE算法求解结构网格内的N-S方程,并使用了多重网格加速技术。Oosterlee等[11]使用有限体积方法求解了一般曲线坐标下斜腔角30º和45º时定常不可压缩N-S方程问题,给出了斜腔流动的数值解。
大部分对于斜腔驱动流的研究主要集中在斜腔角30º和 45º,且使用的都是结构化网格,很少使用非结构化网格的。非结构网格主要用于处理复杂外形、减小生成复杂网格生成时间上。由于易于网格自适应和采用动网格技术,在复杂几何中得到广泛应用[12]。事实上,受到设备内部流动空间的限制,斜腔驱动流在工业上应用十分广泛,如斜船坞内流动,叶轮机械机匣处理的斜槽内流动以及轴承迷宫密封内的不稳定流动等。对于斜腔内流动问题的研究有助于了解这些复杂物理背景中的流场,对其内部的流场结构等情况加深认识,进而在结构设计阶段给予建议,优化产品或结构设计,减少流动损失。
本文在张楚华[13]研究基础上使用阵面推进法生成非结构网格,利用Laplacian算子和对角交换技术改善生成网格质量,对斜腔驱动流从斜腔角15º~165º范围进行了N-S方程求解,给出了内部详细流场,并与已有的标准解进行了比较。一方面验证网格生成以及流场计算程序的可靠性,考核非结构网格用于简单几何问题的精度,另一方面给出各种斜腔角时的数值解,为以后不同斜腔角的流场研究提供参考,并对工业类似结构的设计予以借鉴意义。
1 阵面推进法
阵面推进法(Advancing front method)是最常见的非结构网格生成方法之一[14-16],该方法的优点是不会引起物面穿透,边界附近网格质量高。缺点是生成效率低,对背景网格的依赖性较强。其基本生成方法如图1所示。首先输入边界离散点(如AB),形成初始阵面,然后根据背景非结构化网格上所提供的局部尺寸参数,依据式(1)计算。

式中:Sm是AB中点尺度;S1是新生成点C离A、B点的距离。在阵面左侧生成新的网格点(图1中C点),对该点及其某半径r范围内的点按式(2)、(3)进行筛选。

选取候选点序列(如Ni),最后根据交叉判断原则,剔除交叉点并选取最合适的点(图1中D点),形成新的三角形(如ABD), 最后修改阵面,使边界点的连接信息向流场内部推进,直至整个流动区域被三角形覆盖为止。

图1 阵面推进法示意图
使用上述算法生成的网格有时质量较差,会生成畸形网格,需要对其进行网格光顺和对角交换。如图2(a)所示,对角交换改变了网格的拓扑结构,实现了局部网格最小内角最大化的原则。而图2(b)的网格光顺则对网格单元的顶点几何位置使用式(4)改进。
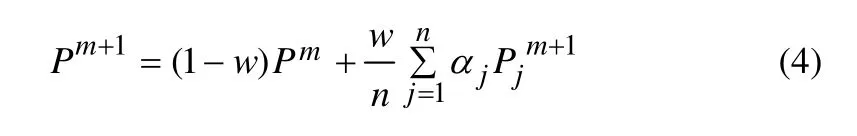
式中:Pj是待优化P节点的临近点坐标,目的是将网格点尽可能地移到临近网格点的中心。
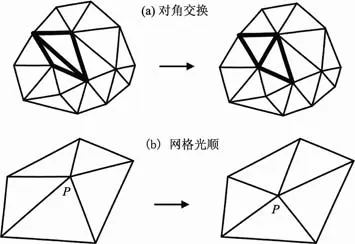
图2 网格优化技术
2 数值公式
非结构化网格方法不需要进行坐标转换,直接在原物理空间求解。在流动为定常不可压缩的假设下,平面笛卡尔坐标系中的N-S方程可写为通用形式:

式中:Φ为任一输运量;ΓΦ为广义扩散系数;为广义源项;将控制方程(5)写成积分形式:
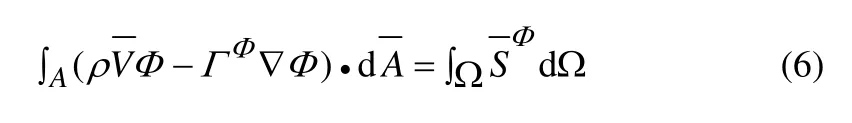
式中:ρ为密度;Ω为积分区域;A为Ω的边界。直接采用三角形单元为有限控制容积,所有的求解变量Φ位于三角形的几何中心,这样对任意三角形单元,方程(6)可以离散为:
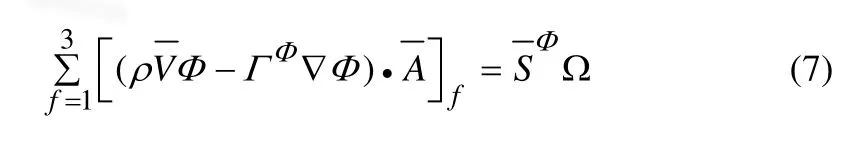
对方程(7)扩散项的离散要用到界面上的变量梯度,而对源项要用到中心点的梯度。界面上的梯度计算用图3(a)所示的b-c-d-a积分曲线,假定界面梯度值为沿着积分曲线的平均值,可得:


图3 梯度计算积分曲线
对于单元中心的梯度,采用高斯定理重构,选取积分区域V为三角形单元C,并设单元中心处的梯度值为单元梯度的平均值:

式中:f1为线性插值系数;ΔV为单元C的面积,当单元C为界面f的左单元时取正号,当单元C为界面f的右单元时取负号。
对于对流项中的界面变量值,使用二阶精度混合差分格式,当Peclet数的绝对值小于2时采用中心差分格式,大于2时采用二阶迎风格式:

3 流场求解
采用推广至非结构网格的同位网格Simple方法求解流场压力分布,其基本步骤为:
1)预估步,对于假定的压力分布P*,求解动量方程得到预估的速度U*、V*。
2)校正步,求解压力和速度的校正值,使得校正后的压力场和速度场同时满足连续方程和动量方程。
为防止压力场和速度场的失耦,将动量方程的压力梯度项采用中心差分离散,但界面流速采用Rhie和Chow[17]提出的界面流速“压力加权插值”式(11)计算。
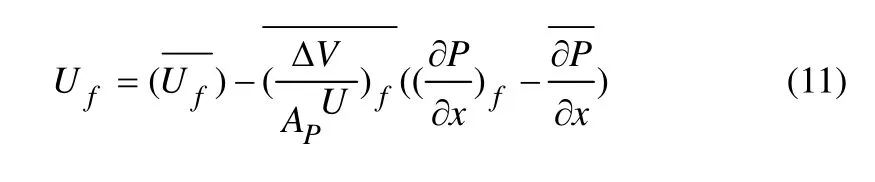
这样相邻点的压力通过离散系数以及质量流量影响速度和压力场,实现速度场和压力场的关联。将式(11)应用到非结构网格中,得到相应界面质量流表达式为:

4 物理模型
二维斜腔驱动流物理问题的示意图(见图4)。AB、BC、CD为三个静止固体壁面,而AD边之外的流体以恒定速度UL沿着水平方向运动。无量纲雷诺数定义为Re=(ρULL)/μ,(μ为摩擦系数)。在 Re为100和 1000两种情形使用阵面推进法生成非结构网格,对于斜腔角α从15º~165º进行了数值模拟,与已有文献的结果进行对比,并给出了更广范围斜腔角的内部流场特征量。
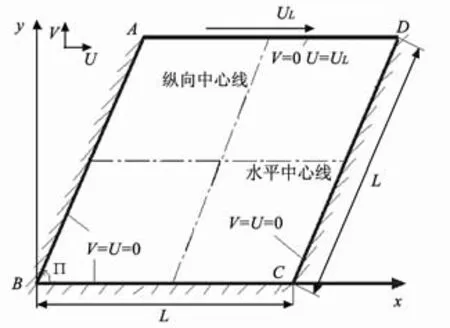
图4 斜腔驱动流物理模型
5 数值结果
为验证程序的正确性,首先将计算得到结果与文献[18]、[9]给出的斜腔算例结果做了对比,雷诺数1000时斜腔角α=30º、45º的流线对比结果如图5所示。

图5 Re=1000时斜腔角30º和45º流线对比
很明显,这两个斜腔角时斜腔内流动结构主要由两个大涡组成。本文计算得到的30º和45º两种情况下,两个大涡的分界线端点分别是(0.8,0.45)和(1.45,0.25),(0.65,0.65)和(1.35,0.35),这与文献[18]符合的很好,但本文计算还在左下尖角处分辨出更小的涡结构。
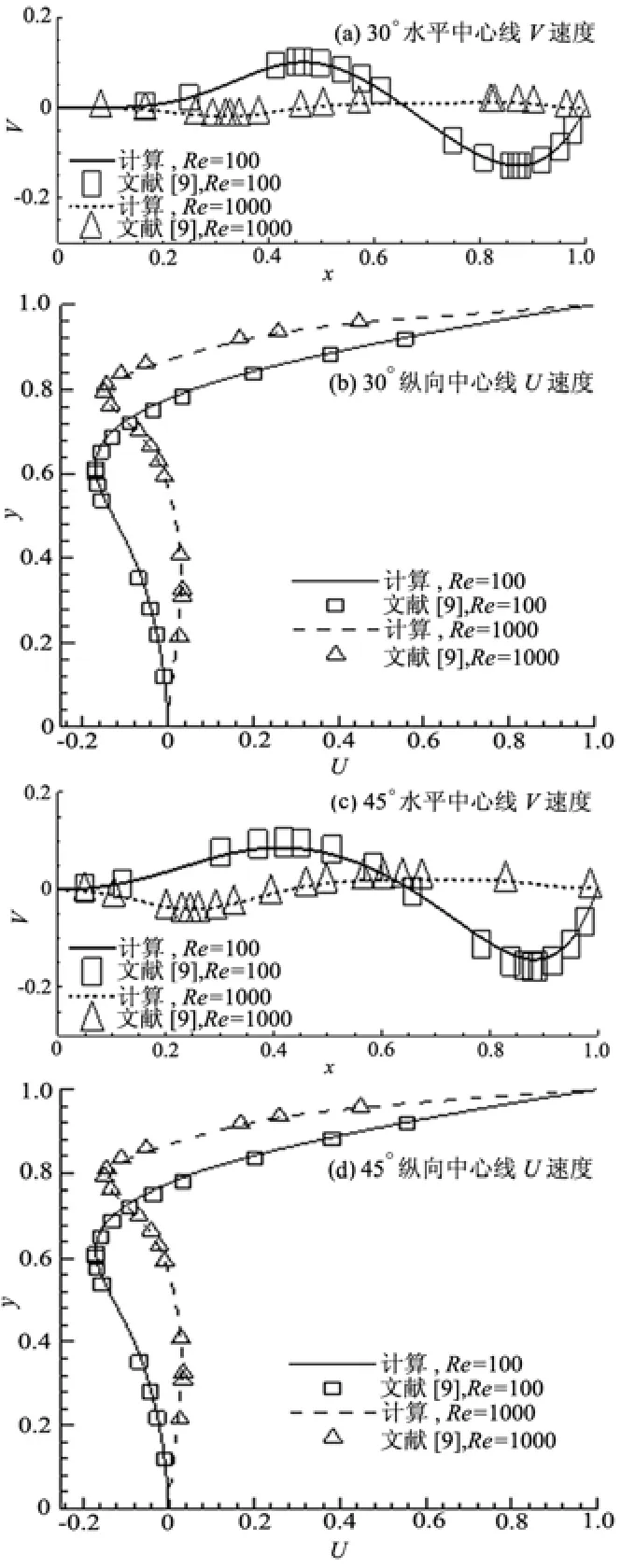
图6 不同斜角的中心线速度分布对比
文献[18]只给出了各物理量等值线的分布,没有给出定量的数据。为了在定量上比较,又与文献[9]中使用320×320的网格计算出的数值解结果做了对比。在Re分别是100和1000时,对30º斜腔和45º斜腔两种情形水平中心线的V速度和纵向中心线处的U速度值共8条曲线进行了对比,结果如图6所示。斜腔角45º时于x=0.404处达到V最大值0.082,x=0.879时达到V最小值-0.143。而在雷诺数为1000时,速度分布沿 x轴是先减小后增大再减小:斜腔角 30º时于x=0.31处达到V最小值-0.019,x=0.818时达到V最大值0.0174。斜腔角 45º时于x=0.253处达到V最小值-0.0398,x=0.6565时达到V最大值0.0212。速度的极值分布见表1。从图6(b)、(d)的纵向中心线处的速度分布看出,雷诺数1000时无论是斜角30º还是45º,U速度均在y=0.9左右处衰减为0,并继续减小,变为负值,到y=0.78处减小至负最小值;雷诺数100时U速度在y=0.75处衰减为0,并继续减小,变为负值,到y=0.6左右处减小至负最小值。分析比较不同斜腔角度的速度线,再次证明了斜腔角度的影响相对于雷诺数而言是比较小的。表 2中给出了纵向中心线处的极值分布点。此外,文献[9]中使用的是结构网格,本程序用的是非结构网格,总三角形单元数为16302个,相当于125×125的结构网格,其单元数是文献[9]的 1/7。比较结果证明,二者计算精度完全相当,亦表明非结构网格对于只能用非正交结构网格求解的问题有很大的优越性,使用较少的网格即可以得到较准确的结果。

表1 水平中心线V速度极值点

表2 纵向中心线U速度极值点
图6(a)、(c)分别是斜角30º和45º斜腔水平中心线处的速度V沿着x轴的分布,图6(b)、(d)是纵向中心线处的速度U沿着y轴的分布。实线─、虚线┈分别是雷诺数100和1000时的计算值,方形□和三角△分别是文献[9]中雷诺数100和1000时的值。比较图6(a)、(c)可以看出,不同的斜腔角度对速度大小有一定影响,但速度变化趋势较类似。雷诺数为100时,速度V沿着x方向先增大后减小再增大:斜腔角30º时于x=0.465处达到V最大值0.1,x=0.869时达到V最小值-0.128。
进一步来说,若考虑到右上角主涡旋中心位置是流场中的主要特征量,与文献[1,3,19-24]给出的90º方腔主涡旋坐标进行了比较,比较结果如表 3所示。文献[24]给出了雷诺数100时的实验结果,本文计算得到的雷诺数100时的结果与其符合的很好。
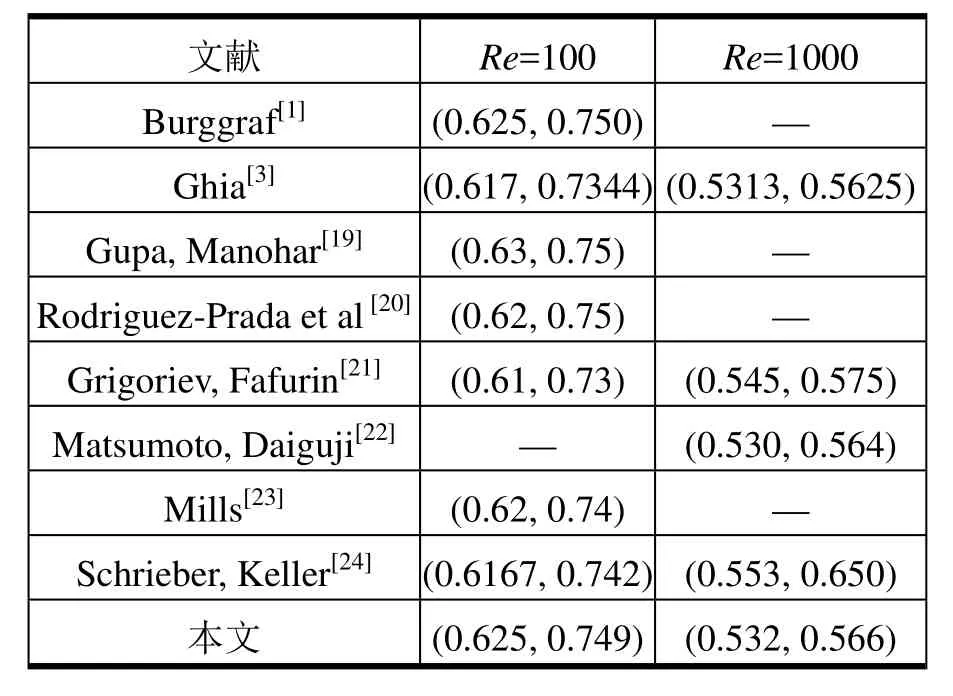
表3 主涡旋中心坐标比较
上文多角度的将本文计算结果与文献中已有的结果进行了对比,充分证明了该计算结果的可信性,亦表明非结构网格在对于只能用非正交结构网格问题时有足够的精度。图7、8给出了雷诺数100和1000时计算得到的斜腔角15º至165º时内部流场的流线分布。

图7 Re=100时15°~165°斜角的流线

图8 Re=1000时15°~165°斜角的流线
表4给出了各个斜腔角时主涡旋的位置坐标。比较两种雷诺数的主涡旋位置坐标发现,随着雷诺数的增加,在水平方向上,当斜腔角位于 15°~60°时,主涡旋位置向右侧偏移,而在75°~120°时,又向左侧偏移,在135°~165°时再次向左侧偏移;在垂直方向上,随着雷诺数的增加,当斜腔角位于 15°~45°时,主涡旋位置向上部偏移,而在60°~165°时,主涡旋位置向下部移动。两种雷诺数下,主涡旋的 x坐标都在斜腔角 30°时达到最大值,并随着斜角的增加而变小。在Re=100时,主涡旋的y坐标在90°时取得极大值,而Re=1000时主涡旋的y坐标在60°取得最大值。
比较图7、8的流线分布可以看出,随着雷诺数的增加,流场特征变化最大的集中在斜腔角 30°~60°,在 Re=100时流场的涡结构主要由一个主涡构成,而Re=1000时是明显的两个大涡结构。在斜腔角处于120°~150°时,两种流场主要差别集中在AB边侧。在Re=1000情况下的AB边侧能捕捉到明显的涡结构,而Re=100时 AB侧是较平滑的流线。对于斜腔角 15°和165°时,除了主涡位置外,两种雷诺数下的流线并没有显示出明显的性质区别。

表4 不同斜腔角的主涡旋中心位置坐标
6 结论
本文利用非结构网格技术,对雷诺数100和1000时 15°~165°范围斜腔角的驱动流问题进行了数值模拟,得到的结论如下:
1)首次采用非结构网格方法对不同斜角驱动流问题进行了研究。
2)本文计算结果与已有文献结果比较表明,非结构网格对于那些只能用非正交结构网格求解的问题有很大的优越性,使用较少的网格即可得到可靠的结果。
3)斜腔驱动流中心线的速度受到雷诺数的影响比较大,速度分布会因雷诺数不同呈现性质上的变化;相对而言,斜腔角度只对速度值大小有一定影响,但不会影响速度分布趋势。
[1]Burggraf O R.Analytical and numerical studies of the structure of steady separated flows[J].J.of Fluid Mech.,1966,24: 113-151.
[2]Gupta M M,Manohar R P,NOble B.Nature of viscous flows near sharp corners[J].Comput.Fluids 1981,9: 379-388.
[3]Ghia U,Ghia K N,Shin C T.High-Re solutions for incompressible flow using Navier-Stokes equations and a multigrid method[J].J.Comp.Phys,1982,48(3):387-411.
[4]Botella O,Peyret R.Benchmark spectral results on the lid-driven cavity flow[J].Comput.Fluids,1998,27(4): 421-433.
[5]Tezduyar T E.Stabilized finite element formulations for incompressible flow computations[J].Adv.Appl.Mech.,1992,28: 1-44.
[6]Stortkuhl T,Zenger C,Zimmer S.An asymptotic solution for the singularity at the angular point of the lid driven cavity[J].Int.J.Numer.Meth.Heat &Fluid Flow,1994,4,47-59.
[7]Li M,Tang T,Fornberg B.A compact fourth-order finite difference scheme for the steady incompressible Navier-Stokes equations[J].Int.J.Numer.Meth.Fluids,1995,20,1137-1151.
[8]Tucker P G,Pan Z.A cartesian cut cell method for incompressible viscous flow[J].Appl.Math.Mod.,2000,24: 591-606.
[9]Bruneau C H,Saad M.The 2D lid-driven cavity problem revisited [J].Comp.Fluids,2005,35(3):326-348.
[10]Demirdzic,Lilek Z,Peric M.Fluid flow and heat transfer test problems forNOn orthogonal grids:benchmark solutions[J].Int.J.Numer.Methods Fluids,1992,15(3): 329-354.
[11]Oosterlee C W,Wesseling P,Segal A.Benchmark solutions for the incompressible navier-stokes equations in general coordinate on staggered grids[J].Int.J.Numer.Methods Fluids,1993,17:301-321.
[12]Mavriplis D J.Unstructured grid technique[J].Annual Review of Fluid Mechanics,1997,29: 473-514.
[13]张楚华.三维湍流流动的非结构化网格数值解法及其在离心风机中的应用研究[D].西安: 西安交通大学,1998.
[14]Löhner R,Parikh P.Three-dimensional grid generation by the advancing front method[J].International Journal for Numerical Methods in Fluids,1988,8:1135-1149.
[15]Lohner R.Progress in grid generation via the advancing front technique[J].Engineering with Computers,1996,12:186-210.
[16]Thompson J F,Soni B K,Weatherill N P,et al.Handbook of grid generation[M].America: CRC Press,1998.
[17]Rhie C M,Chow W l.A numerical study of the turbulent flow past an isolated airfoil with trailing edge separation[J].AIAA J,1983,21: 1525-1534.
[18]Louaked M,Hanich L,Nguyen K D.An efficient finite difference technique for computing incompressible viscous flows[J].Int.J.Numer.Methods Fluids,1997,25(9): 1057-1082.
[19]Gupta M M,Manohar R P.Boundary approximations and accuracy in viscous flow computations[J].Journal of Computational Physics,1979,31: 265.
[20]Rodriguez-Prada H A,Pironti F F,Saez A E.Fundamental solutions of the streamfunction vorticity formulation of the Navier–Stokes equations[J].International Journal for Numerical Methods in Fluids,1990,10: 1-12.
[21]Grigoriev M M,Fafurin A V.A boundary element method for steady viscous fluid flow using penalty function formulation[J].International Journal for Numerical Methods in Fluids,1997,25: 907-929.
[22]Matumoto Y,Daiguji H.Convective-difference scheme using a general curvilinear coordinate grid for incompressible viscous flow problems[J].JSME International Journal Series II,1992,35: 4-9.
[23]Mills R D.Experimental investigation on cavity flows[J].Jourmal of Radar and Aeronautics 1965,69: 714.
[24]Schreiber R,Keller H B.Driven cavity flows by efficient numerical techniques[J].J.of Comp.Phys.,1983,49(2):310-333.
Study on Unstructured Grids of Inclined Cavity Driven Flow with Different Angles
ZHAO Nan1,CHEN Xiao-wei1,DING Liang3
(1.Navy Representative office at Warship Design and Research in Shanghai,Shanghai 201001,China; 2.Marine Design & Research Institute of China,Shanghai 201011,China; 3.Shanghai Marine Equipment Institute,Shanghai 200031,China)
The inclined cavity driven flow with inclined cavity angles of 15°-165° is numerically simulated by using unstructured grid method at Reynolds number of 100 and 1000.First,its results are compared with the existing literature results.When using the grid number is 1/7 grid number of reference literature,the simulation results are in good agreement with results of literature.It indicates that the unstructured grid has great advantage for problems that can only be solved withNOn-orthogonal structured grids.Then,the driven flow filed of inclined cavity with large angle is predicted.The results can provide a reference for flow field study of different inclined cavity angles and has the certain significance for the design of similar industrial structures.
unstructured grid; advancing front method; SIMPLE algorithm; inclined cavity driven flow
V211
A
10.16443/j.cnki.31-1420.2015.03.009
赵楠,男,工程师。轮机工程专业。

