环境与结构因素对输电线舞动的影响

高仕赵，李欣业

（1.鲁东大学土木工程学院，山东烟台264025；2.河北工业大学机械工程学院，天津300130）

环境与结构因素对输电线舞动的影响

高仕赵1，李欣业2

（1.鲁东大学土木工程学院，山东烟台264025；2.河北工业大学机械工程学院，天津300130）

为了确定环境与结构因素对输电线舞动的影响，将输电线舞动的流固耦合问题简化为在气动力作用下的瞬态动力学问题.首先，根据悬索链理论进行静态找型，确定输电线的初始状态，并利用Hartog Den的垂直舞动机理和O.Nigol的扭振机理确定输电线所受到的气动力.其次，应用ANSYS的APDL语言编写有限元批处理程序，建立了两自由度输电线舞动的有限元模型，并依据已有的数据对此模型进行校验.最后，应用所建立的模型分析了风速、空气密度、阻尼比以及初始张力等参数对输电线舞动的影响.结果表明，舞动振幅随风速与空气密度的增大而增大，随阻尼比以及初始张力的增大而减小.

输电线；舞动；有限元模型；垂直舞动机理；扭转舞动机理

自二十世纪中叶以来工业化进程不断加深，与此同时带来了用电需求的显著增加.随着我国工业化现代化进程的不断推进，用电需求表现为以下几个特点：需求量增加、输电导线的容量增大、供电地点分散、输电距离增长，因此导致了远距离、大跨度输电线路被广泛应用.但是在一些地区，因为地势和气候等因素的影响，在恒速气流中，覆冰输电线产生的空气动力将引起输电线的舞动.在这种情况下，舞动引起的振幅可能导致相邻的输电线之间碰撞，发生跳闸现象.另外，长时间大幅振动会导致绝缘子、金具和支撑塔产生严重的损坏，严重时可能还会导致倒塔和断线等事故发生［1］.

由于引起输电线舞动的环境和几何因素非常复杂，迄今为止世界上公认的输电线舞动机理为邓哈托（Hartog Den）的垂直舞动机理［2］和尼戈尔（O. Nigol）的扭振机理［3-4］.垂直舞动机理是由邓哈托首先提出，后来又由C.O.Harris和J.J.Ratkowski等人补充完整.邓哈托的垂直舞动机理认为当静止的输电线受到水平恒速风的作用时会产生小幅的上下振动，导线就必然有一个垂直方向的速度，根据速度合成原理可知导线就相当于受到一个与水平方向成一定夹角的风速的作用，也就是说导线受到一个与水平方向成一定角度的气动力的作用.在舞动振幅较小时，风速输入到输电线系统的能量大于系统阻尼消耗掉的能量，导线舞动振幅就会增加.当舞动振幅达到一定程度时，输电线系统的阻尼消耗掉的能量等于风速输入到输电线系统的能量，舞动达到平衡.尼戈尔提出的扭振机理认为，由于覆冰导线的重心和原有导线的重心不重合以及气动力的作用中心和输电线的中心不重合产生了扭矩，加之输电线也有一定的扭转刚度，这样随着攻角的变化气动力也随之变化，便产生了扭转振动，又由扭转振动产生垂直舞动.

文中拟以邓哈托的垂直舞动机理和尼戈尔扭振机理为依据，并融入悬索链理论建立输电线舞动的有限元模型；然后用已有数据对此模型进行校验；最后应用校验后的有限元模型对输电线舞动的各种影响因素进行仿真分析，得出各影响因素与舞动之间的关系曲线.

1　输电线静态找型理论

从广义上说输电线属于柔索的一种，在研究输电线找型问题时，可以将输电线按柔索进行处理.由于柔索本身没有固定的形状，在给定的边界条件下，所施加的预张力、自重荷载以及覆冰荷载需通过调节柔索的形状来达到平衡.文中根据悬索链理论并采用数值迭代计算方法来实现输电线找型.

为简化输电线静态找型计算，需作几点基本假设：①输电线既不抗压，也不抗弯；②输电线材料的应力和应变符合线性关系；③各个输电线单元所受的荷载沿长度方向均匀分布；④输电线舞动属于大位移、小应变问题［5-7］.图1为输电线及其微元体模型.

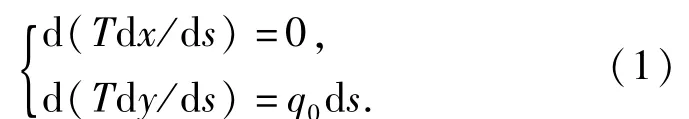
由式（1）可知T d x/d s=T cosθ=H，即拉力的水平分量处处相等.则变形曲线为

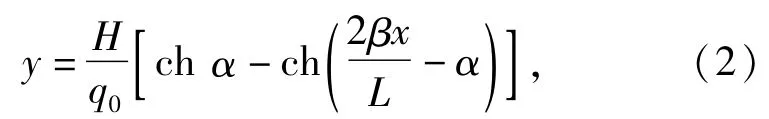
中垂度为

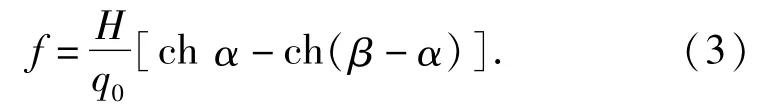
最大张力为

2　输电线舞动理论模型

覆冰导线在受风激励作用下，其截面的质量中心与旋转中心不再重合，因此，在风激励下，它所产生的横向振动与扭转振动将会存在两方面的耦合［1，7-8］：①由于质量偏心产生的惯性耦合；②由于攻角变化产生的空气动力耦合.

两自由度舞动模型包括垂直振动和扭转振动，其既包括邓哈托的垂直舞动机理，又包括了尼戈尔的扭振机理，理论模型更接近于实际情况.图2为输电线舞动的二自由度驰振模型.

图2中，横向振动只考虑了垂直方向的振动，而不考虑水平方向的振动.图2a所示的振动系统可使用图2b所示的定坐标系YOZ和动坐标系Yaa Za来描述，其中，动坐标系Yaa Za的坐标原点设在物体的转动中心a，其坐标为y和x，动坐标系绕a点的转动用θt来描述.图中：ky为拉压弹簧，表示系统在垂直方向的刚度；kt为扭转弹簧，表示系统的扭转刚度；G为物体的重心，它与转动中心a之间的距离e为偏心距.

设物体上的任一点s，在动坐标系的坐标为（ya，za），动坐标系的转角为θt，则该点在定坐标系的坐标为

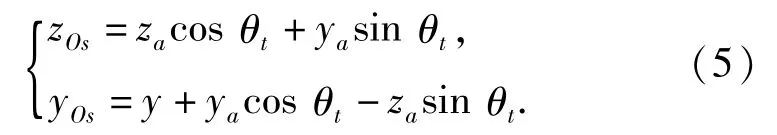
当θt的值足够小时，可近似地取为

相应的振动速度为

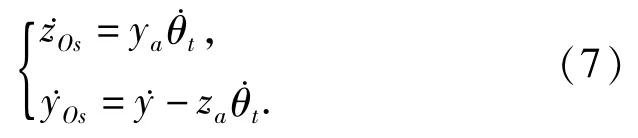
覆冰导线的动能为

其中：

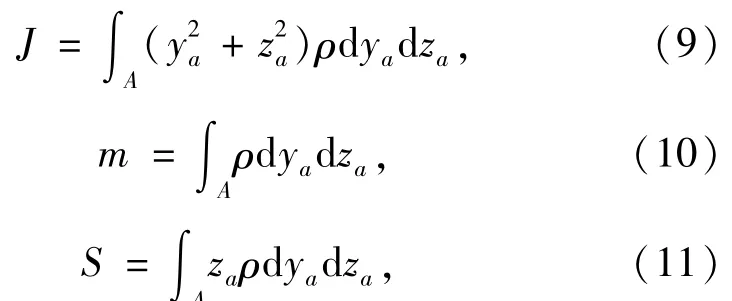
式中：ρ为覆冰导线单位面积的密度；J为转动惯量；S为偏心量，为覆冰导线质量与偏心距的乘积，即S=me≈mir，mi为覆冰质量，r为导线半径.

覆冰导线的势能为

拉格朗日方程为

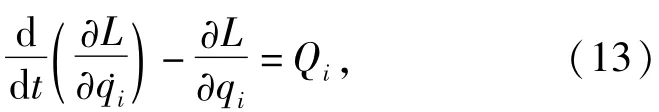
式中：L=T-V；Qi可由虚位移原理求得.即有

式中：Qy为y轴方向的气动力与阻尼力之和；Qt为扭转方向的气动力与阻尼力之和；Fy为y向气动力；M为扭转方向的气动力；Cy为横向振动阻尼系数，Cy= 2mζyωy；Ct为扭转振动组尼系数，Ct=2Jζtωt.

将式（8），（12），（15）-（16）代入式（13）得

其中Fy和M可表示为如下形式：

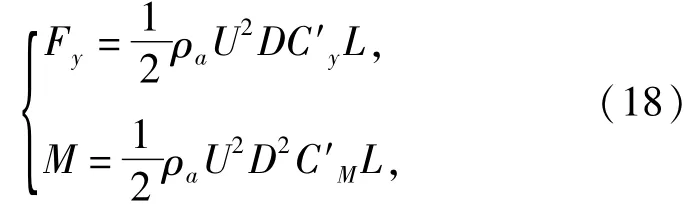
式中：ρa为气流密度；U为气流速度；D为迎风尺寸；C′y和C′M分别为y向和扭转方向的气动系数.

3　输电线舞动仿真模型验证

输电线舞动属于典型的流固耦合问题，但输电线跨度长，舞动的空间范围大，因此，流固耦合问题的计算成本非常高昂.但由于导线的截面面积相较于它的舞动刨面要小的多，因此其对空气流动的影响非常有限，可以忽略不计［9-11］.

系统参数如下：风速，10 m·s-1；导线直径，28.142 mm；单位长度导线质量，1.798 kg；导线长度，244 m；空气密度，1.29 kg·m-3；扭转刚度，432 N·m-2·rad-1；阻尼比，0.182；弹性模量，100 940 MPa；初始覆冰角度，30°；初始张力，26 kN.

文中根据这一假设条件将输电线舞动的流固耦合问题简化为输电线在气动力作用下的瞬态动力学问题，并根据ANSYS的APDL语言编写了有限元模型的仿真程序［8，11-12］.图3为此程序的流程图.

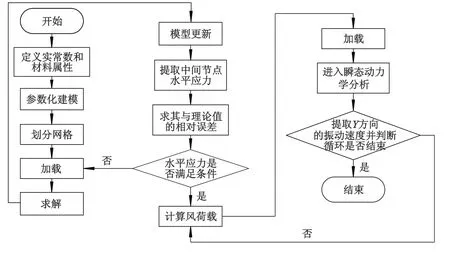
图3　程序流程图

文中采用参考文献［13］所提供的系统参数值.根据有限元方法计算出来的垂直结果如图4-7所示.其结果值与文献［13］的垂直相对误差为25.4%，扭转相对误差为18.2%.通过这一计算结果和已有文献的比对可知：本程序在计算两自由度模型上具有一定的精度.

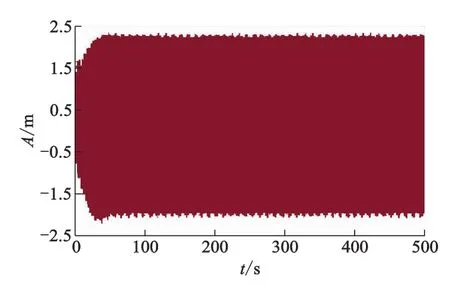
图4　y向的时间历程

图5　图4的局部放大图

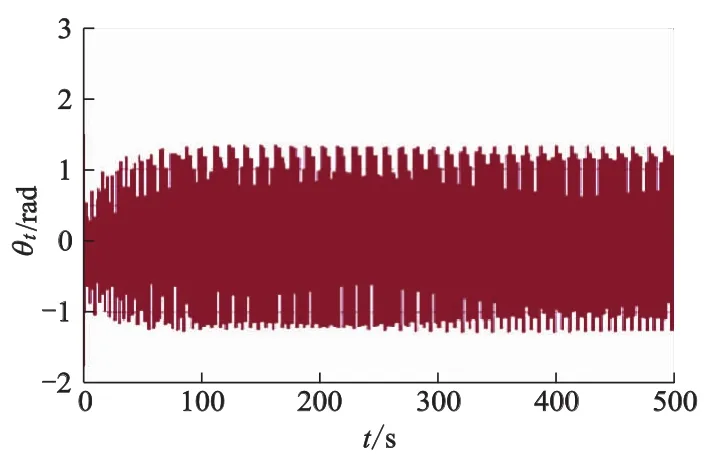
图6　扭转方向的时间历程

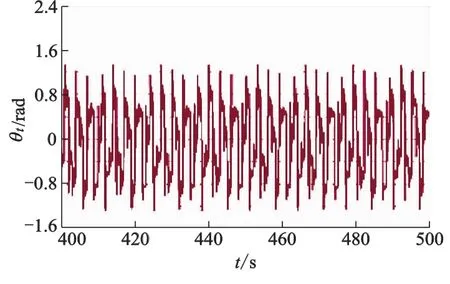
图7　图6的局部放大图

4　输电线舞动的影响因素分析

影响输电线舞动的环境与结构因素主要包括风速、空气密度、阻尼比以及初始张力，文中应用前面验证后的有限元模型对上述影响因素进行系统分析.

4.1风速对舞动的影响

图8为风速对舞动的影响曲线.

图8　风速对舞动振幅和扭转角度的影响

由图8可见：舞动振幅和扭转角度随风速增加而增加，在风速达到8 m·s-1后，舞动振幅和扭转角度迅速增加.风速由8 m·s-1增加到14 m·s-1，风速增加了75%，而舞动振幅由1.02 m增加到4.53 m，振幅增加了344%.而扭转角度在风速由8 m·s-1增加到10 m·s-1时，风速增加了25%，扭转角度增加了100%.风速对舞动的影响是非常显著的，这也就是输电线舞动多发生在风口收窄的山口地区的原因.因此在这些地区架设高压输电线路时，一定要注意输电线的舞动问题.

4.2空气密度对舞动的影响

由于高压输电线路一般架设在空旷的野外，因此一年四季的温度变化比较明显，由于热胀冷缩效应，在冬季时空气的密度相较于夏季要高一些.图9反映了舞动振幅和扭转角度随空气密度的变化情况.

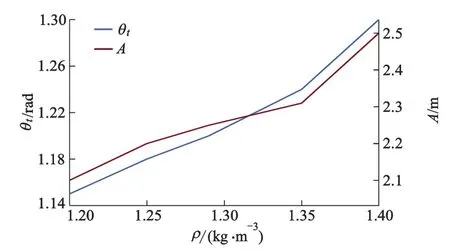
图9　空气密度对舞动振幅和扭转角度的影响

从图9可见，舞动振幅和扭转角度随空气密度的增加而增加.但其变化幅度相较于风速对输电线舞动的影响要小得多.当温度降低或是空气里夹杂着其他物质（如小雨滴或者是小冰凌等）增加了空气的密度时，都有可能成为引起输电线舞动的原因.

4.3阻尼比对舞动的影响

图10为阻尼比对舞动的影响曲线.

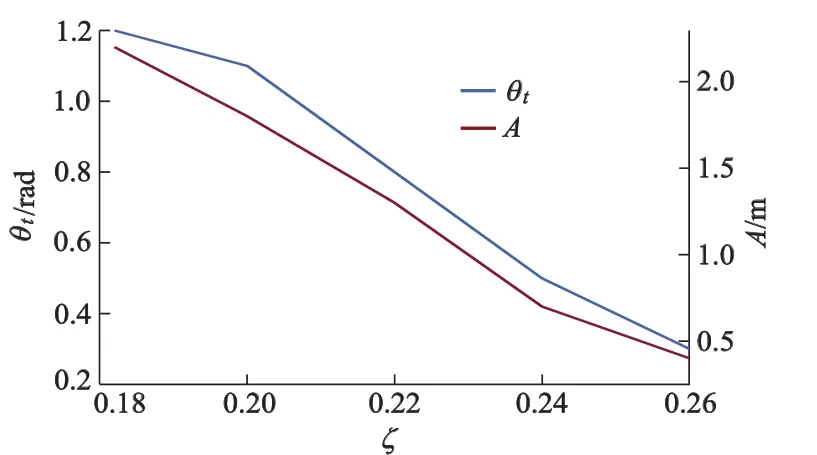
图10　阻尼比对舞动振幅和扭转角度的影响

由图10可见输电线舞动的振幅和扭转角度随阻尼比的增大而降低.阻尼比由0.182增加到0.260，增加了43%，舞动振幅由2.25 m降低到0.45 m，降低了80%，舞动扭转角度由1.20 rad降低到0.32 rad，降低了73%.可以得出阻尼比的增加对舞动振幅和扭转角度的抑制作用是很明显的.这主要是因为当输电线舞动的输入能量一定时，随着阻尼比的增加，消耗输电线舞动的能量也随之迅速增加.因此输电线防舞的关键是消耗舞动的能量.

4.4初始张力对舞动的影响

图11为初始张力对舞动的影响曲线.

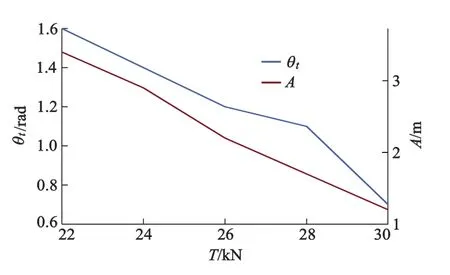
图11　初始张力对舞动振幅和扭转角度的影响

由图11可知输电线舞动振幅和扭转角度随初始张力的增大而降低.初始张力由22 kN增加到30 kN，增加了36%，舞动振幅由3.72 m降低到1.24 m，降低了67%，扭转角度由1.49 rad降低到0.68 rad，降低了54%.由此可得输电初始张力对舞动振幅和扭转角度的影响是非常明显的.这主要是因为初始张力的增加相当于增大了导线的刚度，因此可以通过增加初始张力，来降低舞动的振幅和扭转角度.

5　结 论

输电线舞动的影响因素主要包括风速、空气密度、阻尼比以及初始张力.前两个环境因素对舞动起加强作用，后两个结构因素对舞动起抑制作用.因此在设计输电线路时，收集拟建线路地区的环境因素是很重要的.另外，通过文中的仿真分析可知增加输电线初始张力与增加阻尼相比，其抑制舞动的效果同样显著，因此在条件容许的情况下，可以适当增加初始张力来提高输电线的舞动“门槛”，进而达到抑制输电线舞动的效果.

（References）

［1］ 郭应龙，恽俐丽，鲍务均，等.输电导线舞动研究［J］.武汉水利电力大学学报，1995，28（5）：506-509. Guo Yinglong，Yun Lili，BaoWujun，etal.A study on the galloping of overhead transmission line［J］.Journal ofWuhan University of Hydraulic and Electric Engineering，1995，28（5）：506-509.（in Chinese）

［2］ Yan Zhitao，Savory Eric，Li Zhengliang，et al.Galloping of iced quad-conductors bundles based on curved beam theory［J］.Journal of Sound and Vibration，2014，333（6）：1657-1670.

［3］ Yan Zhitao，Li Zhengliang，Savory Eric，et al.Galloping of a single iced conductor based on curved-beam theory［J］.Journal ofWind Engineering and Industrial Aerodynamics，2013，123（1）：77-87.

［4］ 陈常松，陈政清，颜东煌.悬索桥主缆初始位形的悬链线方程精细迭代分析法［J］.工程力学，2006，23（8）：62-68. Chen Changsong，Chen Zhengqing，Yan Donghuang. Accurate iterationmethod to calculate the initial states of main cables of suspension bridges［J］.Engineering Mechanics，2006，23（8）：62-68.（in Chinese）

［5］ 聂建国，陈必磊，肖建春.悬链线索单元算法的改进［J］.力学与实践，2003，25（4）：28-32. Nie Jianguo，Chen Bilei，Xiao Jianchun.An improved algorithm for catenary cable element［J］.Mechanics in Engineering，2003，25（4）：28-32.（in Chinese）

［6］ 李欣业，张振民，张华彪，等.Duffing-van der Pol振子的时滞反馈控制研究［J］.振动与冲击，2010，29（10）：118-121. Li Xinye，Zhang Zhenmin，Zhang Huabiao，et al. Feedback control with time delay on Duffing-van der Pol oscillators［J］.Journal of Vibration and Shock，2010，29（10）：118-121.（in Chinese）

［7］ Desai Y M，Yu P，Popplewell N，et al.Finite element modelling of transmission line galloping［J］.Computersand Structures，1995，57（3）：407-420.

［8］ Yan Zhimiao，Yan Zhitao，Li Zhengliang，et al.Nonlinear galloping of internally resonant iced transmission lines considering eccentricity［J］.Journal of Sound and Vibration，2012，331（15）：3599-3616.

［9］ 霍 涛，晏致涛，李正良，等.考虑弹性边界条件曲梁模型的覆冰输电线舞动［J］.振动与冲击，2013，32（21）：85-91. Huo Tao，Yan Zhitao，Li Zhengliang，et al.A curvedbeam model considering elastic boundary conditions for iced transmission line galloping［J］.Journal of Vibration and Shock，2013，32（21）：85-91.（in Chinese）

［10］ 李欣业，张华彪，侯书军，等.覆冰输电导线舞动的仿真分析［J］.振动工程学报，2010，23（1）：76-85. Li Xinye，Zhang Huabiao，Hou Shujun，etal.Theoretical and numerical analysis of galloping of iced power transmission lines［J］.Journal of Vibration Engineering，2010，23（1）：76-85.（in Chinese）

［11］ 左言言，常庆斌，耿 烽，等.轨道高低不平顺激励下的车体振动仿真［J］.江苏大学学报：自然科学版，2011，32（6）：647-651. Zuo Yanyan，Chang Qingbin，Geng Feng，et al.Simulation of vehicle vibration with excitation of rail height irregularity［J］.Journal of Jiangsu University：Natural Science Edition，2011，32（6）：647-651.（in Chinese）

［12］ 晏致涛，黄静文，李正良.基于结点6自由度的分裂导线有限元模型［J］.工程力学，2012，29（8）：325-332. Yan Zhitao，Huang Jingwen，Li Zhengliang.Finite elementmodel of bundle lines based on 6-DOF node［J］. Engineering Mechanics，2012，29（8）：325-332.（in Chinese）

［13］ Byun Gi Sig，Robert I Egbert.Two-degree-of-freedom analysis of power line galloping by describing function methods［J］.Electric Power Systems Research，1991，21（3）：187-193.

（责任编辑 梁家峰）

Influence of environmental and structural factors on transm ission line galloPing

Gao Shizhao1，Li Xinye2
（1.School of Civil Engineering，Ludong University，Yantai，Shandong 264025，China；2.School of Mechanical Engineering，Hebei University of Technology，Tianjin 300130，China）

To ascertain the influence of environmental and structural factors on the transmission line galloping，the transmission line dancing fluid-solid coupling problem was simplified to transient dynamics problem in aerodynamic effect.The suspension cable theory was used to determine the initial state of transmission line.The transmission line aerodynamic forceswere confirmed by Den.Hartog′s vertical gallopingmechanism and O.Nigol′s torsional galloping mechanism.The finite elementmodel（FEM）of transmission line dancing with two degrees of freedom was established based on APDL languages of ANSYSFEM，and the existing data were verified by the proposed model.The influences ofwind speed，air density，damping ratio and initial tension on power transmission line galloping were analyzed by the proposed model.The results show that the galloping amplitude is increased with the increasing ofwind speed and air density，and galloping amplitude is decreased with the increasing of damping ratio and initial tension.

transmission line；galloping；finite elementmethod；vertical gallopingmechanism；torsional gallopingmechanism

TU352；TU852

A

1671-7775（2015）04-0452-06

高仕赵，李欣业.环境与结构因素对输电线舞动的影响［J］.江苏大学学报：自然科学版，2015，36（4）：452-457.

10.3969/j.issn.1671-7775.2015.04.014

2015-03-08

国家自然科学基金资助项目（10872063）；山东省博士基金资助项目（BS2014SF016）；“泰山学者海外特聘专家”人才项目；鲁东大学博士启动基金资助项目（LY2014026）

高仕赵（1983—），男，天津蓟县人，博士，讲师（wooden20030044@126.com），主要从事输电线舞动研究.李欣业（1966—），男，河北唐山人，教授（xinyeli@eyou.com），主要从事非线性振动研究.