模体发现问题中OOPS模型的EM算法

黄影

摘 要 生物序列模体发现是从生物序列集合找出具有特定功能子序列的问题，它是生物信息学中最重要问题之一。OOPS模型是一种简单常用的模体发现的序列模型，它表示每条序列中有一个模体出现。本文提出了一种适用于OOPS序列模型的EM算法，用于查找每条序列中所出现的模体。实验结果表示，所提出的算法的时间性能和识别准确率均好于经典的Project算法。

关键词 模体发现 生物序列 EM算法

中图分类号：TP181 文献标识码：A DOI：10.16400/j.cnki.kjdkx.2015.08.010

EM Algorithm of OOPS Model in Motif Discovery Problem

HUANG Ying

（School of Information Engineering， Xi'an University， Xi'an， Shaanxi 710065）

Abstract Biological sequence motif discovery from biological sequence set to find out having a problem specific functional sub-sequence， it is one of the most important issues in bioinformatics. OOPS model series model is a simple common motif finding， which represents each sequence has a motif appears. This paper presents a suitable OOPS series model EM algorithm， for finding that appears in each sequence motif. The results indicated that the time performance of the algorithm and the recognition accuracy rate of the proposed algorithm is better than the classical Project.

Key words motif discovery; biological sequence; EM algorithm

1背景

EM（expectation-maximization）算法是Dempster， Laird和Rubin（DLR）三个人在1977年正式提出的。主要是用于在不完全数据的情况下计算最大似然估计。在EM算法正式提出以来，人们对EM算法的性质有更加深入的研究;并且在此基础上，提出了很多改进的算法，在数理统计，数据挖掘，机器学习以及模式识别等领域有广泛的应用。

生物序列模体（motif）发现问题是从一个从相关生物序列集合找出具有某种特定功能的子序列的问题，它是生物信息学中最重要问题之一，也是最基本问题之一。针对motif在每条序列中出现或不出现或者出现多次，有三种对应的模型，即：若每条序列中有且仅有一个motif出现，则被称为OOPS模型，这是最简单的模型;若每条序列中至多有一个motif出现，则被称为ZOOPS模型;若每条序列允许多个motif出现或者没有motif出现，则被称为TCM模型，这是最复杂的模型。

本文实现基于最简单的OOPS模型实现EM算法，来查找每条序列中所出现的motif。

2模体发现的EM算法

在最大化似然的问题中，给定被称为数据参数似然值的函数（ ; ），或者就称为似然函数：

（∣ ） = （∣ ） = （ ; ）

我们的目标就是找到使最大的 值，即

* =   （ ; ）

EM算法的核心思想就是根据已有的数据来递归估计似然函数。

所有的EM算法都由两个主要的步骤组成：

E-step

M-step

在E-step中，对于未知的潜在变量，使用当前参数的估计值和当前的观察。在M-step中，重新计算出来一个新的参数的估计值。在每次迭代中，似然值都会增加，因此该过程总会达到一个渐近最大值;但EM可能陷入一个局部最优。通过交替使用这两个步骤，EM算法逐步改进模型的参数，使参数和训练样本的似然概率逐渐增大，最后终止于一个极大点。

直观地理解EM算法，它也可被看作为一个逐次逼近算法：事先并不知道模型的参数，可以随机的选择一套参数或者事先粗略地给定某个初始参数，确定出对应于这组参数的最可能的状态，计算每个训练样本的可能结果的概率，在当前的状态下再由样本对参数修正，重新估计参数，并在新的参数下重新确定模型的状态，这样，通过多次的迭代，循环直至某个收敛条件满足为止，就可以使得模型的参数逐渐逼近真实参数。

EM算法的主要目的是提供一个简单的迭代算法计算后验密度函数，它的最大优点是简单和稳定，但容易陷入局部最优。

如果给定一组已比对好的序列集，可以直接构造一个表征motif的profile矩阵，即PWM;图1是一个例子。

但对于未比对的序列，我们怎么构造profile矩阵？因为在通常情况下，我们并不知道motif是什么，这时我们就可以使用EM算法。

使用概率矩阵 = 表示motif概率，这里表示列的字符所出现的概率。用概率 = 来表示背景（即，序列中motif之外的部分）概率，用表示背景中的字符的出现概率。并定义矩阵，其元素表示motif出现在序列的位置的概率。例如，在图2中，给定长度为6的3条DNA序列，这里motif的长度W=3，其对应的、和Z：

图1 给定一组已比对好的序列集，直接构造表征motif的profile矩阵

图2 给定长度为6的3条DNA序列，motif的长度W=3，对应的、和

整个EM算法的框架如下：

EM algorithm

Given： length parameter W， training set of sequences

set initial values for P

do    re-estimate Z from P           （E-step）

re-estimate P from Z           （M-step）

until change in P <

Return： P， Z

在E-step中， 由计算的估计即motif出现的最可能位置;在M-step中，由重新计算的估计即一个新的motif的PWM。

假定给定条长度为的序列： = （， ，…，）， = 1， …，，我们找出长度为的motif。则该序列在位置j出现motif的概率为：

在E-step：由计算

在E-step的第次迭代中，由下式计算获得：

= （ = 1∣ ， ， ）

=

假定motif等可能的出现在序列的任意位置，则上式可化简为：

=

在M-step：由计算

对于motif，对任意的，有

=

这里 =  。

对于背景，上式的可用 = 计算得到。这里表示序列中碱基的总个数，是为避免计算中出现零概率而引入的扰动。

3实验结果

我们在随机生成的模拟数据上对我们的程序进行了测试。随机生成t条满足均匀分布的DNA序列，在每条序列中植入（l， ）motif，即motif长度为l，发生个变异。对所实现算法的正确性，我们使用性能系数进行评估：

performace coefficient =

这里表示所植入的motif在序列中的位点集， 表示由算法所找到的motif在序列中的位点集。

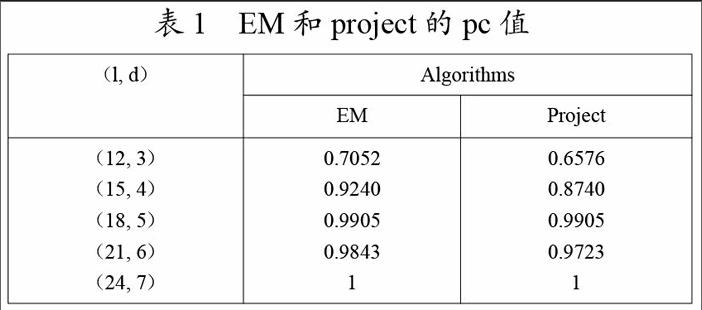
我们将我们的实现同project方法进行了比较，结果如表1所示：

表1 EM和project的pc值

表1中每项表示在十个样本上的平均的性能系数，其中每组包含20条数据，每条序列长为600。每轮测试进行10次迭代。对于（12， 3）、（15， 4）、 （18， 5）、（21， 6）、（24， 7），我们的实现的性能系数分别为0.6474、0.8740、0.9810、0.9723、1，同相应的project的方法相差不大，而它的性能系数分别为0.6576、0.8740、0.9905、0.9723、1。

同时，我们改变motif的长度，对两个算法的执行时间进行比较（单位：s），如表2所示：

表2 EM和project的运行时间

从表2中我们可以看出，我们的方法随着所找motif长度的增加，时间增长比较慢;而相应的project方法所用的时间增长很快。

参考文献

[1] Arthur Dempster， Nan Laird， and Donald Rubin. Maximum likelihood from incomplete data via the EM algorithm.Journal of the Royal Statistical Society，Series B，1977.39（1）：1-38.