用于压缩感知信号重建的SL0改进算法

齐焕芳,徐源浩

(西安电子科技大学 数学与统计学院,陕西 西安 710126)

用于压缩感知信号重建的SL0改进算法

齐焕芳,徐源浩

(西安电子科技大学 数学与统计学院,陕西 西安 710126)

SL0算法是一种基于近似l0范数的压缩感知信号重建算法,其思想是用一个光滑函数来近似l0范数,然后求解一个优化问题。目前采用的光滑函数都是高斯函数族,文中突破了以往采用高斯函数族近似l0范数,提出了采用复合三角函数作为近似估计l0范数的函数,然后结合修正牛顿法和阻尼牛顿法提出一种更精确的重建算法DNSL0。实验结果表明,在相同测试环境下,DNSL0算法在峰值信噪比和匹配度方面比SL0算法和NSL0算法都有了大幅提高。

压缩感知;重建算法;复合三角函数;近似l0范数;牛顿法

压缩感知理论(Compressive Sensing)[1-4]是一种全新的信号采样理论,它指出,只要信号是可压缩的或具有稀疏度,就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上,再通过求解一个优化问题就可以从这些少量的投影中以高概率重构出信号。该理论表明,通过采集少量的信号值就可以实现可压缩或稀疏信号的精确重构,克服了采样数据量大,采样时间以及数据存储空间等物理资源严重浪费的问题,具有良好的应用前景。目前用于压缩感知重建的算法从广义上主要分为两大方向:一是针对l0范数最小的;二是针对l1范数最小的。本文主要讨论l0范数最小化问题。

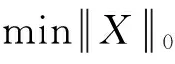
本文讨论的是SL0算法,它用光滑连续函数来近似l0范数,目前采用的是高斯函数族,致力于寻找优于高斯函数族的平滑连续函数来更精确地近似l0范数。因此,本文提出了基于SL0算法的一种新算法,用复合三角函数来近似估计l0范数,结合修正牛顿法和阻尼牛顿法获得的一种更精确、收敛速度更快的信号重构算法,称为DNSL0(DampNewtonSmoothl0Norm)算法。通过数值仿真,说明了该算法在峰值信噪比、匹配度和信噪比等方面的性能。

1 SL0算法

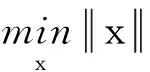
2 SL0算法的改进算法

2.1 改进算法近似估计l0范数

SL0算法的关键问题是选取合适的平滑连续函数来近似l0范数,通过求解连续函数的最小解使得l0范数最小。目前采用高斯函数族来近似l0范数,如采用高斯函数来近似l0范数[18],赵瑞珍等人提出用双曲正切函数来近似l0范数[19]。本文突破了以往采用高斯函数族近似l0范数,提出了逼近性能更好的非高斯函数族—复合三角函数作为近似估计l0范数的函数,其表达式为

(1)

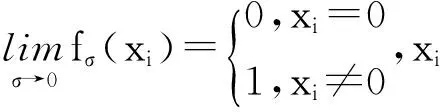
定义

(2)

l0范数指的是向量X中非零元素的个数,故l0范数可以近似表示为

(3)

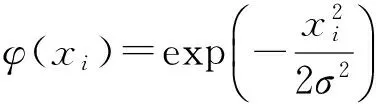
由图1中3个函数的分布可见,复合三角函数对近似l0范数的估计要好于1-高斯函数和双曲正切函数。在区间[-0.4,0.4]内,复合三角函数比高斯函数和双曲正切函数“陡峭性”更大,因此复合三角函数对l0范数的逼近要好于高斯函数和双曲正切函数。

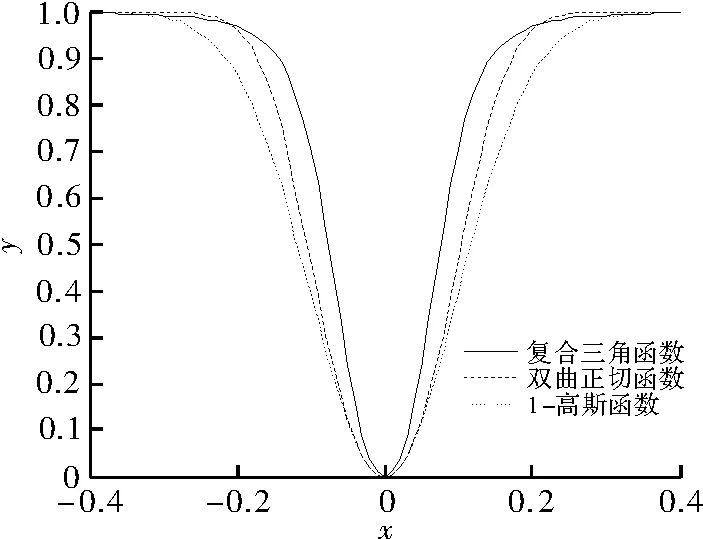
图1 σ=0.1两种函数对比图

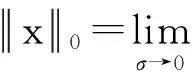
(4)

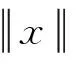
2.2 DNSL0算法具体实现

SL0算法采用高斯函数近似l0范数,将最小l0范数问题转化为凸优化问题,然后运用最速下降法求解该优化问题。由数学知识可知在搜索最优值过程中,搜索路径会出现“锯齿效应”,不能求得全局最优解,进而l0范数的估计精度降低。

针对以上问题,为了更好地近似估计l0范数以及提高算法的收敛速度,提出了用复合三角函数来近似l0范数,搜索方向为牛顿方向、步长因子由阻尼牛顿法求得的一种新的重建算法。

牛顿方向:d=-2Fσ(X)-1Fσ(X)。对式(2)取牛顿方向

(5)

(6)

从上述计算发现,该牛顿方向d中的Hesse矩阵不是正定矩阵,不能保证牛顿方向d为下降方向。为此,本文将通过对上述Hesse矩阵进行修正,得到一个修正的牛顿方向。

或

或

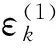
d=-G-1

(7)

综上,DNSL0算法的具体步骤如下:

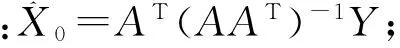
选择递减序列σ,[σ1,σ2,L,σS];

fors=1,2,K,S:

①σ=σs;

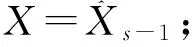
forj=1,K,L(最速下降法迭代次数)

a.搜索方向d=-G-1

b.阻尼牛顿法X←X+λd;

c.梯度投影X=X-ΦT(ΦΦT)-1(ΦX-Y);

3 实验结果及分析

为说明改进后算法的优良性,本文通过Matlab对该算法进行测试。

(1)对改进前后算法的性能做了比较。对512×512的Lena图像分别用SL0算法、NSL0算法和DNSL0算法进行重建,图2给出了重建后的直观视觉效果对比,压缩比为M/N=256/512=0.5。如图2所示,DNSL0算法的重建效果更好。

图2 SL0、NSL0和DNSL0重建效果对比

表1是不同的两幅图像,大小均为512×512,在压缩比为M/N=0.25下,SL0算法、NSL0算法和DNSL0算法在峰值信噪比、相对误差和匹配度之间的对比。DNSL0算法得到的数据取的是在该代码运行100次得到的结果取平均值。SL0算法和NSL0算法的数据参考文献[20]中的数据。

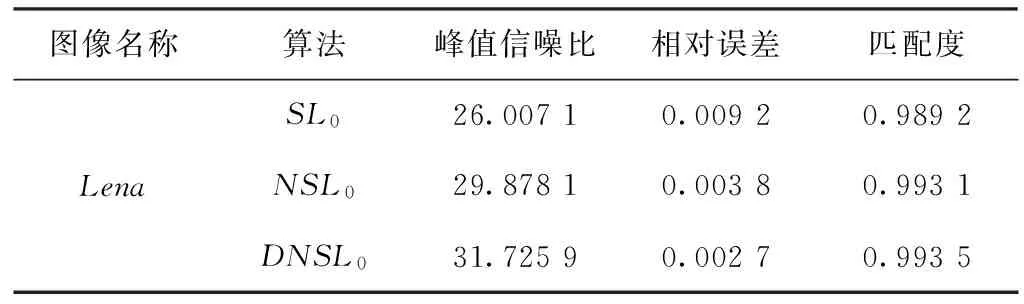
表1 SL0、NSL0和DNSL0重建质量比较

由表1可以看出,DNSL0算法与NSL0算法相比,峰值信噪比平均提高了2.2dB,相对误差平均减少了0.22%,匹配度也有所提高。

(2)在相同的压缩比M/N=0.5的情况下,对DNSL0算法和其他常用的重建算法进行比较。表2所示为Lena图像在不同算法下重建质量对比,从此表中可以明显看出DNSL0算法相比传统压缩感知重建算法在各方面性能均有较大提高。

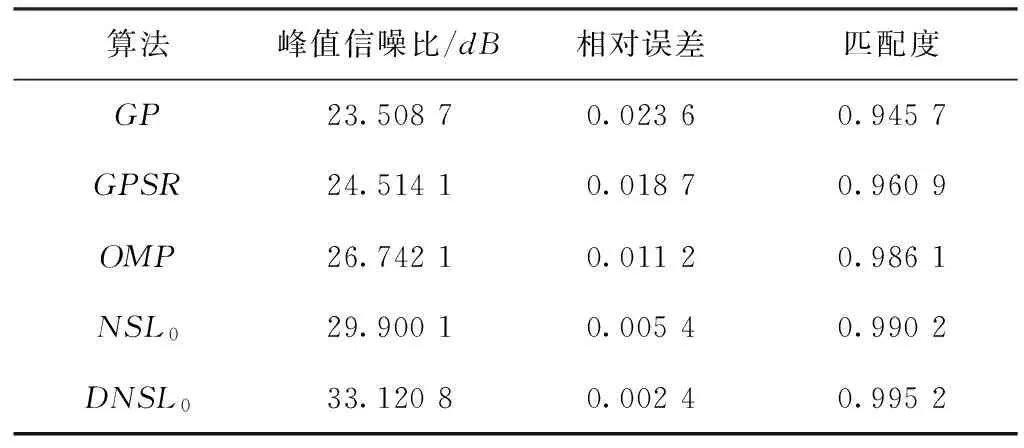
表2 各算法重建质量对比

各种实验结果表明,DNSL0算法用复合三角函数通过递减序列σ的逐步逼近来近似l0范数,能有效地实现l0范数的近似,从而改进了重建质量。另外,采用修正牛顿法求解比最速下降法收敛速度更快,并有效防止“锯齿现象”。

4 结束语

目前,SL0算法中近似l0范数估计函数选取的均为高斯函数族,如1-高斯函数、双曲正切函数、近似双曲正切函数等。本文选取了重建性能更好的复合三角函数来近似l0范数,结合修正牛顿法和阻尼牛顿法提出了一种DNSL0算法。实验结果表明,DNSL0算法是一种综合性能较好的重建算法。三角函数族中是否有更好的函数来逼近l0范数将是下一步需要继续研究的问题。

[1]CandésE.Compressivesampling[C].Zürich,Switzerland:ProceedingsofInternationalCongressofMathematicians,EuropeanMathematicalSocietyPublishingHouse,2006,21:1433-1452.

[2]BaraniukR.Compressivesensing[J].IEEESignalProcessingMagazine,2007,24(4):118-121.

[3]ZhaoRuizhen,LiuXiaoyu,LiChingchung.Waveletdenoisingviasparserepresentation[J].ScienceinChinaSeriesF,2009,52(8):1371-1377.

[4]CandèsE,RombergJ,TaoT.Stablesignalrecoveryfromincompleteandinaccuratemeasurements[J].CommunicationsonPureandAppliedMathematics,2006,59(8):1207-1223.

[5]JeevanKPant,LuWusheng,AndreasAntoniou.Reconstructionofsparsesignalbyminimizingare-weightedapproximatel0-norminthenullspaceofthemeasurementmatrix[J].IEEETransactionsonSignalProcssing,2005,53(8):3010-3022.

[6] 贺亚鹏,李洪涛,王克让,等.基于压缩感知的高分辨DOA估计[J].宇航学报,2011,32(6):1344-1349.

[7]ChenS,DonohoDL,SaundersMA.Atomicdecompositionbybasispursuit[J].SLAMJournalScienceComput,2001,43(1):129-159.

[8]ChenS,DonohoD.Basispursuit[C].Monterey,CA:Proceedingof28thAsilonmarConferenceSignals,SystemComputer,1994.

[9]WangY,YinW.Sparsesignalreconstructionviaiterativesupportdetection[J].SLAMJournalonImagingSciences,2010,3(3):462-491.

[10]DonnhoDL.Formostlargeunderdeterminedsystemsoflinearequationstheminimall1-normSolutionisalsothesparsestsolution[J].CommunicationPureApplication,2006,59(6):797-829.

[11]TroppJ,GilbertA.Signalrecoveryfromrandommeasurementsviaorthogonalmatchingpursuit[J].IEEETransactionsonInformationTheory,2007,53(12):4655-4666.

[12]NeedellD,VershyninR.Signalrecoveryfromincompleteandinaccuratemeasurementsviaregularizedorthogonalmatchingpursuit[J].IEEEJournalSel.TopicsSignalProcess,2010,4(2):310-316.

[13]DaiW,MilenkovicO.Subspacepursuitforcompressivesensingsignalreconstruction[J].IEEETransactionsonSignalProcessing,2009,55(5):2230-2249.

[14]NeedellD,TroppJ.CoSaMP:Iterativesignalrecoveryfromincompleteandinaccuratesamples[J].ApplicationofOmputimoArmon,2009,26(2):301-321.

[15]RodriguezP,WohlbergB.Aniterativereweightednormalgorithmfortotalvariationregularization[J].IEEESignalProcessingLetters,2007,14(12):948-951.

[16]ChartrandR,YinW.Iterativereweightednormalgorithmforcompressivesensing[J].Acoustics,SpeechandSignalProcessing,2008(6):3869-3872.

[17]MohimaniGH,Babaie-ZadehM,JuttenC.Fastsparserepresentationusingsmoothednorm[J].IEEETransactiononSignalProcessing,2007,46(6):1-12.

[18]MohimaniGH,Babaie-ZadehM,JuttenC.Afastapproachforovercompletesparsedecompositionbasedonsmoothednorm[J].IEEETransactiononSignalProcessing,2009,57(1):289-301.

[19]赵瑞珍,林婉娟,李浩,等.基于光滑l0范数和修正牛顿法的压缩感知重建算法[J].计算机辅助设计与图形学学报,2012,24(4):478-484.

[20]杨良龙.基于SL0压缩感知信号重建的改进算法[J].信号处理,2012,28(6):834-841.

Improved SL0Algorithm for Compressive Sensing Signal Reconstruction

QI Huanfang,XU Yuanhao

(School of Mathematics and Statistics,Xidian University,Xi’an 710126,China)

The smoothedl0norm algorithm (SL0) is a reconstruction algorithm in compressive sensing based on approximatel0norm.It is to use a smooth function to approximate thel0norm and then solve an optimization problem.Currently people use the Gauss family function as a smooth function.This paper makes a breakthrough in the use of the composite trigonometric function,instead of the traditionally used Gauss family function,which is used to approximate thel0norm.And a new efficient and more accurate algorithm named DNSL0(Damp Newton Smoothl0Norm) is proposed based on the smoothedl0norm and the revised Newton method and the damped Newton method.Experimental results show that the DNSL0algorithm is greatly improved in both the peak value signal-to-noise ratio and matching degree compared with the SL0algorithm and NSL0algorithm under the same experimental conditions.

compressive sensing;reconstruction algorithm;composite trigonometric function;approximatel0norm;Newton method

2014- 08- 21

齐焕芳(1988—),女,硕士研究生。研究方向:压缩感知重建方法。E-mail:983036383@qq.com。徐源浩(1989—),男,硕士研究生。研究方向:图像处理。

10.16180/j.cnki.issn1007-7820.2015.04.008

TN911.73;TP391.41

A

1007-7820(2015)04-027-04