基于判别低秩矩阵恢复和稀疏表示的车标识别

曹蒙蒙，李新叶，范月坤

(华北电力大学电子与通信工程系，河北保定 071003)

车辆识别是智能交通系统的重要研究内容。随着汽车数量的增加，汽车假牌、套牌等现象越来越多。这就对车辆识别研究提出更高的要求，即在识别车牌号码的同时也要识别出车型，若要确定车牌与车型的一致性，即鉴别是否为套牌车辆。因此，基于交通图像的车标识别因其在公共安全中的重要意义受到越来越多的关注。关于车辆类型的研究，现在主要集中在识别大型货车、中型汽车、小型轿车的范围［1－2］。对车辆所属的具体车型进行识别难度较大，对于车辆品牌的识别，有些采用车的前脸作为研究对象进行车型识别［3］，但由于详尽车型的车脸特征不突出，因此识别率低。通常采用车标识别的方法来实现。

目前国内外学者已在车标识别方面进行了相关的研究，例如文献［4］使用模版匹配的方法进行车标识别，文献［5］中采用模版匹配进行粗识别然后采用特征进行二次识别，文献［6］提出了基于 Hu不变矩的识别方法，文献［7］利用独立成分分析提取车标的特征然后采用模糊支持向量机实现车标分类，D.F.Llorca等人提取车标的HOG特征并采用支持向量机进行车标识别［8］。

然而，由于许多非理想条件(天气，反光、车辆运动、车辆表面污损等)，导致采集到的车标图像不理想，而上述方法没有考虑到图像本身质量差带来识别率低的问题。由于阴影、反光、遮挡、污损等原因使得实际获取的图像低秩结构被破坏，影响分类性能。文献［9～10］对矩阵的低秩恢复进行了研究。针对车标识别中图像质量不理想的情况，本文提出将判别低秩矩阵恢复的思想应用于车标识别，通过向字典学习的目标函数中添加一个理想编码的正则项，将类别标签信息纳入字典学习的过程，使得学习到的用于稀疏表示的字典具有良好的重构性和判别力，同时学习一个低秩投影矩阵将测试样本投影到相应的底层子空间来去除测试样本中可能的破坏，然后利用基于最小重建误差的稀疏表示进行车标识别。

1 稀疏表示分类算法

近年来，以信号重构误差最小化为目标、约束表示系数的稀疏性的稀疏表示模型，以其强大的信号表示能力被广泛应用于信号处理与模式识别中。Wright等人［11］稀疏表示分类应用于人脸识别中。其核心思想是寻找测试样本在字典中最稀疏的原子表示，即用最少数目训练样本的线性组合来表示测试样本。假定有k类样本，每一类样本包含n个训练样本，用矩阵D=［D1，D2，…，Dk］表示原始的训练样本，其中 Di表示第i 类训练样本 Di=［Di，1，Di，2，…，Di，n］，Di，j表示第 i类中第j个样本的特征向量。y表示测试样本，对测试样本进行稀疏表示分类步骤如下:

(1)编码阶段。通过l1范数最小化在字典A上对y进行稀疏编码

其中，γ是一个正数，为一个标量。

(2)分类阶段。通过式(2)进行分类

2 判别低秩矩阵恢复

由于阴影、反光、遮挡等的影响，实际获取的车标图像低秩结构被破坏，影响分类性能。因此，有效地从具有噪声的图像中恢复低秩车标子空间，即去除样本中由于遮挡、光照等因素而产生的严重误差，是提高识别效果的关键。从损坏的训练图像样本中恢复一个干净的字典用于稀疏表示就要用到低秩矩阵恢复(LRR)。由于最基本的低秩矩阵恢复算法［12］不具有判别性，并不适合分类识别。为更好地进行分类，向字典学习的目标函数中添加一个理想编码的正则项，将类别标签信息纳入字典学习的过程，使得判别低秩矩阵恢复的用于稀疏表示分类的字典具有判别性。

2.1 判别低秩矩阵恢复

给定一个由类车标样本组成的数据矩阵X=［X1，X2，…，XN］，其中 Xi对应第 i类样本，X 可能包含噪声。低秩矩阵恢复可将X分解为一个低秩的部分DZ和稀疏的噪声部分E，即X=DZ+E。对于字典D，数据矩阵X的最优表示矩阵Z应该是分块对角矩阵

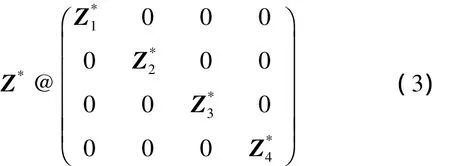
字典 D=［D1，D2，…，DN］包含 N 个子字典，其中Di对应于第 i类。令 Zi=［Zi，1，Zi，2，…，Zi，N］为 Xi在字典D中的表示系数。为获得一个低秩且稀疏的数据表示，每个类i应该能被其子字典较好地表示，即Xi=DiZi，i+Ei，而 Zi，j为其在子字典 Dj(i≠j)的系数，其几乎为0。假设 Q 为最理想的表示系数，Q=［q1，q2，…，qT］∈RK×T，这里 qi为样本 xi的表示系数，它的形式为［0…1，1，1，…］t∈Rk，其中 K 为字典的尺寸，T 为总样本数。假定xi属于第L类，则其在子字典DL上的系数全部为1，在其他子字典上的系数全部为0。例如假定字典 D=［d1，d2，…，d6］即字典有 6 个原子，数据矩阵为 X=［X1，X2，X3］即包含3 类样本，若第一类 X1包含3 个样本 x1，x2，x3，第二类 X2包含两个样本 x4，x5，第三类 X3包含 4 个样本 x6，x7，x3，x9，则 D 有 3 个子字典，每个字典有两个原子。则Q表示为

由以上的定义，基于标签信息为训练样本构造一个块对角形式的矩阵Q。添加正则项将结构化信息融入到字典训练中。则字典学习的目标函数便可写为

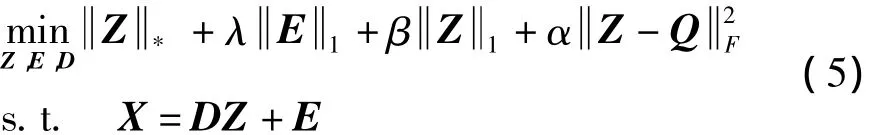
其中，λ和β分别控制噪声矩阵E和表示系数矩阵Z的稀疏性;α为调整因子控制正则项分别代表矩阵的核范数和l1范数。本文采用自适应罚项线性化交替方向法(LADMAP)［13］解决上述目标函数的优化问题。在解决上述优化问题时引入辅助变量W使目标函数可分，则目标函数(5)可写为

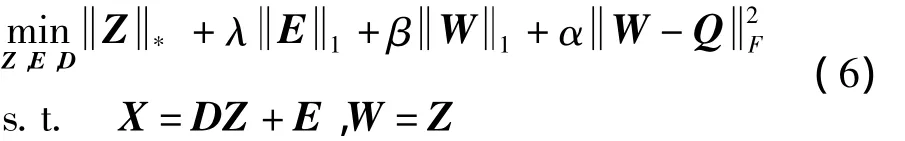
根据LADMAP来求解Z和E那么增强的拉格朗日函数可写为

通过每次固定其他两个，更新Z，W，E其中一个变量来进行函数优化

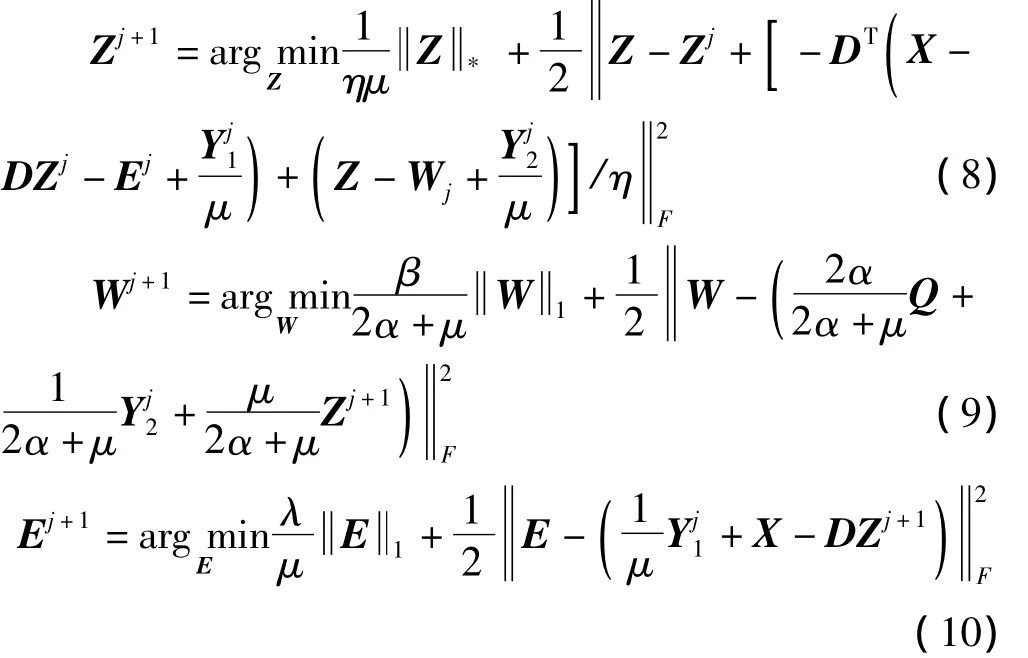
算法1 低秩矩阵恢复优化算法。

输入:数据X字典D，参数λ，β和α。

输出:Z，E，W。

初始化:Z0=W0=E0=Y01=Y02=0，β=1.1，ε=10－7，μmax=1030执行以下循环直到满足停止条件(not converged，Z≤maxIter Z)。

通过式(8)固定W、E更新Z

通过式(9)固定Z、E更新W

通过式(10)固定Z、W更新E

更新乘子

更新μ:

μ =min(μmax，ρμ)

check the convergence conditions:

end while

经过判别低秩矩阵恢复后的训练样本可分为两部分，即纠正后的样本和稀疏误差。纠正后的样本作为字典进行稀疏表示，比原始的训练样本具有更强的判别力和重构性能力。

2.2 低秩矩阵映射

通过上述判别低秩矩阵恢复可以得到一个具有良好重构性和判别力的干净的车标稀疏表示字典，但是通常采集到待识别的车标也同样存在噪声。文献［14］提出，学习一个低秩投影矩阵，通过将测试样本投影到相应的底层子空间来纠正低秩结构被破坏的测试样本。因此，文中假设P是一个低秩投影矩阵，其将数据X投影到相应的底层子空间，产生低秩子空间恢复结果为PX。可通过解决以下优化问题来获得映射矩阵P

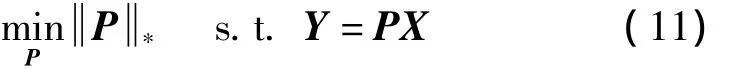
假定P*是上述问题的最优解，分别计算P*X和X－P*X便可得到样本X的主要成分和误差部分。上述目标函数的最优解为P*=YX+，其中X+是X的伪逆矩阵。伪逆矩阵定义为X+=V∑－1UT，这里X是V∑UT的瘦形奇异值分解(skinny SVD)。

2.3 车标识别

由以上分析可知，有效地从具有噪声的训练图像中恢复车标，即去除训练样本中遮挡、光照，污损等严重误差，同时对训练样本进行低秩矩阵恢复得到干净的测试样本，是稀疏表示分类算法更具鲁棒性的关键。本文提出的基于判别低秩子空间恢复的稀疏表示车标识别算法步骤如下:

(1)将所有训练样本的特征向量组合成训练样本集X，测试样本的特征向量为y。

(2)本文中选择训练样本矩阵作为初始字典进行低秩矩阵恢复。则目标函数可写为

对目标函数(12)采用LADMAP方法进行优化后得到最优的低秩矩阵Z*和误差矩阵E*。从而获得低秩矩阵恢复后的训练样本XZ，将其用于后面稀疏表示的字典。

(3)根据式(11)计算最优低秩映射矩阵P*，将测试样本y通过yp=P*y投射到其相应的子空间，从而得到干净的测试样本yp。

(4)在低秩矩阵恢复后用于稀疏表示的字典和测试样本yp分别进行PCA降维。然后根据式(1)进行稀疏表示，得到稀疏表示系数α^i。

(5)根据式(2)，测试样本y被识别为重构误差最小的那一类。

3 实验结果及分析

实验采用的数据库由大众、现代、奥迪等20类样本组成，每类样本包含60个车标图像，这些图像一部分源自于数据库Medialab LPR Database，一部分为路口交通拍摄图片分的车标图像，包括一些倾斜、残缺、模糊、遮挡等非理想情况下的车标图像，图像全部归一化为50×50，图1为部分车标样本。

图1 部分车标样本

将本文算法与文献［6，8］中传统的SRC算法进行对比试验，实验中参数 λ=16，β=15，α=500，γ=0.15，分类结果如表1所示。

表1 不同算法的识别率比较

实验时，采用主成分分析的方法对纠正后的训练样本和测试样本分别进行特征降维，为测试不同特征维数对实验性能的影响，分别选择维数 d=30、80、130、180、230、280进行实验。图3为选取不同的特征维数时，本文方法与SRC方法对比的识别结果。可看出，基于判别低秩矩阵恢复的稀疏表示算法明显优于SRC识别方法。同时，如图2所示在维数d=230时取得了较好的识别结果。

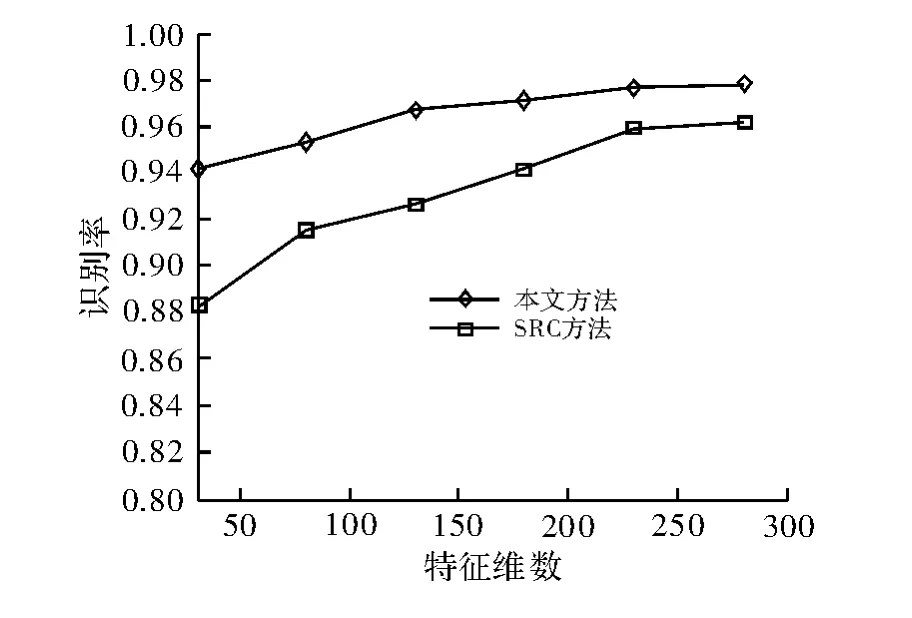
图2 不同算法的特征维数与识别率关系曲线

为测试不同的训练样本数对识别结果的影响，每类中分别随机选择 5、10、15、20、25、30 幅图像作为训练样本，剩余图像用于测试，采用随机选择训练样本的方式可以保证实验结果不依赖于某种特定的训练数据选择。实验结果如表2所示。

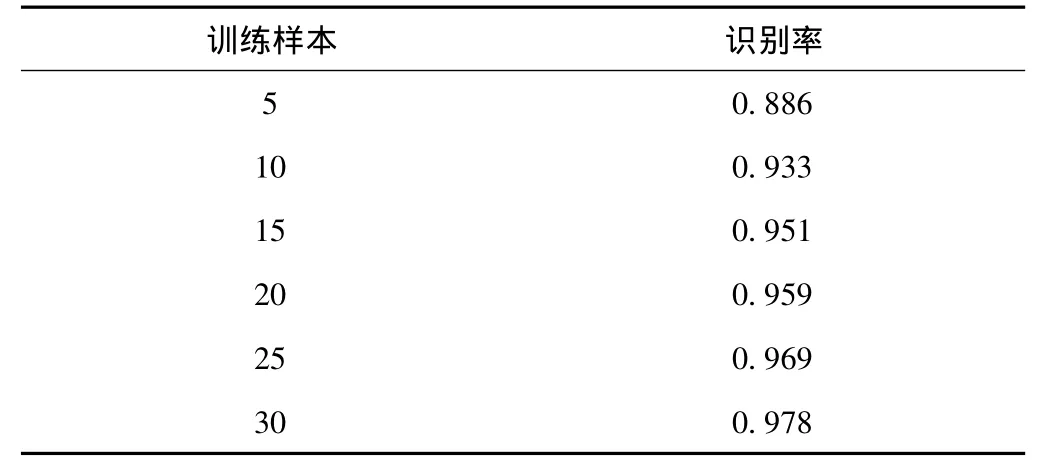
表2 不同训练样本数时的识别率

为更加直观，采用文献［7～8］与SRC的方法作为基准，与本文方法进行比较。图3给出了几种识别方法在不同数量的训练样本时的识别率变化曲线。如图3所示，相对于其他分类算法，无论从每类样本中随机选择多少幅图像用来训练，本文算法都取得了较好的识别结果。

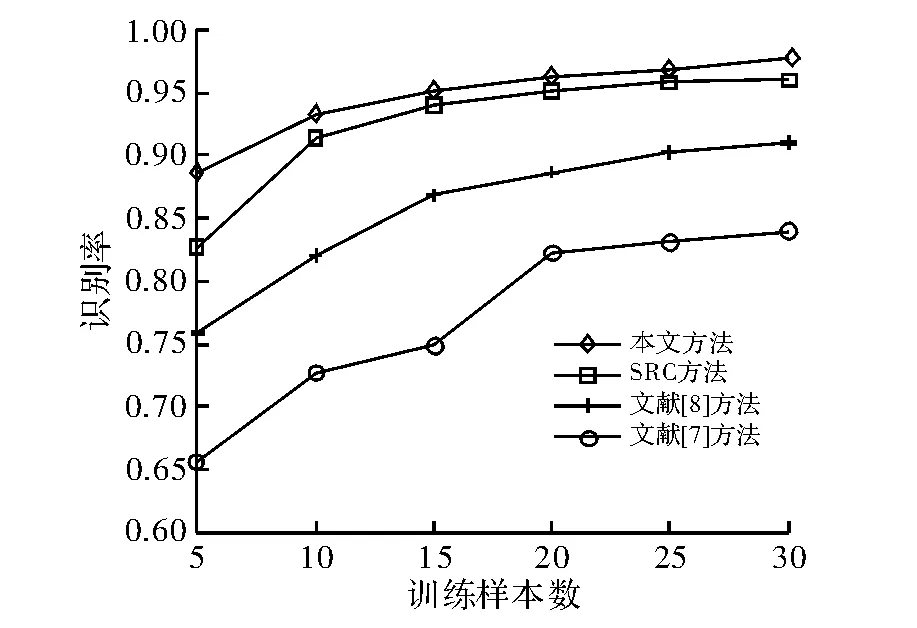
图3 不同算法训练样本数与识别率曲线

4 结束语

车标识别是一个具有广阔前景，并具有挑战性的课题。由于交通图像的采集受到外界环境、遮挡以及污损等因素的影响，实际获取的车标图像较少表现出低秩结构，影响分类性能。针对该问题，本文提出基于判别低秩矩阵恢复的稀疏表示车标识别方法，通过在低秩矩阵恢复的目标函数中添加正则项，将类别标签信息纳入字典学习过程，学习得到一个有判别力的字典对训练样本进行低秩矩阵恢复，同时学习一个低秩投影矩阵将测试样本投影到相应底层子空间，来去除测试样本中的错误，最后在此基础上利用稀疏表示分类方法进行分类判别，实验结果表明，该方法有较好的识别结果。

［1］唐朝霞，俞扬信，张粤.基于粒子群算法和云模型的车型识别［J］.微电子学与计算机，2013，30(11):80 －83.

［2］华莉琴，许维，王拓，等.采用改进的尺度不变特征转换及多视角模型对车型识别［J］.西安交通大学学报，2013，47(4):92－99.

［3］张小琴，赵池航，沙月进，等.基于HOG特征及支持向量机的车辆品牌识别方法［J］.东南大学学报:自然科学版，2013，43(A02):410 －413.

［4］曹刚.运动车辆识别技术研究［D］.成都:四川大学，2004.

［5］罗彬，游志胜，曹刚.基于边缘直方图的快速汽车标志识别方法［J］.计算机应用研究，2004，21(6):150 －151.

［6］刘嘉敏，路昆.基于Hu不变矩的车标识别［J］.科技信息:学术研究，2008(1):464 －466.

［7］孙娟红，李文举，冯宇，等.基于独立成分分析和模糊支持向量机的车标识别新方法［J］.微型机与应用，2011，30(13):32－35.

［8］Llorca D F，Arroyo R.Vehicle logo recognition in traffic images using HOGfeatures and SVM［C］.Hague:2013 16th International IEEE Conference on Intelligent Transportation Systems－(ITSC)，2013:2229－2234.

［9］Wright J，Li X，Ma Y，et al.Robust principal component analysis?［J］.Journal of the ACM(JACM)，2011，58(3):11.

［10］Chen CF，Wei CP，Wang Y CF.Low －rank matrix recovery with structural incoherence for robust face recognition［C］.Portland，OR:2012 IEEE Conference on Computer Vision and Pattern Recognition(CVPR)，2012:2618 －2625.

［11］Wright J，Yang A Y，Ma Y，et al.Robust face recognition via sparse representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31(2):210 －227.

［12］Liu G，Lin Z，Yan S，et al.Robust recovery of subspace structures by low －rank representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2013，35(1):171－184.

［13］Zhuang L，Gao H，Lin Z，et al.Non － negative low rank and sparse graph for semi－ supervised learning［C］.Providence，RI:2012 IEEE Conference on Computer Vision and Pattern Recognition(CVPR)，2012:2328 －2335.

［14］Bao B K，Liu G，Xu C.Inductive robust principal component analysis［J］.IEEE Transactions on Image Processing，2012，21(8):3794－3800.