基于改进A*算法的水下航行器自主搜索航迹规划
荣少巍
(昆明船舶设备研究试验中心 第1研究室,云南 昆明 650051)
基于改进A*算法的水下航行器自主搜索航迹规划
荣少巍
(昆明船舶设备研究试验中心 第1研究室,云南 昆明 650051)
以水下航行器在水下路径规划为研究重点,提出了基于改进型A*算法的水下无人航行器自主搜索航迹规划算法。一般航迹规划可由多种算法完成,而在这些算法中以A*的计算流程最为简单、算法易于实现,并在理论上可保证全局最优解的收敛性;且程序较为简短,可在一些低功耗、低主频的系统中应用。由于传统的A*算法不具备最小转弯半径等约束条件,因此,针对水下航行器高低速问题,对传统的A*算法进行改进,使得A*算法可实现高速与低速相结合的应用。
水下航行器;A*算法;航迹规划
无人飞行器已在航空领域大量应用,在水下航行器领域,无人航行器也开始展开应用,无人水下航行器得到了关注。而无人水下航行器在水下如何避障成为了研究水下航行器路径规划的重点。
目前在航迹规划领域中,通常有包含A*搜索算法[1-3]、动态规划Dijkstra算法、遗传算法、粒子群算法、数学最优规划[8]等。在所有这些算法中,A*的计算流程最为简单且最易实现,并在理论上可保证全局最优解的收敛性。此外,程序也较简短,可在一些低功耗低主频的系统中应用。因此,A*算法得到了广泛的应用。
本文提出基于改进型A*算法的水下无人航行器自主搜索航迹规划算法。传统的A*算法没有最小转弯半径等约束等条件。然而水下航行器的运动特点却不同,既有低速、小转向半径或者零转向半径的航行器,也有高速大转向半径的航行器,这一点与传统的基于无人机的A*搜索算法不同,因此需要对传统的A*算法进行改进,使得A*可以实现高速与低速结合的应用。本算法正是针对小型水下航行器的特点进行了改进A*算法研究与仿真,该算法可以较好地规避障碍,并能以最优路径进行目标搜索,因此具有较好的应用前景。
1 A*算法基本原理
A*算法的基本原理是一种启发式的图搜索算法,能够满足航迹规划中不同约束条件的要求,在满足这些条件下可计算得到一个最优的路径解。而且A*算法在理论上可得到一个完全收敛的结果,且只需最少的扩展点数即可完成计算,这样对硬件计算能力的要求也最低,可利用最少的资源进行复杂的路径规划任务。
A*算法的代价函数表示为
f(n)=g(n)+h(n)
(1)
其中,f(n)是节点n从初始点到目标点的估价函数;g(n)是在状态空间中从初始节点到n节点的实际代价;h(n)是从n到目标节点最佳路径的估计代价。保证找到最短路径条件,关键在于估价函数h(n)的选取:
(1)估价值h(n)≤n到目标节点的距离实际值,这种情况下,搜索的点数多、搜索范围大、效率低,但能得到最优解。
(2)若估价值>实际值,搜索的点数少、搜索范围小、效率高,但不能保证得到最优解。
因此,h(n)也被称为启发函数,故在实际搜索应用中不能需要对启发函数按实际操作进行修正才可能得到一个较好地应用。
针对这种启发式的搜索方式,在算法中加入了类似于游戏地图的模式,即close/open模式。这种模式的原理在于,将一个未知需要搜索的地域划分为N个方格,探测器一次可探测一个方格的内容,一旦被探测器探测过的区域,这个区域就被记录于open的数据库中,而未被探测的未知地域则被记录在close数据库中,通过不重复的搜索过程,最终通过最优路径到达目的地。
2 高速水下航行器运动建模
传统的A*算法将一个区域划分为方块区域,因此一个点就有8个区域方向或是扩展为24个区域方向可选的路径。如图1和图2所示。
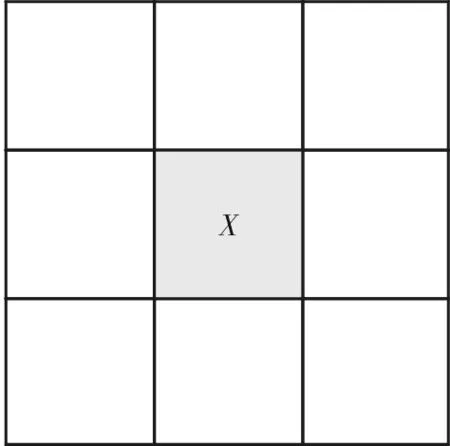
图1 8方向分割图

图2 24方向分割图
8方向与24方向都是没有考虑高速运动物体的运动特性而确定的理想方式,这种模式针对低速或零转向半径的航行器可适用,而针对高速水下航行器则不能较好地运用。因此针对高速水下航行器,需要对其运动进行建模,然后确定其方向状态模式。
搜索区域为一个较大的区域,而水下航行器相对于搜索区域来说显得较小,可认定为一个质点。
水下航行器的实际运动方程较为复杂,在路径规划中无需如此复杂的运动方程,因此进行了简化。设某一水下航行器在一固定深度航行,其运动方程为
θn+1=θn+θΔ
(2)
xn+1=xn+Ccos(θΔ+1)
(3)
yn+1=yn+Ccos(θΔ+1)
(4)
式(2)中,θn为当前水下航行器的航向角;θn+1为下一时刻的航向角;xn+1,yn+1为下一时刻的坐标,这个坐标的变化量为前一时刻坐标加上航向角的变量,如图3所示。
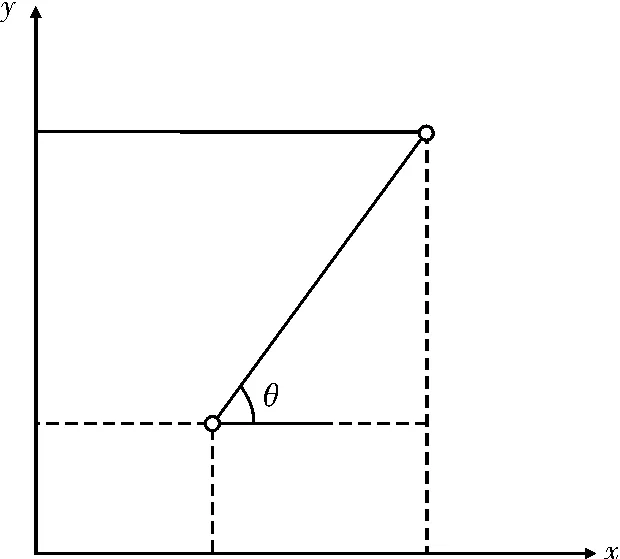
图3 运动位置改变量示意图
而高速的物体在水下进行转向则需要较大的转向半径,最小转向半径的近似计算公式为
(5)
θmax=arcsin(Co/(2Rmin))
(6)
式(6)表明了最大航向角改变量与最小转向半径成非线性反比关系。
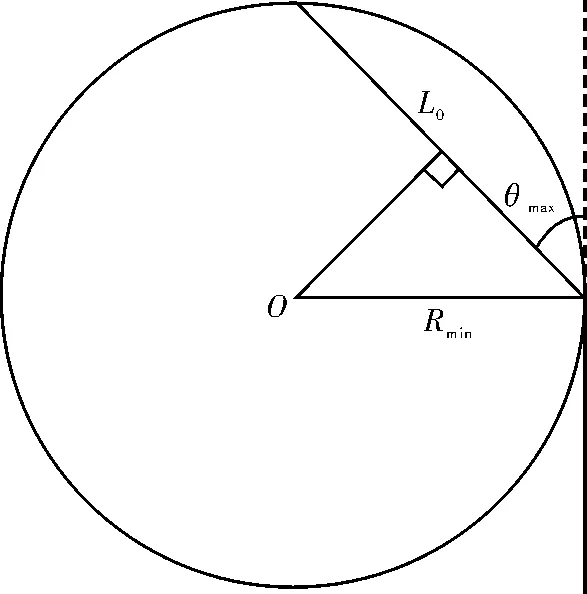
图4 最大航向角改变量与最小转向半径计算示意
3 改进A*搜索算法
A*搜索算法的代价函数由式(1)给出,其中g(n)为水下航行器运动的起点至目前n点位置的真实代价,再加入一个最小的估计代价函数h(n),就可以得到完整的代价函数。其中真实代价函数表示为
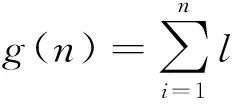
(7)
式(7)中,l为当前路径的长度,真实的代价函数就表示为总的路径长度。
而在一个区域中,如果进行搜索前进,则在全局中的最优解必然是两点之间的直线为最优解,表示为
(8)
采用式(8)的两点间直线距离公式作为A*算法的启发函数,这样可以保证航行器在理论上从起点至终点的航行距离最小,即代价函数的值最小。
改进A*算法的基本的基本计算步骤为:
首先确定目标位置,根据目标位置,确定航行器的起点为起始节点,目标位置为终止节点,每个节点的大小由航行器避碰的探测能力确定,航行器航行路径为式(8)确定的最优解。
再次,将航行路径中的所有区域设定为未知区域节点,放入close数据库中;当航行器经过任意一个区域节点,该节点就放置于open数据库中。
如果在探测过程中发现前方有节点为障碍节点时,应当沿障碍节点的边沿进行规避,规避过程中需根据运动方程所确定的最小转向半径进行规避,如果是拥有零转向半径的水下航行器,则可沿直角或任意角度进行转向。
在进行转向前,再次对路径进行规划,首先以当前节点作为起点,以最小代价函数为路径,再次判断至下一节点能否以直线前进,而不与障碍相交,若通路的直线视线没有被遮挡,则可直接通过,无需进行转向,沿直向前行,确保路径最短,路径优化原理如图5所示。
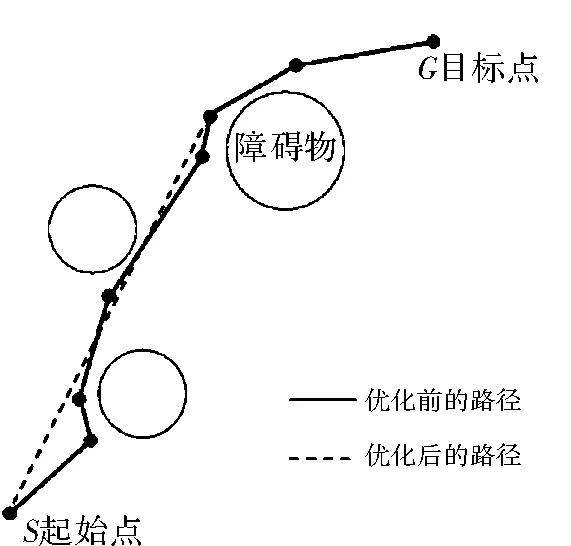
图5 路径优化原理
4 算法仿真
算法仿真采用Matlab进行,图6为整个仿真的区域图,其中圆点区域为障碍区域,+字符号为水下航行器前进路径,其余为无障碍水域。在仿真设置中,加入了横向纵向的障碍,且障碍交替出现,由起点至终点无法通过单一直线路径到达,需经过多次转向才能到达,因此增加了路径规划的难度,可较好地对高速低速水下航行器路径规划进行仿真。路径规划仿真结果如图6所示。
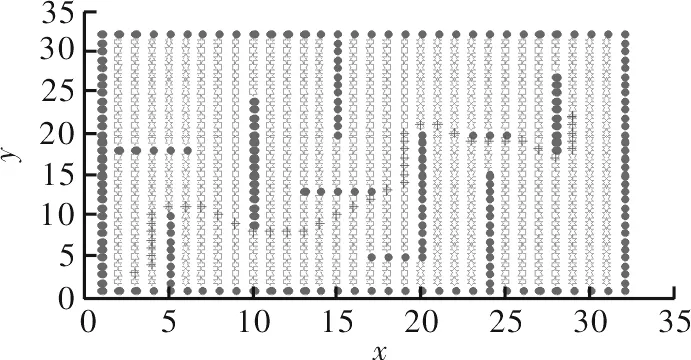
图6 路径规划仿真图
在仿真过程中采用未优化的传统A*算法仿真的路径如图7所示,其中出现一些很大的直接转向路径,这也模拟了低速或零转向半径的水下航行器的运动轨迹。从图中可看出,转向出现了许多折线部分,这在低速与零转向半径的航行器可使用,但高速物体的转向不能出现角度较大的折线。

图7 未优化路径结果输出
优化前后的高速水下航行器路径规划算法仿真如图8所示,实线为传统算法加入部分优化后的路线,从中还是可看到较为大幅的转向,这个在实际当中不能较好地为高速航行器进行路径规划,而虚线则利用改进A*算法结合高速航行器运动方程进行优化的路径,这里面完全没有了折线的出现,且曲线也较实线平滑,更适合于高速水下航行器的运动。
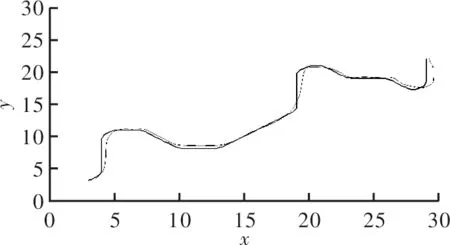
图8 优化前后高速航行器路径结果输出
5 结束语
本文叙述了基于改进型A*算法的水下无人航行器自主搜索航迹规划算法。克服了传统A*算法没有最小转弯半径等约束等条件的缺陷。结合水下航行器的运动方程的特点,对传统的A*算法进行改进,使得A*可实现高速与低速结合的应用。本算法针对小型水下航行器的特点进行了改进A*算法的研究与仿真,该算法可较好地规避障碍,并能以最优路径进行目标搜索,具有较好的应用前景。
[1]SenthilArumugamM,RaoMVC,AarthiChandramohan.Anewandimprovedversionofparticleswarmoptimizationalgorithmwithglobal-localbestparameters[C].KnowlInformationsystem,2008(16):331-357.
[2]SzczerbaRJ.Robustalgorithmforalgorithmforrealtimerouteplanning[J].IEEETransactiononAerospaceandElectronicSystem,2000,36(3):869-878.
[3] 符小卫,高小光.一种无人机路径规划算法研究[J].系统仿真学报,2004,16(1):20-21.
[4] 诸静.模糊控制原理及应用[M].北京:机械工业出版社,1999.
[5] 徐德民.鱼雷自动控制系统[M].2版.西安:西北工业大学出版社,2001.
[6]ChenLD,ToruS.Dataminingmethods,applications,andtools[J].InformationSystemManagement,2000,17(1):65-70.
[7] 杜萍,杨春.飞行器航迹规划算法综述[J].飞行力学,2005,23(2):10-14.
[8] 张旭东,李文龙,胡良梅,等.基于PMD相机的特征跟踪位姿测量方法[J].电子测量与仪器学报,2013(7):26-30.
[9] 马云红,周德云.基于B样条曲线的无人机航路规划算法[J].飞行力学,2004,22(2):74-77.
[10]郑睿;孟晓风;聂晶,等.基于VXI总线的QCM测试系统设计与实现[J].电子测量与仪器学报,2012(8):77-79.
[11]WilliamsWJ,JeongJ.Newtime-frequencydistribution:Theoryandapplications[C].ProceedingofIEEEICASSP-89,1989:1243-1247.
Research of Underwater Autonomous Search Path Planning Based on Improved A*Algorithm
RONG Shaowei
(First laboratory,Kunming Shipborne Equipment Research & Test Center,Kunming 650051,China)
This paper studies the underwater path planning of the underwater vehicle.It puts forward an underwater unmanned underwater vehicle autonomous search path planning algorithm based on the improved A*algorithm.The general path planning can be done by a variety of algorithms.Among them,the A*algorithm is simple and easy to realize,and can theoretically guarantee the convergence of the global optimal solution;and its program is simple,so that it can be used in the system of low power consumption and low frequency.Because the traditional A*algorithm does not have the minimum turning radius and other constraints,we improve the traditional A*algorithm since underwater vehicles run either at a high or at a low speed,so that it can be applied in both cases.
Underwater vehicle;A*algorithm;path planning
2014- 08- 28
荣少巍(1986—),男,硕士,助理工程师。研究方向:嵌入式系统。E-mail:formulaf11986@163.com
10.16180/j.cnki.issn1007-7820.2015.04.005
TP306.1
A
1007-7820(2015)04-017-04

