元胞遗传算法的多样性研究
林志龙,鲁宇明
(南昌航空大学 信息工程学院,江西 南昌 330063)
元胞遗传算法的多样性研究
林志龙,鲁宇明
(南昌航空大学 信息工程学院,江西 南昌 330063)
探讨了元胞遗传算法中种群多样性对全局寻优/局部收敛平衡的意义,提出了基于邻域结构内元胞遗传算法的多样性度量方式,并提出了改变遗传算子的元胞遗传算法来维持进化过程种群的多样性,算法将元胞空间网格嵌入到种群空间中,模拟遗传操作在相邻个体之间进行。该算法不仅提高了全局搜索能力,且在维持种群多样性方面有一定优势。
全局寻优/局部收敛平衡;邻域结构;多样性度量方式;种群多样性
在进化算法[1]研究中,全局寻优/局部收敛平衡是一个重要因素,全局寻优与种群个体的分布有较大关系。进化算法的主要问题就是存在过早收敛[2]。过早收敛的起因就是全局寻优/局部收敛平衡问(Exploration/Exploitation Balance,EEB)[3]。生物学的多样性往往与种群个体的外在特征有关,即表现型多样性,遗传算法则更多从基因型多样性来讨论多样性特征。
关于元胞遗传算法种群多样性的研究中,Alba[4]等人运用算术交叉,均匀变异并提出了一种新方法,处理具有元胞遗传算法的连续搜索空间来解决实际编码问题,并在此基础上采用非均匀变异的方法在初始空间进行均匀搜索,采用适应度高的个体代替当前个体的精英替代策略。申元霞[5]等人提出一种新型保持群体多样性的遗传算法,并从种群的熵和个体基因座的多样性来进化种群的多样性。李军华[6]等人提出一种对遗传算法多样性的检测方法,通过计算连接种群个体的连接矩阵的熵来反映种群的多样性。鲁宇明[7]等人提出了一种具有演化规则的元胞遗传算法,并采取算法元胞演化选取规则,比较了元胞遗传算法和遗传算法对多样性的维持能力。因此,元胞遗传算法可以降低高适应度个体的基因传播速度,在一定程度上保持种群多样性,改善遗传性能具有较大的优势。
1 元胞遗传算法多样性分析
1.1 元胞遗传算法原理
元胞遗传算法种群多样性的研究正是基于元胞自动机多变的演化规则,元胞空间能在复杂规则下情况下寻找函数进化过程的寻优[8]和收敛。其基本操作如图1所示。不同于标准的遗传算法,元胞遗传算法中群体的个体分布在两维网格中,每个个体分别占据网格中的一个节点,如图2所示。
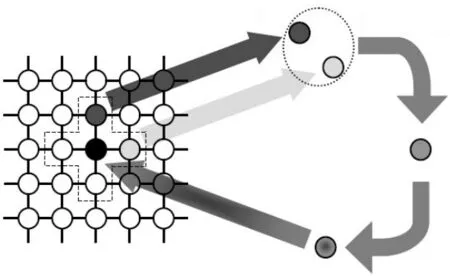
图1 元胞遗传算法图

图2 种群空间结构模型
1.2 多样性分析
元胞遗传算法以元胞自动机的主要理论为基础,交叉变异在邻域之间进行的一种遗传算法。该算法核心思想是,选择和交叉都只在一个邻域内完成,然后保留子代和父代中较优秀个体,这样就有效防止了过早收敛的发生。同时,由于邻域的重叠,保证基因不能越过邻域传递,仅可在网格之间相互传递,最优个体扩散速度减慢,这样大幅维持了种群的多样性。
2 多样性度量方式
尽管目前还没有统一的概念来定义种群多样性[9],但影响多样性主要由种群个体之间的距离[10]和种群基因频率两种因素。本文提出了遗传多样性度量方式[11](Genotypic Diversity Measures,GDM),是一种专门衡量进化过程中种群的多样性值,其能较好地控制EEB平衡。为了更好的测量GDM值,在此处提出GDM的规范化,当然一个好的GDM要能准确测量迭代过程中种群多样性值,为整个种群进化提供依据。
GDM值与种群个体之间的距离是相关的,同时也跟个体基因位出现的频率有较大关联。GDM值在评价种群多样性具有重要的参考性,表1是GDM规范条件下参数的设计。
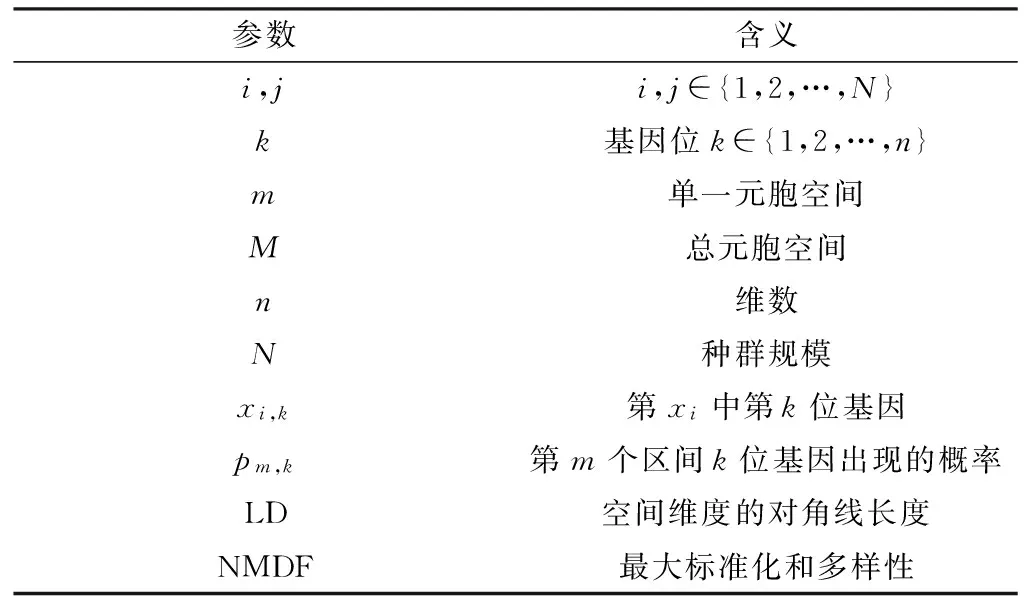
表1 GDM测量参数定义
式(1)所示
(1)
(2)
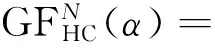
(3)
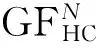
3 基于提高变异算子概率的算法
3.1 算法的定义
简单的元胞遗传算法CGA能反映元胞空间最初的个体生死状态,在进化过程中,选择和交叉算子通常正比于种群多样性,但选择与交叉算子并不能完全反映种群的多样性发展。因此,在元胞遗传算法的基础上提出了加强变异概率的模拟机制,其本质就是在二进制编码方式的基础上提升概率来促进个体适应度。为达到效果,本文提出了一种新的遗传算法(Diversity Maintaining Cellular Genetic Algorithm,DMCGA),该算法的精髓就是在选择,交叉操作后,种群会造成一部分优秀个体的损失,采取对个体进行基因变异,提高竞争压力,促进多样性的保持。
变异算子通过基因座的二进制编码进行判定,优秀个体继续保留,不适应个体则进行变异,这样就随机产生一些新个体,算法在一定周期内对全局进行变异,从而保持多样性。
3.2 DMCGA算法原理
推导:设xi,j为元胞空间种群个体,且xi,j采用基因座的二进制编码表示。初始下基因座是平衡的,也就是基因座“1”和“0”恰好各占1/2,用P(xij)=M/R公式来表示,其中M和R,分别代表种群个体xi,j“1”和“0”的总个数。在选择交叉操作后会有大量优秀个体的缺失,优秀个体的基因型特征用Φ表示,其Φ0和Φ1分别对应其两边临界点,即Φ0≤P(xij)≤Φ1,在这里取Φ0=2/3,Φ1=1。当P(xij)超出这个范围就进行变异操作,在这里用T表示,当M≫R时,则有“M-R”个数目进行变异;反之当R≫M时,则有“R-M”进行变异。
4 算法性能测试及结果分析
在测试中,选用6个测试函数对带演化规则的元胞遗传算法灾变机制下的元胞遗传算法(Celluar Genetic Algotithm With Disaster,CGAD)和本文算法DMCGA两种算法进行测试。在优化算法的全局收敛性,群体多样性以及稳定性进行分析和比较,并采用式(3)来测试新算法对GDM值保持的效果。
4.1 测试函数
F1:Shubert函数
(4)
该函数有760个局部最小值,其中18个是全局最小,其值为-186.73。
F2:Camel函数
(5)
该函数有6个局部极小值点,其中(-0.089 8,0.712 6)和(0.089 8,-0.712 6)为两个全局最小点,最小值为-1.031 628。
F3:Schaffer函数
(6)
该函数全局最优解为0,分布在(0,0)。
F4:Griewangk函数
(7)
F5:Ackley函数
(8)
该函数为一多峰函数,具有大量局部最优点,全局最小值在xi=0处取得,最小值为0。
F6:Shifted Rosenbrock函数
(9)
该函数每个变量之间都具有关联性,在xi=1时,函数取得全局最小值0。
4.2 参数设置及结果分析
测试中,将种群规模p设置为400,高维测试时,将2维设置进化最大代数为10代,在10维以上时设置为3 000代。函数优化均独立运行50次,交叉率为0.8,变异率为0.15。
统计结果如表2所示,其中,OP代表平均寻优值,CV代表平均收敛代数,GL全局收敛率,“—”表示不符合收敛条件。图3和图4是对Shubert函数和Camel函数在2维测试下的GDM值对比图。图3中DMCGA算法GDM值下降速率明显低于CGAD算法,CGAD算法在进化代数到达50代后GDM值基本就降到最低点。而从图4Camel函数的测试结果来看,虽然最初DMCGA算法对种群多样性损失较大,但迭代次数到70代左右时,发生逆转。长期进化来看,DMCGA算法对多样性的维持好于CGAD算法。
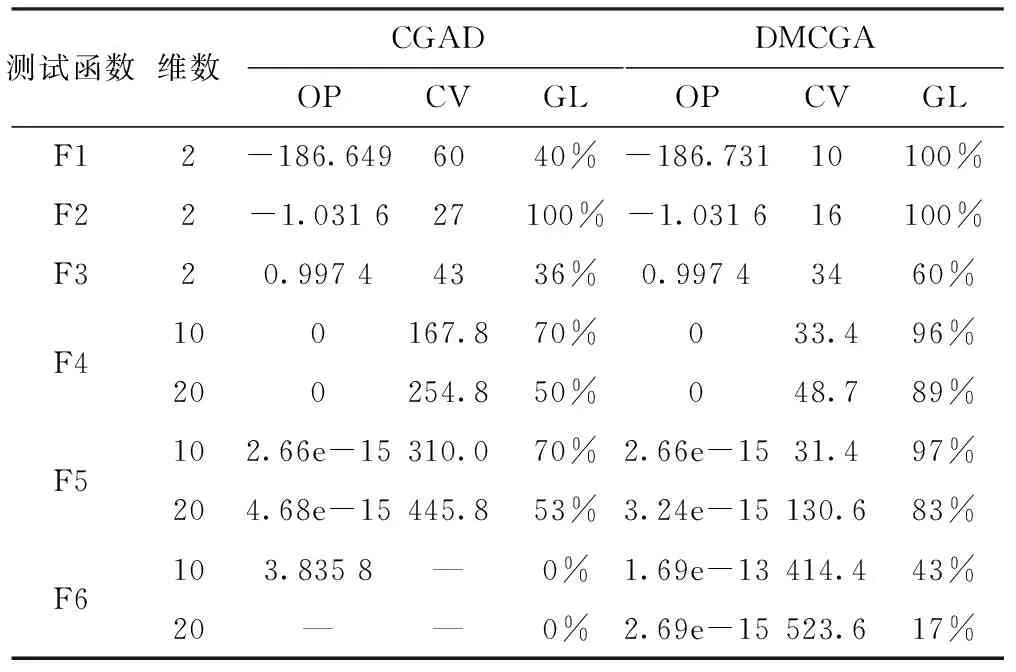
表2 DMCGA与CGAD算法测试结果对比
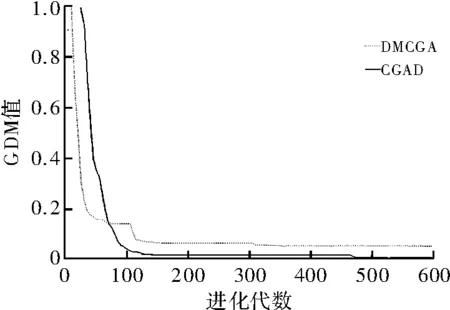
图3 Shubert函数的GDM值结果
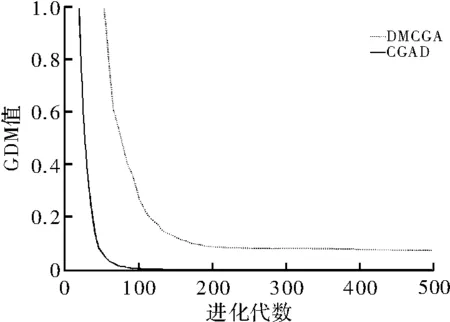
图4 Camel函数的GDM值结果
为更好地验证本文算法对高维函数的寻优能力,将本文算法对F4~F6这3个高维函数进行测试,其结果如图5~图7所示。从3个测试函数的结果来看,DMCGA算法对高维测试有较高的稳定性和收敛能力。

图5 F4函数适应值迭代曲线
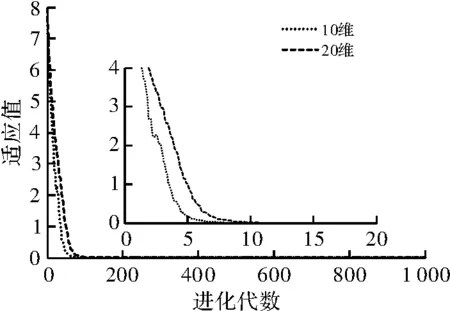
图6 F5函数适应值迭代曲线

图7 F6函数适应值迭代曲线
5 结束语
本文首先阐述了种群多样性的研究现状,提出了种群多样性的3种度量方式,并选择GF测量方式测试GDM值。最终,通过测试函数对本文算法性能进行测试,从试验结果看,DMCGA算法在函数寻优和收敛率方面取得了较好的效果,虽在高维函数测试时,仍存在一定不足,但在一定程度上可以解决函数收敛问题,提高了搜索效率。
[1] 潘正君,康立山,陈毓屏.演化计算[M].北京:清华大学出版社,1998.
[2] Eiben A E,Schippers C A.On evolutionary exploration and exploitation[J].Fundamenta Informaticae,1998,2(1-4):35-50.
[3] Wh Tlev D.Cellular genetic algorithms[C].Morgan Kaufflnann:Proceeding Softhes International Conferrenee on Genetic Algorithms,1993:658-662.
[4] Bernabe Dorronsoro,Enrique Alba.A simple cellular genetic algorithm for continuous optimization[C].IEEE Congress on Evolutionary Computation,2009.
[5] 申元霞,张翠芳.一种新型保持种群多样性的遗传算法[J].系统仿真学报,2005,17(5):1052-1057.
[6] 李军华,黎明.元胞遗传算法的收敛性分析和收敛速度估计[J].系统仿真学报,2012,25(5):874-879.
[7] 鲁宇明.一种具有演化规则的元胞遗传算法[J].电子学报,2010,38(7):1603-1607.
[8] James A Foster.Evolutionary computation[J].Nature,2001,4(2):428-436.
[9] Lieberson S.Measuring population diversity[J].America Sociol Review,1969,34(6):50-862.
[10]Olorunda O,Engelbrecht A P.Measuring exploration/exploitation in particle swarms using swarm diversity[C].In Proceeding of IEEE Congress Evolution Computer,2008:1128-1134.
[11]Guillaume Corriveau,Raynald Guilbault.Review and study of genotypic diversity measures for real-coded representations[J].IEEE Transactions On Evolutionary Computation,2012,16(5):695-709.
[12]Ursem R K.Diversity-guided evolutionary algorithms[C].In Proceeding 7thConference Parallel Problem Solving Nat.,2002,2439:462-471.
[13]Rosca J P.Entropy-driven adaptive representation.in Proc[C].Workshop Genet Program,1995,23-32.
Diversity of Cellular Genetic Algorithm
LIN Zhilong,LU Yuming
(School of Information Engineering,Nanchang Hangkong University,Nanchang 330063,China)
This paper discusses the significance of cellular genetic algorithms population diversity for exploration/exploitation balance (EEB),proposes diversity measures based on the neighborhood structure of the cellular genetic algorithm.By changing the genetic operators of the cellular genetic algorithm,the diversity of the population of the evolutionary process is maintained.The algorithm is to embed grid population space into the cellular space to simulate genetic operation between neighboring individuals.The algorithm not only improves the exploration/exploitation search ability,but it also has certain advantages in terms of maintaining the diversity of the population.
exploration/exploitation balance;neighborhood structure;genotypic diversity measures;population diversity
2014- 09- 01
江西省自然科学基金资助项目(20114BAB201046)
林志龙(1989—),男,硕士研究生。研究方向:智能优化算法。E-mail:291587960@qq.com
10.16180/j.cnki.issn1007-7820.2015.04.003
TP
A

