组合半盲均衡算法及其在半盲均衡中的应用

薛海伟,冯大政,李 进

(西安电子科技大学 雷达信号处理国防科技重点实验室,陕西 西安 710071)

组合半盲均衡算法及其在半盲均衡中的应用

薛海伟,冯大政,李 进

(西安电子科技大学 雷达信号处理国防科技重点实验室,陕西 西安 710071)

针对传输正交幅度调制信号的多输入多输出卷积通信系统中的码间干扰和共信道干扰问题,利用软决策算法的选择性以及QAM信号星座图的几何特征,提出一种组合的半盲均衡算法。该算法不仅克服了传统恒模算法,多模算法在稳态下的误调问题,而且避免了SDD算法在高阶QAM系统中运算量急剧增加的问题。采用梯度牛顿法优化CSBEA算法代价函数,与常用的梯度类算法相比,其具有收敛速度快,稳态性能好的特点。通过仿真实验证明了所提算法的有效性。

软决策算法;梯度牛顿算法;收敛速度;稳态性能

随着通信技术的发展,高数据率传输的需求日益增大。MIMO通信系统能够有效地利用频谱资源,提高传输效率[1],受到人们日益广泛的关注。然而由于空间的多径传播以及共信道问题造成的码间干扰和信号间干扰使得接收信号严重失真[2-3],导致通信质量下降甚至不可用。均衡技术是一种有效补偿由于MIMO通信系统的信道扭曲造成的信号失真的方法。因此,在通信领域,人们对高效的均衡技术有着迫切的需求。

传统的基于训练序列的均衡算法[4],由于训练序列的使用,该类算法计算简单,均衡性能较好,但其占用了较大的频谱资源[5],导致系统有效传输速率严重下降。盲均衡算法[6-7]无需训练序列,最大程度地利用了频谱资源,然而这些优点是以计算复杂度增加和均衡性能损失为代价的[8]。半盲算法[9-11]首先利用尽量少的训练样本得到一个较好的均衡器初始权值,然后用一些盲均衡算法得到最优均衡器。该方法既部分解决了基于训练序列类算法频谱利用率偏低的问题,又避免了盲均衡算法计算复杂度高,均衡精度较低的缺点。

半盲均衡算法是一种对盲均衡算法和基于训练序列算法优缺点进行折中的方法,有较大的实用价值。本文提出了一种针对传输QAM信号系统的半盲均衡算法,该算法充分利用了QAM信号星座图的几何特征构造代价函数,理论分析了其有效减少了计算量,且避免了其他算法存在的稳态下的误调问题。另外,梯度牛顿法的应用,有效利用了样本信息,加快了算法收敛速度。本文所述的半盲均衡算法与其他半盲均衡算法相同,与盲均衡算法相比,是以牺牲本分带宽效率为代价而提高了均衡性能,相反对比基于训练序列的算法,是以牺牲部分均衡性能来提高带宽效率的。

1 系统模型

考虑传输QAM信号的多输入多输出通信系统的均衡问题。如图1 所示M个输入信号sm(k)(m=1,2,…,M)经卷积信道hnm(k)(n=1,…,N;m=1,…,M)被N个天线接收,接收信号为

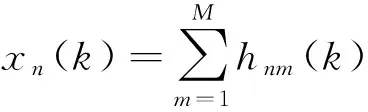
hnm(l)sm(k-l)+en(k),n=1,2,…,N

(1)

图1 MIMO系统混合及均衡模型

其中,⊗表示数字线性卷积运算。Lnm是信道hnm的阶数,en(k)是接收的高斯白噪声,sm(k)从4Z2-QAM信号中取值,即

(2)

x(k)=Hs(k)+e(k)

(3)

其中

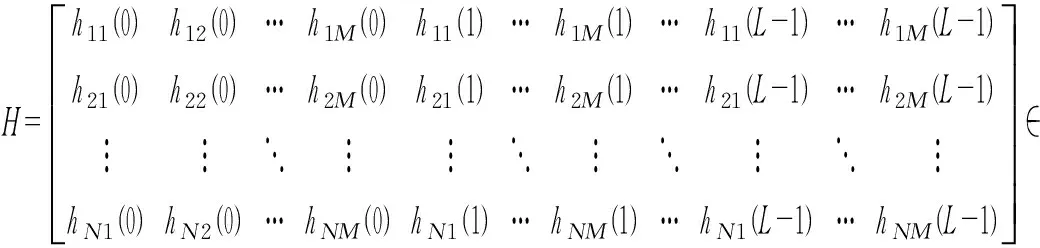
(4)

接收信号经过均衡器,输出y(k),其可表示为

2 半盲均衡器初值计算方法

由于盲均衡算法存在局部收敛和收敛速度较慢的问题,半盲算法利用尽量少的训练序列得到一个较好的初值,这样既没有牺牲过大的频谱效率,又避免了非凸代价函数的局部收敛问题,并且加快了算法的收敛速度。

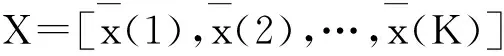
(6)

用样本均值代替整体平均则式(6)可改写为

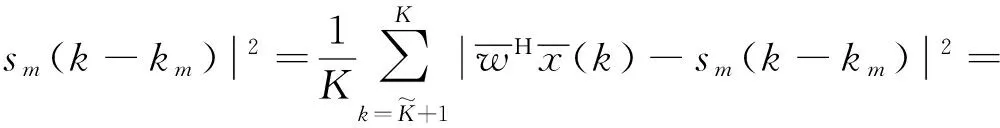
(7)

其中,“*”为取矩阵、向量或标量的共轭。对式(7)进行求导,且令导数等于0,则得到均衡器初值的估计为

(8)

3 组合半盲均衡算法(CSBEA)

盲均衡算法中一大类是借助传输信号的某种性质恢复信号的。尤其是对于传输QAM信号的系统而言,由于QAM具有很多良好的性质,依靠恢复其某种性质而达到补偿信号失真的目的,不仅简单且性能较好。现有的盲均衡算法中,恒模算法和多模算法便是以传输信号的模值特性补偿信号失真,软决策算法以其有限字符性补偿信号失真。恒模算法和多模算法虽然计算简单,但存在稳态下误调的问题[12],会导致均衡性能下降。软决策算法虽不存在误调问题,但随着QAM信号阶数的增加,其计算量会急剧增加。本文提出一种组合的半盲均衡算法,该方法利用软决策算法的选择性以及QAM的几何特性构造代价函数,其既可以避免稳态下误调的问题,又具有相对较低的运算量。

3.1 组合半盲均衡算法代价函数

各种盲(半盲)均衡算法都是恢复发射信号的某个或某几个已知特征。如图2所示,以16-QAM信号为例,经典的恒模算法恢复信号恒模特性,使得均衡后的信号趋于图中所示的虚线圆上,以均衡器输出偏离改虚心圆作为代价函数;多模算法使得恢复信号趋于图中所示的4个黑色正方形上,代价函数是以惩罚均衡器的输出偏离该4个点最小建立的。由图可知,真实的QAM信号星座点并不在如图所示的虚线圆或黑色正方形上,这就导致这两种算法在稳态条件下存在误调。软决策算法使得均衡后的信号逼近图中所示的16个小圆上,从而建立代价函数的,该方法虽然使得均衡后的信号逼近真实的QAM信号星座点,避免了前两种算法的误调问题,但是其决策项和QAM信号的星座点数一样多,将导致运算量急剧增加。为避免这些算法的缺点,文中综合利用QAM信号的星座点结构信息,以及软决策算法的选择性,使得均衡后的信号逼近图中所示的空心小圆或实心小圆上,这样决策项只有两项,这样既大幅度减少了运算量,又使得均衡信号逼近了真实的QAM星座点,避免了算法的误调。

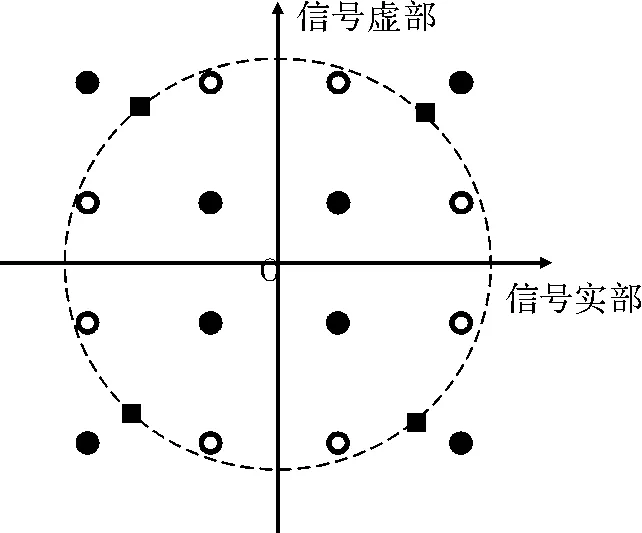
图2 恒模算法、多模算法、软决策算法及组合均衡算法示意图

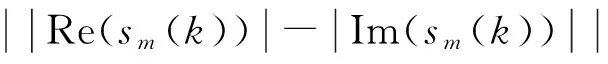
(9)

由于均衡器的输出信号y(k)是传输信号的估计,因此其也应该近似满足式(9)的关系。则文中根据软决策算法的选择性及式(9),可有代价函数

(10)

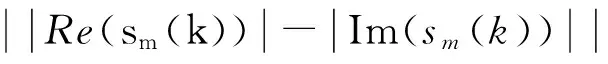
由该代价函数可知,文中所提算法具有以下优势:(1)精确利用了星座图信息和软决策算法的良好的选择性,使得均衡器输出信号y(k)不存在恒模算法,多模算法在高阶QAM系统下的稳态误调问题;(2)该方法与传统SDD算法相比,其高斯混合项大幅减少,因此计算量相比SDD算法也有大幅减少。以4Z2-QAM为例,SDD算法对于每个输出y(k)需4Z2次复数乘法和4Z2次指数运算,而文中所提的组合算法仅需Z次复数乘法和Z次指数运算。

3.2 梯度牛顿法在组合半盲均衡算法应用

传统的梯度类优化算法,虽然简单,便于操作,且运算量较小,其单次迭代的运算量约为O(L″),但其收敛速度缓慢。因此,改用梯度牛顿算法对代价函数进行优化,该方法具有近似二阶的收敛速度,其代价是运算量相对较大,其单次迭代运算量约为O(L″2)。

对式(10)进行微分得

(11)

用瞬时梯度代替代价函数的当前梯度,即

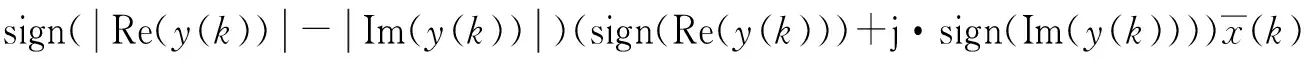
(12)

且用样本的相关函数修正当前梯度,得到基于梯度牛顿法(GN)的CSBEA(GN+CSBEA)的迭代公式为

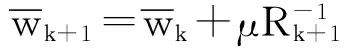
(13)

其中,R-1是样本相关矩阵的逆矩阵,由矩阵求逆引理可得其更新式为

(14)

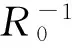
4 仿真结果

文中用稳态性能和收敛速度来评价提出算法的性能。稳态性能和收敛速度均用信道最大扭曲(CMD)来衡量。如果均衡器和信道的综合响应定义为

(15)

(16)

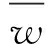
(17)

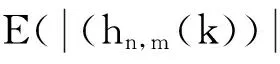
图3为4种算法的平均最大信道扭曲随信噪比的变化曲线。由图可知,所提半盲算法的性能,在相同条件下明显优于SG-CMA+SDD算法的性能,其主要原因是本算法精确利用了QAM信号的星座图信息,避免了SG-CMA+SDD算法使用恒模算法带来的误调问题及其硬判决所带来的误差;虽然该算法性能并未达到最优的MMSE算法性能,但本算法仅用了较少的训练序列,相对于MMSE算法,大幅提高了系统的有效信息传输率,且性能也明显优于只用相同训练序列的LSCE算法。

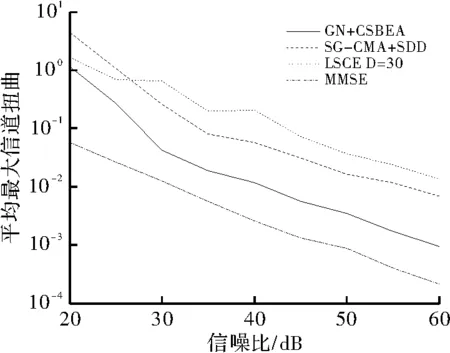
图3 平均最大信道扭曲随信噪比变化曲线

图4为4种算法的收敛曲线。文中重点比较了两种半盲算法,由图可知,本算法初始收敛速度较快,且约在迭代1 000次后趋于稳定,而SG-CMA+SDD算法收敛缓慢。而文中提出算法收敛快的原因主要在于,其利用了样本的相关矩阵校正代价函数的梯度,属于梯度牛顿类算法,具有近似二阶的收敛速度,而SG-CMA+SDD属于梯度类算法,其是一阶收敛的。在实际应用中,该算法可利用较少的样本达到较高的均衡性能,使得实用性更强。此外,由最终稳态下的平均最大信道扭曲也可以证明所提算法良好的均衡性能。

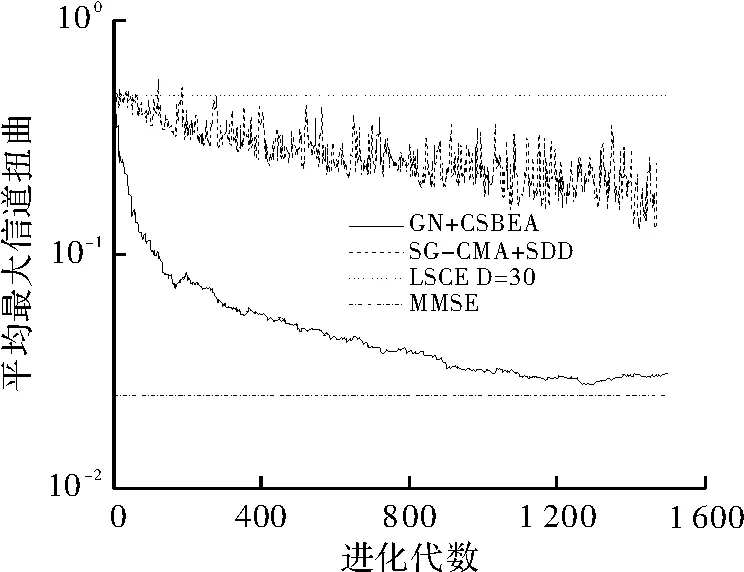
图4 平均最大信道扭曲随迭代次数变化曲线

5 结束语

针对传输正交幅度调制信号的输入多输出卷积通信系统中的码间干扰和共信道干扰问题,提出一种组合的半盲均衡算法。该算法精确利用了QAM信号的星座图的几何特征,避免了类似传统恒模算法和多模算稳态下的误调问题及SDD算法在高阶QAM系统中运算量急剧增加的问题。在代价函数优化过程中,梯度牛顿算法以运算量的增加为代价,加快了算法收敛速度,并且提高了算法的稳态性能。使得该算法可用较少的样本达到良好的均衡性能,使其实用性增强。

[1]FoschiniGJ.Layeredspace-timearchitectureforwirelesscommunicationinafadingenvironmentwhenusingmulti-elementantennas[J].BellLabsTechnologyJournal,1996,1(2):41-59.

[2]GodardDN.Self-Recoveringequalizationandcarriertrackingintwo-dimensionaldatacommunicationssystems[J].IEEETransactionsonCommunications,1980,28(11):1867-1875.

[3]TreichlerJR,AgeeBG.Anewapproachtomultipathcorrectionofconstantmodulussignals[J].IEEETransactionsonAcoustics,SpeechandSignalProcessing,1983,31(2):459-472.

[4]ZhuX,MurchRD.Layeredspace-frequencyequalizationinasingle-carrierMIMOsystemforfrequency-selectivechannels[J].IEEETransactionsonWirelessCommunications,2004,3(3):701-708.

[5]KayS.Fundamentalsofstatisticalsignalprocessing:estimationtheory[M].EnglewoodCliffs,NJ:Prentice-Hall,1993.

[6] 杨源,李明阳,王徐华.一种改进的稀疏多径信道均衡方法[J].西安电子科技大学学报:自然科学版,2014,41(1):158-163.

[7]NaftaA,JohannissonP,ShtaifM.Blindequalizationinopticalcommunicationsusingindependentcomponentanalysis[J].JournalofLightwaveTechnology,2013,31(12):2043-2049.

[8]ChenS,YaoW,HanzoL.Semi-blindadaptivespatialequalizationforMIMOsystemswithhigh-orderQAMsignalling[J].IEEETransactionsonWirelessCommunications,2008,7(11):4486-449.

[9]YuJL,ZhangB,ChenPT.Blindandsemi-blindchannelestimationwithfastconvergenceforMIMO-OFDMsystems[J].SignalProcessing,2014,95(2):1-9.

[10]GogoiP,SarmaKK.Kalmanfilterandsemi-blindtechnique-basedchannelestimationforcodedSTBCmulti-antennaset-upsinfadedwirelesschannels[J].InternationalJournalofInformationandCommunicationTechnology,2014,6(1):86-108.

[11]BhalaniJK,ChauhanD,KostaYP,etal.Nearoptimalperformancejointsemi-blindchannelestimationanddatadetectiontechniquesforAlamouticodedsingle-carrier(SC)MIMOcommunicationsystems[J].PhysicalCommunication,2013(8):31-37.

[12]TreichlerJR,AgeeBG.Anewapproachtomultipathcorrectionofconstantmodulussignals[J].IEEETransactionsonAcoustics,SpeechandSignalProcessing,1983,31(2):459-472.

Study of the Fast Semi-Blind Equalization Algorithm for the QAM Communication System

XUE Haiwei,FENG Dazheng,LI Jin

(National Key Lab of Radar Signal Processing,Xidian University,Xi’an 710071,China)

Due to the inter-symbol interference(ISI) and co-channel interference(CCI) of the MIMO convolutional communication system driven by QAM signals,a combined semi-blind equalization algorithm (CSBEA) is proposed by utilizing the selectivity of the soft decision directed(SDD) algorithm and the geometric properties of constellation of QAM signals.This algorithm overcomes the maladjustment in the steady state of constant modulus algorithm and multimodulus algorithm and avoids the problems of a rapidly increased computational load of SDD algorithm of high order QAM systems.Furthermore,the gradient Newton method is adopted to optimize the cost function of the proposed CSBEA,which brings about a faster convergence speed and a better steady state performance than that of gradient-type algorithms.Finally,several experiments are provided to illustrate the effectiveness of the proposed method.

soft decision directed algorithm;gradient Newton method;convergence speed;steady state performance

2014- 09- 02

国家自然科学基金资助项目(61271293)

薛海伟(1985—),男,博士研究生。研究方向:干涉SAR数据处理,SAR成像,盲信号处理。E-mail:xuehw001@gmail.com。冯大政(1959—),男,教授,博士生导师。研究方向:雷达成像,阵列信号处理,盲信号处理,神经网络等。李进(1985—),男,博士研究生。研究方向:盲信号处理。

10.16180/j.cnki.issn1007-7820.2015.04.002

TP301.6

A

1007-7820(2015)04-004-05