平面杆件体系几何组成分析方法的探讨

阳令明　肖穗花



平面杆件体系几何组成分析方法的探讨

阳令明1肖穗花2

（1.湖南科技学院 土木与环境工程学院，湖南 永州 425199；2.邵阳市洞口县东边中学，湖南 邵阳 422000）

平面杆件体系几何组成分析是结构力学教学的重点与难点之一，具有概念抽象、技巧性强、结构体系多变的特点，在结构力学多年的教学体会与反思的基础上，分析和总结了自由度W=0的平面结构如何应用几何不变体系的组成规则及零载法进行结构分析的思路及技巧，并辅以例题具体说明，对学生掌握好本知识点内容具有指导意义。

结构力学；平面杆件体系；几何组成分析；方法

结构力学是土木工程专业一门重要的专业基础课，它既是前续《理论力学》、《材料力学》课程的深化与延续，也是后续《混凝土结构设计》、《钢结构》等专业课程的基础。平面体系几何组成分析是结构进行力学分析与计算的基础，它的目的是确定体系的几何组成属性，判断其能否作为结构，也通过了解体系的各个部分的相互关系，改善和提高结构的受力性能，以及确定结构的计算方法和计算顺序。由于这一章的内容概念性及技巧性均较强，结构体系又千变万化，初学者常常会感到无从下手，部分教学工作者对于如何掌握这部分内容已展开了研究和探讨，主要集中在特殊或典型问题的总结[1~5]。本文基于几何不变体系的组成规则及零载法的分析，探讨对于自由度W=0的平面体系进行几何组成分析的解题思路及技巧，帮助学生理解和掌握该知识点的内容。

1　几何组成的基本规则

结构力学教材中[6]，自由度W=0的平面几何不变体系，其几何组成基本规则有三种方式：一点一刚片通过两不共线链杆连接（二元体规则），两刚片通过三不共点（不全平行）链杆连接或不共线一铰一链杆连接（两刚片规则），以及三刚片通过不共线三铰连接（三刚片规则）。采用几何不变体系的组成规则解题，其关键是刚片的选择，约束的判断及组成规则的灵活应用，即如何选择刚片，如何利用规则分析判断。

1.1 刚片的选择

刚片是指不论其具体形状如何，本身为几何形状不变者，可以是链杆（直杆、曲杆、折杆），基础或基础的扩大部分，以及已确定的几何不变部分。解题时应首先判断基础是否作为刚片，当支杆S=3时，可把基础去掉，只分析体系本身的几何属性，当支杆数S＞3时，应把基础当成一个刚片。其次，根据体系组成两刚片规则，一个刚片与另一刚片应有三个联系，按照三刚片规则，刚片两两间应有两个联系，即一个刚片和外界应有四个联系，这样我们可以试着选择一个刚片，根据该刚片与外界的联系来选择其他的刚片[5]。最后，应用几何组成规则进行分析判断。

1.1.1去掉基础刚片

如图1所示的体系[6]，体系与基础有三个联系，由两刚片规则，可去掉基础这一刚片，只分析体系内部几何关系，如果内部几何关系为几何不变部分，则结构是几何不变的，同时利用二元体规则，依次去掉ACD、BJK、CDE、JIK二元体，留下GEDKI结构体系，体系有两个铰结三角形，任选GEF为第一刚片，它与外界有ED、FK及铰G（或GH、GI）四个联系，判断出DK、GHI（或HI）分别为第二或第三刚片，形成实铰O1、O2、O3，三铰不共线，GEDKI结构体系是几何不变的，故整个体系是几何不变体系且无多余约束。

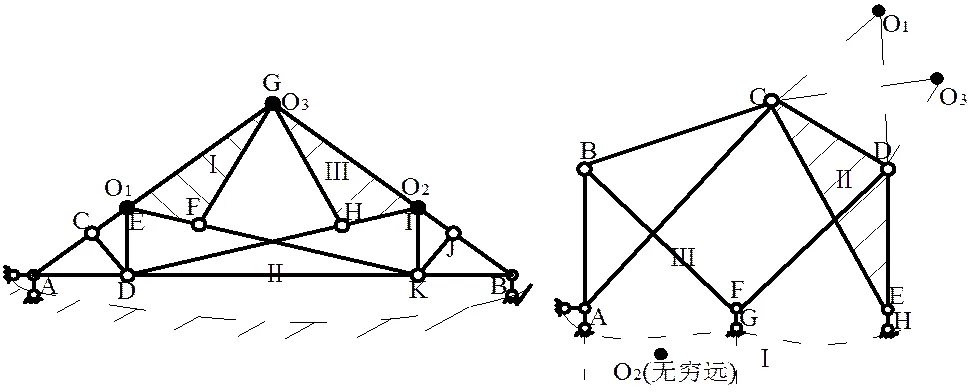
图1 图2

1.1.2 基础作为第一刚片

如图2所示的体系[6]，体系与基础有四个联系，基础应作为第一刚片，其伸出的四个联系为AB、AC、HE、GF，判断出CDE、BF为第二或第三刚片，形成虚铰O1、O2、O3，三铰不共线，几何不变体系且无多余约束。

1.1.3扩大后的刚片

如图3所示的体系[6]，体系与基础有三个联系，可只分析体系内部几何关系，此时宜首选铰结三角形作为第一刚片， CDB、AHG为铰结三角形，DEB、AFG分别为CDB、AHG上的二元体，则选择AFH或BEC作为第一刚片，它与外界有EF、BH、AC三个联系，判断BEC或AFH为第二刚片，根据两刚片规则，为几何不变体系且无多余约束。

图3 　 图4

1.1.4等效替换后的刚片

如图4所示的体系[6]，体系与基础有四个联系，基础作为第一刚片，其伸出的联系为A、B、C、D四个支杆，考虑到刚片的各种形式可相互转换，分析时把BC、AD、AB、CD四根折杆看成如图虚线所示的四根直链杆，判断出BC与AD或AB与CD为第二或三刚片，形成虚铰O1、O2、O3，三铰不共线，几何不变体系且无多余约束。

1.2 约束的替换

由于体系各杆件之间或体系与基础之间是通过约束来实现相互的制约作用，它只与约束的数量及布置有关，与形式无关，因此约束的各种形式（链杆、支杆、铰结点、刚结点）可互相等效替换。比如把链杆中的曲杆或折杆、基础或基础中的部分支杆替换成直链杆，或已确定的几何不变部分替换成基础，或把两个链杆约束替换成一个延长线上的虚铰结点等。如果运用几何不变体系的组成规则不能直接进行判断时，可考虑约束的等效替换。

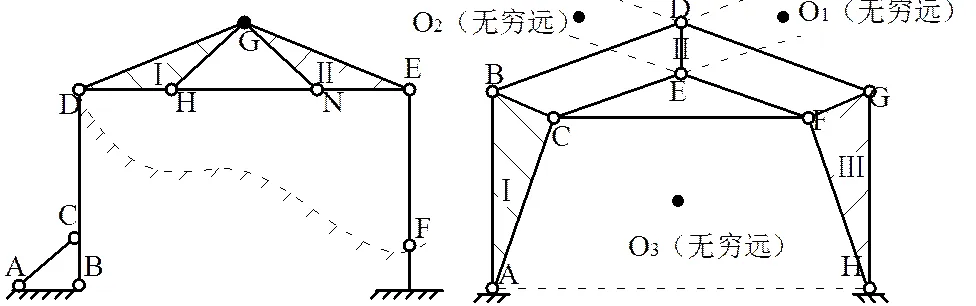
图5 图6

如图5所示的体系，DBAC及F杆是基础上的几何不变部分，分析时可等效替换成基础，如虚线所示。结构DEG与基础有三个联系，可只分析体系的内部几何关系，选择铰结三角形DHG或GNE为第一刚片，它与外界有G铰结点、HN链杆三个联系，则GNE或DHG为第二刚片，根据两刚片规则，结构为几何不变且无多余约束。

如图6所示的体系[6]，结构ABDGH与基础通过铰A和铰H联系，分析时如果把地基作为第一刚片，则BC、FG为第二或第三刚片，无法利用几何组成规则进行判定，如果把基础替换成直链杆AH，如虚线所示，便可只分析体系内部几何关系，选择铰结三角形ABC为第一刚片，它与外界有BD、CE、CF、AH四个联系，判断出DE、HGF为第二或第三刚片，形成虚铰O1、O2、O3，三铰均在无穷远处，几何瞬变体系。

2　零载法

在一些复杂的结构体系中，采用几何不变体系的组成规则无法判断时，可采用零载法来判定。根据静定结构的性质，在无荷载作用的情况下，静定结构中不会产生反力和内力，即静定结构在零荷载作用下，各未知力的唯一解答只能是零。

应用零载法进行结构分析时，一般先判断出零杆，对无法直接判断的杆件先假设其内力值或结构支反力为N，再求出其他所有杆件的内力值，最后得出该内力值N的唯一解答为零，从而判定为几何不变体系，否则为几何可变体系，其求解过程就是受力分析过程。

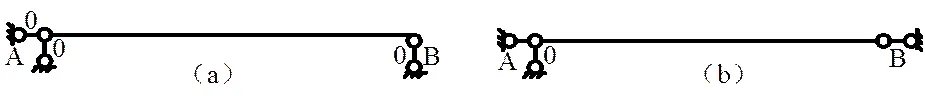
图 7

2.1 假设支反力为N

如图8所示的结构[6]，采用几何组成规则判断时感觉无从下手，此时考虑用零载法，设A的支反力为，由，可知，取隔离体AFE和BFG，由及，可知，即，故结构是几何不变的。

图8

2.2 假设非零杆内力为N

如图9所示的桁架结构[6]，结构体系复杂，考虑用零载法，图中虚线部分是零杆。

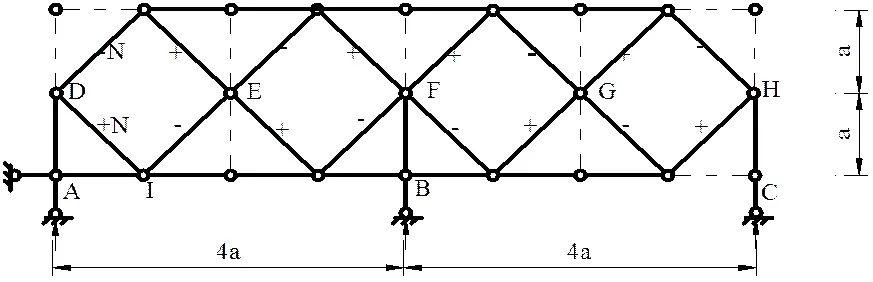
图9

3　结语

平面体系的几何组成分析是结构力学的基础，也是重点。本文主要针对平面杆系结构几何组成分析时存在的困难，根据自己教学过程中的体会和反思，论述了平面体系几何分析的一般方法，对刚片的选取，约束的替换，以及零载法的解题思路及技巧等提出了自己的一些看法，从学生的反映来看，该方法技巧易于掌握，适用性较强。

[1]张琳楠,徐春晖,秦太验.平面体系机动分析的一般方法[J].力学与实践,2014,36(6):738-741.

[2]孙丽莹.平面体系几何组成分析广义三角形规则新思路[J].力学与实践,2013,35(6):84-87.

[3]樊友景,樊大为.几何构造分析中的等效变换[J].力学与实践,2012,34(2):77-78.

[4]邱秀梅,戴景军,孙建武.平面体系几何组成分析的方法技巧[J].力学与实践,2009,31(2):80-81.

[5]李秀梅,韦斌凝,陈建芳.基于平面杆系几何组成规则的刚片选取[J].广西大学学报(自然科学版)增刊,2004,29:125-127.

[6]朱伯钦,周竞欧,许哲明.结构力学（第三版）[M].上海:同济大学出版社,2014,2:18-38.

（责任编校：何俊华）

2015－06－24

阳令明（1984－），男，湖南邵阳人，工程师，硕士，主要从事力学教学与研究。

G420，O342

A

1673-2219（2015）10-0067-02