基于RBF-ARX模型的改进多变量预测控制及应用

曾小勇，彭辉，吴军



基于RBF-ARX模型的改进多变量预测控制及应用

曾小勇1, 2，彭辉1，吴军1

(1. 中南大学信息科学与工程学院，湖南长沙，410083；2. 长沙理工大学电气与信息工程学院，湖南长沙，410076)

针对一类工作点时变的光滑非线性多变量被控对象，采用离线辨识的RBF-ARX模型描述系统的全局非线性动态特性，并在此基础上提出一种具有自适应微分作用的非线性模型预测控制方法。该方法将整个预测时域内模型输出和期望输出的偏差变化率考虑到优化目标中，利用与偏差变化率有关的函数动态修改该优化项的权重,从而能在保证控制器稳态性能的情况下有效地改善系统的动态性能。最后利用该方法对四旋翼飞行器实验装置进行了实际的姿态控制，控制效果验证该方法的有效性。

RBF-ARX模型；非线性模型预测控制；四旋翼飞行器

非线性模型预测控制(NMPC)由于突破了传统控制策略的束缚，能有效处理工业过程中普遍存在的非线性现象和系统约束，而受到控制工程界和理论界的广泛关注[1−2]。NMPC是一种基于预测模型的优化控制算法，对于工业过程中存在的各类非线性对象，采用线性化建模方法[3−4]难以完整描述工业现场大量存在的强非线性特性；而直接非线性建模[5−8]通常都包含有高阶的在线非线性优化问题，对于实时性要求较高的实际工业对象很难取得满意的控制效果。因此，近年来大量的研究和应用都侧重于利用组合预测模 型[9−14]。该类方法将被控对象分解为非线性和线性空间，使整个系统具有局部线性全局非线性的特性，便于实现离线设计，在线综合的预测控制算法，可大幅降低在线计算量，有利于在实际工业现场的应用。PID控制器由于其简单的反馈控制结构仍广泛应用于工业现场中，将PID控制思想与预测控制算法相结合可进一步提高预测控制器的性能。文献[15−16]提出了一种比例积分型一步预测控制方法，并通过算例仿真结果说明了该方法的优越性，但由于未涉及到对象的建模，忽略了建模误差对预测控制结果的影响，这在实际工业控制中将影响控制器的性能。本文作者针对一类工作点时变的光滑非线性多变量被控对象，采用状态相依自回归(SD-ARX)模型描述系统的非线性状态特征，用高斯径向基函数(RBF)神经网络近似SD-ARX模型的函数型系数，在递推得出以状态信号量引导的多步状态空间预测模型的基础上，结合传统的多步模型预测控制策略，将整个预测时域内模型输出和期望输出的偏差变化率考虑到优化目标中，相当于对偏差的微分也进行优化控制。为了减少建模误差对控制器稳态误差的影响，在优化过程中根据偏差变化率的信息动态调整其权重系数，从而能在保证控制器稳态性能不变的情况下有效地抑制由于系统惯性和输入时滞所带来的超调，缩短调节时间，改善系统的动态性能。最后，利用该方法对四输入三输出的四旋翼飞行器实验装置的飞行姿态进行实际控制，控制结果验证了该方法的有效性。

1 非线性对象模型

1.1 非线性对象描述

对于工业过程中大量存在的非线性现象，建模的主要问题就是构建如下一个函数：

其中：()为输出；()为输入；a和b分别为输出输入阶次；()为白噪声序列。

其中：和=dim((−1))分别为RBF网络的节点数和中心维数；和为RBF网络描述的状态相依ARX模型函数系数；和分别为RBF网络的中心和宽度；，和，分别为RBF网络的阀值和线性权重；为向量的2范数；为白噪声序列。利用Peng等[17]提出的结构化非线性参数优化方法(SNPOM)离线估计模型参数。在实时控制中，模型(3)通过状态信号量的更新来实时反映被控对象的动态特性。状态信号量通常是选取最能反映被控对象动态特性的动态变量，所以它可能是与输入或输出有直接或间接的关系，在某些时候也可能就是输入与输出的组合或是其他相关信号量。当该状态量为固定值时，状态相依ARX模型就可以衍变成为一个ARX模型，因为系统状态信号量的变化，状态相依ARX模型能随时在不同的局部子空间内进行即时平滑的转换，从而使得状态相依ARX模型具有全局有效的特性。

1.2 状态相依ARX模型的状态空间描述

将模型(3)变换成如下矩阵多项式形式：

由此可根据模型(4)可定义如下的状态变量：

(5)

根据模型(3)或模型(4)和定义的状态变量式(5)可推出对象的状态空间模型为

其中：

特别指出的是，通过状态变量式(5)的定义，当前时刻的状态()可以由过去时刻的状态、输入输出数据以及估计的状态相依ARX模型的系数计算得到，不需要再使用状态观测器估计当前时刻的状态。

1.3 递推多步状态空间预测模型

模型(3)，(4)和(6)可认为是一步预测模型，为了得到非线性对象的多步预测模型，定义如下向量：

式中：和N分别为预测时域和控制时域，且满足≥N，从N到时域内认为输入为N时刻的输入并保持不变；和()分别为时刻带模型预测输出序列和期望输出序列，通常，期望输出序列即参考轨迹为当前时刻期望值()的柔化序列：

定义系统的多步预测模型的状态空间描述为

式中：

(13)

2 改进的非线性模型预测控制

传统的非线性模型预测控制策略一般将非线性预测模型作为控制器的内模，将当前时刻的最优输入问题转化为某个有限预测时域内模型输出和期望输出的偏差最小的优化问题，同时根据模型输出和实际输出的历史偏差信息对预测模型进行反馈校正，并在下一个采样周期向前滚动优化。通常将模型预测控制的目标函数定义为

(17)

其中：，1和2为权重对角阵；()和分别为时刻优化的控制序列和控制增量序列。设置控制加权阵1和2是为了减少对被控对象过大的冲击，一般情况下，加大其权重可以提高系统的稳定性，但同时也减弱了控制作用，还可能增大系统的稳态误差，一般的做法是在系统能够稳定的情况下，应使其权重尽可能的小。

优化控制的目的是为了找到一个控制量使得被控对象的性能满足要求，调节式(17)中的权重系数和输出期望序列()可均衡控制系统的动态和稳态性能，也就是说，某个较好的控制性能指标通常是以牺牲其他性能指标为代价的。特别对于一些复杂的实际工业对象，如何在保证控制器稳态性能不变的情况下有效地抑制由于系统惯性和输入时滞所带来的超调，缩短调节时间，改善系统的动态性能显得尤为重要。根据PID的控制思想，输出偏差微分项的引入可有效改善系统的动态性能。由此，改进型模型预测控制的目标函数定义为

定义当前时刻模型预测输出序列和期望输出序列的偏差序列为

将式(21)变形为

可得到改进型的非线性模型预测控制目标函数为

(23)

式中：为偏差变化率的权重对角阵。

需要特别说明的是：

2) 由式(23)可以看出：优化的目标是期望获得一组()使得()和，之间的偏差最小，在系统的动态过程中，可理解为对期望序列的在线修正，以帮助系统提前动作，减少系统的超调量，缩短调节时间。

3) 在系统进入稳态后，如果预测模型能准确地描述系统，即对象实际输出等同于模型预测输出，系统不存在稳态偏差，即在系统进入稳态后，，式(23)等同式(17)，可见，输出偏差变化率的引入在改善系统的动态性能的同时不会影响系统的稳态性能。但由于实际系统的复杂，不可避免的存在模型失配，使得系统存在稳态偏差，此时输出偏差变化率的引入可能导致稳态偏差的加大，为了消除偏差变化率对稳态偏差的影响，可将其权重系数定义为模型预测输出序列和期望输出序列的偏差变化率的函数。在动态过程中，是与系统动态特性相关的常数，此时偏差变化率权重较大，可有效改善系统的动态性能，当系统进入稳态后，将趋向于0，偏差变化率权重也将趋向于0，从而保证偏差变化率的引入在改善系统动态性能后不影响系统的稳态偏差。

将式(10)进行如下变换，

则可将式(23)转化为标准的二次规划形式：

(25)

其中：

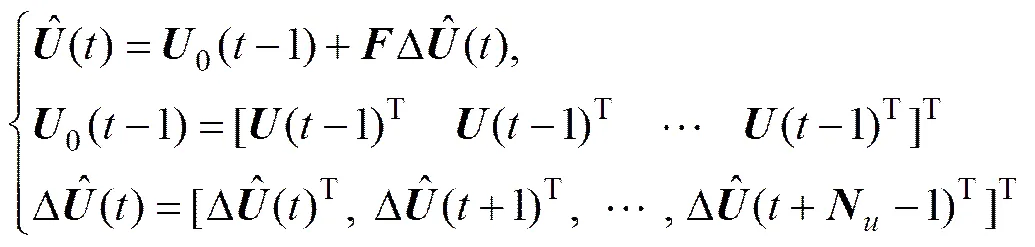
是和输入变量数有关的常数项矩阵。

式(25)的求解是一个非线性在线优化问题，可通过二次规划相关方法进行优化，当不考虑式(25)的约束条件时，可直接对输入进行求导限幅，求得输入序列为

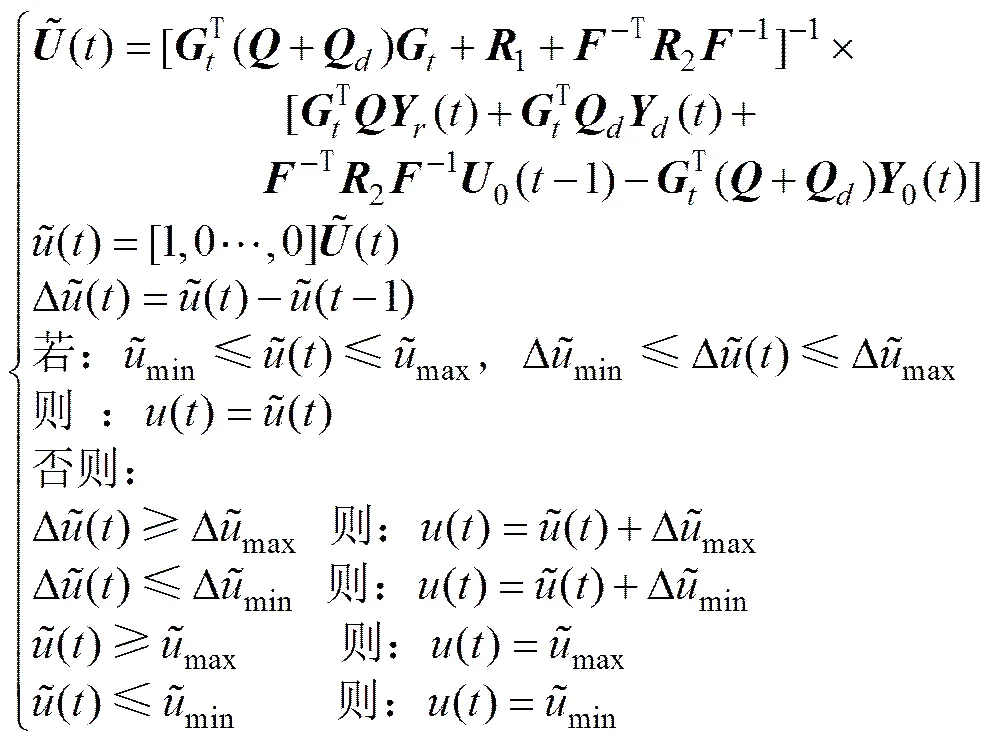
对于优化得到的输入序列，仅使用最新时刻的输入作为控制输入。

3 应用研究

3.1 对象描述

图1所示为四旋翼飞行器物理结构图。为了验证本文方法的有效性和可行性，选取实验室基于物理模型的二次型最优调节器(LQR)控制的四旋翼飞行器姿态控制实验装置(如图１所示)为被控对象，四旋翼飞行器是一个四输入三输出的非线性带耦合对象，4个输入分别是对4个螺旋桨提供动力的电机电压，约束为[−20 V，20 V]，3个输出分别为绕轴旋转的俯仰角、绕轴旋转的翻转角和绕轴旋转的巡航角。

(a) 实物图；(b) 力学坐标图

3.2 对象模型

(a) 俯仰角；(b) 翻转角；(c) 巡航角

(a) 俯仰角；(b) 翻转角；(c) 巡航角

从图2和3可以看出：状态相依ARX模型具有较好的建模效果，模型预测输出很好的拟合了实际输出，预测误差近似白噪声信号且总体在很小的范围内变动。

3.3 实时控制效果及分析

确定预测时域=30，控制时域N=10，柔化因子=0.1，线性权重对角阵为，且在每个预测时域内保持不变。为了验证改进型非线性模型预测控制方法的改进效果，在保持其他参数不变的情况下，将模型预测输出序列和期望输出序列的偏差变化率考虑到优化目标中，为了保证偏差变化率的引入在改善系统的动态性能的同时不影响稳态性能，式(18)中权重对角阵的动态调整非常关键，本文将其取为关于第1个预测时域的偏差变化率的函数，(式中：分别为3个输出偏差变化率绝对值的均值)。

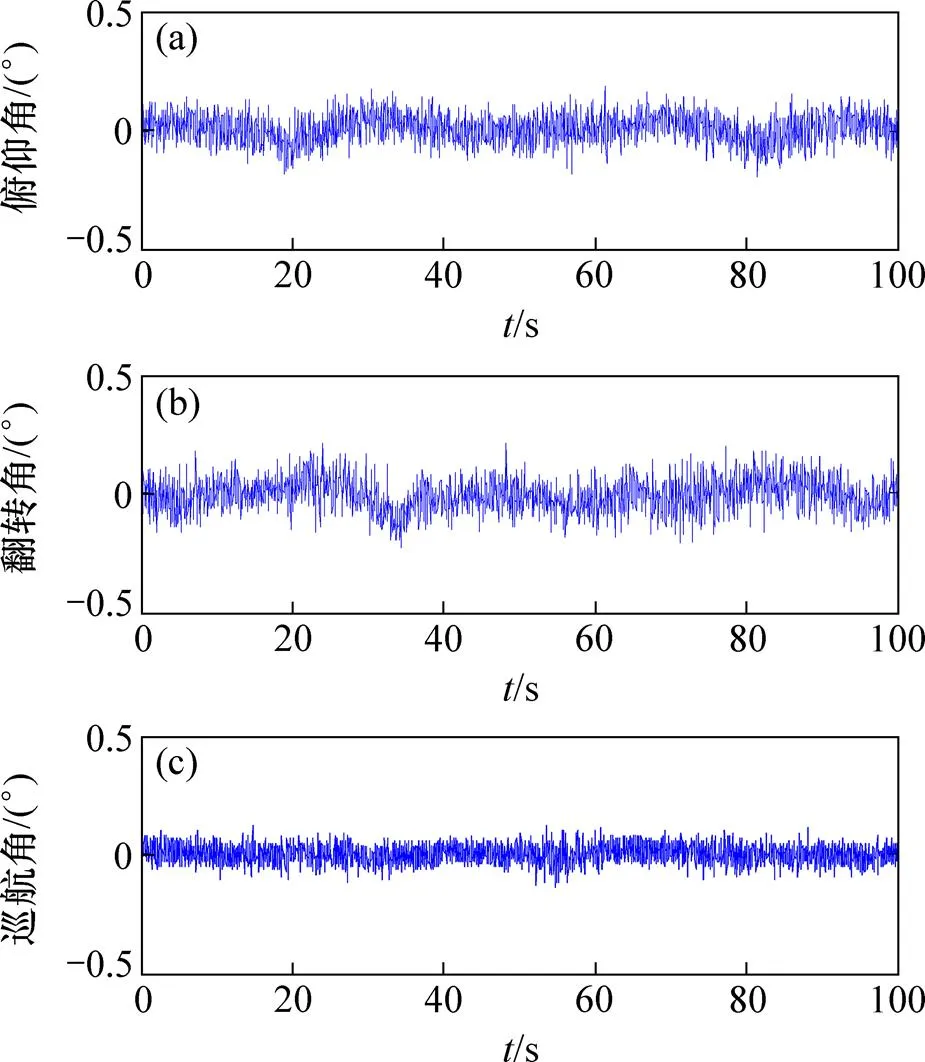
图4所示为传统非线性模型预测控制(实线)和改进型非线性模型预测控制(点线)的阶跃响应曲线。由于四旋翼飞行器状态是飞行器的水平状态，这一状态是十分敏感的，小幅的波动都将使其从这一状态滑落，这一状态的改变最能体现控制器的控制效果。由图4可知：改进的方法在减少系统超调和缩短调节时间的同时没有增加系统的稳态偏差。另外由于飞行器的巡航角具有较大的偏差变化率加权，使得其上升缓慢，但动态性能也优于传统非线性模型预测控制器。

(a) 俯仰角；(b) 翻转角；(c) 巡航角

图5所示为改进型非线性模型预测控制阶跃响应对应的输入曲线，4个输入都很好地约束在[−20 V，20 V]内。图6所示为用于动态调整偏差变化率加权的第1个预测时域内的模型输出和期望输出偏差变化率曲线。由图6可知：当系统处于动态变化过程时，偏差变化率较大，而当系统过渡到稳态时，偏差变化率趋向于0，从而保证了偏差变化率的引入在改善系统动态特性的同时不影响系统的稳态性能。

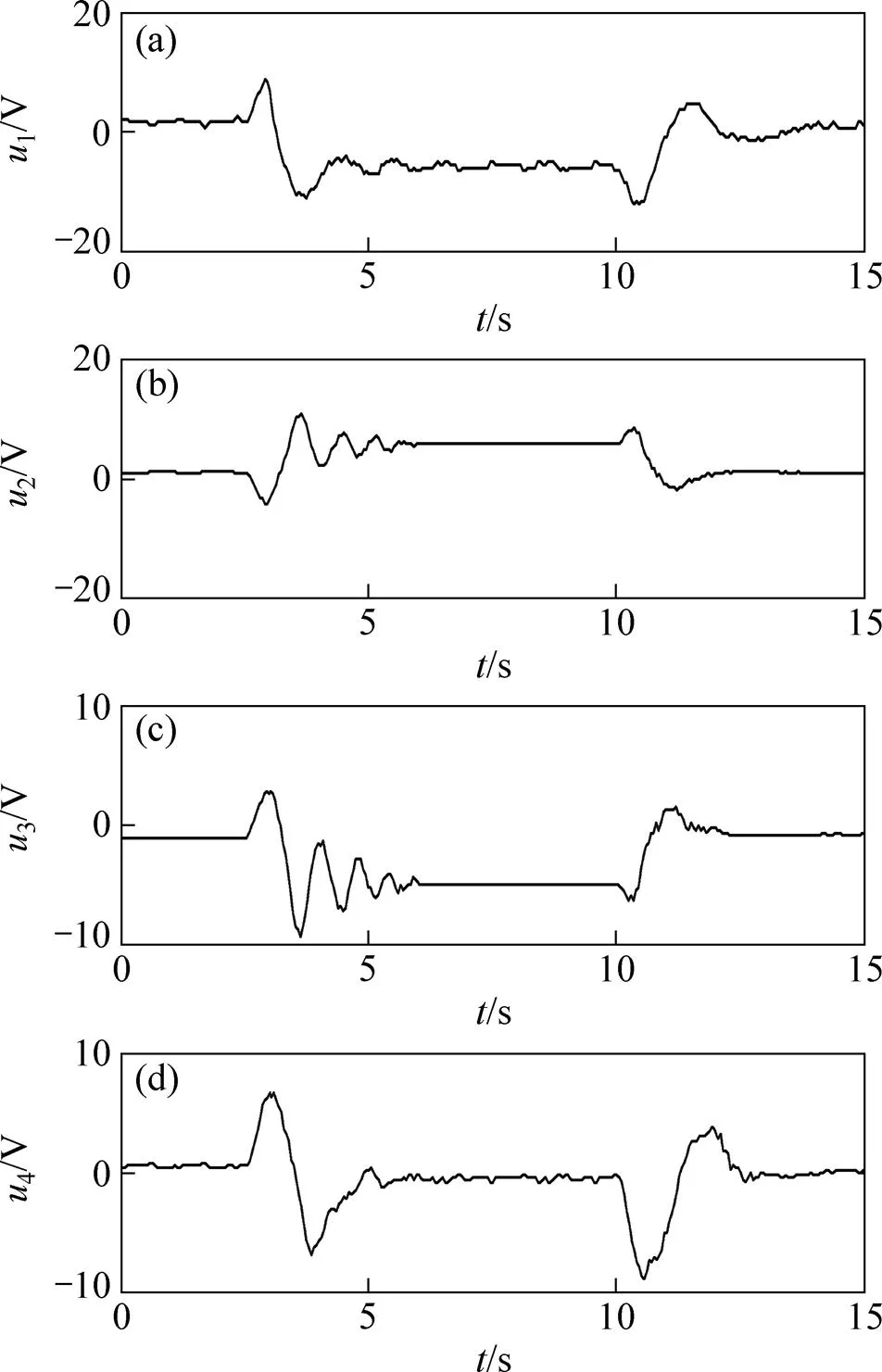
(a) Vf；(b) Vr；(c) Vl；(d) Vb

(a) 俯仰角；(b) 翻转角；(c) 巡航角

由于本文采用离线的结构化非线性参数优化方法估计模型参数，采用Ｃ语言编制程序，并在算法上尽量进行了简化，使得复杂的非线性预测控制策略得以在50 ms的控制周期内实现。

4 结论

对一类工作点时变的多变量非线性系统提出了一种改进型的非线性模型预测控制方法，该方法将模型预测输出和期望输出的偏差变化率引入到滚动优化中，同时利用与偏差变化率有关的函数动态修改该优化项的权重，使得该方法在保证系统稳态性能的情况下有效改善系统的动态性能，利用该方法对四旋翼飞行器实验装置进行实时控制，取得了比传统的非线性模型预测控制算法更好的控制效果。

[1] 席裕庚, 李德伟. 预测控制定性综合理论的基本思路和研究现状[J]. 自动化学报, 2008, 34(10): 1225−1234. XI Yugeng, LI Dewei. Fundamental philosophy and status of qualitative synthesis of model predictive control[J]. Acta Automatica Sinica, 2008, 34(10): 1225−1234.

[2] Qin S J, Badgwell T A. A survey of industrial model predictive control technology[J]. Control Engineering Practice, 2003, 5(11): 733−764.

[3] Prasad G, Swidenbank E, Hogg B W. A local model networks based multivariable long-rang predictive control strategy for thermal power plants[J]. Automatica, 1998, 34(2): 1185−1204.

[4] Giarre L, Bauso D, Falugi P, et al. LPV model identification for gain scheduling control: An application to rotating stall and surge control problem[J]. Control Engineering Practice, 2006, 14(4): 351−361.

[5] Mizuno N, Kuroda M, Okazaki T. Minimum time ship maneuvering method using neural network and nonlinear model predictive compensator[J]. Control Engineering Practice, 2007, 9(12): 1353−1360.

[6] ZHANG Haitao, LI Hanxiong, CHEN Guanrong. Dual-mode predictive control algorithm for constrained Hammerstein systems[J]. International Journal of Control, 2008, 81(10): 1609−1625.

[7] Arefi M M, Montazeria A, Poshtana J, et al. Wiener neural identification and predictive control of a more realistic plug flow tubular reactor[J]. Chemical Engineering Journal, 2007, 138(1/2/3): 274−282.

[8] Piche S, Sayyar-Rodsari B, Johnson D, et al. Nonlinear model predictive control using neural networks[J]. IEEE Control Systems Magazine, 2000, 20(3): 53−62.

[9] 李妍, 毛志忠. 基于多面体终端域的Hammerstein-Wiener非线性预测控制[J]. 自动化学报, 2011, 37(5): 629−638. LI Yan, MAO Zhizhong. Predictive control of Hammerstein- Wiener nonlinearity based on poly-topic terminal region[J]. Acta Automatica Sinica, 2011, 37(5): 629−638.

[10] Cervantes A L, Agamennoni O E, Figueroa J L.A nonlinear model predictive control system based on Wiener piece wise linear models[J]. Journal of Process Control, 2003, 13(7): 655−666.

[11] 师五喜. 未知多变量非线性系统自适应模糊预测控制[J]. 控制理论与应用, 2011, 28(1): 1399−1405. SHI Wuxi. Adaptive fuzzy predictive control for unknown multivariable nonlinear systems[J]. Control Theory & Applications, 2011, 28(1): 1399−1405.

[12] Peng H, Nakano K, Shioya H. Nonlinear predictive control using neural nets-based local linearization ARX model-stability and industrial application[J]. IEEE Transaction on Control Systems Technology, 2007, 15(1): 130−143.

[13] Peng H, Kitagawa G, Wu J, et al. Multivariable RBF-ARX model-based robust MPC approach and application to thermal power plant[J]. Applied Mathematical Modeling, 2011, 35(7): 3541−3551.

[14] Wu J, Peng H, Ohtsu K, et al. Ship’s tracking control based on nonlinear time series model[J]. Applied Ocean Research, 2012, 36(6): 1−11.

[15] ZHANG Yan, CHEN Zengqiang, YUAN Zhuzhi. Nonlinear system PID-type multi-step predictive control[J]. Journal of Control Theory and Applications, 2004, 2(2): 201−204.

[16] 李韬, 陈增强, 张纪峰. 比例积分型广义预测控制系统的稳定性分析[J] 控制理论与应用, 2007, 24(1): 19−25. LI Tao, CHEN Zengqiang, ZHANG Jifeng. Stability analysis of systems with proportional-integral generalized predictive control[J]. Control Theory & Applications, 2007, 24(1): 19−25.

[17] Peng H, Ozaki T, Haggan-Ozaki V, et al. A parameter optimization method for radial basis function type models[J]. IEEE Transaction on Neural Networks, 2003, 14(2): 432−438.

An improved multivariable RBF-ARX model-based nonlinear model predictive control approach and application

ZENG Xiaoyong1, 2, PENG Hui1, WU Jun1

(1. School of Information Science and Engineering, Central South University, Changsha 410083, China; 2. School of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410076, China)

For a class of smooth nonlinear multivariable systems whose working-points vary with time, a Gaussian radial basis function (RBF) neural networks-based local linearization autoregressive with exogenous (ARX) model was built to describe the system’s global behavior, and an improved nonlinear model predictive control (NMPC) method with adaptive differential effect based on RBF-ARX model identified offline was presented. Difference from conventional NMPC, the differential of errors between model outputs and designed outputs in whole prediction horizon were considered and their weights were adapted by functions of themselves in each optimization process, thus the controller can improve dynamic performance when the steady-state performance is ensured. A case study on a quadrotor for its real attitude control indicates that the proposed method is effective.

RBF-ARX model; nonlinear model predictive control; quadrotor

10.11817/j.issn.1672-7207.2015.10.022

TP 273

A

1672−7207(2015)10−3710−08

2015−03−10；

2015−06−19

国家自然科学基金资助项目(71271215，71221061)；国家国际科技合作计划项目(2011DFA10440)；湖南省教育厅项目(12C0021)(Projects (71271215, 71221061) supported by the National Natural Science Foundation of China; Project (2011DFA10440) supported by the International Science & Technology Cooperation Program of China; Project (12C0021) supported by the Hunan Provincial Education Department)

彭辉，教授，博士生导师，从事复杂非线性系统的建模与优化控制；E-mail：huipeng@csu.edu.cn

(编辑 陈爱华)