基于隐马尔可夫模型的网络安全态势预测方法
文志诚,陈志刚
基于隐马尔可夫模型的网络安全态势预测方法
文志诚1,2,陈志刚1
(1. 中南大学信息科学与工程学院,湖南长沙,410083;2. 湖南工业大学计算机与通信学院,湖南株洲,412007)
为了给网络管理员制定决策和防御措施提供可靠的依据,通过考察网络安全态势变化特点,提出构建隐马尔可夫预测模型。利用时间序列分析方法刻画不同时刻安全态势的前后依赖关系,当安全态势处于亚状态或偏离正常状态时,采用安全态势预测机制,分析其变化规律,预测系统的安全态势变化趋势。最后利用仿真数据,对所提出的网络安全态势预测算法进行验证。访真结果验证了该方法的正确性。
网络安全态势;隐马尔可夫;态势预测;参数学习;预测模型
Bass等[1−3]于2000年提出网络态势感知(CSA)的概念,详细介绍了网络态势感知的起源、概念、目标和特点等。然而,网络安全态势是网络态势的一种,一般通过感知技术来获取,是指对关联网络安全的各要素进行获取、理解、显示以及预测未来发展趋势,综合各方面的安全因素,从整体动态上反映网络当前安全状况,并对未来发展趋势及发展方向进行预测预警,为策略制定提供可靠的参照依据。网络安全态势主要强调环境、动态性以及实体之间的相互关联性,是一种状态、一种趋势、一个整体和宏观全局的概念,任何单一状况不能称为态势。在现实中,虽然传统的安全设备和异常检测设备得到了广泛应用[4−5],但主要从不同视角描述网络安全状态,基本上没有从宏观的角度为网管人员提供一个清晰整体的网络安全状况。目前大多数学者用一个适当的数值来表示当前安全态势,也有一些用五等化“高、中高、中、中低、低”或“1,2,3,4和5”描述安全态势。近年来,网络态势感知技术已逐渐地应用于计算机网络中,有望解决网络安全与管理问题。研究者提出了一些感知方法[6−8],但还没有成熟的模型、方法和评价标准。张海霞等[9]提出了基于攻击能力增长的网络安全分析模型,对网络安全性能方面进行了分析;谢丽霞等[10]针对网络安全态势感知问题,提出了一种基于神经网络的网络安全态势感知方法;唐成华等[11]针对安全态势评估正确性和合理性等问题,提出了基于D-S融合知识的网络安全态势评估方法;席荣荣等[12]给出了基于神经网络和隐马尔可夫的网络安全态势感知方法。有必要对安全态势未来发展趋势进行预测,为增强网络安全性提供可靠的参照依据。目前,对态势发展趋势及预测准确度还不够。唐成华等[13]提出了一种基于似然BP的网络安全态势预测方法,但该方法参数训练过程比较复杂,收敛速度也较慢。黄同庆等[14]从理论与实际相结合的角度提出一种基于隐Markov模型的实时网络安全态势预测模型HMM-NSSP,并给出了实时预测网络安全态势的方法。邬书跃等[15]将隐马尔可夫模型运用到异常用户行为的识别当中,算法从用户的Shell命令序列中提取特征。刘玉岭等[16]提出了基于时空维度分析的网络安全态势预测方法,从攻击方、防护方和网络环境3方面提取评估要素,在空间维度上分析各安全态势要素集及其相互影响关系对网络安全态势的影响,从而得出网络的安全态势。为了可靠地给网络管理员制定决策和防御措施提供依据,本文作者采用隐马尔可夫模型(hidden Markov model, HMM)的时间序列方法,刻画不同时刻安全态势的前后依赖关系,分析其变化规律,预测变化趋势及发展方向。其基本思路是:建立相应的隐马尔可夫预测模型,收集外部可观测状态数据及内部状态总数训练隐马尔可夫模型,当安全态势异常时,通过监测器采集样本数据,利用已训练好HMM对运行时的安全态势进行预测。
1 隐马尔可夫模型
隐马尔可夫模型(HMM)是一个双重随机过程,具有一定状态数的隐马尔可夫链和显示随机函数集,适合描述有隐含未知参数的马尔可夫过程。自20世纪80年代以来,HMM已被应用于语音识别,取得重大成功。到了20世纪90年代中期,HMM还被应用于计算机文字识别与移动通信核心技术“多用户的检测”。此外,HMM在生物信息科学和故障诊断等领域也开始得到应用。设模型的观察序列为=(1,2,…,T),则隐马尔可夫模型可由一个五元组=(,, π,,)对系统进行描述。在此五元组中,HMM模型中具有个隐状态,可记为=(1,2,…,S);每个隐状态S对应的有个可观测的状态V,记为=(1,2,…,v)。其中:π为1×阶初始概率分布矩阵,表示可观测序列在某时刻=1时,隐状态1时所在各个隐状态的初始所处于状态的概率分布情况。设初始状态矩阵π=(1,2,…,N),则有:
2)=(a)×,为马尔可夫链的状态概率转移矩阵,对一阶HMM,有

1≤≤;1≤≤;
3)=(b)×为符号概率观测矩阵,有
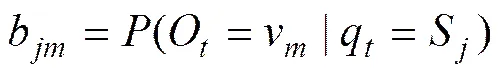
由上可知:模型中的转移矩阵的每行分别相加之和为1,即从一个状态转移到其他所有隐状态的概率之和为1,矩阵称为随机矩阵。随机矩阵与矩阵的情况类似。
2 预测模型
2.1 网络安全态势
在网络态势方面,国内外相关研究多见于军事战场的态势获取,网络安全领域的态势获取研究尚处于起步阶段,还未有普遍认可的解决方法。张海霞等[9]提出了一种计算综合威胁值的网络安全分级量化方法。该方法生成的态势值满足越危险的网络实体,威胁值越高。本文定义网络安全态势由网络基础运行性(runnability)、网络脆弱性(vulnerability)和网络威胁性(threat)三维组成,从3个不同的维度(或称作分量)以直观的形式向用户展示整个网络当前安全态势A=( runnability, vulnerability, threat)。每个维度可通过网络安全态势感知,从网络上各运行组件经信息融合而得到量化分级。为了方便计算实验与降低复杂度,本文中,安全态势每个维度取“高、中、差”或“1,2,3”共3个等级取值。本文主要进行网络安全态势预测。
2.2 构建预测模型
隐马尔可夫模型易解决一类对于给定的观测符号序列,预测新的观测符号序列出现概率的基本问题。隐马尔可夫模型是一个关于可观测变量与隐藏变量之间关系的随机过程,与安全态势系统的内部状态(隐状态)及外部状态(可观测状态)相比,具有很大的相似性,因此,利用隐马尔可夫模型能很好地分析网络安全态势问题。本文利用隐马尔可夫的时间序列分析方法刻画不同时刻安全态势的前后依赖关系。
已知时刻网络安全态势,预测+1,+2,…,+时刻可能的网络安全态势。以网络安全态势的网络基础运行性(runnability)、网络脆弱性(vulnerability)和网络威胁性(threat)三维组成隐马尔可夫模型的外在表现特征,即可观测状态或外部状态,它们分别具有“高、中、差” 或“1,2,3”取值,则安全态势共有33=27种外部组合状态。模型的内部状态(隐状态)为安全态势A的“高、中高、中、中差、差”取值。注意:在本文中外部特征的3个维度,每个维度三等取值,而内部状态A为五等取值。模型示例如图1所示。

图1 网络安全态势HMM模型示意图
网络安全态势A一般以某个概率a在“高、中高、中、中差、差”这5个状态之间相互转换,从一个状态向另一个状态迁移,这些状态称为内部状态或隐状态,外界无法监测到。然而,可以通过监测工具监测到安全态势外在的表现特征,如网络基础运行性(runnability)、网络脆弱性(vulnerability)和网络威胁性(threat)三维。监测到的这些参数值组合一个整体可以认为是一个可观测状态(外部状态,此观测状态由个分量构成,是1个向量)。图1中,设状态1为安全态势“高”状态,状态5为安全态势“差”状态。在实际应用中,根据具体情况可自行设定,本文取安全态势每维外在表现特征=3,则有27种安全态势可观测外部状态,而其内部状态(隐状态)共为5种。
定义1:设网络安全态势A内部隐状态可表示为1,2,…,5,则网络安全态势将在这5个隐状态之间以某个概率a自由转移,其中0≤a≤1。
定义2:网络安全态势A外在表现特征可用个随机变量x(1≤≤, 本处=3)表示,令=(1,2,…,x)构成1个维随机变量;在时刻,1次具体观测o的观测值表示为v,则经过个时刻对观测得到1个安全态势状态观测序列={1,2,…,o}。
本文基本思路是:建立相应的隐马尔可夫模型,收集内、外部状态总数训练隐马尔可夫模型;当网络安全态势异常时,通过监测器收集网络外在表现特征数据,利用已训练好HMM的模型对网络安全态势进行预测,为管理员提供决策服务。
2.3 参数学习
前面建立了如何建立安全态势预测的隐马尔可夫模型=(,,)(其中,,和为未知参数)。隐马尔可夫预测模型能真正地起预测作用。参数学习的基本思路是:通过计算个最大化安全态势观测训练序列样本得出似然HMM模型,即找出使最大化的模型,使用Baum-Welch算法(向前向后算法)。从给定的观测序列组成安全态势的样本训练集,通过训练学习得到产生训练集的概率最大化即最有可能解释这个样本的HMM模型。
为了能使参数学习正常进行,之前要对HMM模型的3个参数赋予先验值即先验概率PPT,可根据高斯分布(也称正态分布)来指导赋予先验概率,而不是凭空臆想,具有客观性。
引理1 设随机变量~(,2),则密度函数为。每个维度看成1个随机变量,具有独立同分布性质。
根据概率论知识,可将随机变量观测值划分为5个互不相交的区间Si:(−∞,−3)(+3, +∞),(−3,−2.5)(+2.5,+3),(−2.5,−2)(+2,+2.5),(−2,)(+,+2和[μ−σ,+]。经计算,这5个区间Si(=0~4)对应的概率Si分别为0.26%,0.98%,3.32%,27.18%和68.26%。事实上,网络安全态势在绝大多数情况下处于“高”或“中高” 2种状态,其他3种状态较少。这5个层次取值基本上符合实际网络安全态势的运行情况,等级“差”的情况一般会落在3倍根方差3区域之外。其中,和都是常量,可通过大样本无偏估计得到。因此,按这5个区间的划分可以对应于安全态势“差、中差、中、中高、高”5个等级所占用的概率,作为它们的先验值。具体操作如下。
1) 给定这安全态势5个隐状态的初始先验概率π时,5个区间Si(=0~4)对应5个安全态势等级“差、中差、中、中高、高”,其5个区间概率Si分别为0.26%,0.98%,3.32%,27.18%和68.26%。从物理意义上看,每个隐状态的初始状态处于等级“高”要比处于“低”的概率大,符合实际情况。
2) 对于给定随机矩阵的先验概率,在安全态势“高”状态时,安全态势“高”状态转移到另一个安全态势“高”状态概率(11)应该也落在区域内,11为68.26%左右,而其他为31.74%左右,可根据实际情况给1i赋值。一般地,相邻等级状态的转移概率高。其他隐状态的转移概率可类似求出。
3) 赋予随机矩阵的先验概率时,在安全态势“高”状态下,其可观测的状态有≤327种可能,在此时最大可能应该是安全态势“高”状态可观测状态(即个特征都取安全态势“高”那个组合状态)。假设可观测状态1为安全态势“高”状态可观测状态,则其概率11为68.26%左右,而其他可观测的安全态势“高”状态2, ...,v概率为31.74%左右,可按分级赋予。
在本文中,使用隐马尔可夫模型Baum-Welch学习算法,从训练样本中逐渐学习得到模型的3个参数,它是一种EM迭代方法。在每次迭代过程中,首先初始化,再进行E-步,在给定的(,,)时计算和;最后进行M-步,在给定公式和的情况下再计算模型λ。这2步交替迭代,进行直到完全收敛为止。
2) E-步:在给定的和观测的条件下计算和。
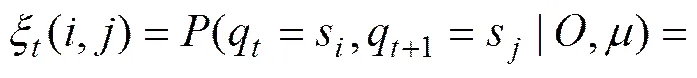
其中:
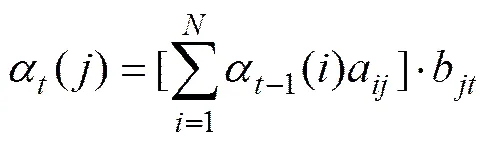
根据EM算法,通过样本学习,可以得到本网络安全态势HMM模型中的3个未知参数,和B。引理1在给3个参数的先验概率PPT时有严格的理论基础。
3 预测算法
在局域网中,当网络运行不正常或对其网络运行性能产生怀疑时,通过对网络安全态势个外在表现特征监测,得到个时刻的可观测状态(三维组合状态),根据已建立的隐马尔可夫模型预测网络安全态势未来发展状况,及时调整安全策略,为高层决策服务提供可靠依据。
预测算法的基本思路是:给定1个已训练好的HMM及1个观测序列(1,…,O),希望找出隐状态序列=(1,2,…,q),其具有产生安全态势可观测序列的最大概率的可能。即要找到使(|,)最大化的*,则在最大化安全态势隐状态序列*=(1,…,q)的个隐状态中,下一个非常可能出现的隐状态q+1即为需要预测的状态,它是可观测状态q向下一个状态转移过程中转移概率a中最大的隐状态q+1,即1时刻的网络安全态势。算法 如下。
1) 令观测在时刻的数据隐状态q为S,可得到沿着隐状态状态路径=(1,2,…,q)(其中:q−1=S,q=S),产生安全态势可观测序列=(1,…,t),的最大输出概率为δ(,),有(2≤≤;1≤≤)。其中:φ()为记录最大概率状态路径上当前安全态势的隐状态q的前一个状态,(2≤≤;1≤≤)。arg max表示寻求最大参数值,使得表达式结果为 最优。
4)根据隐状态T*对应的输出序列和可观测概率随机矩阵,计算此状态的最大输出概率,再计算1时刻的输出,得到+1时刻状态:。
算法中计算δ()时必须考虑从−1时刻所有个状态转移到状态的S概率,时间复杂度为(),对应每个时刻,要计算个中间变量δ(),…,δ(),时间复杂度为(2),因为1,…,,因此,整个算法时间复杂度为(2)。
4 仿真实验
为了检验本文所提出的网络安全态势预测理论的正确性,进行仿真实验。在实验过程中,2类数据来源如下:一类通过开发安装在各个网络组件上的软件监测得到的实时数据;一类来源于Snort入侵检测系统中的观测数据。基本步骤如下:首先,按引理1赋给隐马尔可夫模型=(,,)这3个参数的先验值;其次,按照一定规则随机采集样本训练HMM模型直至收敛,获得3个参数的近似值;最后,由一组网络安全态势样本观测序列预测下一阶段态势。
4.1 网络模型
根据本文所提出的网络安全态势预测理论搭建网络实验环境,如图2所示。图2中正常用户User和攻击者Attacker都可通过因特网访问网络主机,主机有数据库服务器、FTP服务器和入侵检测系统等。本文模拟攻击者Attacker 在不同时刻对网络上不同类型的主机发起扫描、缓冲区溢出攻击和TCP-SYN Flood 攻击等,通过获取入侵检测系统IDS报警日志信息对节点单位时间内受到的攻击进行统计,根据网络安全态势感知方法可获取整个网络安全态势A,再根据文中HMM模型预测下一阶段的网络安全态势。
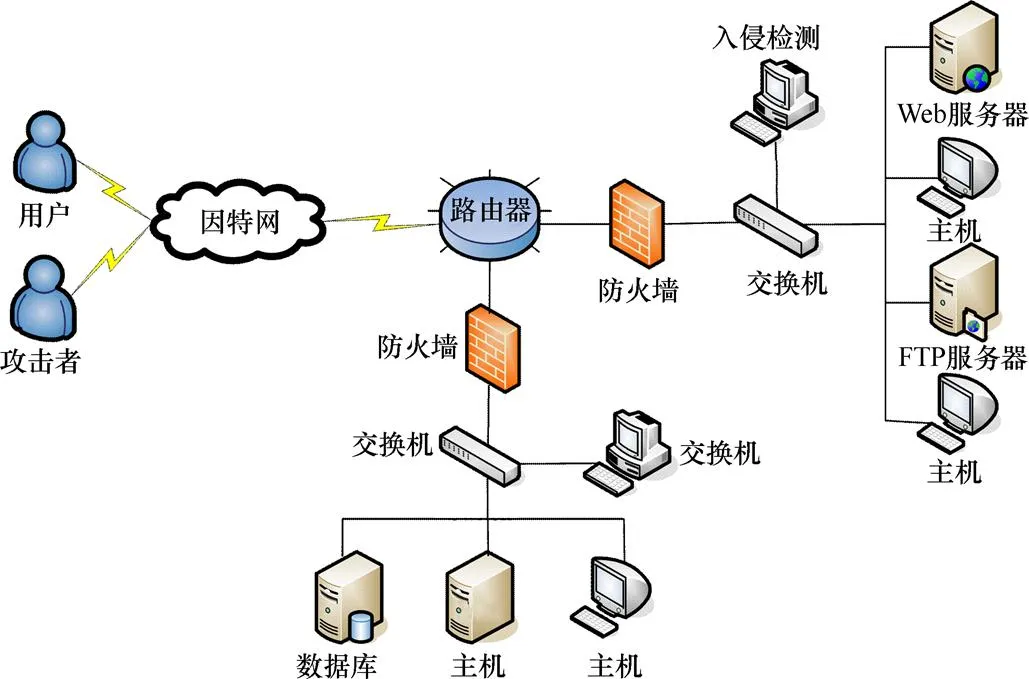
图2 实验环境网络拓扑图
4.2 数据预处理
网络基础运行性(runnability)、网络脆弱性(vulnerability)和网络威胁性(threat)取三等值“高、中、差”或“1,2,3”,则总共可观测组合状态=27个。当这3个特征取定值时,则1个可观测组合状态可表示为=(runnability, vulnerability, threat)。对这27个状态编号为:1=(1,1,1),2=(1,1,2),3=(1,1,3),4=(1,2,1)等。按引理1给定=(,,)先验值如表1~3所示。从表3可见:当安全态势的隐状态为“高”时(1行),观测到正常可观测安全状态1的概率为68.26%,其他情况按概率就近转移为大的原则,小概率平均状态数,3个参数的先验概率值近似给定。

表1 参数π的先验值PPT

表2 状态转移随机矩阵A的先验值aij

表3 观测随机矩阵B的先验值bjm
4.3 训练隐马尔可夫模型
从图2可获取网络的安全态势A,则外在观测=(runnability, vulnerability, threat)取定相应值。若在时间观测到的值就是O,则取个样本序列来训练隐马尔可夫模型直致收敛,得到其似然模型,即可确定3个参数。按照上述网络安全态势所提出的理论,由于本文取安全态势分量数为3,则对于每个观测样本取其长度为=3,即有形如观测样本。假设网络安全态势正常情况下的概率为95%左右,其他情况共为5%左右。仿真样本的获取通过随机程序产生,共采取2次观测样本量为2 000和3 000个,其收敛效果如图3所示。图3中,横坐标代表迭代所需次数,纵坐标表示经过每次迭代后3个参数值与前次迭代结束时3个参数值的距离即方差。为了便于绘图,将所有的概率放大100倍。通过样本训练,可以得到模型λ的3个隐马尔可夫模型参数的估计值。图3所示为本文赋予先验概率收敛算法及未赋予先难概率收敛算法对比效果。

样本量/个:1—2 000,赋予先验概率; 2—2 000,未赋予先验概率;3—3 000,赋予先验概率; 4—3 000,未赋予先验概率
对上述实验结果进行分析可得:1) 利用隐马尔可夫预测模型,通过获取外在预测数据,以此来训练HMM,具有高效的收敛算法,数据量达到3 000个以上,基本上收敛在某个点上,说明预测模型可行。隐马尔可夫预测模型在参数学习时,给定先验概率,收敛速度优于传统的HMM参数学习方法。2) 利用训练好的隐马尔可夫预测模型,根据临时监测的网络安全态势,基于预测算法,可方便地预测下一时刻网络的安全态势(如图4所示),因此,本算法是有效的。
4.4 安全态势预测
在网络运行时,若怀疑网络安全态势异常,则通过监测一定数量的安全态势观测序列,经过寻找隐马尔可夫模型最有可能解释产生本次安全态势观测的一系列隐状态。基于隐状态q,则它的下一个最大可能转移概率a的相应隐状态在+1时刻的安全态势A为q+1。
本实验采集一组10个观测样本数据为:<高、高、高>,<高、高、高>,<高、中、高>,<高、中、中>,<中、中、中>,<中、中、中>,<中、中、高>,<中、高、高>,<高、高、高>和<高、高、高>。输入到隐马尔可夫模型中,经解码为安全态势隐状态:“高、高、中高、中高、中、中、中高、中高、高、高”。最后1个隐状态q=“高”。由于11=0.682 6,在所有的隐状态转移概率中为最高,所以,在+1时刻的安全态势A为q1=“高”。网络安全态势预测对比图如图4所示,其中,纵轴表示安全态势等级,“5”表示“高”,“0”表示“低”;横轴表示时间,在采样序号10时,安全态势为高,经预测下一个时刻11时,安全态势应该为高,可信度达68.26%。通过本实验,依据训练好的隐马尔可夫预测模式可方便地预测下一时刻的网络安全态势发展趋势。从图4可明显看出本文的HMM方法可信度比贝叶斯预测方法的高。

曲线中,数据个位数表示安全态势的等级,小数表示所处此等级的概率
5 结论
1) 为了可靠地给网络管理员制定决策和防御措施提供依据,建立预测安全态势的隐马尔可夫模型,参数训练其隐马尔可夫模型。当安全态势出现异常时,采用预测机制,通过收集网络外在可观测状态,利用已训练好HMM的模型对运行时安全态势进行实时预测。
2) 以正态分布为基础建立模型,对连续型随机变量经过离散化,操作方便且符合实际情况,有利于隐马尔可夫模型的参数学习。尤其对模型中的先验概率值确定有严格理论依据。仿真实验结果验证了本文方法的正确性。
[1] Bass T. Intrusion detection systems and multisensor data fusion[J]. Communications of the ACM, 2000, 43(4): 99−105.
[2] 龚正虎, 卓莹. 网络态势感知研究[J]. 软件学报, 2010, 21(7): 1605−1619. GONG Zhenghu, ZHUO Ying. Research on cyberspace situational awareness[J]. Journal of Software, 2010, 21(7): 1605−1619.
[3] Jeffrey M, Bradshaw, Carvalho M, et al. Sol: An agent-based framework for cyber situation awareness[J]. Künstliche Intelligenz: Springer, 2012, 26(2): 127−140.
[4] Görnitz N, Kloft M, Rieck K, et al. Toward supervised anomaly detection[J]. Journal of Artificial Intelligence Research, 2013, 46(2): 235−262.
[5] Sample C, Schaffer K. An overview of anomaly detection[J]. IT Professional, 2013, 15(1): 8−11.
[6] Giusj D, Chiara F, Gabriele O, et al. Aware online interdependency modeling via evidence theory[J]. International Journal of Critical Infrastructures, 2013, 9(1): 74−92.
[7] Jan Bazan G, Bazan-Socha S, Buregwa-Czuma S, et al. Classifiers based on data sets and domain knowledge: A rough set approach[J]. Intelligent Systems Reference Library, 2013, 43(1): 93−136.
[8] 方研, 殷肖川, 孙益博. 基于隐马尔可夫模型的网络安全态势评估[J]. 计算机应用与软件, 2013, 30(12): 64−68. FANG Yan, YIN Xiaochuan, SUN Yibo. Network security situation assessment based on hidden Markov model[J]. Computer Applications and Software, 2013, 30(12): 64−68.
[9] 张海霞, 苏璞睿, 冯登国. 基于攻击能力增长的网络安全分析模型[J]. 计算机研究与发展, 2007, 44(12): 2012−2019. ZHANG Haixia, SU Purui, FENG Dengguo. A network security analysis model based on the increase in attack ability[J]. Journal of Computer Research and Development, 2007, 44(12): 2012−2019.
[10] 谢丽霞, 王亚超, 于巾博. 基于神经网络的网络安全态势感知[J]. 清华大学学报(自然科学版), 2013, 53(12): 1750−1760. XIE Lixia, WANG Yachao, YU Jinbo. Network security situation awareness based on neural networks[J]. Journal of Tsinghua University (Science & Technology), 2013, 53(12): 1750−1760.
[11] 唐成华, 汤申生, 强保华. D-S融合知识的网络安全态势评估及验证[J]. 计算机科学, 2014, 41(4): 107−110, 125. TANG Chenghua, TANG Shensheng, QIANG Baohua. Assessment ang validation of network security situation based on D−S and knowledge fusion[J]. Computer Science, 2014, 41(4): 107−110, 125.
[12] 席荣荣, 云晓春, 张永铮, 等. 一种改进的网络安全态势量化评估方法[J]. 计算机学报, 2015, 38(4): 749−758. XI Rongrong, YUN Xiaochun, ZHANG Yongzheng, et al. An improved quantitative evaluation method for network security[J]. Chinese Journal of Computers, 2015, 38(4): 749−758.
[13] 唐成华, 余顺争. 一种基于似然BP的网络安全态势预测方法[J]. 计算机科学, 2009, 36(19): 97−100, 168. TANG Chenghua, YU Shunzheng. Method of network security situation prediction based on likelihood BP[J]. Computer Science, 2009, 36(19): 97−100, 168.
[14] 黄同庆, 庄毅. 一种实时网络安全态势预测方法[J]. 小型微型计算机系统, 2014, 35(2): 303−306. HUANG Tongqing, ZHUANG Yi. An approach to real-time network security situation prediction[J]. Journal of Chinese Computer Systems, 2014, 35(2): 303−306.
[15] 邬书跃, 田新广. 基于隐马尔可夫模型的用户行为异常检测新方法[J]. 通信学报, 2007, 28(4): 38−43. WU Shuyue, TIAN Xinguang. Method for anomaly detection of user behaviors based on hidden Markov models[J]. Journal on Communications, 2007, 28(4): 38−43.
[16] 刘玉岭, 冯登国, 连一峰, 等. 基于时空维度分析的网络安全态势预测方法[J]. 计算机研究与发展, 2014, 51(8): 1681−1694. LIU Yuling, FENG Dengguo, LIAN Yifeng, et al. Network situation prediction method based on spatial-time dimension analysis[J]. Journal of Computer Research and Development, 2014, 51(8): 1681−1694.
Network security situation prediction method based on hidden Markov model
WEN Zhicheng1, 2, CHEN Zhigang1
(1. School of Information Science and Engineering, Central South University, Changsha 410083, China; 2. School of Computer and Communication, Hunan University of Technology, Zhuzhou 412007, China)
In order to help network administrators make correct decisions and take effective defense measures, a hidden Markov prediction model was put forward. The characteristics of network security situation changes were investigated, the time series analysis method was used to describe the dependent relationship between the former and the latter’s security situations in different time. When the security situation was deviated from its normal state, the change law was analyzed, and system change trend and development direction of security situation in the future were predicted by the prediction model. Finally, the network security situation prediction algorithm was verified using the simulation data. The simulation results verify the correctness of the method.
network security situation; hidden Markov model; situation prediction; parameter learning; prediction model
10.11817/j.issn.1672-7207.2015.10.019
TP311
A
1672−7207(2015)10−3689−07
2015−03−05;
2015−05−10
国家自然科学基金资助项目(61073186,61073104,60903058);中南大学博士后基金资助项目(2012年)(Projects (61073186, 61073104, 60903058) supported by the National Natural Science Foundation of China; Project (2012) supported by the Post Doctoral Fund of Central South University)
陈志刚,博士,教授,博士生导师,从事网络计算与分布式处理研究;E-mail:czg@csu.edu.cn
(编辑 陈灿华)

