地震作用下浅埋隧道动态稳定性的拟静力上限分析
张佳华,杨小礼,张标
地震作用下浅埋隧道动态稳定性的拟静力上限分析
张佳华,杨小礼,张标
(中南大学 土木工程学院,湖南 长沙,410075)
考虑非偏压与偏压2种情况,从能量的角度出发,采用拟静力法研究水平地震力与竖直地震力对浅埋隧道稳定性的影响。研究结果表明:在静态条件下,由本文极限分析法计算所得的结果非常接近于由极限平衡法计算所得结果,验证了本文方法的正确性;在参数分析中,随着侧压力比例系数的增加,竖直方向的围岩压力减小,水平方向的围岩压力增大,破裂角呈减小的趋势,而偏压对浅埋隧道的稳定性也有一定影响,但侧压力比例系数的影响更大;在采用进行动态稳定性分析时,水平地震效应系数增加,浅埋隧道的围岩压力与破裂角增大;当竖直地震效应比例系数增加时,浅埋隧道的围岩压力增大,破裂角却减小,且效果明显,可见竖直地震力与水平地震力一样,对浅埋隧道的稳定性有较大影响,在进行支护设计时不容忽略。
水平地震力;竖直地震力;定理;拟静力法
在我国交通运输业的快速发展中,隧道具有举足轻重的地位,然而,很多隧道都处于地震多发地带,经常会遭受到不同程度的破坏。人们总认为与地面建筑物相比,隧道应该具有更强的抗震性能,因此,关于隧道的抗震问题始终没有引起重视[1−2]。然而,事实上,地震对隧道的影响不容忽视。1976年,唐山地震导致该地区很多矿井受到了不同程度的破坏,剥落、开裂甚至坍塌;1995年,日本的阪神地震导致灾区内10%的山岭隧道发生了严重的破坏,人们这才意识到隧道抗震的重要性;1999年,我国台湾的集集地震导致发震断层25 km内的49座隧道受到了不同程度的破坏,其中严重受损的达25%,中等受损的达25%;而2008年,汶川地震更是给震源附近的隧道带来了巨大灾害,其中严重受损的高达73%,中等受损的也有22%[3−5]。近年来,一些学者开始关注和重视隧道的抗震问题,并且采用不同的方法研究地震对隧道稳定性的影响。严松宏等[6]以南京长江隧道为实例,基于弹簧−质量模型,研究地基阻尼比、地基与隧道刚度比等对沉管隧道地震响应的影响。李育枢等[7]采用动力有限元法对偏压隧道的洞口边坡进行了地震动力反应和稳定性研究,并且建立了相应的评价模型。章荣军等[8]采用合理的锚杆参数来提高隧道抗震性能,分析了静态和动态条件下锚杆与衬砌的受力特征、结构动力响应特征和最大响应值的变化规律,得出增加墙脚处的锚杆可以大幅度提高隧道抗震性能。杨小礼等[9]基于极限平衡理论,研究了水平地震力对浅埋偏压隧道稳定性的影响。然而,纵观国内外的研究,很多学者只考虑了水平地震力,忽略了竖直地震力的影响。而实际上,地震力既表现在水平方向上,又表现在竖直方向上[10]。为此,本文根据浅埋非偏压隧道和浅埋偏压隧道的破坏模式,基于极限分析法,考虑水平地震力和竖直地震力,采用拟静力法对浅埋隧道的稳定性进行研究,完善和补充地震力对浅埋隧道稳定性影响的研究,以便为今后浅埋隧道的抗震设计和施工提供参考。
1 基本原理
1.1 拟静力法
目前,对土工结构进行的动态稳定性分析通常采用拟静力法,其实质是将动态力影响等效成为静态力作用[11]。对于地震力,水平地震效应系数为h和竖直地震效应系数为v,且有
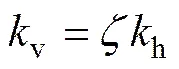
其中:h的取值范围为0~0.3;为竖直地震效应比例系数,一般取0.5,且正值表示方向向下,负值表示方向向上。为了单独研究水平地震力和竖直地震力对浅埋隧道稳定性的影响,在本文中,h分别取0,0.1,0.2和0.3;分别取−1.0,−0.5,0,0.5和1.0。
1.2 极限分析上限定理
极限平衡法在岩土工程中得到了推广和应用,但仍然存在一些不足,尤其是在计算过程中忽略了土体应力与应变的关系。而极限分析法却正好改正了这个缺点,它用一种理想的方式考虑了土体的本构关系即流动法则。因此,与极限平衡法相比,极限分析法的理论更加严谨完整,计算更加简单、方便,结果也更加真实、准确。根据Chen的观点,极限分析上限定理可表述为:构造一个运动许可的速度场,使其满足速度边界条件及应变与速度相容条件,则由虚功率方程式(1)所得到的荷载F一定大于或等于实际的破坏荷载[12]。

式中:F为极限荷载;为速度;为滑动面长度;为塑性区面积;为土体容重;和分别为塑性区土体的应力与应变;和分别为破坏面上土体的剪应力与正应力。
2 破坏模式
目前,关于浅埋隧道的破坏模式很多,最主要的有泰沙基法所采用的破坏模式和公路隧道设计规范所采用的破坏模式,如图1所示[13−14]。其中:泰沙基法所假定的破坏面就是图1中的折线1;公路隧道设计规范所假定的破坏面就是图1中的直线2。然而,在实际工程中,当隧道埋深不大时,开挖的影响将波及地表而不能形成“自然拱”;从施工过程中岩体(包括土体)的运动情况可以看到隧道开挖后若不及时支撑,则岩体会大量坍落或者移动,这种移动会影响到地表并且形成一个坍陷区域,此时岩体将会出现2个破坏面[13, 15]。所以,本文基于泰沙基法所采用的破坏模式和公路隧道设计规范所采用的破坏模式以及实际的工程经验,针对浅埋隧道提出了一种更接近于实际情况、更加合理的破坏模式,而这种破坏模式的破坏面也就是图1中的折线3。结合非偏压与偏压2种情况,得到浅埋非偏压隧道与浅埋偏压隧道的破坏模式,如图2和图3所示。其中:图2(a)和图2(b)所示分别为浅埋非偏压隧道的破坏模式及其相对应的速度场;图3(a)所示为浅埋偏压隧道的破坏模式,而图3(b)和图3(c)所示分别为与外侧结构相对应的速度场和与内侧结构相对应的速度场。图2和图3中:为隧道拱顶到水平地表面的垂直距离;为隧道洞径;隧道上覆岩体的速度为,而间断线上的速度分别0(),01()和1(),且速度与间断线之间的夹角均为内摩擦角;破裂角分别为()和()。
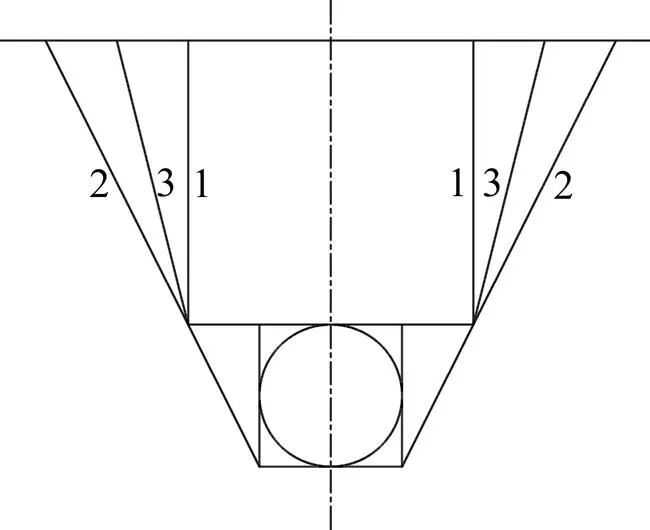
1—泰沙基法的破坏面;2—公路隧道设计规范的破坏面;3—本文破坏面
图1 浅埋隧道破坏模式的示意图
Fig. 1 Sketch of collapse mechanisms for shallow tunnel
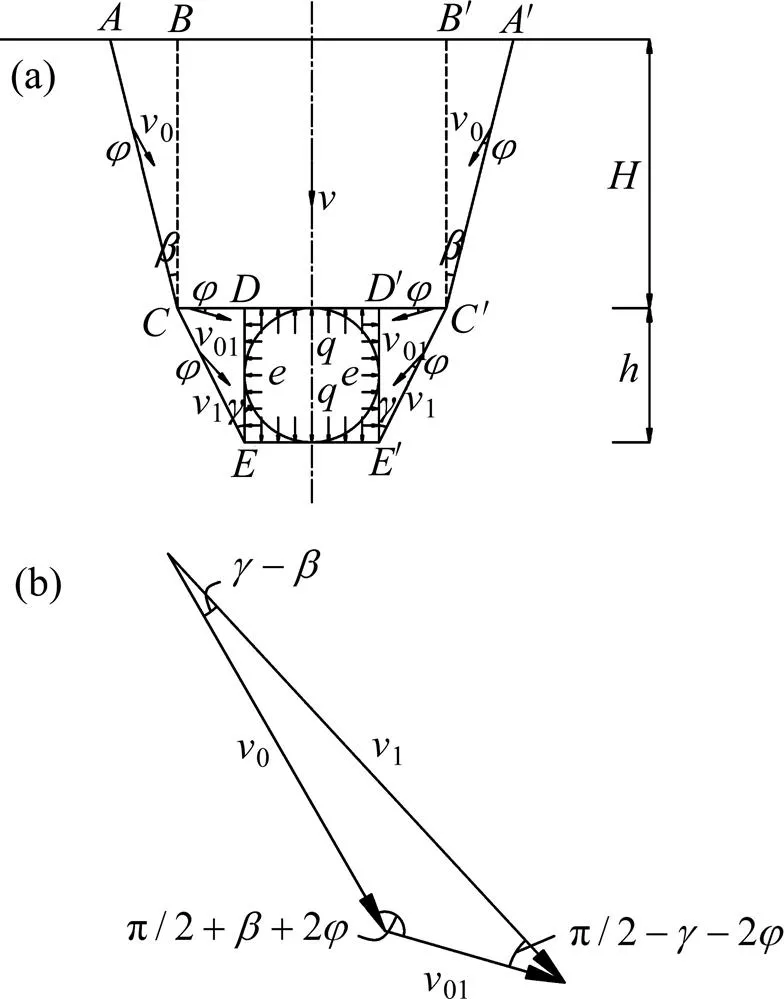
(a) 破坏模式;(b) 速度场
图2破坏模式及其
Fig. 2 Collapse mechanism and velocity field for shallow non-bias tunnel
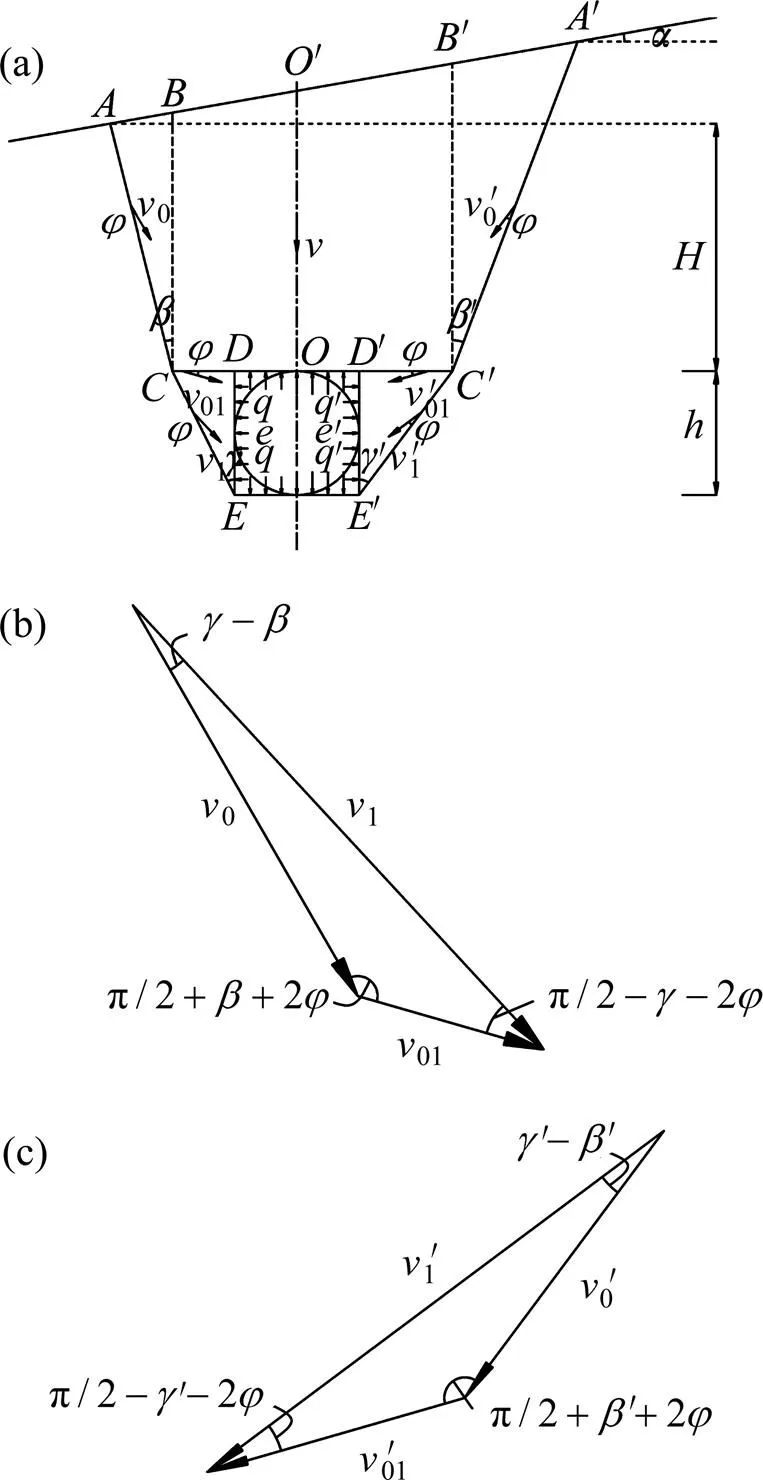
(a) 破坏模式;(b) 外侧结构的速度场;
(c) 内侧结构的速度场
图3 浅埋偏压隧道破坏模式及其相对应的速度场
Fig. 3 Collapse mechanism and velocity field for shallow bias tunnel
3 能量分析过程
将浅埋隧道简化成二维平面应变问题进行研究,采用极限分析上限定理计算时进行以下假定:1) 围岩为理想塑性材料,服从相关联流动规则;2) 隧道的破坏机理为左半边的结构产生外侧的破坏面,右半边的结构产生内侧的破坏面,圆形隧道简化成矩形隧道进行计算,则拱顶和拱底处的竖向均布支护力均为,边墙处的水平均布支护力均为,且,(其中,为侧压力比例系数,为土体重度);3) 采用拟静力法分析时,不考虑动态荷载对围岩物理参数的影响。
3.1 浅埋非偏压隧道围岩压力计算
3.1.1 速度关系
由于满足速度闭合条件,如图2(b)所示,则浅埋非偏压隧道破坏模式各速度为
3.1.2 外力所作功率
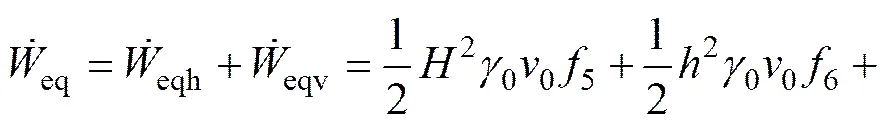
3.1.3 内部能量耗散率
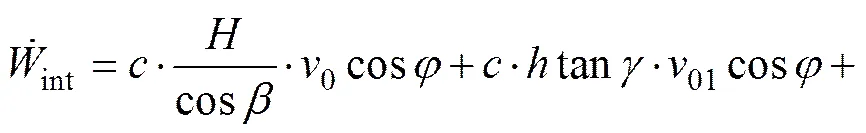
3.1.4 围岩压力
根据虚功率原理可得浅埋非偏压隧道竖向支护力的表达式为
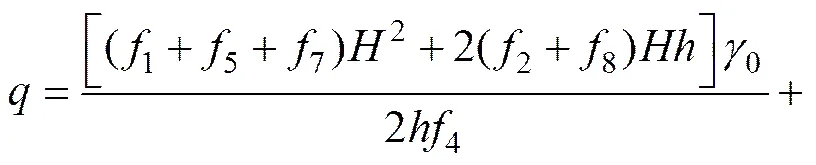
其中:
利用Matlab软件采用序列二次规划法可得到约束条件下围岩压力的优化解,其中约束条件为
3.2 浅埋偏压隧道围岩压力计算
以浅埋偏压隧道的外侧结构为例,具体推导围岩压力的解析解。
1) 速度关系。由于满足速度闭合条件,如图3(b)所示,外侧结构速度为
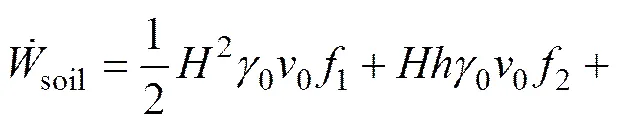
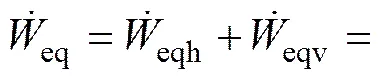
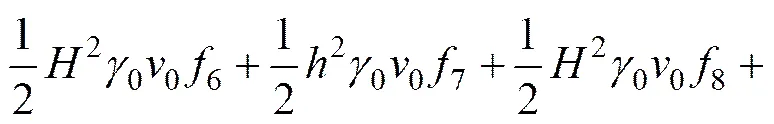
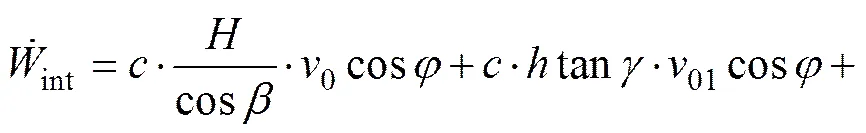
4) 围岩压力。根据虚功率原理可得浅埋偏压隧道外侧结构的竖向支护力为

其中:
利用Matlab软件采用序列二次规划法可得到约束条件下围岩压力的优化解,其中约束条件为
同理,内侧结构的围岩压力也可根据上述方法 求得。
4 静态稳定性分析
针对浅埋非偏压隧道和浅埋偏压隧道进行静态稳定性分析,其中参数假定:隧道埋深=20 m,跨度和高度=10 m,围岩容重20 kN/m3,内摩擦角18°,黏聚力=10.0 kPa,10°,h=0。
4.1 对比研究
为了验证本文方法的正确性,针对浅埋非偏压隧道和浅埋偏压隧道,将本文极限分析法所得到的计算结果与极限平衡法所得到的计算结果进行对比,结果如表1所示。由表1可得:对于浅埋非偏压隧道,由本文极限分析法所得计算结果比较接近由泰沙基极限平衡法所得计算结果;对于浅埋偏压隧道,当= 0.55~0.65时,由本文极限分析法所得计算结果比较接近由极限平衡法所得计算结果,从而验证了静态条件下文方法的正确性。
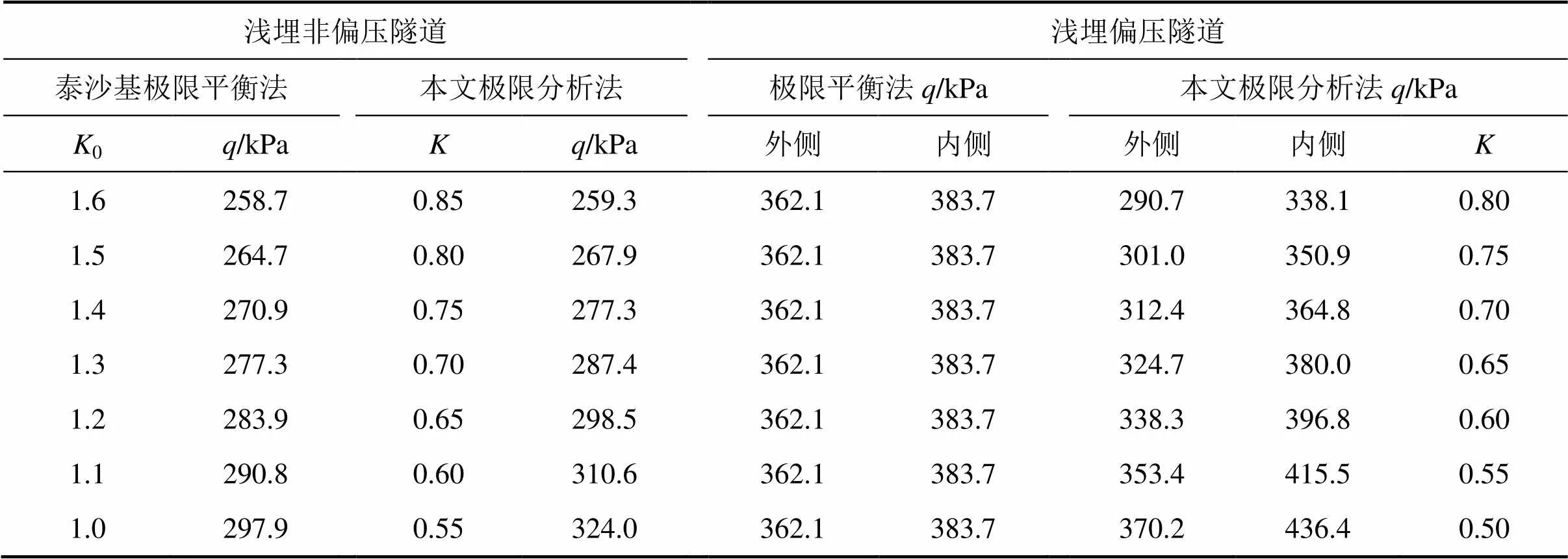
表1 本文极限分析法与极限平衡法计算结果对比
4.2 参数分析
4.2.1对围岩压力的影响
对围岩压力的影响见图4。从图4可得:1) 无论是浅埋非偏压隧道还是浅埋偏压隧道,无论是外侧结构还是内侧结构,竖直方向的围岩压力随的增加而呈非线性减小,水平方向的围岩压力随的增加而呈非线性变大,说明对于浅埋隧道,围岩压力与有关;2) 当一定时,浅埋偏压隧道的围岩压力大于浅埋非偏压隧道的围岩压力;而对于浅埋偏压隧道,内侧结构的围岩压力大于外侧结构的围岩压力。由此可见,偏压对浅埋隧道的围岩压力有一定的影响。综上所述,和偏压对浅埋隧道的围岩压力都有影响,但影响较大。
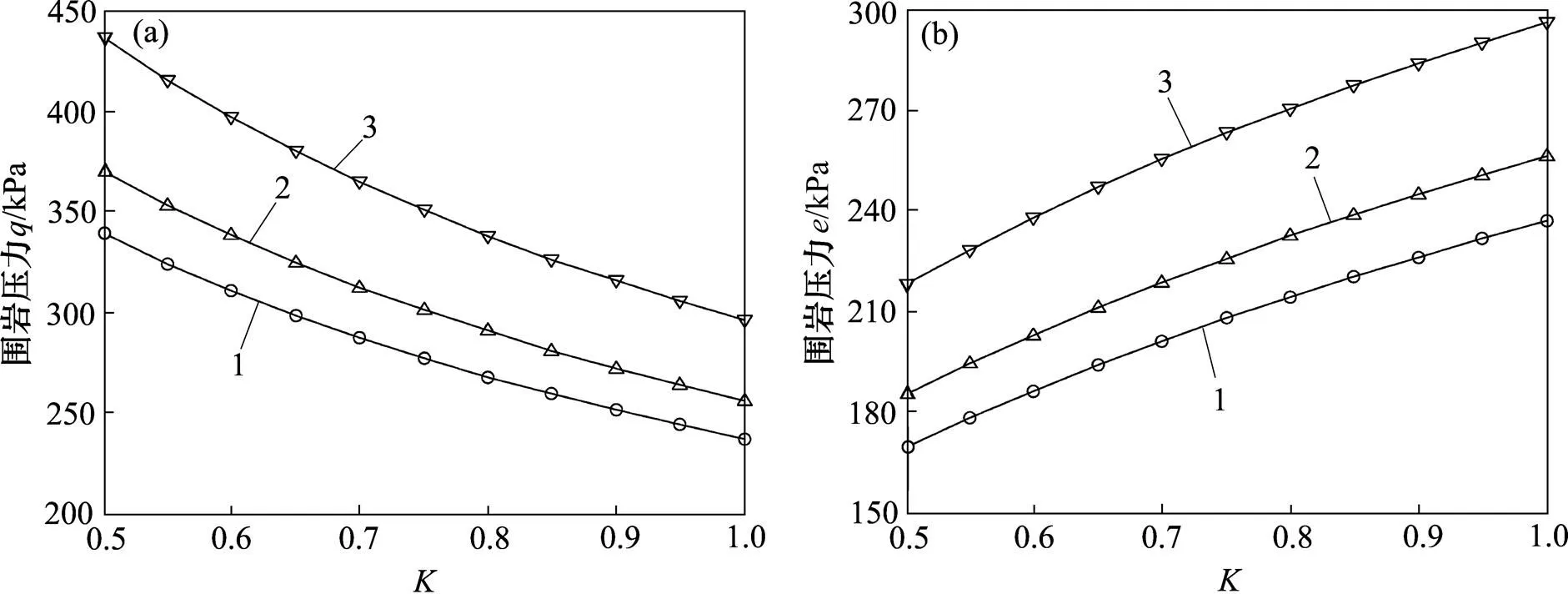
(a)−;(b)−
1—非偏压;2—偏压外侧;3—偏压内侧
图4对围岩压力的影响
Fig. 4 Influence ofon earth pressure
4.2.2对破坏模式的影响
对破坏模式的影响见图5。从图5可见:对于浅埋隧道,无论偏压与否,破裂角都随的增大呈减小的趋势;当一定时,浅埋偏压隧道的破裂角略大于浅埋非偏压隧道的破裂角;对于浅埋偏压隧道,内侧结构的破裂角略大于外侧结构的破裂角。综上所述,和偏压对浅埋隧道的破裂角都有一定的影响,但影响较大。
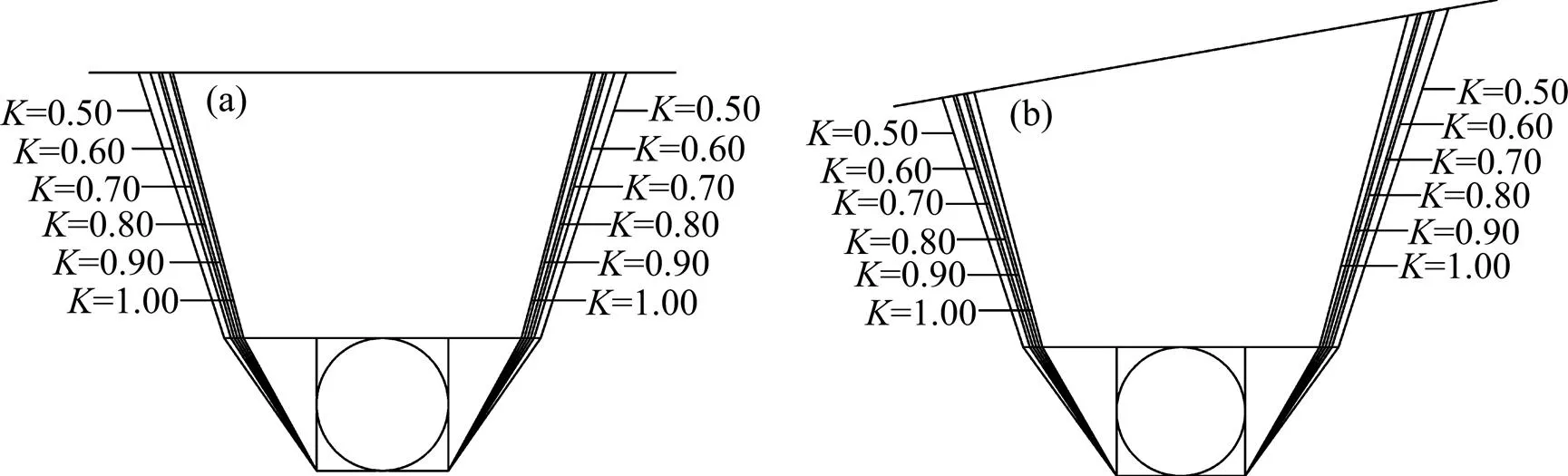
(a) 浅埋非偏压隧道;(b) 浅埋偏压隧道
图5对破坏模式的影响
Fig. 5 Influence ofon collapse mechanism
5 动态稳定性的拟静力分析
针对非偏压和偏压2种情况,采用拟静力法对浅埋隧道进行动态稳定性分析。为了单独研究水平地震力和竖直地震力对浅埋隧道稳定性的影响,假设只有水平地震力作用和水平地震力与竖直地震力同时作用2种情况。假定:隧道埋深=20 m,跨度和高度= 10 m,围岩容重20 kN/m3,内摩擦角18°,黏聚力=10.0 kPa,10°。
5.1 水平地震力对浅埋隧道稳定性的影响
5.1.1 水平地震效应系数对围岩压力的影响
水平地震效应系数对围岩压力的影响见图6。从图6可得:1)对于浅埋隧道,无论偏压与否,无论是外侧结构还是内侧结构,在水平地震效应下()的围岩压力都大于静态条件下()的围岩压力。2) 在水平地震力单独作用情况下(且),无论是浅埋非偏压隧道还是浅埋偏压隧道,无论是外侧结构还是内侧结构,水平地震效应系数所对应的围岩压力最小,而水平地震效应系数所对应的围岩压力最大。综上所述,当一定时,水平地震力对浅埋隧道的围岩压力有较大的影响,且围岩压力随水平地震效应系数的增加而变大。
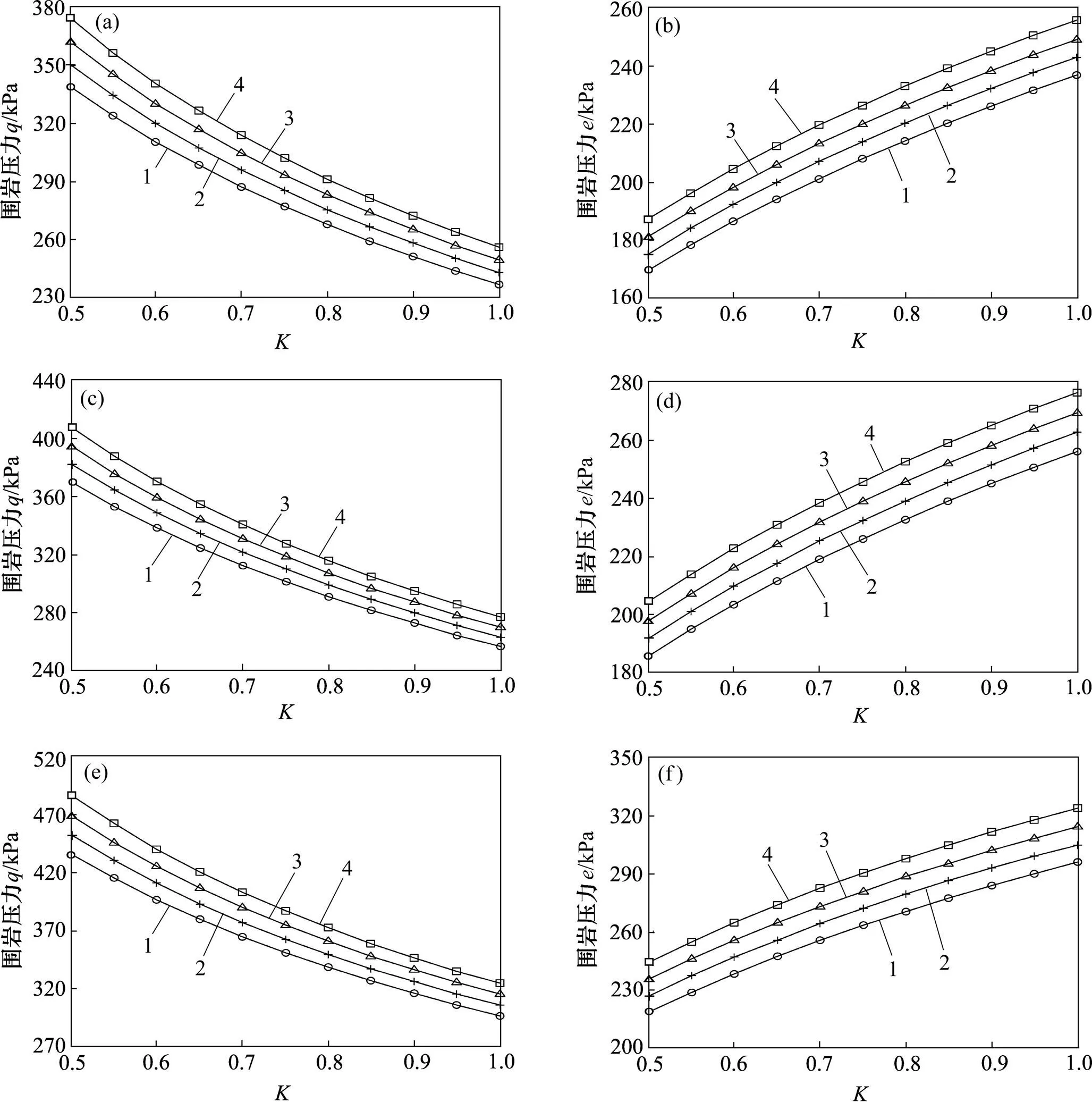
(a) 非偏压,h−−;(b) 非偏压,h−−;(c) 偏压外侧,h−−;(d) 偏压外侧,h−−;(e) 偏压内侧,h−−;(f) 偏压内侧,h−−
h: 1—0; 2—0.1; 3—0.2; 4—0.3
图6 水平地震效应系数h对围岩压力的影响
Fig. 6 Influence of horizontal seismic effect coefficienthon earth pressure
5.1.2 水平地震效应系数对破坏模式的影响
当=0.50~1.00时,浅埋隧道破坏模式的形状比较相似,所以只绘制出=0.50时不同水平地震效应系数h的破坏模式,如图7所示。由图7可得:对于浅埋非偏压隧道和浅埋偏压隧道,1) 在水平地震效应下()破坏模式的破裂角略大于静态条件下(h=0)的破裂角。2) 当只有水平地震力作用时(且),破裂角随水平地震效应系数h的增加呈变大的趋势。可见:当一定时,水平地震力对浅埋隧道的破裂角有一定影响,且破裂角随水平地震效应系数h的增加呈变大的趋势。

(a) 浅埋非偏压隧道;(b) 浅埋偏压隧道
图7 水平地震效应系数h对破坏模式的影响(=0.50)
Fig. 7 Influence of horizontal seismic effect coefficienthon collapse mechanism (=0.50)
5.2 竖直地震力对浅埋隧道稳定性的影响
5.2.1 竖直地震效应比例系数对围岩压力的影响
当水平地震效应系数h分别取0.1,0.2和0.3时,浅埋隧道围岩压力的变化规律大致相同,故只绘制出水平地震效应系数h=0.3时不同竖直地震效应比例系数的围岩压力,如图8所示。

(a) 非偏压,−−;(b) 非偏压,−−;(c) 偏压外侧,−−;(d) 偏压外侧,−−;(e) 偏压内侧,−−;(f) 偏压内侧,−−
: 1— −1.0; 2— −0.5; 3—0; 4—0.5; 5—1.0
图8 竖直地震效应比例系数对围岩压力的影响(h=0.3)
Fig. 8 Influence of vertical seismic proportional coefficienton earth pressure(h=0.3)
由图8可得:对于浅埋隧道,无论偏压与否,无论是外侧结构还是内侧结构,在水平地震效应系数h一定的条件下,当一定时,围岩压力的大小依次为:=1.0时最大,=0.5时较大,=0时居中,=−0.5时次之,而=−1.0时最小。故由此可得:1) 当竖直地震效应比例系数为负值时,水平地震力和竖直地震力同时作用下的围岩压力小于仅有水平地震力作用下的围岩压力;而当竖直地震效应比例系数为正值时,水平地震力和竖直地震力同时作用下的围岩压力大于仅有水平地震力作用下的围岩压力;2) 浅埋隧道围岩压力随竖直地震效应比例系数的增加而变大,且效果非常明显。综上所述,在水平地震效应系数h一定的条件下,当一定时,竖直地震力对浅埋隧道的围岩压力有较大的影响,且围岩压力随竖直地震效应比例系数的增加而变大。
5.2.2 竖直地震效应比例系数对破坏模式的影响
对于浅埋隧道,当水平地震效应系数h分别取0.1,0.2和0.3,=0.50~1.00时所对应的破坏模式形状比较相似,所以,只绘制出水平地震效应系数h=0.3、=0.50时不同竖直地震效应比例系数的破坏模式,如图9所示。由图9可得:1) 当竖直地震效应比例系数为负值时,水平地震力和竖直地震力同时作用下破坏模式的破裂角略大于仅有水平地震力作用下的破裂角;而当竖直地震效应比例系数为正值时,水平地震力和竖直地震力同时作用下破坏模式的破裂角略小于仅有水平地震力作用下的破裂角。2) 浅埋隧道破裂角随竖直地震效应比例系数的增大呈减小的趋势。综上所述,在水平地震效应系数h一定的条件下,当一定时,竖直地震力对浅埋隧道破裂角有一定的影响,且破裂角随竖直地震效应比例系数增大呈减小的趋势。

(a) 浅埋非偏压隧道;(b) 浅埋偏压隧道
图9 竖直地震效应比例系数对破坏模式的影响(h=0.3,=0.50)
Fig. 9 Influence of vertical seismic proportional coefficienton collapse mechanism (h=0.3,=0.50)
6 结论
1) 基于浅埋非偏压隧道和浅埋偏压隧道破坏模式,考虑水平地震力和竖直地震力,运用上限定理推导了围岩压力的解析解,结合约束条件,采用序列二次规划法得到了围岩压力的最优解。
2) 在静态条件下,针对浅埋非偏压隧道和浅埋偏压隧道进行了对比和参数分析。由本文极限分析法所得计算结果比较接近于由极限平衡法所得计算结果,验证了本文方法的正确性。在参数分析中,竖直方向围岩压力随的增加非线性减小,水平方向围岩压力随的增加呈非线性变大,破裂角随的增加呈减小的趋势;而偏压对围岩压力和破裂角也有一定的影响,但相比之下,的影响较大。
3) 针对浅埋非偏压隧道和浅埋偏压隧道,采用拟静力法进行了动态稳定性分析。在只有水平地震力作用的情况下,水平地震效应下的围岩压力大于静态条件下的围岩压力,且围岩压力随水平地震效应系数h的增加而变大。同样,水平地震效应下破坏模式的破裂角略大于静态条件下的破裂角,且破裂角随水平地震效应系数h的增加呈变大的趋势。在水平地震效应系数h一定的条件下,当竖直地震效应比例系数为负值时,水平地震力和竖直地震力同时作用下的围岩压力小于仅有水平地震力作用下的围岩压力;而当竖直地震效应比例系数为正值时,水平地震力和竖直地震力同时作用下的围岩压力大于仅有水平地震力作用下的围岩压力,且围岩压力随竖直地震效应比例系数的增加而变大。而与围岩压力不同的是,竖直地震效应比例系数对破裂角的影响却恰恰相反。
[1] Yang X L. Seismic passive pressure of earth structures by nonlinear optimization[J]. Archive of Applied Mechanics, 2011, 81(9): 1195−1202.
[2] Chen S L, Gui M W. Seismic performance of tunnel lining of side-by-side and vertically stacked twin-tunnels[J]. Journal of Central South University of Technology, 2011, 18(4): 1226−1234.
[3] Cilingir U, Madabhushi S P G. Effect of depth on the seismic response of square tunnels[J]. Soils and Foundations, 2011, 51(3): 449−457.
[4] Saada Z, Maghous S, Garnier D. Pseudo-static analysis of tunnel face stability using the generalized Hoek-Brown strength criterion[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(18): 3194−3212.
[5] WANG Zhengzheng, GAO Bo. Investigation and assessment on mountain tunnels and geotechnical damage after the Wenchuan earthquake[J]. Science in China Series E: Technological Science, 2009, 52(2): 546−558.
[6] 严松宏, 高峰, 李德武, 等. 沉管隧道地震响应分析若干问题的研究[J]. 岩石力学与工程学报, 2004, 23(5): 846−850.
YAN Songhong, GAO Feng, LI Dewu, et al. Studies on some issues of seismic response analyses for submerged tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(5): 846−850.
[7] 李育枢, 高广运, 李天斌. 偏压隧道洞口边坡地震动力反应及稳定性分析[J]. 地下空间与工程学报, 2006, 2(5): 738−743.
LI Yushu, GAO Guangyun, LI Tianbin. Analysis of earthquake response and stability evaluation for transverse slope at secund tunnel portal[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(5): 738−743.
[8] 章荣军, 郑俊杰, 杨庆年. 地震作用下浅埋隧道系统锚杆参数优化[J]. 华中科技大学学报(自然科学版), 2009, 37(5): 98−101.
ZHANG Rongjun, ZHENG Junjie, YANG Qingnian. Parameter optimization for systematic bolts of shallow tunnel under earthquake action[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2009,37(5):98-101.
[9] 杨小礼, 黄波, 王作伟. 水平地震力作用下浅埋偏压隧道松动围岩压力的研究[J]. 中南大学学报(自然科学版), 2010, 41(3): 1090−1095.
YANG Xiaoli, HUANG Bo, WANG Zuowei. Rock failure pressure of shallow tunnel subjected to horizontal seismic and unsymmetrical loads[J]. Journal of Central South University (Science and Technology), 2010, 41(3): 1090−1095.
[10] Kouretzis G P, Sloan S W, Carter J P. Effect of interface friction on tunnel liner internal forces due to seismic S- and P-wave propagation[J]. Soil Dynamics and Earthquake Engineering, 2013, 46: 41−51.
[11] 赵炼恒, 罗强, 李亮, 等. 层状岩体边坡动态稳定性拟静力上限分析[J]. 岩土力学, 2010, 31(11): 3627−3634.
ZHAO Lianheng, LUO Qiang, LI Liang, et al. Upper bound quasi-static analysis of dynamic stability of layered rock slopes[J]. Rock and Soil Mechanics, 2010, 31(11): 3627−3634.
[12] Chen W F. Limit analysis and soil plasticity[M]. Florida: J. Ross Publishing, Inc., 2007: 47−99.
[13] 杨小礼, 王作伟. 非线性破坏准则下浅埋隧道围岩压力的极限分析[J]. 中南大学学报(自然科学版), 2010, 41(1): 299−302.
YANG Xiaoli, WANG Zuowei. Limit analysis of earth pressure on shallow tunnel using nonlinear failure criterion[J]. Journal of Central South University (Science and Technology), 2010, 41(1): 299−302.
[14] JTG D70—2004, 公路隧道设计规范[S].
JTG D70—2004, Code for design of road tunnel[S].
[15] YANG Xiaoli, Jin Qiyun, MA Junqiu. Pressure from surrounding rock of three shallow tunnels with large section and small spacing[J]. Journal of Central South University, 2012, 19(8): 2380−2385.
Upper bound quasi-static analysis of dynamic stability on shallow tunnel under earthquake action
ZHANG Jiahua, YANG Xiaoli, ZHANG Biao
(School of Civil Engineering, Central South University, Changsha 410075, China)
Based on two cases of non-bias and bias, from the view of energy, the influence on stability of shallow tunnels from horizontal and vertical earthquake force was studied using the quasi-static method. The results show that on static condition, the results calculated by the limit analysis method are very close to those obtained by the limit equilibrium method, which verifies the correctness of this method. With the increment of proportional coefficient of lateral pressure, vertical earth pressure declines while horizontal earth pressure increases, and break angle shows decreasing trend. Effect of asymmetric loads on the stability of shallow tunnels is less than that of proportional coefficient of lateral pressure. The earth pressure and break angle both increase with the increase of the horizontal seismic effect coefficient. With the increase of vertical seismic proportional coefficient, the earth pressure increases but the break angle decreases obviously. Therefore, vertical earthquake force, just like horizontal earthquake force, has significant effect on the stability of shallow tunnels, which can not be neglected in the design of support structures.
horizontal earthquake; vertical earthquake; upper bound theorem; quasi-static method
U451
A
1672−7207(2015)01−0238−10
2014−01−20;
2014−03−22
国家自然科学基金资助项目(51378510,51178468);湖南省研究生科研创新项目(CX2013B077) (Projects(51378510, 51178468) supported by the National Natural Science Foundation of China; Project(CX2013B077) supported by Graduate Research and Innovation Projects in Hunan Province)
张佳华,博士研究生,从事隧道与地下工程方面的研究;E-mail: 124801035@csu.edu.cn
10.11817/j.issn.1672−7207.2015.01.032
(编辑 陈灿华)

