基于参数优化的最小二乘支持向量机HEV阀控铅酸蓄电池SOC预测
王琪,孙玉坤,黄永红
基于参数优化的最小二乘支持向量机HEV阀控铅酸蓄电池SOC预测
王琪1, 2,孙玉坤2, 3,黄永红1, 2
(1. 江苏大学 电气信息工程学院,江苏 镇江,212013;2. 江苏大学 机械工业设施农业测控技术与装备重点实验室,江苏 镇江,212013;3. 南京工程学院 电力工程学院,江苏 南京,211167)
针对电池容量预测问题,引入最小二乘支持向量机(LS-SVM)方法用于判断混合动力汽车(HEV)阀控铅酸蓄电池(VRLA)的荷电状态(SOC)。考虑到最小二乘支持向量机的参数选择会对预测结果产生较大的影响,提出一种基于参数优化的最小二乘支持向量机预测方法。首先,在非线性回归预测模型的训练过程中,采用模拟退火算法来确定LS-SVM的初始值参数,从而更好地反映预测模型的复杂度,以此提高状态预测的精度。其次,由于预测模型在应对不良数据时可能出现误差增大的问题,分别采用贝叶斯证据框架(BEF)优化算法和留一交叉验证(LOOCV)优化算法来增强预测模型的抗差能力。研究结果表明:留一交叉验证优化算法具有较高的预测精度,实用性强,有效性高。
蓄电池;荷电状态;最小二乘支持向量机;参数优化;预测
蓄电池是混合动力汽车的能源之一。为确保蓄电池性能良好、循环寿命长以及混合动力汽车的燃油经济性,须对蓄电池进行合理的管理和控制[1]。正如普通车辆必须监视油箱内燃油的容量一样,混合动力汽车也需要知道其车载电源能量,而荷电状态(SOC)是反映蓄电池能量的重要参数,所以,如何正确获得蓄电池SOC成为混合动力汽车应用的重要环节[2]。SOC作为蓄电池的内部特性不可以直接对其进行测量,只能通过对电压、电流、温度等一些直接测量的外部特性参数预测而得[3]。目前,国内外学者对蓄电池SOC进行了大量的研究,主要方法有:1) 基于安时计量的预测方法。安时计量法结构简单,操作方便,但是在应用中存在精度不高的缺陷[4]。2) 基于开路电压的预测方法。开路电压法是目前最常用的SOC预测方法之一,将稳定的开路电压直接表示蓄电池当前的容量,操作简单,但是在测量开路电压时,需考虑电池的电化学和热力学平衡,同时开路电压的稳定需要很长的时间[5]。3) 基于蓄电池内阻特性的预测方法。内阻法是将交流电注入到蓄电池,然后通过内阻和容量的关系来判断蓄电池当前容量,预测SOC极值时精度较高,但是内阻受蓄电池温度、静置时间和充放电初始状态等因素的影响,与SOC的关系不稳定,而且蓄电池内阻测量仪价格高,体积大[6]。4) 基于卡尔曼滤波器递推算法的预测方法。卡尔曼滤波法将蓄电池看作动态系统,SOC作为系统内部的一个状态量,该方法需要选择动态系统的描述方程,递推过程也涉及到复杂的矩阵求逆运算。同时,卡尔曼滤波器作为递推算法,对初值的选择十分敏感,错误的初值导致估计不断恶化,初始SOC0可以使用开路电压给定,但用于递推的其他初值并没有较好的方式确定[7]。5) 基于神经网络的预测方法。利用神经网络较强的非线性映射能力来实现蓄电池SOC的预测。该方法避免了传统方法对模型和参数的依赖,不需要外加电流和信号处理,提高了系统鲁棒性和抗干扰能力。但神经网络目前还存在过拟合、易陷入局部极值、结构设计依赖于经验等缺陷[8]。由Vapnik[9]提出的最小二乘支持向量机(LS-SVM) 是继神经网络之后机器学习领域又一重要成果,其遵循结构风险最小化准则,结构参数在训练过程中根据样本数据自动确定,不存在过拟合现象。它将标准SVM的学习问题转化为解线性方程组问题,加快了求解速度,克服了神经网络的缺陷。本文作者用最小二乘支持向量机设计HEV铅酸蓄电池SOC预测器,描述蓄电池电压、电流以及温度与其SOC之间的非线性关系。本文考虑到最小二乘支持向量机的参数选择会对预测结果产生较大的影响,首先采用模拟退火算法寻求LS-SVM参数的最佳初始值,其次分别运用贝叶斯证据框架算法[10]以及留一交叉验证算法[11]对参数进行寻优,最后在实验中比较这2种优化算法的预测精度。
1 最小二乘支持向量机回归原理
支持向量机(SVM)是数据挖掘中的一项新技术,它的结构风险最小化原则使其经验风险与置信区间之和达到最小,提高了模型的推广能力。最小二乘支持向量机是SVM的一种改进,它将传统支持向量机中的不等式约束改为等式约束,且将误差平方和损失函数作为训练集的经验损失,这样就把二次规划问题转化为线性方程组问题,提高了求解的计算速度和收敛精度[12]。
设样本为维向量,给定个样本数据,可以表示为:(1,1),…,(,)(其中为样本输入向量,为样本输出向量)。首先,用非线性映射把输入向量从原空间R映射到特征空间,在这个特征空间中构造一个最优决策函数为
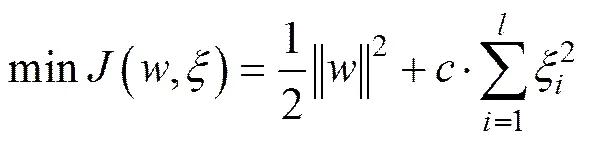

由最优解条件:
可得到
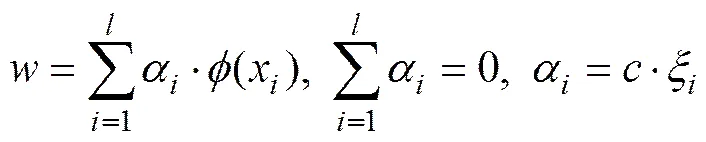
2 LS-SVM预测模型的参数优化
在给定训练样本集和确定使用 RBF 核函数后,LS-SVM 模型还需要确定正则化参数和核参数。的作用是调节LS-SVM置信范围和经验风险的比例,取其折中以使其泛化能力最好。又称为核宽度,它反映训练样本数据的分布特性,确定局部领域的宽度,较大的意味着较低的方差。所以,这2个参数在很大程度上决定了 LS-SVM 的学习能力 和泛化能力。寻找最优参数将会极大提高LS-SVM的性能。
2.1 模拟退火算法
模拟退火算法是模拟金属退火的一种计算方法,统计力学表明,在状态下,原子能量的概率分布在温度满足Boltzman方程:
2.2 贝叶斯证据框架优化算法
贝叶斯证据框架下的基本思想是最大化参数分布的后验,而最佳参数值或模型是在参数分布后验最大化的情况下得到的。贝叶斯推断分为3级:第1级确定和;第2级推断预测正则化系数;第3极推断核参数。整个推断的基础就是贝叶斯准则:
在贝叶斯第一准则下,标准支持向量机预测算法可解释为对自由参数的贝叶斯推断。利用最大化参数的后验,即可得到参数的最佳值,参数的后验式为
其中:为数据空间;为模型空间[14]。
在贝叶斯第二准则下,利用贝叶斯参数推断模型对最小二乘支持向量机正则化参数进行推断。利用最大化参数的后验,即可得到参数的最佳值。参数的后验式为
在贝叶斯第三准则下,支持向量机预测算法的最优核参数选择可以看作为贝叶斯证据框架理论对核参数的推断预测即模型比较的过程。利用最大化模型的后验,即可得到最小二乘支持向量机核参数的最佳值。模型的后验式为
2.3 留一交叉验证优化算法
参数优化通常通过最小化均方误差(MSE)的预测来实现,在参数空间内寻优,找到均方误差最小的参数取值。均方误差的公式为
其中:y为实际值;为估计值;为测试样本个数,=1, 2, …,。
常用的推广误差预测方法为交叉验证优化算法,交叉验证法一般采用均方误差来预测,因为它能充分利用样本集中所有数据进行训练和验证,在有限样本容量前提下,尽量减小“过拟合”问题。而且,交叉验证法可以在样本固定的前提下得到比较稳定的误差指标,尽量避免因随机选择训练集和测试集导致测试误差的随机变化。交叉验证形式分为Holdout交叉验证、K折交叉验证和留一交叉验证,由于蓄电池SOC属于小样本预测,而留一交叉验证对小样本预测优化有着独特的优势,因此,这里选用留一交叉验证优化算法[15]。
假设数据集中有个样本,留一交叉验证的基本思想就是讲每个样本单独作为1次测试集,剩余−1个样本则作为训练集,这样每一回合中几乎所有的样本皆用于训练模型,因此,最接近母体样本的分布。另外,在实验过程中,没有随机因素会影响实验数据,确保实验过程是可以被复制的。
2.4 预测模型实现流程
1) 确定蓄电池SOC预测建模所需的输入、输出变量;
2) 采集输入、输出样本数据,归一化处理后,建立用于训练和测试LS-SVM模型的输入输出样本集;
3) 采用模拟退火算法确定LS-SVM预测模型的参数初始值,也即和的初始值;
4) 初始值确定后,利用训练样本集训练LS-SVM,建立SOC预测模型;
5) 分别基于贝叶斯证据框架和留一交叉验证优化算法对模型参数进行寻优;
7) 用建立的模型进行预测和误差分析。
3 仿真实验
3.1 输入输出变量确定
蓄电池的外部特性参数有电压、电流、温度和内阻等。由于蓄电池内阻受蓄电池温度、静置时间和充放电初始状态等因素的影响,与SOC的关系不稳定,而且蓄电池内阻测量仪价格高、体积大,因此,选用电压、电流和温度这3个外部特性参数来对蓄电池SOC进行预测。
3.2 样本数据采集
采用12V/24AH的HEV用VRLA蓄电池,在室温和恒定负载条件下,获得蓄电池实时放电电压、放电电流和温度,作为LS-SVM的输入和预测集。考虑到最低电压限制,所以在放电实验时,放电电压不低于10.5 V[18]。蓄电池放电过程中各个时刻的SOC数值是通过计算蓄电池放电到截止电压时所释放的总电量,然后用此总电量作为基准计算得到[19]。为简化试验,实际试验中没有考虑回馈制动产生的能量,即蓄电池一直处于放电状态。同时,蓄电池每个面上都放置了温度探头,最终用于分析的表面温度数据是所有探头数值的平均值。图1所示为实测电压、实测电流、实测温度和蓄电池SOC的真实值随时间变化的曲线。重复2次放电试验,共计960 min,每次试验取72组电压、电流和温度数据,共144组,576个数据,其中第1次放电数据作为训练集,第2次放电数据作为测试集。
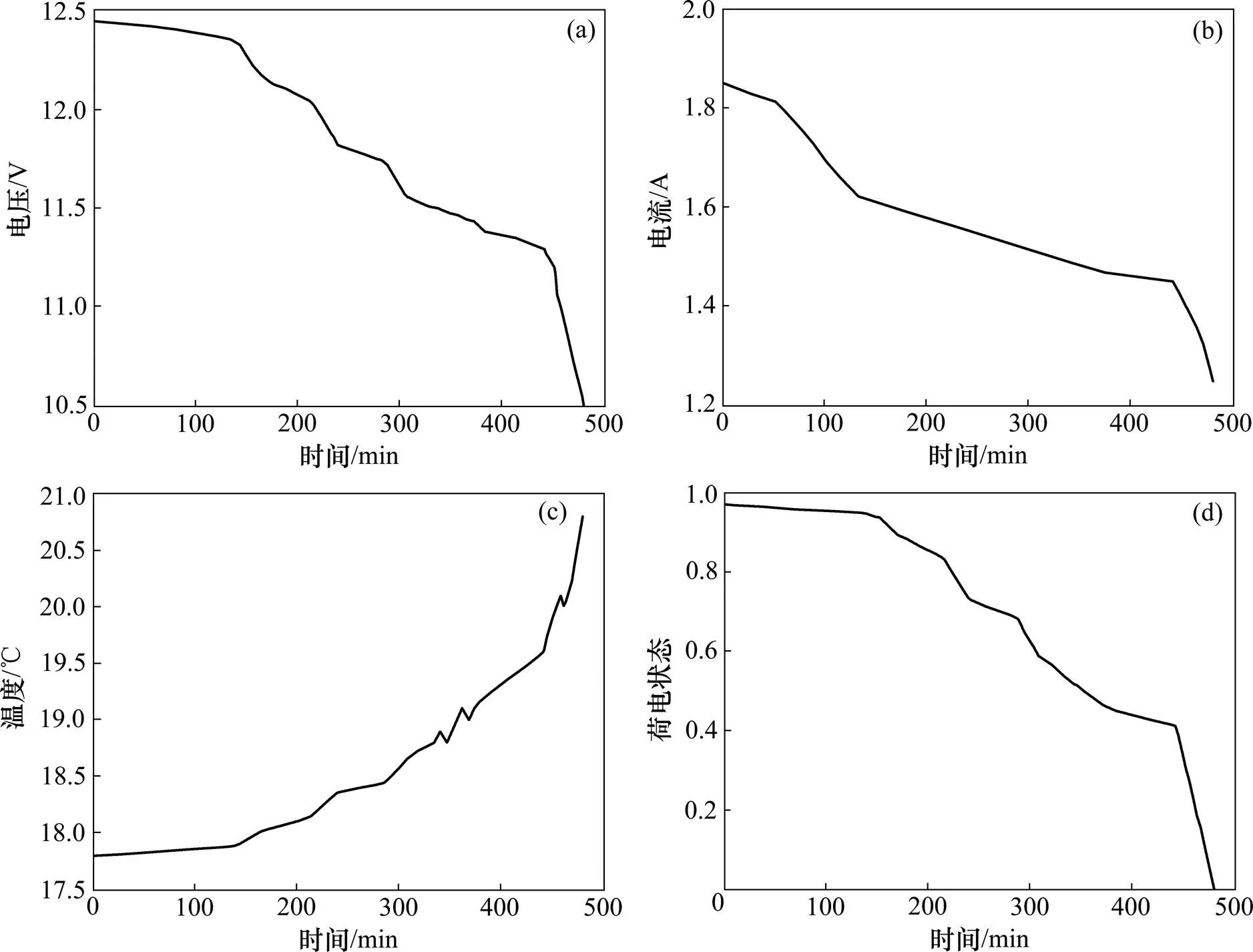
(a) 电压;(b) 电流;(c) 温度;(d) 荷电状态
图1 实测电压、电流、温度和SOC真实值
Fig. 1 Measured voltage, current, temperature and true value of SOC
3.3 仿真分析
在MATLAB 7平台上对基于参数优化的最小二乘支持向量机HEV阀控铅酸蓄电池SOC进行预测,需要注意的是仿真中模拟退火算法的冷却时间为1 s。2种优化算法的寻优路径均采用单纯形法,其基本思想是:先找出1个基本可行解,对它进行鉴别,看是否为最优解,若不是,则按照一定法则转换到另一改进的基本可行解,再鉴别;若仍不是,则再转换,按此重复进行。表1所示为2种算法的优化结果,预测结果分别如图2和图3所示。

表1 参数优化结果
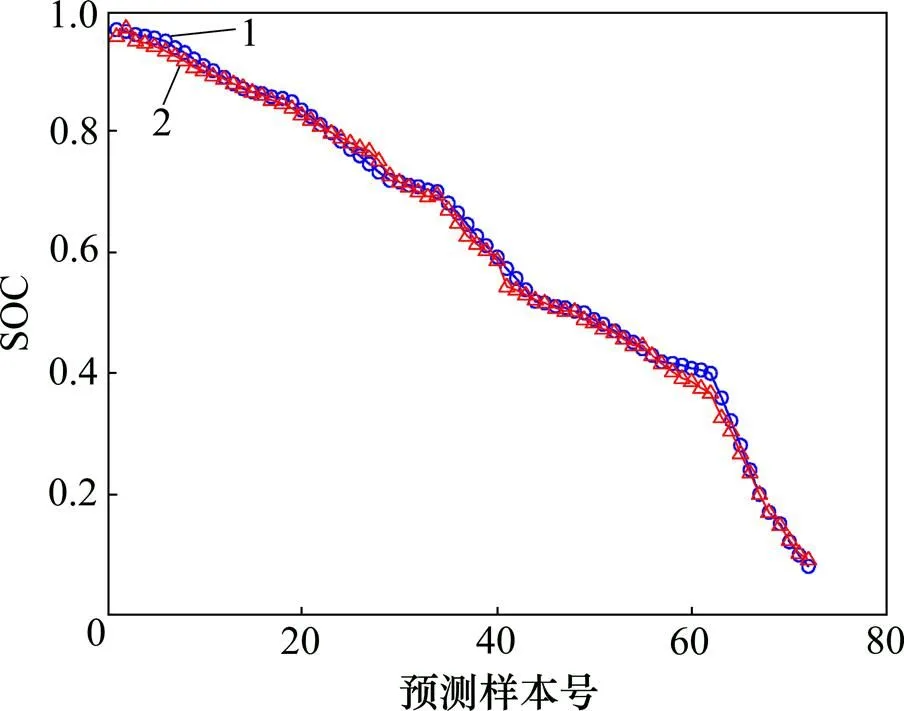
1—真实数据;2—回归预测数据
图2 基于贝叶斯证据框架优化的预测结果
Fig. 2 Prediction results based on Bayesian evidence framework optimization

1—真实数据;2—回归预测数据
图3 基于留一交叉验证优化的预测结果
Fig. 3 Prediction results based on Leave-one-out cross-validation optimization
从表1和图2、图3可见:2种算法在设定参数下均有较好的收敛特性,基于留一交叉验证优化算法的预测曲线相比于贝叶斯证据框架优化,其回归预测数据与真实数据咬合得更加紧密,同时优化速度明显提高。
3.4 模型评价
为了进一步说明贝叶斯证据框架优化算法和留一交叉验证优化算法所建预测模型的优劣,采用预测值和真实值的均方误差(MSE)、绝对误差(AE)和相对误差(RE)作为评价指标来评价模型,均方误差主要评价预测模型的整体性能,而绝对误差和相对误差主要衡量预测模型的局部性能。AE和RE的定义为
其中:y为实际值;为估计值;为测试样本个数;=1, 2, …,。
基于上述评价指标,比较贝叶斯证据框架和留一交叉验证算法所建LS-SVM模型的拟合和预测能力,2种模型的MSE,AE和RE比较结果分别见表2和图4~7。
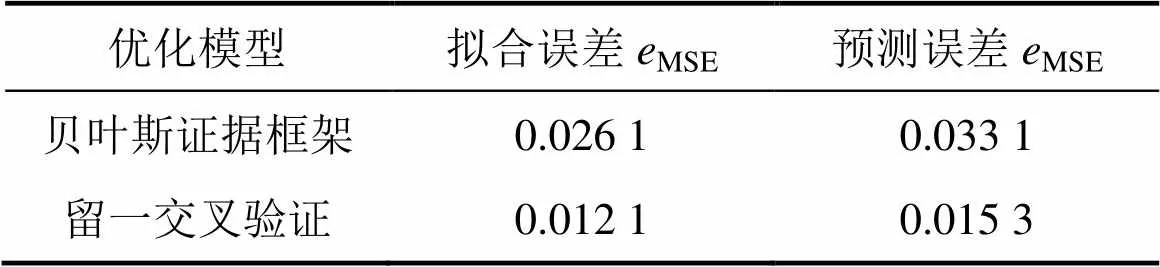
表2 2种优化模型拟合和预测能力比较
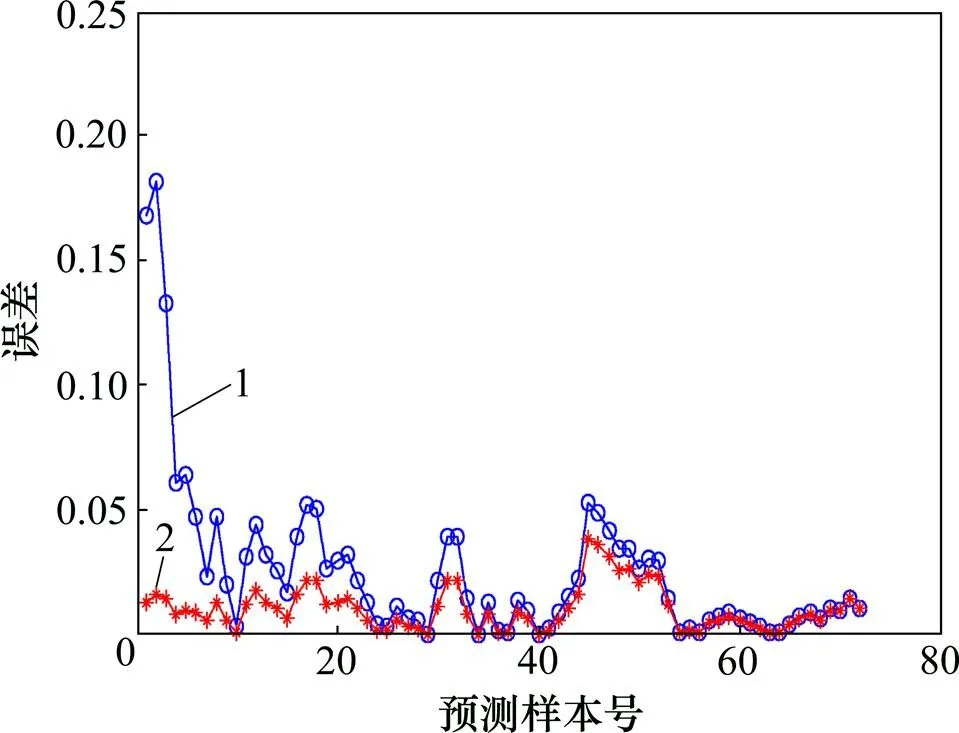
1—相对误差;2—绝对误差
图4 基于贝叶斯证据框架优化的拟合误差
Fig. 4 Fitting errors based on Bayesian evidence framework optimization
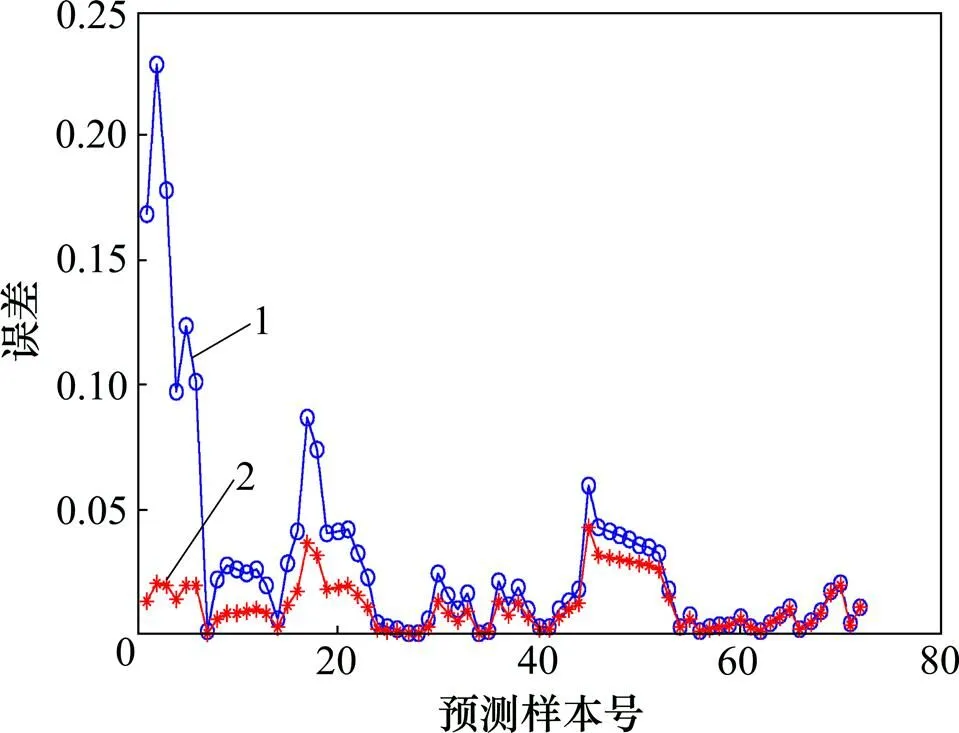
1—相对误差;2—绝对误差
图5 基于贝叶斯证据框架优化的预测误差
Fig. 5 Prediction errors based on Bayesian evidence framework optimization

1—相对误差;2—绝对误差
图6 基于留一交叉验证优化的拟合误差
Fig. 6 Fitting errors based on Leave-one-out cross-validation optimization
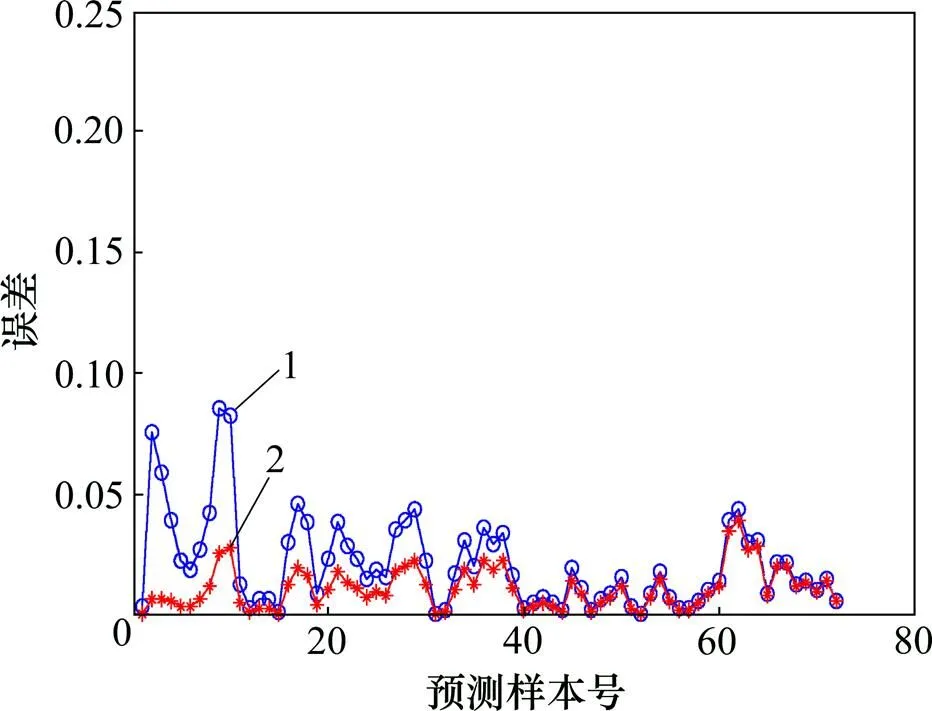
1—相对误差;2—绝对误差
图7 基于留一交叉验证优化的预测误差
Fig. 7 Prediction errors based on Leave-one-out cross-validation optimization
从表 2 可以看出:留一交叉验证优化模型的拟合误差和预测误差约为贝叶斯证据框架优化模型的1/2。比较图4~7可以发现:2种优化算法的拟合绝对误差和预测绝对误差都较低,在0~5%之间来回浮动;贝叶斯证据框架优化模型的拟合相对误差和预测相对误差起始波动较大,误差约为20%,而且在拟合和预测过程中有相对误差高于5%的盲点出现。留一交叉验证优化模型的拟合相对误差和预测相对误差稳定后基本位于5%以内,且分布更加密集。由此可见留一交叉验证优化LS-SVM 建模方法能够有效改善模型的拟合能力并提高预测精度。
4 结论
1) 基于参数优化的LS-SVM可用于对HEV铅酸蓄电池SOC进行准确预测。
2) 模拟退火算法对寻找最佳的LS-SVM参数初始值有很好的效果,减少迭代次数和运行时间。
3) 基于留一交叉验证优化的最小二乘支持向量机SOC预测模型的预测精度比贝叶斯证据框架优化的预测模型预测精度高。
[1] Ng K S,Moo C S,Chen Y P,et al.Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries[J]. Applied Energy, 2009, 86(9): 1506−1511.
[2] 雷肖, 陈清泉, 刘开培, 等. 电动车电池SOC估计的径向基函数神经网络方法[J]. 电工技术学报, 2008, 23(5): 81−87.
LEI Xiao, CHEN C C, LIU Kaipei, et al. Battery state of charge estimation based on neural-network for electric vehicles[J]. Transactions of China Electrotechnical Society, 2008, 23(5): 81−87
[3] 戴海峰, 孙泽昌, 魏学哲. 利用双卡尔曼滤波算法估计电动汽车用锂离子动力电池的内部状态[J]. 机械工程学报, 2009, 45(6): 95−101,
DAI Haifeng, SUN Zechang, WEI Xuezhe. Estimation of internal states of power lithium-ion batteries used on electric vehicles by dual extended Kalman filter[J]. Journal of Mechanical Engineering, 2009, 45(6): 95−101.
[4] Ranjbar A H, Banaei A, Khoobroo A. Online estimation of state of charge in Li-ion batteries using impulse response concept[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 360−367.
[5] Alvarez Anton J C, Garcia Nieto P J, Blanco Viejo C, et al. Support vector machines used to estimate the battery state of charge[J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5919−5926.
[6] van Bree P J, Veltman A, Hendrix W H A, et al. Prediction of battery behavior subject to high-rate partial state of charge[J]. IEEE Transactions on Vehicular Technology, 2009, 58(2): 588−595.
[7] Lee D T, Shiah S J, Lee C M, et al. State of charge estimation for electric scooters by using learning mechanisms[J]. IEEE Transactions on Vehicular Technology, 2007, 56(2): 544−556.
[8] 朱志莹, 孙玉坤. 群优化支持向量机的磁轴承转子位移预测模型[J]. 中国电机工程学报, 2012, 32(33): 118−123.
ZHU Zhiying, SUN Yukun. Predictive modeling of rotor displacement for magnetic bearing using particle swarm optimized-least squares support vector machines[J]. Proceedings of the CSEE, 2012, 32(33): 118−123.
[9] Vapnik V N. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1999: 181−217.
[10] 阎威武, 常俊林, 邵惠鹤. 一种贝叶斯证据框架下支持向量机建模方法的研究[J]. 控制与决策, 2004, 19(5): 525−533.
YAN Weiwu, CHANG Junlin, SHAO Huihe. Modeling method based on support vector machines with in the Bayesian evidence framework[J]. Control and Decision, 2004, 19(5): 525−533.
[11] 李锋, 汤宝平, 章国稳. 基于舍一交叉验证最小二乘支持向量机的故障诊断模型[J]. 振动与冲击, 2010, 29(9): 170−174.
LI Feng, TANG Baoping, ZHANG Guowen. Fault diagnosis model based on least square support vector machine optimized by leave-one outcross-validation[J]. Journal of Vibration and Shock, 2010, 29(9): 170−174.
[12] 陈刚, 闫飞, 龚啸, 等. 基于参数优化的最小二乘支持向量机状态估计方法[J]. 电力系统保护与控制, 2011, 39(19): 83−88.
CHEN Gang, YAN Fei, GONG Xiao, et al. State estimate based on parameter-optimized least square support vector machines[J]. Power System Protection and Control, 2011, 39(19): 83−88.
[13] 胡山鹰, 陈丙珍, 何小荣. 模拟退火法用于连续变量问题全局优化初探[J]. 计算机与应用化学, 1996, 16(1): 7−13.
HU Shanying, CHEN Bingzhen, HE Xiaorong. A simulated annealing method for global optimization on the continuous variable problems[J]. Computers and Applied Chemistry, 1996, 16(1): 7−13.
[14] 李方方, 赵英凯. 贝叶斯框架下的LSSVM和贝叶斯网络及其应用[J]. 计算机工程与设计, 2007, 28(15): 3647−3649.
LI Fangfang, ZHAO Yingkai. LS-SVM algorithm of Bayesian framework and Bayesian regularization network and their applications[J]. Computer Engineering and Design, 2007, 28(15): 3647−3649.
[15] 于化龙, 倪军, 徐森. 基于留一交叉验证的类不平衡危害预评估策略[J]. 小型微型计算机系统, 2012, 10(10): 2287−2292.
YU Hualong, NI Jun, XU Seng. Pre-evaluation strategy of harmfulness caused by class imbalance based on leave-one-out cross-validation[J]. Journal of Chinese Computer System, 2012, 10(10): 2287−2292.
SOC prediction of VRLA battery for HEV based on parameter-optimized least square support vector machines
WANG Qi1, 2, SUN Yukun2, 3, HUANG Yonghong1, 2
(1. School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China;2. Key Laboratory of Facility Agriculture Measurement and Control Technology and Equipment of Machinery Industry, Jiangsu University, Zhenjiang 212013, China;3. School of Electrical Power Engineering, Nanjing Institute of Technology, Nanjing 211167, China)
Least square support vector machines (LS-SVM) method was used to predict valve regulated lead acid (VRLA) battery’s state of charge (SOC) for hybrid electric vehicles (HEV). Considering that parameter selection of support vector machines exerted a major influence on SOC predict, a SOC prediction algorithm was presented on the basis of parameter-optimized least square support vector machines. Firstly, in the training process of nonlinear regression predicted model, simulate anneal arithmetic was adopted to determine starting values of the LS-SVM algorithm for better reflecting the complexity of the predicted model and thus increased the predicted accuracy. Secondly, owing to that the predicted model maybe produces big errors, Bayesian evidence framework (BEF) and leave-one-out cross-validation (LOOCV) optimization methods were appended to enhance robustness of the predicted model by means of analyzing characteristic of kernel parameter. The results indicate that the leave-one-out cross-validation optimization method possessed higher predicted accuracy and effectiveness.
battery; state of charge (SOC); least square support vector machines (LS-SVM); parameter-optimized; prediction
TP912
A
1672−7207(2015)01−0113−07
2014−02−26;
2014−04−16
国家自然科学基金资助项目(61074019,51377074);江苏高校优势学科建设工程资助项目(苏政办发[2011] 6号);镇江市工业科技支撑项目(GY2010005);江苏省研究生创新计划项目(CXZZ13_0683) (Projects(61074019, 51377074) supported by the National Natural Science Foundation of China; Project([2011] 6) supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions; Project(GY2010005) supported by Industrial Science and Technology of Zhenjiang; Project(CXZZ13_0683) supported by Graduate Innovation of Jiangsu Province)
王琪,博士研究生,从事混合动力汽车复合电源及能量管理研究;E-mail: wangqitz@163.com
10.11817/j.issn.1672−7207.2015.01.016
(编辑 杨幼平)

